Integrales de superficie de campos vectoriales: flujo

El último concepto a definir es el de integral de un campo vectorial sobre una superficie, que está relacionado con el concepto físico de flujo a través de una superficie.

Integral de superficie o flujo:

Dada una superficie \(S\) y un campo vectorial \(\vec{F}(x,y,z)\) definido sobre \(S\), se define la integral de superficie de \(\vec{F}\) sobre \(S\), o flujo de \(\vec{F}\) sobre \(S\), como:

\[Flujo=\iint_S \vec{F}\cdot d\vec{s}=\iint_S \vec{F}\cdot\vec{n}\,ds\]

siendo \(\vec{n}\) el vector normal unitario, es decir, perpendicular al plano tangente en cada punto de la superficie, y \(ds\) un elemento diferencial de área sobre la superficie.

El producto escalar \(\vec{F}\cdot\vec{n}\) permite obtener la componente del campo vectorial en la dirección perpendicular a la superficie.

Físicamente, si el campo vectorial se interpreta como un campo de velocidades de un fluido, la integral de superficie puede verse como la cantidad de fluido que atraviesa la superficie por unidad de tiempo.

---

Ejemplo:

Dado el campo vectorial \(\vec{F}=x\vec{i}+y\vec{j}+z\vec{k}\), se desea calcular el flujo que atraviesa la esfera de radio \(R\) y centrada en el origen.

import matplotlib.pyplot as plt
import numpy as np

fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
phi, theta = np.meshgrid(np.linspace(0, np.pi, 50), np.linspace(0, 2*np.pi, 50))
R = 1
x, y, z = R*np.sin(phi)*np.cos(theta), R*np.sin(phi)*np.sin(theta), R*np.cos(phi)
ax.plot_surface(x, y, z, cmap='viridis')
xx, yy, zz = np.meshgrid(np.linspace(-1,1,5), np.linspace(-1,1,5), np.linspace(-1,1,5))
ax.quiver(xx, yy, zz, xx, yy, zz, length=0.25)
ax.set_box_aspect([1, 1, 1])
plt.show()

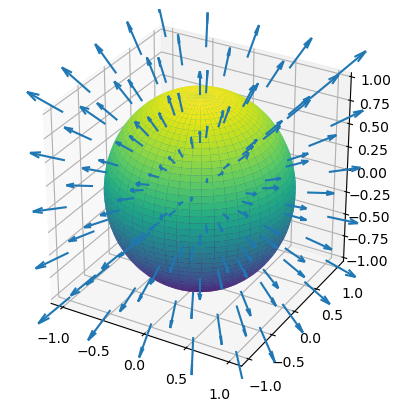
El vector unitario normal a la superficie de la esfera sería

\[\vec{n}=\frac{1}{R}(x,y,z)\]

ya que en los puntos de la superficie de la esfera se verificaría la condición \(x^2+y^2+z^2=R^2\). En este caso concreto, el vector normal es paralelo al correspondiente vector del campo \(\vec{F}\), y por tanto:

\[\vec{F}\cdot\vec{n}=\|\vec{F}(x,y,z)\|\,\|\vec{n}(x,y,z)\|=R\]

ya que \(\vec{n}\) es un vector unitario y \(\vec{F}\) sobre la superficie de la esfera tiene norma \(R\).

En definitiva, el flujo total que atraviesa la esfera es:

\[Flujo=\iint_S \vec{F}\cdot d\vec{s}= \iint_S \vec{F}\cdot\vec{n}\,ds=R\iint_S ds=R\,area(S)=4\pi R^3\]

---

Normalmente las superficies vienen dadas por parametrizaciones, por lo que se requiere obtener una fórmula que permita evaluar el flujo a partir de la parametrización de la superficie.

Dado un conjunto conexo \(\Omega\subseteq R^2\) y una superficie parametrizada \(S\) definida por

\[\begin{split}\begin{array}{rl} \vec{s}:\Omega &\longrightarrow R^3\\ (u,v) &\longrightarrow \vec{s}(u,v)=(s_1(u,v),s_2(u,v),s_3(u,v)) \end{array}\end{split}\]

con \((u,v)\in\Omega\), los dos vectores normales unitarios son:

\[\vec{n}(\vec{s}(u,v))=\frac{\frac{\partial \vec{s}}{\partial u}(u,v)\times \frac{\partial \vec{s}}{\partial v}(u,v)} {\left\| \frac{\partial \vec{s}}{\partial u}(u,v)\times \frac{\partial \vec{s}}{\partial v}(u,v) \right\|} \]

\[-\vec{n}(\vec{s}(u,v))=-\frac{\frac{\partial \vec{s}}{\partial u}(u,v)\times \frac{\partial \vec{s}}{\partial v}(u,v)} {\left\| \frac{\partial \vec{s}}{\partial u}(u,v)\times \frac{\partial \vec{s}}{\partial v}(u,v) \right\|} \]

Eligiendo el primer vector como vector normal, puede comprobarse que el producto del vector normal por el elemento diferencial de área sería:

\[\vec{n}\,ds =\left( \frac{\partial \vec{s}}{\partial u}(u,v)\times \frac{\partial \vec{s}}{\partial v}(u,v) \right)du\,dv \]

y por tanto, la integral de superficie o flujo de \(\vec{F}\) sobre \(S\) se calcularía mediante la integral:

\[Flujo=\iint_\Omega \vec{F}(\vec{s}(u,v))\cdot \left(\frac{\partial \vec{s}}{\partial u}(u,v)\times \frac{\partial \vec{s}}{\partial v}(u,v)\right) \,du\,dv \]

Se podría comprobar que la integral anterior tendría el mismo valor para diferentes parametrizaciones de la superficie siempre que consideren la misma orientación. El flujo es una integral orientada, lo que significa que si se cambia la orientación de la superficie el valor del flujo cambia de signo.

De nuevo, la integral de superficie cumple las propiedades de linealidad, aditividad en la superficie de integración y acotación.

---

Ejemplo:

Dado el campo vectorial del ejemplo anterior \(\vec{F}=x\vec{i}+y\vec{j}+z\vec{k}\), para calcular el flujo que atraviesa la esfera de radio \(R\) y centrada en el origen con ayuda de Python, se podría seguir el procedimiento siguiente:

• Determinar la parametrización de la superficie:

import sympy as sp
u,v,R = sp.symbols('u,v,R')
sx = R*sp.sin(u)*sp.cos(v)
sy = R*sp.sin(u)*sp.sin(v)
sz = R*sp.cos(u)

• Calcular el vector normal \(\frac{\partial \vec{s}}{\partial u}(u,v)\times \frac{\partial \vec{s}}{\partial v}(u,v)\) definiendo previamente un sistema de coordenadas

import sympy.vector as vec
S = vec.CoordSys3D('')
v1 = sp.diff(sx,u)*S.i + sp.diff(sy,u)*S.j + sp.diff(sz,u)*S.k
v2 = sp.diff(sx,v)*S.i + sp.diff(sy,v)*S.j + sp.diff(sz,v)*S.k
normal = v1.cross(v2)
normal.simplify()

\[\displaystyle (R^{2} \sin^{2}{\left(u \right)} \cos{\left(v \right)})\mathbf{\hat{i}_{}} + (R^{2} \sin^{2}{\left(u \right)} \sin{\left(v \right)})\mathbf{\hat{j}_{}} + (\frac{R^{2} \sin{\left(2 u \right)}}{2})\mathbf{\hat{k}_{}}\]

• Identificar la orientación que determina el vector normal. En este caso, el vector es la normal saliente, es decir, del interior de la esfera hacia afuera.

• Definir el campo vectorial sobre el sistema de coordenadas evaluado sobre la superficie

F = sx*S.i + sy*S.j + sz*S.k

• Calcular la integral doble del producto escalar del vector de campo por el vector normal, en el dominio de variación de los parámetros de la superficie

flujo = sp.integrate(F.dot(normal), (u,0,sp.pi), (v,0,2*sp.pi))
flujo

\[\displaystyle 4 \pi R^{3}\]

El hecho de que el flujo tenga signo positivo significa que es un flujo en la mismo sentido que el vector normal, es decir, un flujo de salida de la esfera.

Hay otra opción más directa para calcular flujos, se trata de la función vector_integrate() del paquete Vector del módulo SymPy. Esta función es la misma que se utiliza para calcular integrales de línea, pero es capaz de indetificar si se le aporta un campo escalar o vectorial, y una curva o superficie.

El flujo sobre la esfera del ejemplo se calcularía de la siguiente manera:

esfera = vec.ParametricRegion((R*sp.sin(u)*sp.cos(v), R*sp.sin(u)*sp.sin(v), R*sp.cos(u)), 
                              (u,0,sp.pi), (v,0,2*sp.pi))
F = S.x*S.i + S.y*S.j + S.z*S.k
vec.vector_integrate(F, esfera)

\[\displaystyle 4 \pi R^{3}\]

---

Ejemplo:

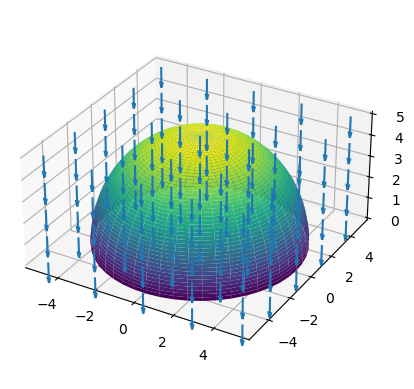
Se desea calcular el flujo del campo constante \(\vec{F}=-2\vec{k}\) sobre la semiesfera de radio 5, centrada en el origen y con \(z\geq 0\)

fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
phi, theta = np.meshgrid(np.linspace(0, np.pi/2), np.linspace(0, 2*np.pi))
x, y, z = 5*np.sin(phi)*np.cos(theta), 5*np.sin(phi)*np.sin(theta), 5*np.cos(phi)
ax.plot_surface(x, y, z, cmap='viridis')
xx, yy, zz = np.meshgrid(np.linspace(-5,5,5),np.linspace(-5,5,5),np.linspace(0,5,5))
ax.quiver(xx, yy, zz, 0, 0, -2, length=0.5)
ax.set_box_aspect([1, 1, 0.5])
plt.show()

phi, theta = sp.symbols("phi theta")
semiesfera = vec.ParametricRegion((5*sp.sin(phi)*sp.cos(theta), 5*sp.sin(phi)*sp.sin(theta), 5*sp.cos(phi)),
                                  (phi, 0, sp.pi/2), (theta, 0, 2*sp.pi))
flujo = vec.vector_integrate(-2*S.k, semiesfera)
flujo

\[\displaystyle - 50 \pi\]

En este caso el flujo es negativo, y por tanto contrario al sentido del vector normal. Como se vió en el gráfico del campo, el flujo es hacia el interior de la esfera.

---

Ejemplo:

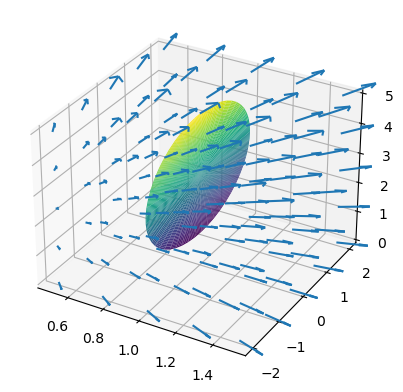
se desea calcular el flujo del campo \(\vec{F}(x,y,z)=x\vec{i}+y\vec{j}+z\vec{k}\) sobre un disco circular de radio 2 situado verticalmente en el plano \(x=1\) y con el centro en el punto \((1,0,3)\)

En primer lugar podemos visualizar en un mismo gráfico la superficie y el campo, para observar el sentido del flujo que atraviesa la superficie

fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
u,v = np.meshgrid(np.linspace(0, 2), np.linspace(0, 2*np.pi))
x,y,z = 1, u*np.cos(v), 3 + u*np.sin(v)
ax.plot_surface(x, y, z, cmap='viridis')
xx, yy, zz = np.meshgrid(np.linspace(0.5,1.5,5),np.linspace(-2,2,5),np.linspace(0,5,5))
vx, vy, vz = xx, yy, zz
ax.quiver(xx,yy,zz,vx,vy,vz, length=0.1)
plt.show()

El flujo se calcularía de la siguiente manera:

u,v = sp.symbols('u,v')
disco = vec.ParametricRegion((1, u*sp.cos(v), 3+u*sp.sin(v)), (u,0,2), (v,0,2*sp.pi))
F = S.x*S.i + S.y*S.j + S.z*S.k
flujo = vec.vector_integrate(F, disco)
flujo

\[\displaystyle 4 \pi\]

---

Como caso particular, considérese el caso de una superficie definida mediante una ecuación explícita \(z=f(x,y)\). Una parametrización podría ser:

\[\vec{s}(x,y)=(x,y,f(x,y))\;\;\mbox{ con }(x,y)\in\Omega\]

y por tanto

\[\vec{n}\,ds = \left( \left(1,0,\frac{\partial f}{\partial x}\right) \times \left(0,1,\frac{\partial f}{\partial y}\right) \right)dx\,dy = \left( -\frac{\partial f}{\partial x},-\frac{\partial f}{\partial y},1 \right)dx\,dy \]

El flujo del campo \(\vec{F}\) a través de la superficie \(z=f(x,y)\) sería entonces:

\[Flujo= \iint_\Omega \vec{F}(x,y,f(x,y))\cdot \left( -\frac{\partial f}{\partial x},-\frac{\partial f}{\partial y},1 \right)dx\,dy \]

---

Ejemplo:

Se desea calcular el flujo del campo vectorial \(\vec{F}(x,y,z)=3x\vec{i}-y\vec{j}-z\vec{k}\) a través de la porción del paraboloide \(z=9-x^2-y^2\) que se encuentra en el primer octante, considerando como orientación positiva la normal saliente.

fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
x, y = np.meshgrid(np.linspace(-3,3), np.linspace(-3,3))
z = 9-x**2-y**2
ax.plot_surface(x, y, z, cmap='viridis')
xx, yy, zz = np.meshgrid(np.linspace(-3,3,5),np.linspace(-3,3,5),np.linspace(-3,3,5))
ax.quiver(xx, yy, zz, 3*xx, -yy, -zz, length=0.1)
plt.show()

De acuerdo a la expresión que determina el flujo sobre superficies explícitas, el flujo del campo sobre la superficie sería:

\[Flujo= \iint_\Omega (3x,-y,x^2+y^2-9)\cdot(2x,2y,1) dx\,dy =\iint_\Omega (7x^2-y^2-9)dx\,dy \]

siendo \(\Omega=\{(x,y)|x^2+y^2\leq 9;\,x,y\geq 0\}\) la proyección de la superficie sobre el plano \(OXY\). Por tanto, haciendo un cambio a coordenadas polares, se obtiene

\[ Flujo = \int_0^{\pi/2}\left(\int_0^3(7r^2\cos^2\theta-r^2\sin^2\theta-9)r\, dr\right) d\theta\]

\[ = \int_0^{\pi/2}\left(\int_0^3(4r^2\cos(2\theta) + 3r^2 - 9)r\, dr\right) d\theta \]

\[ = \int_0^{\pi/2}(81\cos(2\theta)+81/4)d\theta = \frac{81\pi}{8} \]

Se puede comprobar fácilmente esos cálculos con ayuda de Python y parametrizando la superficie con:

\[\vec{s}(u,v)=(u\cos v,u\sin v, 9-u^2)\mbox{ con }u\in[0,3], v\in[0,2\pi]\]

u,v = sp.symbols("u,v")
F = 3*S.x*S.i - S.y*S.j - S.z*S.k
paraboloide = vec.ParametricRegion((u*sp.cos(v), u*sp.sin(v), 9-u**2),
                                   (u, 0, 3), (v, 0, 2*sp.pi))
flujo = vec.vector_integrate(F, paraboloide)
flujo

\[\displaystyle \frac{81 \pi}{2}\]

Ejercicios propuestos

• Hallar el flujo del campo vectorial \(\vec{F}=y\vec{i}+x\vec{j}+z\vec{k}\) a través de la superficie del paraboloide \(z=1-x^2-y^2\) que se encuentra por encima del plano \(OXY\).

• Hallar el flujo del campo vectorial \(\vec{F}=y^2\vec{i}-y\vec{j}+xyz\vec{k}\) a través de la superficie lateral del cilindro \(x^2+y^2=4\) con \(0\leq z\leq 4\).

• Calcular el flujo del campo \(\vec{F}=xy\vec{i}+z^2\vec{j}+xz\vec{k}\) sobre la superficie triangular determinada por los puntos \((2,0,0)\), \((0,3,0)\) y \((0,0,1)\).

• Calcula el flujo del campo \(\vec{F}=\sqrt{y}\vec{j}\) sobre la superficie \(S=\left\{ (x,y,z)|\,x^2+z^2=y;\;\;0\leq y\leq 1 \right\}\).

• El flujo de calor viene determinado por el campo vectorial \(\vec{F}=-k\nabla T\) donde \(k>0\) representa la conductividad del medio y \(T\) la temperatura en cada punto del espacio. Supongamos que en una esfera centrada en el origen y de radio 1 la temperatura de un punto es proporcional al cuadrado de la distancia de dicho punto al centro de la esfera. Calcular el flujo total de calor que atraviesa la esfera.