Sistemas lineales de ecuaciones diferenciales de primer orden#

Hasta ahora se han considerado ecuaciones con una única función incógnita en una variable independiente, sin embargo, en muchas ocasiones deben considerarse simultáneamente varias ecuaciones diferenciales ordinarias con varias funciones incógnita. En esta sección se analizará un tipo especial de sistemas de ecuaciones: los sistemas lineales de ecuaciones diferenciales ordinarias de primer orden y con coeficientes constantes.

Suponiendo que \(y_1,y_2,\dots y_n\) son funciones de una variable independiente \(x\), los sistemas que se van a analizar en esta sección son de la forma:

\[\begin{split}\begin{array}{l} \frac{dy_1}{dx} = a_{11}y_1+a_{12}y_2+\dots+a_{1n}y_n+g_1(x) \\ \frac{dy_2}{dx} = a_{21}y_1+a_{22}y_2+\dots+a_{2n}y_n+g_1(x) \\ \vdots && \\ \frac{dy_n}{dx} = a_{n1}y_1+a_{n2}y_2+\dots+a_{nn}y_n+g_n(x) \end{array}\end{split}\]

que pueden ser también expresados en forma matricial:

\[Y'=AY+G(x)\]

donde

\[\begin{split}Y= \left( \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \\ \end{array} \right),\;\;\;\;\;\; A=\left( \begin{array}{cccc} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \dots & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nn} \\ \end{array} \right),\;\;\;\;\;\; G(x)= \left( \begin{array}{c} g_1(x) \\ g_2(x) \\ \vdots \\ g_n(x) \\ \end{array} \right) \end{split}\]

Cuando \(G(x)=\vec{0}\) el sistema se dice homogéneo.

Al igual que ocurría con las ecuaciones diferenciales lineales de orden superior, la solución general de un sistema lineal de ecuaciones diferenciales va a ser expresada como:

\[Y=Y_h+Y_p\]

donde \(Y_h\) es la solución general del sistema homogéneo asociado e \(Y_p\) una solución particular del sistema completo.

Solución general de un sistema homogéneo#

Al igual que ocurría con las ecuaciones lineales, el objetivo es encontrar un sistema fundamental de soluciones, de manera que la solución general del sistema será la combinación lineal de las soluciones del sistema fundamental.

Dado un sistema homogéneo \(Y'=AY\), si se desea buscar soluciones del sistema homogéneo de la forma

\[\begin{split}Y=\left( \begin{array}{c} k_1 \\ k_2 \\ \vdots \\ k_n \\ \end{array} \right)e^{\lambda x}=Ke^{\lambda x}\end{split}\]

se tendría \(Y'=K\lambda e^{\lambda x}\), por lo que se debería cumplir

\[K\lambda e^{\lambda x} = AK e^{\lambda x}\]

o equivalentemente

\[(A-\lambda I)K=0\]

lo que significa que \(\lambda\) sería un autovalor y \(K\) un autovector de la matriz de coeficientes \(A\).

Dada una matriz cuadrada \(A=(a_{ij})_{n\times n}\), los autovalores o valores propios son aquellos números (reales o complejos) \(\lambda\) para los cuáles existe al menos un vector no nulo \(\vec{v}\) tal que

\[A\vec{v}=\lambda\vec{v}\]

o lo que es lo mismo

\[(A-\lambda I)\vec{v}=\vec{0}\]

En este caso el vector \(\vec{v}\) se dice que es un autovector asociado al autovalor \(\lambda\).

Desde un punto de vista práctico los autovalores corresponden con las raíces del polinomio característico de la matriz, es decir, la solución de la ecuación

\[\begin{split}|A-\lambda I|= \left| \begin{array}{cccc} a_{11}-\lambda & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22}-\lambda & \dots & a_{2n} \\ \vdots & \vdots & \dots & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nn}-\lambda \\ \end{array} \right|=0\end{split}\]

y los autovectores asociados a un autovalor \(\lambda\) son las soluciones del sistema de ecuaciones

\[A\vec{v}=\lambda\vec{v} \Rightarrow (A-\lambda I)\vec{v}=\vec{0}\]

Volviendo al problema de encontrar un sistema fundamental de soluciones de un sistema lineal homogéneo de ecuaciones diferenciales, se pueden dar distintas situaciones:

  • La matriz de coeficientes \(A\) del sistema tiene \(n\) autovalores reales y diferentes.

  • La matriz \(A\) tiene autovalores reales pero alguno es múltiple.

  • La matriz \(A\) tiene autovalores complejos simples o múltiples, en este caso siempre irían por parejas, un autovalor y su conjugado.

El caso más sencillo es el primero, cuando todos los autovalores son reales y simples. Si \(\lambda_1,\lambda_2,\dots,\lambda_n\in R\) son los autovalores y \(\vec{v}_1,\vec{v}_2,\dots,\vec{v}_n\) son autovectores de los respectivos autovalores, entonces el conjunto

\[\{\vec{v}_1e^{\lambda_1 x},\vec{v}_2e^{\lambda_2 x},\dots,\vec{v}_ne^{\lambda_n x}\}\]

constituye un sistema fundamental de soluciones del sistema \(Y'=AY\), y por tanto la solución general es:

\[Y=c_1\vec{v}_1e^{\lambda_1 x}+c_2\vec{v}_2e^{\lambda_2 x}+\dots+c_n\vec{v}_ne^{\lambda_n x}\]

donde \(c_1,c_2,\dots,c_n\) son \(n\) constantes arbitrarias.

Ejemplo:

Dado el sistema

\[\begin{split}\begin{array}{l} \frac{dy_1}{dx} = -4y_1+y_2+y_3\\ \frac{dy_2}{dx} = y_1+5y_2-y_3 \\ \frac{dy_n}{dx} = y_2-3y_3 \end{array}\end{split}\]

los autovalores de la matriz del sistema son las raíces del polinomio característico:

\[\begin{split}|A-\lambda I|= \left| \begin{array}{ccc} -4-\lambda & 1 & 1 \\ 1 & 5-\lambda & -1 \\ 0 & 1 & -3-\lambda \\ \end{array} \right|=-(\lambda+3)(\lambda+4)(\lambda-5)=0\end{split}\]

En este caso la matriz \(A\) tiene por tanto tres autovalores reales simples: \(\lambda_1=-3\), \(\lambda_2=-4\) y \(\lambda_3=5\). Lo que se necesita ahora es calcular un autovector para cada uno de los autovalores.

  • Los autovectores correspondientes al autovalor \(\lambda_1=-3\) se obtendrían resolviendo el sistema:

\[\begin{split}(A+3I)\left(\begin{array}{c}k_1 \\ k_2 \\ k_3\\\end{array}\right)= \left(\begin{array}{c}0 \\ 0 \\ 0\\\end{array}\right)\Rightarrow \left( \begin{array}{ccc} -1 & 1 & 1 \\ 1 & 8 & -1 \\ 0 & 1 & 0 \\ \end{array} \right) \left(\begin{array}{c}k_1 \\ k_2 \\ k_3\\\end{array}\right)= \left(\begin{array}{c}0 \\ 0 \\ 0\\\end{array}\right)\end{split}\]

Se trata de un sistema homogéneo indeterminado, con infinitas soluciones de la forma \((k,0,k)\). Como lo que se necesita es un único autovector se puede elegir

\[\begin{split}\vec{v}_1=\left(\begin{array}{c}1 \\ 0 \\ 1\\\end{array}\right)\end{split}\]

  • De la misma forma, un autovector asociado a \(\lambda_2=-4\) se obtendría resolviendo el sistema

\[\begin{split}\left( \begin{array}{ccc} 0 & 1 & 1 \\ 1 & 9 & -1 \\ 0 & 1 & 1 \\ \end{array} \right) \left(\begin{array}{c}k_1 \\ k_2 \\ k_3\\\end{array}\right)= \left(\begin{array}{c}0 \\ 0 \\ 0\\\end{array}\right)\end{split}\]

Las soluciones de este sistema son de la forma \((10k,-k,k)\), y en particular se puede tomar

\[\begin{split}\vec{v}_2=\left(\begin{array}{c}10 \\ -1 \\ 1\\\end{array}\right)\end{split}\]

  • Repitiendo el proceso para \(\lambda_3=5\), se llega al sistema

\[\begin{split}\left( \begin{array}{ccc} -9 & 1 & 1 \\ 1 & 0 & -1 \\ 0 & 1 & -8 \\ \end{array} \right) \left(\begin{array}{c}k_1 \\ k_2 \\ k_3\\\end{array}\right)= \left(\begin{array}{c}0 \\ 0 \\ 0\\\end{array}\right)\end{split}\]

Las soluciones de este sistema son de la forma \((k,8k,k)\), y se puede tomar

\[\begin{split}\vec{v}_3=\left(\begin{array}{c}1 \\ 8 \\ 1\\\end{array}\right)\end{split}\]

Calculados todos los autovalores con sus respectivos autovectores, la solución general del sistema de ecuaciones diferenciales es:

\[\begin{split} \left(\begin{array}{c}y_1 \\ y_2 \\ y_3\\\end{array}\right) = c_1\left(\begin{array}{c}1 \\ 0 \\ 1\\\end{array}\right)e^{-3x} + c_2\left(\begin{array}{c}10 \\ -1 \\ 1\\\end{array}\right)e^{-4x} + c_3\left(\begin{array}{c}1 \\ 8 \\ 1\\\end{array}\right)e^{5x} \end{split}\]

es decir

\[\begin{split}\begin{array}{l} y_1 = c_1e^{-3x}+10c_2e^{-4x}+c_3e^{5x} \\ y_2 = -c_2e^{-4x}+8c_3e^{5x} \\ y_3 = c_1e^{-3x}+c_2e^{-4x}+c_3e^{5x} \end{array}\end{split}\]

siendo \(c_1,c_2,c_3\) constantes arbitrarias.

Obviamente, con Python también es posible resolver sistemas de ecuaciones diferenciales. Se dispone de funciones que permiten realizar los diferentes pasos necesarios para la resolución (cálculo de autovalores y autovectores), pero también se puede usar la función dsolve() de SymPy para resolver sistemas.

Por ejemplo, los autovalores y autovectores de la matriz del ejemplo podrían calcularse de la siguiente manera:

import sympy as sp
A = sp.Matrix([[-4, 1, 1],
               [ 1, 5, -1],
               [ 0, 1, -3]])
A.eigenvals()

{5: 1, -3: 1, -4: 1}

A.eigenvects()

[(-4,
  1,
  [Matrix([
   [10],
   [-1],
   [ 1]])]),
 (-3,
  1,
  [Matrix([
   [1],
   [0],
   [1]])]),
 (5,
  1,
  [Matrix([
   [1],
   [8],
   [1]])])]

El uso de la función dsolve() exige definir previamente la variable independiente y las funciones incógnitas como símbolos y funciones simbólicas

x = sp.Symbol('x')
y1 = sp.Function('y1')
y2 = sp.Function('y2')
y3 = sp.Function('y3')

La resolución del sistema se obtendría de la siguiente forma:

sistema = [
    sp.Eq(y1(x).diff(x), -4*y1(x) +   y2(x) +  y3(x)),
    sp.Eq(y2(x).diff(x),    y1(x) + 5*y2(x) -  y3(x)),
    sp.Eq(y3(x).diff(x),              y2(x) - 3*y3(x))
]
sp.dsolve(sistema)

[Eq(y1(x), 10*C1*exp(-4*x) + C2*exp(-3*x) + C3*exp(5*x)),
 Eq(y2(x), -C1*exp(-4*x) + 8*C3*exp(5*x)),
 Eq(y3(x), C1*exp(-4*x) + C2*exp(-3*x) + C3*exp(5*x))]

No siempre todos los autovalores de la matriz de coeficientes son diferentes, es decir, autovalores simples. También puede ocurrir que un autovalor sea múltiple, y en ese caso se necesita que dicho autovalor aporte al sistema fundamental de soluciones tantas soluciones como su multiplicidad. Esto resulta sencillo cuando el autovalor tiene tantos autovectores linealmente independientes como dicha multiplicidad, pero esto no siempre ocurre, y se requieren estrategias más complejas para obtener más soluciones para el sistema fundamental de soluciones.

En esta sección se analiza únicamente el caso en el que se pueden obtener tantos autovectores independientes como la multiplicidad del respectivo autovalor, es decir, cuando la matriz de coeficientes es diagonalizable.

Ejemplo:

Dado el sistema dado en forma matricial

\[\begin{split}\begin{array}{l} Y'= \left( \begin{array}{ccc} 1 & -2 & 2 \\ -2 & 1 & -2 \\ 2 & -2 & 1 \\ \end{array} \right)Y \end{array}\end{split}\]

El polinomio característico es

\[\begin{split}\left| \begin{array}{ccc} 1-\lambda & -2 & 2 \\ -2 & 1-\lambda & -2 \\ 2 & -2 & 1-\lambda \\ \end{array} \right|=-(\lambda+1)^2(\lambda-5)=0\end{split}\]

cuyas raíces son \(\lambda_1=-1\) (con multiplicidad 2) y \(\lambda_2=5\)

A = sp.Matrix([[ 1, -2,  2],
               [-2,  1, -2],
               [ 2, -2,  1]])
A.eigenvals()

{5: 1, -1: 2}

A la hora de calcular los autovectores del autovalor doble, se plantea el sistema

\[\begin{split}\left( \begin{array}{ccc} 2 & -2 & 2 \\ -2 & 2 & -2 \\ 2 & -2 & 2 \\ \end{array} \right) \left(\begin{array}{c}k_1 \\ k_2 \\ k_3\\\end{array}\right)= \left(\begin{array}{c}0 \\ 0 \\ 0\\\end{array}\right)\end{split}\]

cuya solución \((k_1,k_1+k_3,k_3)\) depende de dos parámetros arbitrarios, y por tanto se pueden obtener dos autovectores linealmente independientes asociados a \(\lambda_1=-1\):

\[\begin{split}\vec{v}_1=\left(\begin{array}{c}1 \\ 1 \\ 0\\\end{array}\right),\;\;\;\;\;\; \vec{v}_2=\left(\begin{array}{c}0 \\ 1 \\ 1\\\end{array}\right)\end{split}\]

Se obtiene entonces ya dos elementos para el sistema fundamental de soluciones:

\[\begin{split}\left(\begin{array}{c}1 \\ 1 \\ 0\\\end{array}\right)e^{-x},\;\;\;\;\;\; \left(\begin{array}{c}0 \\ 1 \\ 1\\\end{array}\right)e^{-x}\end{split}\]

La tercera componente del sistema fundamental de soluciones debe salir del segundo autovalor, \(\lambda_2=5\). Se necesita para ello un único autovector, por tanto se plantea el sistema

\[\begin{split}\left( \begin{array}{ccc} -4 & -2 & 2 \\ -2 & -4 & -2 \\ 2 & -2 & -4 \\ \end{array} \right) \left(\begin{array}{c}k_1 \\ k_2 \\ k_3\\\end{array}\right)= \left(\begin{array}{c}0 \\ 0 \\ 0\\\end{array}\right)\end{split}\]

cuyas soluciones son de la forma \((k,-k,k)\). Se puede elegir

\[\begin{split}\vec{v}_3=\left(\begin{array}{c}1 \\ -1 \\ 1\\\end{array}\right)\end{split}\]

y se obtiene la tercera componente del sistema fundamental de soluciones

\[\begin{split}\left(\begin{array}{c}1 \\ -1 \\ 1\\\end{array}\right)e^{5x}\end{split}\]
A.eigenvects()

[(-1,
  2,
  [Matrix([
   [1],
   [1],
   [0]]),
   Matrix([
   [-1],
   [ 0],
   [ 1]])]),
 (5,
  1,
  [Matrix([
   [ 1],
   [-1],
   [ 1]])])]

En definitiva, la solución general del sistema de ecuaciones diferenciales es:

\[\begin{split} \left(\begin{array}{c}y_1 \\ y_2 \\ y_3\\\end{array}\right) = c_1\left(\begin{array}{c}1 \\ 1 \\ 0\\\end{array}\right)e^{-x} + c_2\left(\begin{array}{c}0 \\ 1 \\ 1\\\end{array}\right)e^{-x} + c_3\left(\begin{array}{c}1 \\ -1 \\ 1\\\end{array}\right)e^{5x} \end{split}\]

siendo \(c_1,c_2,c_3\) constantes arbitrarias.

sistema = [
    sp.Eq(y1(x).diff(x),    y1(x) - 2*y2(x) + 2*y3(x)),
    sp.Eq(y2(x).diff(x), -2*y1(x) +   y2(x) - 2*y3(x)),
    sp.Eq(y3(x).diff(x),  2*y1(x) - 2*y2(x) +   y3(x))
]
sp.dsolve(sistema)

[Eq(y1(x), C3*exp(5*x) - (C1 - C2)*exp(-x)),
 Eq(y2(x), C2*exp(-x) - C3*exp(5*x)),
 Eq(y3(x), C1*exp(-x) + C3*exp(5*x))]

Como ya se ha comentado no siempre pueden encontrarse tantos autovectores independientes como la multiplicidad del autovalor. Por ejemplo, cuando un autovalor doble únicamente tiene un autovector linealmente independiente, se trataría de buscar una segunda solución para el sistema fundamental de soluciones que responda a la siguiente estructura:

\[Y_2=\vec{v}xe^{\lambda x} + \vec{w}e^{\lambda x}\]

donde se debería cumplir

\[(A-\lambda I)\vec{v}=\vec{0}\;\;\mbox{ y }\;\;(A-\lambda I)\vec{w}=\vec{v}\]

Finalmente, también es importante aclarar cuál es el proceso de resolución del sistema cuando la matriz de coeficientes tiene autovalores complejos. En este caso cada autovalor complejo va acompañado de su conjugado y generará dos soluciones para el sistema fundamental de soluciones.

Si \(\lambda=a+bi\) es un autovalor de la matriz \(A\), y \(\vec{v}\) es una autovector complejo asociado a \(\lambda\), entonces dos soluciones independientes se obtienen de separando la parte real y la imaginaria de la expresión

\[\vec{v}e^{\lambda x}=\vec{v}e^{ax}(\cos bx + i\sin bx)\]

A continuación se ilustra el proceso con un sistema de dos ecuaciones diferenciales.

Ejemplo:

Dado el sistema

\[\begin{split}\begin{array}{l} \frac{dy_1}{dx} = 2y_1+8y_2\\ \frac{dy_2}{dx} = -y_1-2y_2 \end{array}\end{split}\]

los autovalores de la matriz del sistema son las raíces del polinomio

\[\begin{split} \left| \begin{array}{cc} 2-\lambda & 8 \\ -1 & -2-\lambda \\ \end{array} \right|=\lambda^2+4=0 \Rightarrow \lambda=\pm 2i \end{split}\]

Los autovectores asociados a \(\lambda=2i\) serían las soluciones del sistema

\[\begin{split} \left( \begin{array}{cc} 2-2i & 8 \\ -1 & -2-2i \\ \end{array} \right) \left(\begin{array}{c}k_1 \\ k_2 \\\end{array}\right)= \left(\begin{array}{c}0 \\ 0 \\\end{array}\right) \end{split}\]

de donde se saca la relación \(k_1=(-2-2i)k_2\), por lo que un autovector sería:

\[\begin{split}\vec{v}=\left(\begin{array}{c}2+2i \\ -1\\\end{array}\right)\end{split}\]

Si se desarrolla la siguiente expresión

\[\begin{split}\begin{array}{l} \left(\begin{array}{c}2+2i \\ -1\\\end{array}\right)e^{2ix} = \left(\begin{array}{c}2+2i \\ -1\\\end{array}\right)(\cos 2x + i\sin 2x) \\ = \left(\begin{array}{c} 2(\cos 2x-\sin 2x) +2i(\cos 2x+\sin 2x)\\ -\cos 2x - i\sin 2x \\ \end{array}\right) \end{array}\end{split}\]

Separando parte real y parte imaginaria se obtienen las dos soluciones del sistema fundamental de soluciones, y por tanto la solución general del sistema es:

\[\begin{split} \left(\begin{array}{c} y_1\\ y_2 \\ \end{array}\right) = c_1 \left(\begin{array}{c} 2(\cos 2x-\sin 2x) \\ -\cos 2x \\ \end{array}\right) +c_2 \left(\begin{array}{c} 2(\cos 2x+\sin 2x)\\- \sin 2x \\ \end{array}\right) \end{split}\]

siendo \(c_1,c_2\) dos constantes arbitrarias.

A = sp.Matrix([[ 2,  8],
               [-1, -2]])
A.eigenvects()

[(-2*I,
  1,
  [Matrix([
   [-2 + 2*I],
   [       1]])]),
 (2*I,
  1,
  [Matrix([
   [-2 - 2*I],
   [       1]])])]

sistema = [
    sp.Eq(y1(x).diff(x), 2*y1(x) + 8*y2(x)),
    sp.Eq(y2(x).diff(x),  -y1(x) - 2*y2(x))
]
sp.dsolve(sistema)

[Eq(y1(x), -(2*C1 - 2*C2)*cos(2*x) + (2*C1 + 2*C2)*sin(2*x)),
 Eq(y2(x), C1*cos(2*x) - C2*sin(2*x))]

Cálculo de soluciones particulares de sistemas completos#

Al igual que ocurría en el caso de las ecuaciones lineales de coeficientes constantes, a la hora de calcular soluciones particulares de sistemas no homogéneos existen diferentes alternativas. El método de los coeficientes indeterminados también puede ser aplicado, y probar soluciones particulares con una estructura similar al tipo de funciones que intervienen en los términos que forman \(G(x)\).

Ejemplo:

Dado el sistema no homogéneo

\[\begin{split}\begin{array}{l} \frac{dy_1}{dx} = 6y_1+y_2 +6x\\ \frac{dy_2}{dx} = 4y_1+3y_2-10x+4 \end{array}\end{split}\]

en primer lugar debe encontrarse la solución general del sistema homogéneo, para lo que se empieza por calcular los autovalores de la matriz de coeficientes.

\[\begin{split}\left| \begin{array}{cc} 6-\lambda & 1 \\ 4 & 3-\lambda \\ \end{array} \right|=\lambda^2-9\lambda+14=0 \Rightarrow \lambda_1=2,\;\;\lambda_2=7\end{split}\]

Para calcular un autovector asociado a \(\lambda_1=2\) se debe resolver el sistema

\[\begin{split}\left( \begin{array}{cc} 4 & 1 \\ 4 & 1 \\ \end{array} \right) \left(\begin{array}{c}k_1 \\ k_2 \\\end{array}\right)= \left(\begin{array}{c}0 \\ 0 \\\end{array}\right)\end{split}\]

de donde se saca la relación \(k_2=-k_1\), por lo que un autovector sería:

\[\begin{split}\vec{v}_1=\left(\begin{array}{c}1 \\ -4\\\end{array}\right)\end{split}\]

El proceso se repite para el segundo autovalor \(\lambda_2=7\), obteniéndose

\[\begin{split}\left( \begin{array}{cc} -1 & 1 \\ 4 & -4 \\ \end{array} \right) \left(\begin{array}{c}k_1 \\ k_2 \\\end{array}\right)= \left(\begin{array}{c}0 \\ 0 \\\end{array}\right)\end{split}\]

y por tanto son autovectores todos los de la forma \((k,k)\), en particular se toma

\[\begin{split}\vec{v}_2=\left(\begin{array}{c}1 \\ 1\\\end{array}\right)\end{split}\]

De esta forma, la solución general del sistema homogéneo es

\[\begin{split}Y_h=c_1\left(\begin{array}{c}1 \\ -4\\\end{array}\right)e^{2x} + c_2\left(\begin{array}{c}1 \\ 1\\\end{array}\right)e^{7x}\end{split}\]

Ahora es necesario encontrar una solución particular del sistema completo. Como \(G(x)\) está definido por funciones polinómicas de grado 1, se tratará de buscar como solución particular una que esté formada también por polinomios de grado 1, es decir:

\[\begin{split}Y_p=\left(\begin{array}{c}a_0+a_1x \\ b_0+b_1x\\\end{array}\right)\end{split}\]

Para que \(Y_p\) sea realmente una solución particular debería cumplir el sistema, y por tanto se tendría que verificar

\[\begin{split}\begin{array}{l} a_1 = 6(a_0+a_1x)+(b_0+b_1x)+6x \\ b_1 = 4(a_0+a_1x)+3(b_0+b_1x)-10x+4 \end{array}\end{split}\]

Igualando los coeficientes en las expresiones anteriores se obtiene un sistema de 4 ecuaciones que permite encontrar los valores de los parámetros:

\[\begin{split} \left\{ \begin{array}{l} 6a_1+b_1+6=0 \\ 6a_0+b_0=a_1 \\ 4a_1+3b_1-10=0 \\ 4a_0+3b_0+4=b_1 \end{array} \right. \end{split}\]

La solución de este sistema es \(a_0=-4/7\), \(a_1=-2\), \(b_0=10/7\) y \(b_1=6\), por tanto la solución general del sistema inicial es

\[\begin{split} Y=c_1\left(\begin{array}{c}1 \\ -4\\\end{array}\right)e^{2x} + c_2\left(\begin{array}{c}1 \\ 1\\\end{array}\right)e^{7x} + \left(\begin{array}{c}-\frac{4}{7}-2x \\ \frac{10}{7}+6x \\\end{array}\right) \end{split}\]

o equivalentemente

\[\begin{split}\begin{array}{l} y_1 = c_1e^{2x}+c_2e^{7x}-\frac{4}{7}-2x \\ y_2 = -4c_1e^{2x}+c_2e^{7x}+\frac{10}{7}+6x \end{array}\end{split}\]

siendo \(c_1\) y \(c_2\) dos constantes arbitrarias.

La comprobación en Python es la siguiente:

sistema = [
    sp.Eq(y1(x).diff(x), 6*y1(x) +   y2(x) + 6*x),
    sp.Eq(y2(x).diff(x), 4*y1(x) + 3*y2(x) - 10*x + 4)
]
sp.dsolve(sistema)

[Eq(y1(x), -C1*exp(2*x)/4 + C2*exp(7*x) - 2*x - 4/7),
 Eq(y2(x), C1*exp(2*x) + C2*exp(7*x) + 6*x + 10/7)]

Al igual que ocurre con las ecuaciones diferenciales, la determinación de los valores de las constantes arbitrarias requiere exigir el cumplimiento de condiciones sobre las soluciones. Por ejemplo, si en este sistema se exige que se cumpla

\[y_1(0)=2,\;\;y_2(0)=5\]

la solución del sistema sería:

sistema = [
    sp.Eq(y1(x).diff(x), 6*y1(x) +   y2(x) + 6*x),
    sp.Eq(y2(x).diff(x), 4*y1(x) + 3*y2(x) - 10*x + 4)
]
condiciones = {y1(0):2, y2(0):5}
sp.dsolve(sistema, ics=condiciones)

[Eq(y1(x), -2*x + 97*exp(7*x)/35 - exp(2*x)/5 - 4/7),
 Eq(y2(x), 6*x + 97*exp(7*x)/35 + 4*exp(2*x)/5 + 10/7)]

Resolución numérica de sistemas de ecuaciones diferenciales#

En muchos sistemas de ecuaciones diferenciales no queda más remedio que recurrir a métodos numéricos de aproximación de las soluciones. La función solve_ivp() del paquete SciPy puede ser usada para ello. A continuación se muestra un ejemplo.

Ejemplo:

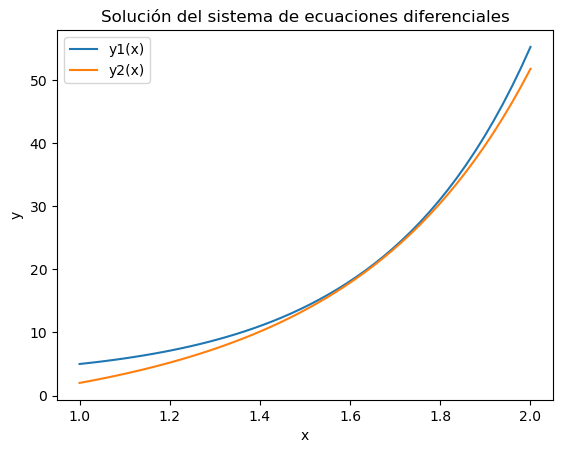
Dado el siguiente sistema con las condiciones iniciales para las funciones

\[\begin{split}\left\{ \begin{array}{l} y_1'= x y_1+y_2+\frac{1}{x+1}\\ y_2'= 2 y_1+\frac{1}{x}y_2 +\sqrt{x}\\ y_1(1)=5,\;\;y_2(1)=2 \end{array} \right.\end{split}\]

Se puede comprobar que la resolución simbólica con las opciones de SymPy es imposible. A continuación se muestra el proceso de resolución numérica.

import numpy as np
from scipy.integrate import solve_ivp

def Fproblema(x, Y):
    y1, y2 = Y
    dy1 = x*y1 + y2 + 1/(x+1)
    dy2 = 2*y1 + (1/x)*y2 + np.sqrt(x)
    return [dy1, dy2]

intervalo = [1, 2]
valoresIniciales = [5, 2]

xs = np.linspace(1, 2)
solucion = solve_ivp(Fproblema, intervalo, valoresIniciales, t_eval=xs)
print(solucion)

  message: 'The solver successfully reached the end of the integration interval.'
     nfev: 26
     njev: 0
      nlu: 0
      sol: None
   status: 0
  success: True
        t: array([1.        , 1.02040816, 1.04081633, 1.06122449, 1.08163265,
       1.10204082, 1.12244898, 1.14285714, 1.16326531, 1.18367347,
       1.20408163, 1.2244898 , 1.24489796, 1.26530612, 1.28571429,
       1.30612245, 1.32653061, 1.34693878, 1.36734694, 1.3877551 ,
       1.40816327, 1.42857143, 1.44897959, 1.46938776, 1.48979592,
       1.51020408, 1.53061224, 1.55102041, 1.57142857, 1.59183673,
       1.6122449 , 1.63265306, 1.65306122, 1.67346939, 1.69387755,
       1.71428571, 1.73469388, 1.75510204, 1.7755102 , 1.79591837,
       1.81632653, 1.83673469, 1.85714286, 1.87755102, 1.89795918,
       1.91836735, 1.93877551, 1.95918367, 1.97959184, 2.        ])
 t_events: None
        y: array([[ 5.        ,  5.15841592,  5.32793812,  5.50919058,  5.70291138,
         5.90984023,  6.13063317,  6.36602288,  6.61681959,  6.88391108,
         7.1682627 ,  7.47091734,  7.79299547,  8.13569509,  8.50029177,
         8.88813864,  9.30066638,  9.73938324, 10.20587501, 10.70180504,
        11.22891424, 11.78914403, 12.38573595, 13.02059754, 13.69543016,
        14.41225886, 15.17343244, 15.98162339, 16.83982792, 17.75136596,
        18.71988114, 19.74934082, 20.84403605, 22.00858162, 23.24791601,
        24.56730143, 25.9723238 , 27.46889274, 29.06324159, 30.76192742,
        32.57183099, 34.50015679, 36.55443301, 38.74251155, 41.0725971 ,
        43.55546677, 46.20273462, 49.02591032, 52.03740229, 55.25051774],
       [ 2.        ,  2.27090358,  2.55332761,  2.84778518,  3.15485555,
         3.47512852,  3.80917462,  4.1576213 ,  4.52115337,  4.90051299,
         5.29649967,  5.70997026,  6.14183899,  6.59307741,  7.06471444,
         7.55783635,  8.07358674,  8.6131666 ,  9.17783424,  9.76890532,
        10.38775288, 11.03586945, 11.71543003, 12.42798058, 13.17500995,
        13.95821716, 14.77951139, 15.64101204, 16.54504863, 17.4941609 ,
        18.49109875, 19.53882225, 20.64050164, 21.79951737, 23.01946001,
        24.30413037, 25.65753937, 27.08390816, 28.58766804, 30.17346048,
        31.84613714, 33.61075985, 35.47260062, 37.43714162, 39.51009645,
        41.69901366, 44.01194481, 46.45676718, 49.04192381, 51.77642347]])
 y_events: None

for i in range(len(solucion.t)):
    print(f"y1({solucion.t[i]}) = {solucion.y[0][i]};\t y2({solucion.t[i]}) = {solucion.y[1][i]}")

y1(1.0) = 5.0;	 y2(1.0) = 2.0
y1(1.0204081632653061) = 5.158415922593964;	 y2(1.0204081632653061) = 2.2709035826296904
y1(1.0408163265306123) = 5.327938116124668;	 y2(1.0408163265306123) = 2.553327607251078
y1(1.0612244897959184) = 5.509190580121647;	 y2(1.0612244897959184) = 2.847785180763836
y1(1.0816326530612246) = 5.702911380918667;	 y2(1.0816326530612246) = 3.1548555547403034
y1(1.1020408163265305) = 5.909840227366631;	 y2(1.1020408163265305) = 3.475128523990359
y1(1.1224489795918366) = 6.130633170216386;	 y2(1.1224489795918366) = 3.8091746206042827
y1(1.1428571428571428) = 6.366022881639541;	 y2(1.1428571428571428) = 4.157621300428155
y1(1.163265306122449) = 6.616819590583012;	 y2(1.163265306122449) = 4.52115337055039
y1(1.183673469387755) = 6.88391108276902;	 y2(1.183673469387755) = 4.900512989301729
y1(1.2040816326530612) = 7.168262700695092;	 y2(1.2040816326530612) = 5.296499666255241
y1(1.2244897959183674) = 7.470917343634055;	 y2(1.2244897959183674) = 5.709970262226324
y1(1.2448979591836735) = 7.792995467634043;	 y2(1.2448979591836735) = 6.141838989272703
y1(1.2653061224489797) = 8.135695085518497;	 y2(1.2653061224489797) = 6.593077410694431
y1(1.2857142857142856) = 8.500291766886154;	 y2(1.2857142857142856) = 7.064714441033887
y1(1.3061224489795917) = 8.888138638111068;	 y2(1.3061224489795917) = 7.557836346075792
y1(1.3265306122448979) = 9.30066638234259;	 y2(1.3265306122448979) = 8.073586742847175
y1(1.346938775510204) = 9.739383239505372;	 y2(1.346938775510204) = 8.613166599617406
y1(1.3673469387755102) = 10.205875006299378;	 y2(1.3673469387755102) = 9.17783423589818
y1(1.3877551020408163) = 10.701805036199872;	 y2(1.3877551020408163) = 9.768905322443517
y1(1.4081632653061225) = 11.228914239457419;	 y2(1.4081632653061225) = 10.38775288124977
y1(1.4285714285714286) = 11.789144026275315;	 y2(1.4285714285714286) = 11.035869453487546
y1(1.4489795918367347) = 12.385735954061118;	 y2(1.4489795918367347) = 11.715430033899382
y1(1.4693877551020407) = 13.020597544816367;	 y2(1.4693877551020407) = 12.427980584841462
y1(1.489795918367347) = 13.695430156017629;	 y2(1.489795918367347) = 13.175009951698545
y1(1.510204081632653) = 14.412258858395923;	 y2(1.510204081632653) = 13.958217155428343
y1(1.530612244897959) = 15.173432435936805;	 y2(1.530612244897959) = 14.779511392561638
y1(1.5510204081632653) = 15.981623385880308;	 y2(1.5510204081632653) = 15.641012035202188
y1(1.5714285714285714) = 16.83982791872096;	 y2(1.5714285714285714) = 16.545048631026773
y1(1.5918367346938775) = 17.751365958207792;	 y2(1.5918367346938775) = 17.494160903285177
y1(1.6122448979591835) = 18.719881141344317;	 y2(1.6122448979591835) = 18.491098750800194
y1(1.6326530612244898) = 19.749340818388585;	 y2(1.6326530612244898) = 19.538822247967666
y1(1.6530612244897958) = 20.844036052853063;	 y2(1.6530612244897958) = 20.640501644756355
y1(1.6734693877551021) = 22.00858162150482;	 y2(1.6734693877551021) = 21.799517366708162
y1(1.693877551020408) = 23.247916014365302;	 y2(1.693877551020408) = 23.019460014937863
y1(1.7142857142857142) = 24.567301434710554;	 y2(1.7142857142857142) = 24.30413036613335
y1(1.7346938775510203) = 25.972323799071063;	 y2(1.7346938775510203) = 25.65753937255548
y1(1.7551020408163265) = 27.46889273723183;	 y2(1.7551020408163265) = 27.083908162038128
y1(1.7755102040816326) = 29.063241592232334;	 y2(1.7755102040816326) = 28.587668037988166
y1(1.7959183673469385) = 30.761927420366547;	 y2(1.7959183673469385) = 30.173460479385483
y1(1.816326530612245) = 32.571830991183006;	 y2(1.816326530612245) = 31.846137140783036
y1(1.8367346938775508) = 34.50015678748463;	 y2(1.8367346938775508) = 33.610759852306664
y1(1.8571428571428572) = 36.554433005328946;	 y2(1.8571428571428572) = 35.472600619655374
y1(1.8775510204081631) = 38.74251155402784;	 y2(1.8775510204081631) = 37.43714162410103
y1(1.8979591836734693) = 41.072597102821625;	 y2(1.8979591836734693) = 39.51009645236327
y1(1.9183673469387754) = 43.55546677345115;	 y2(1.9183673469387754) = 41.69901365898605
y1(1.9387755102040816) = 46.20273462250072;	 y2(1.9387755102040816) = 44.01194480729432
y1(1.9591836734693877) = 49.02591031922097;	 y2(1.9591836734693877) = 46.45676718302671
y1(1.9795918367346939) = 52.03740229361062;	 y2(1.9795918367346939) = 49.041923813753186
y1(2.0) = 55.25051773641643;	 y2(2.0) = 51.77642346887501

import matplotlib.pyplot as plt
plt.plot(xs, solucion.y[0], label='y1(x)')
plt.plot(xs, solucion.y[1], label='y2(x)')
plt.xlabel('x'); plt.ylabel('y')
plt.title('Solución del sistema de ecuaciones diferenciales')
plt.legend()
plt.show()
_images/2d1e73e4923d7c37d124902ad959329a07a2db2e3b10a48e47091f5c5d355cf4.png

Ejemplo:

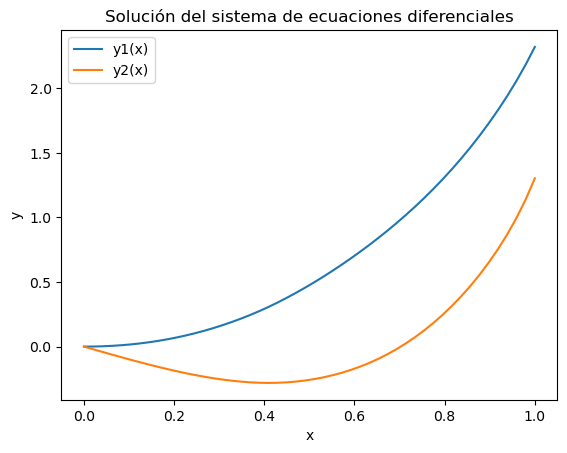
El siguiente sistema tampoco es resoluble simbólicamente. En este caso se trata de un sistema no lineal.

\[\begin{split}\left\{\begin{array}{l} y_1' = y_1 + y_2^2 + 3t \\ y_2' = 3y_1 + y_2^3 - cos(t) \end{array}\right.\end{split}\]

Si se consideran las condiciones iniciales \(y_1(0)=y_2(0)=0\), la solución numérica sería:

def Fproblema(t, Y):
    y1, y2 = Y
    dy1 = y1 + y2**2 + 3*t
    dy2 = 3*y1 + y2**3 - np.cos(t)
    return [dy1, dy2]

intervalo = [0, 1]
valoresIniciales = [0, 0]

xs = np.linspace(0, 1)
solucion = solve_ivp(Fproblema, intervalo, valoresIniciales, t_eval=xs)
print(solucion)

  message: 'The solver successfully reached the end of the integration interval.'
     nfev: 44
     njev: 0
      nlu: 0
      sol: None
   status: 0
  success: True
        t: array([0.        , 0.02040816, 0.04081633, 0.06122449, 0.08163265,
       0.10204082, 0.12244898, 0.14285714, 0.16326531, 0.18367347,
       0.20408163, 0.2244898 , 0.24489796, 0.26530612, 0.28571429,
       0.30612245, 0.32653061, 0.34693878, 0.36734694, 0.3877551 ,
       0.40816327, 0.42857143, 0.44897959, 0.46938776, 0.48979592,
       0.51020408, 0.53061224, 0.55102041, 0.57142857, 0.59183673,
       0.6122449 , 0.63265306, 0.65306122, 0.67346939, 0.69387755,
       0.71428571, 0.73469388, 0.75510204, 0.7755102 , 0.79591837,
       0.81632653, 0.83673469, 0.85714286, 0.87755102, 0.89795918,
       0.91836735, 0.93877551, 0.95918367, 0.97959184, 1.        ])
 t_events: None
        y: array([[ 0.00000000e+00,  6.31832199e-04,  2.55603672e-03,
         5.81622315e-03,  1.04560810e-02,  1.65193072e-02,
         2.40494509e-02,  3.30894113e-02,  4.36816540e-02,
         5.58669400e-02,  6.96842016e-02,  8.51705427e-02,
         1.02361238e-01,  1.21289736e-01,  1.41987653e-01,
         1.64484780e-01,  1.88809078e-01,  2.14986679e-01,
         2.43041889e-01,  2.73048773e-01,  3.05306927e-01,
         3.39736640e-01,  3.76208493e-01,  4.14616471e-01,
         4.54877956e-01,  4.96933729e-01,  5.40747971e-01,
         5.86308262e-01,  6.33625581e-01,  6.82734306e-01,
         7.33692216e-01,  7.86580488e-01,  8.41503697e-01,
         8.98589820e-01,  9.57990230e-01,  1.01987970e+00,
         1.08445641e+00,  1.15194193e+00,  1.22258122e+00,
         1.29664267e+00,  1.37441804e+00,  1.45622250e+00,
         1.54239603e+00,  1.63336716e+00,  1.72953577e+00,
         1.83149416e+00,  1.94013056e+00,  2.05662915e+00,
         2.18247005e+00,  2.31942932e+00],
       [ 0.00000000e+00, -2.03939259e-02, -4.07019286e-02,
        -6.08366201e-02, -8.07088098e-02, -1.00227485e-01,
        -1.19299782e-01, -1.37830776e-01, -1.55723113e-01,
        -1.72876588e-01, -1.89188129e-01, -2.04551785e-01,
        -2.18858737e-01, -2.31997288e-01, -2.43852871e-01,
        -2.54308045e-01, -2.63242496e-01, -2.70533035e-01,
        -2.76053603e-01, -2.79641161e-01, -2.80976183e-01,
        -2.79983460e-01, -2.76622101e-01, -2.70837776e-01,
        -2.62562716e-01, -2.51715715e-01, -2.38202125e-01,
        -2.21913863e-01, -2.02729405e-01, -1.80513788e-01,
        -1.55118612e-01, -1.26382038e-01, -9.41287859e-02,
        -5.81701399e-02, -1.83039441e-02,  2.56853962e-02,
         7.40269140e-02,  1.26963081e-01,  1.84749809e-01,
         2.47656446e-01,  3.15965780e-01,  3.89974038e-01,
         4.70002026e-01,  5.57066273e-01,  6.51818643e-01,
         7.55147450e-01,  8.68813760e-01,  9.95451395e-01,
         1.13856693e+00,  1.30253968e+00]])
 y_events: None

for i in range(len(solucion.t)):
    print(f"y1({solucion.t[i]}) = {solucion.y[0][i]};\t y2({solucion.t[i]}) = {solucion.y[1][i]}")

y1(0.0) = 0.0;	 y2(0.0) = 0.0
y1(0.02040816326530612) = 0.0006318321991198569;	 y2(0.02040816326530612) = -0.020393925858306225
y1(0.04081632653061224) = 0.002556036719002805;	 y2(0.04081632653061224) = -0.04070192863406483
y1(0.061224489795918366) = 0.005816223153269381;	 y2(0.061224489795918366) = -0.06083662011673597
y1(0.08163265306122448) = 0.010456081029983532;	 y2(0.08163265306122448) = -0.08070880975129804
y1(0.1020408163265306) = 0.01651930718639061;	 y2(0.1020408163265306) = -0.10022748529304112
y1(0.12244897959183673) = 0.024049450932334605;	 y2(0.12244897959183673) = -0.11929978206807763
y1(0.14285714285714285) = 0.033089411272003474;	 y2(0.14285714285714285) = -0.137830776438679
y1(0.16326530612244897) = 0.04368165401997527;	 y2(0.16326530612244897) = -0.15572311251840001
y1(0.18367346938775508) = 0.05586694002964605;	 y2(0.18367346938775508) = -0.17287658834737105
y1(0.2040816326530612) = 0.06968420164307196;	 y2(0.2040816326530612) = -0.18918812876667065
y1(0.22448979591836732) = 0.08517054269096916;	 y2(0.22448979591836732) = -0.20455178541832553
y1(0.24489795918367346) = 0.10236123849271393;	 y2(0.24489795918367346) = -0.21885873674531045
y1(0.26530612244897955) = 0.12128973585634249;	 y2(0.26530612244897955) = -0.2319972879915484
y1(0.2857142857142857) = 0.14198765307855127;	 y2(0.2857142857142857) = -0.24385287120191046
y1(0.3061224489795918) = 0.1644847799446966;	 y2(0.3061224489795918) = -0.25430804522221584
y1(0.32653061224489793) = 0.1888090777287951;	 y2(0.32653061224489793) = -0.26324249569923197
y1(0.3469387755102041) = 0.21498667919352318;	 y2(0.3469387755102041) = -0.2705330350806744
y1(0.36734693877551017) = 0.24304188859021741;	 y2(0.36734693877551017) = -0.2760536026152067
y1(0.3877551020408163) = 0.273048772609798;	 y2(0.3877551020408163) = -0.2796411612320948
y1(0.4081632653061224) = 0.30530692721221075;	 y2(0.4081632653061224) = -0.2809761831721182
y1(0.42857142857142855) = 0.3397366395061373;	 y2(0.42857142857142855) = -0.27998346017152215
y1(0.44897959183673464) = 0.37620849322465333;	 y2(0.44897959183673464) = -0.27662210106416224
y1(0.4693877551020408) = 0.41461647135540664;	 y2(0.4693877551020408) = -0.27083777596820646
y1(0.4897959183673469) = 0.4548779561406158;	 y2(0.4897959183673469) = -0.26256271628613564
y1(0.5102040816326531) = 0.49693372907707134;	 y2(0.5102040816326531) = -0.2517157147047431
y1(0.5306122448979591) = 0.5407479709161346;	 y2(0.5306122448979591) = -0.23820212519513492
y1(0.5510204081632653) = 0.5863082616637393;	 y2(0.5510204081632653) = -0.22191386301272964
y1(0.5714285714285714) = 0.6336255805803899;	 y2(0.5714285714285714) = -0.20272940469725856
y1(0.5918367346938775) = 0.6827343061811625;	 y2(0.5918367346938775) = -0.18051378807276558
y1(0.6122448979591836) = 0.7336922162357042;	 y2(0.6122448979591836) = -0.1551186122476074
y1(0.6326530612244897) = 0.7865804877682352;	 y2(0.6326530612244897) = -0.1263820376144528
y1(0.6530612244897959) = 0.8415036970575447;	 y2(0.6530612244897959) = -0.09412878585028392
y1(0.673469387755102) = 0.8985898196369952;	 y2(0.673469387755102) = -0.05817013991639505
y1(0.6938775510204082) = 0.9579902302945205;	 y2(0.6938775510204082) = -0.018303944058393307
y1(0.7142857142857142) = 1.0198797030726239;	 y2(0.7142857142857142) = 0.025685396193801446
y1(0.7346938775510203) = 1.0844564112683832;	 y2(0.7346938775510203) = 0.07402691402595724
y1(0.7551020408163265) = 1.1519419274334455;	 y2(0.7551020408163265) = 0.12696308133952894
y1(0.7755102040816326) = 1.22258122337403;	 y2(0.7755102040816326) = 0.18474980875165908
y1(0.7959183673469387) = 1.2966426701509268;	 y2(0.7959183673469387) = 0.24765644559517686
y1(0.8163265306122448) = 1.3744180380794986;	 y2(0.8163265306122448) = 0.3159657799186003
y1(0.836734693877551) = 1.4562224967296789;	 y2(0.836734693877551) = 0.3899740384861331
y1(0.8571428571428571) = 1.5423960251807625;	 y2(0.8571428571428571) = 0.4700020261847724
y1(0.8775510204081632) = 1.6333671563557888;	 y2(0.8775510204081632) = 0.5570662733091746
y1(0.8979591836734693) = 1.729535772287725;	 y2(0.8979591836734693) = 0.6518186429876454
y1(0.9183673469387754) = 1.8314941634206912;	 y2(0.9183673469387754) = 0.7551474496524015
y1(0.9387755102040816) = 1.9401305640140574;	 y2(0.9387755102040816) = 0.8688137604193148
y1(0.9591836734693877) = 2.0566291521424462;	 y2(0.9591836734693877) = 0.9954513950879135
y1(0.9795918367346939) = 2.182470049695732;	 y2(0.9795918367346939) = 1.1385669261413822
y1(1.0) = 2.3194293223790408;	 y2(1.0) = 1.3025396787465624

plt.plot(xs, solucion.y[0], label='y1(x)')
plt.plot(xs, solucion.y[1], label='y2(x)')
plt.xlabel('x'); plt.ylabel('y')
plt.title('Solución del sistema de ecuaciones diferenciales')
plt.legend()
plt.show()
_images/b8eab5d046ea01c789fa4d9d1dfc553e8bcbf09bc976bba008ae959eceab3a22.png

Ejercicios propuestos#

  • Resolver las siguientes sistemas homogéneos de ecuaciones diferenciales:

\[\begin{split}\left\{ \begin{array}{l} y_1'=2y_1+y_2\\ y_2'=3y_1+4y_2 \end{array} \right.\end{split}\]
\[\begin{split}\left\{ \begin{array}{l} y_1'=4y_1-y_2\\ y_2'=-4y_1+4y_2 \end{array} \right.\end{split}\]
\[\begin{split}\left\{ \begin{array}{l} y_1'=-y_1+y_2\\ y_2'=-6y_1+4y_2 \end{array} \right.\end{split}\]

  • Resolver las siguientes sistemas homogéneos de ecuaciones diferenciales:

\[\begin{split}\left\{ \begin{array}{l} y_1'=y_3 \\ y_2'=y_1-3y_3 \\ y_3'=y_2+3y_3 \end{array} \right.\end{split}\]
\[\begin{split}\left\{ \begin{array}{l} y_1'=y_1-y_3 \\ y_2'=13y_2 \\ y_3'=y_1+y_3 \end{array} \right.\end{split}\]
\[\begin{split}\left\{ \begin{array}{l} y_1'=3y_1+2y_2+4y_3 \\ y_2'=2y_1+2y_3 \\ y_3'=4y_1+2y_2+3y_3 \end{array} \right.\end{split}\]

  • Encontrar la solución del siguiente sistema cumpliendo las condiciones iniciales \(y_1(0)=0\), \(y_2(0)=1\)

\[\begin{split}\left\{ \begin{array}{l} y_1'=y_1+12y_2\\ y_2'=3y_1+y_2 \end{array} \right.\end{split}\]

  • Resolver los siguientes sistemas no homogéneos

\[\begin{split}\left\{ \begin{array}{l} y_1'=-y_1+4y_2+e^x\\ y_2'=y_1-y_2+1 \end{array} \right.\end{split}\]
\[\begin{split}\left\{ \begin{array}{l} y_1'=y_1+12y_2+2x\\ y_2'=3y_1+y_2+x \end{array} \right.\end{split}\]
\[\begin{split}\left\{ \begin{array}{l} y_1'=y_2-5\cos x\\ y_2'=2y_1+y_2 \end{array} \right.\end{split}\]

  • Resolver el siguiente sistema no homogéneo:

\[\begin{split} \left\{ \begin{array}{l} y_1'=-y_1+y_2+y_3+e^x\\ y_2'=y_1-y_2+y^3+e^{3x}\\ y_3'=y_1+y_2+y_3+4 \end{array} \right. \end{split}\]