Cambios de variable en integrales dobles

En ocasiones la resolución de una integral doble puede facilitarse enormemente mediante la realización de un cambio en las variables de integración. Como caso particular, en esta sección se muestra la resolución de integrales dobles en coordenadas polares; para posteriormente presentar el método general de cambio de variables.

Integración en coordenadas polares

Un punto \((x,y)\in R^2\) puede ser también expresado en coordenadas polares \((r,\theta)\), donde \(r\) representa la distancia del punto al origen y \(\theta\) el ángulo que forma la unión del punto con el origen con respecto al eje \(OX\). La equivalencia entre ambos tipos de representación de puntos del plano viene dada por las expresiones:

\[x = r\cos(\theta)\]

\[y = r\sin(\theta)\]

A la hora de subdividir la región de integración en subdominios mediante la consideración de pequeños incrementos en las coordenadas de los puntos de subdivisión, en el caso de coordenadas cartesianas se forman rectángulos cuyas áreas vienen dadas por \(\Delta A=\Delta x\,\Delta y\). Sin embargo, en el caso de coordenadas polares se formarían pequeños rectángulos con lados curvos, tal como puede verse en la figura

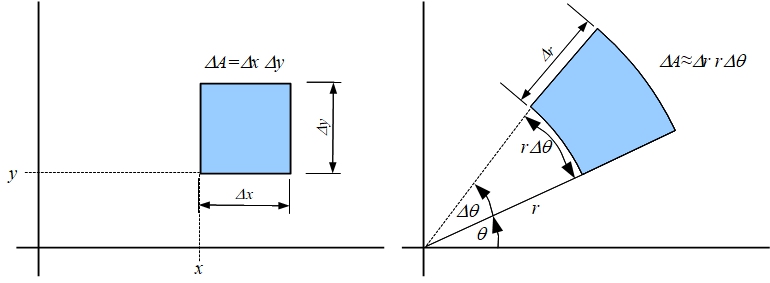
En este caso las áreas de esos rectángulos pueden ser aproximadas de la siguiente manera:

\[\Delta A\approx r\,\Delta \theta\,\Delta r\]

Al considerar áreas infinitesimales, haciendo tender a cero los incrementos sobre las respectivas coordenadas, se obtendría la equivalencia para los elementos diferenciales de áreas \(dA\) cuando se trabaja en coordenadas cartesianas y polares:

\[dA = dx\,dy = r\,d\theta\,dr\]

Por tanto, a la hora de calcular una integral doble en coordenadas polares debería realizarse el cambio en las variables de la función \(f(x,y)\) utilizando las equivalencias anteriores, pero también en el elemento \(dA\) utilizando \(dA = r\,d\theta\,dr\).

Entre las posibilidades del paquete Matplotlib de Python está la de realizar representaciones gráficas en el espacio de coordenadas polares, en lugar de coordenadas cartesianas

import matplotlib.pyplot as plt
ax = plt.subplot(projection='polar');

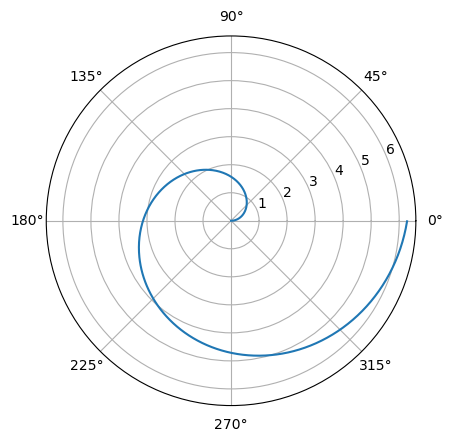
y realizar representaciones de curvas en coordenadas polares sobre ese plano, tal como se muestra en este ejemplo:

import numpy as np
r = np.arange(0, 2*np.pi, 0.01)
theta = r
plt.polar(r, theta);

Volviendo al cálculo de integrales dobles, a continuación se muestra un ejemplo de integral doble que puede ser resuelto con facilidad haciendo uso de las coordenadas polares.

---

Ejemplo:

Considérese la integral doble

\[I=\iint\limits_R \sqrt{x^2+y^2}dA\]

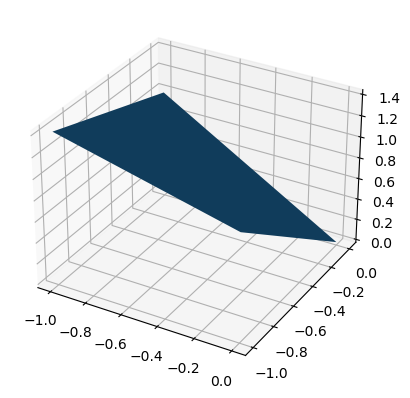
donde \(R\) es el recinto delimitado por las condiciones \(x^2+y^2\leq 1\) y \(x\geq 0\). Con las correspondientes opciones de Matplotlib pueden obtenerse representaciones gráficas de la función y de la región de integración. En este caso la región de integración es el semicírculo de radio \(1\) y centro \((0,0)\) correspondiente a la parte positiva del eje \(OX\).

X, Y = np.meshgrid(np.arange(-1,1), np.arange(-1,1))
Z = np.sqrt(X**2 + Y**2)
ax = plt.subplot(projection='3d');
ax.plot_surface(X, Y, Z)
plt.show()

El paquete SymPy dispone de funciones para realizar representaciones gráficas de funciones simbólicas o de ecuaciones implícitas (https://docs.sympy.org/latest/modules/plotting.html). Con dichas funciones puede obtenerse una representación del dominio de integración.

La representación gráfica de ecuaciones puede realizarse con la función plot_implicit(), que admite incluso la posibilidad de representar no solo igualdades, sino también algunas desigualdades sencillas.

import sympy as sp
x,y = sp.symbols('x,y')
sp.plot_implicit(sp.And(x**2+y**2<=1, x>=0), (x, 0, 2), (y, -1, 1));

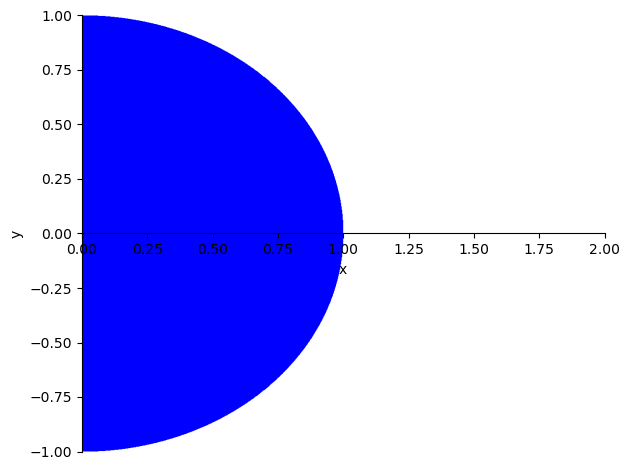
Tanto la función a integrar como el recinto de integración de este ejemplo resultan muy adecuadas para el cambio a coordenadas polares. En lo que se refiere al recinto, se observa cómo fijado un ángulo \(\theta\in[-\pi/2,\pi/2]\) la distancia al origen \(r\) varía entre los valores \(r_{min}=0\) y \(r_{max}=1\)

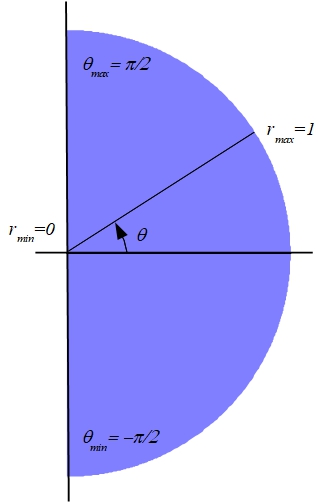
Haciendo el cambio a coordenadas polares mediante las expresiones que definen el cambio, teniendo en cuenta además que \(\cos^2\theta+\sin^2\theta=1\), la integral doble puede calcularse en la siguiente forma:

\[\iint\limits_R \sqrt{x^2+y^2}\,\,dA= \iint\limits_R \sqrt{r^2\cos^2\theta+r^2\sin^2\theta}\,\,r\,d\theta dr= \int_{0}^{1}\left(\int_{-\pi/2}^{\pi/2}r^2\,d\theta\right)dr\]

Se procede en primer lugar a calcular la integral interior:

\[\int_{-\pi/2}^{\pi/2}r^2\,d\theta = \left.r^2\theta\right|_{\theta=-\pi/2}^{\theta=\pi/2}=\pi r^2\]

y posteriormente la integral exterior

\[I=\int_{0}^{1}\pi r^2\,dr = \left. \pi\frac{r^3}{3}\right|_{r=0}^{r=1}=\frac{\pi}{3}\]

Se comprueba en Python como se podría calcular la integral en coordenadas polares. Es importante señalar que la definición de las variables \(x,y\) en coordenadas polares debe realizarse antes de definir la función.

import sympy as sp
x,y,r,t = sp.symbols('x,y,r,t')
x = r*sp.cos(t)
y = r*sp.sin(t)
F = sp.sqrt(x**2 + y**2)
sp.integrate(F*r, (t, -sp.pi/2, sp.pi/2), (r, 0, 1))

\[\displaystyle \frac{\pi}{3}\]

---

Algunas integrales dobles resultan más sencillas de plantear y resolver si se realiza un paso a coordenadas polares. Obviamente en Python también es posible resolver dichas integrales aunque, como se ha visto en el ejemplo anterior, la instrucción de integración no realiza directamente el cambio. En el siguiente ejemplo puede verse otro ejemplo de cambio de variable a coordenadas polares.

---

Ejemplo:

Se desea calcular el valor de la integral

\[\iint_D\frac{1}{\sqrt{x^2+y^2}}dA\]

siendo \(D\) el recinto delimitado por \(2\leq x^2+y^2\leq4\), \(x\leq y\).

Usando las funciones de representación gráfica del paquete SymPy se puede obtener una visualización del dominio de integración.

x,y = sp.symbols('x,y')
sp.plot_implicit(sp.And(x**2+y**2>2, x**2+y**2<4, x<y), (x,-3,3), (y,-3,3));

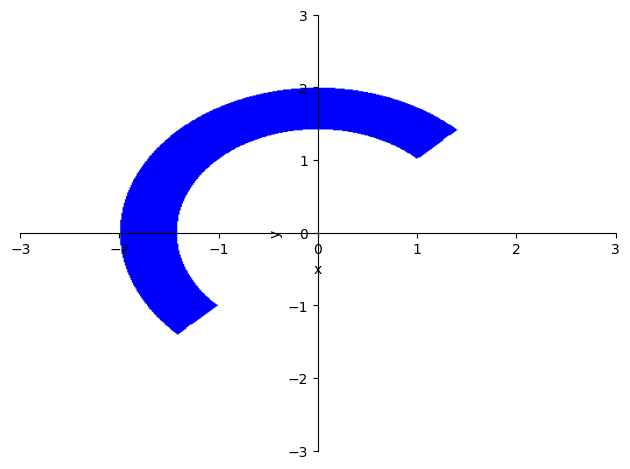
A la vista de las restricciones que delimitan el recinto de integración parece claro que la integral resulta más fácil de plantear en coordenadas polares. Para ello se comienza por definir las dos nuevas coordenadas simbólicas y realizar el cambio sobre la integral.

r,t = sp.symbols('r,t')

x = r*sp.cos(t)
y = r*sp.sin(t)
F = 1/sp.sqrt(x**2+y**2)

En el recinto de integración (\(2\leq x^2+y^2\leq4\), \(x\leq y\)) la variable \(r\) varía entre \(\sqrt{2}\) y \(2\), mientras que \(t\) varía entre \(\frac{\pi}{4}\) y \(\frac{5\pi}{4}\), por lo que la integral final se calcularía de la siguiente manera:

sp.integrate(F * r, (r, sp.sqrt(2), 2), (t, sp.pi/4, 5*sp.pi/4))

\[\displaystyle - \sqrt{2} \pi + 2 \pi\]

Es importante recordar multiplicar por la variable \(r\) a la función antes de proceder a la integración en polares.

---

Ejemplo:

Como ejemplo de aplicación de la integración doble en coordenadas polares se muestra a continuación el cálculo del área de la conocida como lemiscata de Bernouilli.

La lemiscata de Bernouilli es una curva paramétrica cerrada definida por

\[r^2=a^2\cos 2\theta\]

y cuya representación paramétrica en coordenadas cartesianas sería:

\[x=\frac{a\cos t}{\sin^2 t+1};\;\;\;\;\;y=\frac{a\cos t\sin t}{\sin^2 t+1}\]

Por ejemplo, con el siguiente código Python puede obtenerse la representación gráfica para el caso \(a=1\):

t = np.linspace(0, 2*np.pi, num=1000)
x = np.cos(t) / (np.sin(t)**2 + 1)
y = np.cos(t) * np.sin(t) / (np.sin(t)**2 + 1)
plt.axis('equal')
plt.plot(x, y);

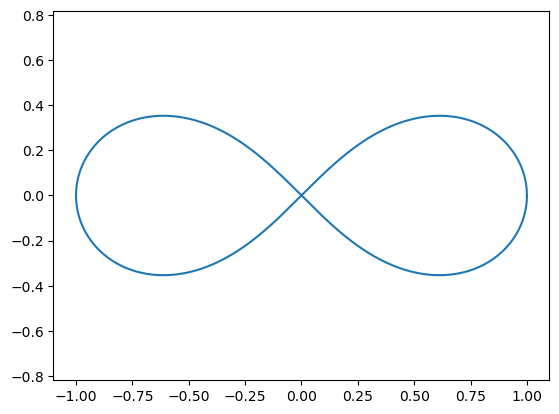
Como puede apreciarse en dicha gráfica, la curva es totalmente simétrica por lo que para calcular el área bastaría calcular el área de la parte \(L_p\) que se encuentra en el semiplano correspondiente a \(x\geq 0\) y posteriormente multiplicarla por dos.

Teniendo en cuenta la ecuación paramétrica que define la curva en polares, los valores admisibles para \(\theta\) en el semiplano \(x\geq 0\) son aquellos que hacen que \(\cos 2\theta\geq 0\), por tanto \(\theta\) variará entre \(-\pi/4\) y \(\pi/4\).

Fijado un ángulo \(\theta\) el radio \(r\) variará entre los valores \(0\) y \(\sqrt{a^2\cos 2\theta}\). En definitiva, se tendría que calcular en primer lugar la integral doble en coordenadas polares:

\[\iint\limits_{L_p} dA= \int_{-\pi/4}^{\pi/4}\left(\int_{0}^{\sqrt{a^2\cos 2\theta}}r\,dr\right)d\theta\]

La integral interna es:

\[\int_{0}^{\sqrt{a^2\cos 2\theta}}r\,dr= \left.\frac{r^2}{2}\right|_{r=0}^{r=\sqrt{a^2\cos 2\theta}}= \frac{a^2\cos 2\theta}{2}\]

Y la integral externa:

\[Area(L_p)= \int_{-\pi/4}^{\pi/4} \frac{a^2\cos 2\theta}{2}\,d\theta = \left.a^2\frac{\sin 2\theta}{4}\right|_{\theta=-\pi/4}^{\theta=\pi/4}= \frac{a^2}{2}\]

Por tanto el área de la lemiscata completa es \(a^2\).

Esa misma integral puede calcularse con ayuda de Python:

r,t,a = sp.symbols('r,t,a')
sp.integrate(r, (r, 0, sp.sqrt(a**2*sp.cos(2*t))), (t, -sp.pi/4, sp.pi/4))

\[\displaystyle \frac{a^{2}}{2}\]

Aplicación de un cambio de variables

La aplicación de un cambio de variables tiene por objeto tratar de simplificar la función a integrar y/o la parametrización de la región de integración. La integración en coordenadas polares no es más que un caso particular de cambio de variable que ha servido para comprobar cómo al aplicar un cambio se ven afectados los tres elementos de la integral: la función, la región de integración y el elemento diferencial de área. Tomando como punto de partida lo visto en la sección anterior, en ésta se trata de presentar un marco general para la aplicación de cualquier cambio de variables sobre una integral doble.

Para comenzar, se analiza un caso particular de aplicación de un cambio de variables de naturaleza lineal, para comprobar cómo se ven afectados por los cambios los elementos diferenciales de área. Por ejemplo, considérese el cambio:

\[ x = \frac{u-v}{2} \]

\[ y = \frac{u+v}{2} \]

o equivalentemente su cambio inverso:

\[u=x+y\]

\[v=-x+y\]

Si se toma como elemento de área el cuadrado unidad \(A=[0,1]\times[0,1]\), el cambio de variables convertiría ese elemento en un paralelogramo \(A'\) tal como se muestra en la figura siguiente:

x = np.array([0, 1, 1, 0])
y = np.array([0, 0, 1, 1])
u = x+y
v = y-x
fig, ax = plt.subplots(1, 2, sharey=True, figsize=(10, 4))
ax[0].axis('equal')
ax[0].fill(x, y, color='blue') 
ax[0].set_title('Dominio inicial')
ax[1].axis('equal')
ax[1].fill(u, v, color='cyan')
ax[1].set_title('Dominio tras el cambio')
plt.show()

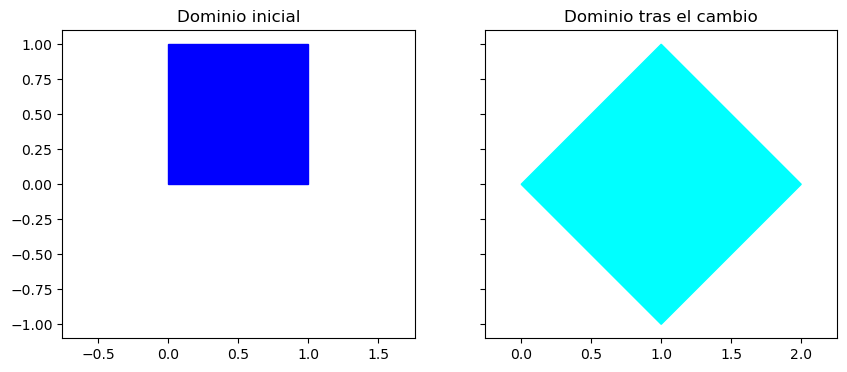
Como puede apreciarse, dicho cambio afecta al área de ese elemento, pasando de un área igual a \(1\) a un área igual a \(2\). Ese factor multiplicativo coincide con el valor del determinante de la matriz que define el cambio \(u=x+y\), \(v=-x+y\):

\[\begin{split}A = \begin{vmatrix} 1 & 1 \\ -1 & 1 \\ \end{vmatrix}\end{split}\]

En el caso considerado se cumpliría \(area(A')=2area(A)\), o equivalentemente \(area(A)=\frac{1}{2}area(A')\). Se podría comprobar que estas relaciones se cumplirían para cualquier región rectangular \(A\), y en particular, tomando elementos diferenciales se obtendría:

\[dA = dx\,dy=\frac{1}{2} du\,dv\]

De igual manera, para todo cambio lineal \(x=au+bv\), \(y=cu+dv\) se tendría

\[\begin{split}dx\,dy=\left|D\right|du\,dv\;\mbox{ donde }\; D=\begin{vmatrix} a & b \\ c & d \\ \end{vmatrix}\end{split}\]

En el caso de que los cambios a aplicar sobre las variables no sean lineales, se puede tener en cuenta que para variaciones infinitesimales toda función puede aproximarse por una función lineal. De esta forma, si se realiza un cambio

\[x = x(u,v)\]

\[y = y(u,v)\]

se tendría en cuenta que

\[dx = x_u du + x_v dv\]

\[dy = y_u du + y_v dv\]

o en forma matricial

\[\begin{split}\left( \begin{array}{c} dx \\ dy \\ \end{array} \right) = \left( \begin{array}{cc} x_u & x_v \\ y_u & y_v \\ \end{array} \right) \left( \begin{array}{c} du \\ dv \\ \end{array} \right)\end{split}\]

donde \(x_u=\frac{\partial x}{\partial u}\), \(x_v=\frac{\partial x}{\partial v}\), \(y_u=\frac{\partial y}{\partial u}\) y \(y_v=\frac{\partial y}{\partial v}\).

Las áreas de los elementos diferenciales \(dA\) se podrían entonces expresar de la siguiente forma:

\[\begin{split}dA=dx\,dy= \left| D \right| du\,dv \;\mbox{ donde }\; D= \left| \begin{array}{cc} x_u & x_v \\ y_u & y_v \\ \end{array} \right|\end{split}\]

Obsérvese que al estar refiriéndose a elementos diferenciales de área, los valores deben ser positivos y por eso se toma el valor absoluto del determinate \(D\).

Con objeto de formalizar todos estos análisis en un resultado de carácter general, en primer lugar se define el concepto de Jacobiano de un cambio de variable:

Jacobiano de un cambio de variable:

Dada una aplicación biyectiva que define un cambio de variable \((x(u,v),y(u,v))\), se define el Jacobiano de ese cambio como el determinante \(J\) de la matriz Jacobiana

\[\begin{split}\frac{\partial(x,y)}{\partial(u,v)}= \left( \begin{array}{cc} x_u & x_v \\ y_u & y_v \\ \end{array} \right)\end{split}\]

Es decir

\[J=det\left(\frac{\partial(x,y)}{\partial(u,v)}\right)\]

A partir de esta definición se pueden establecer relaciones entre los elementos diferenciales de área en las coordenadas \((x,y)\) y \((u,v)\):

\[dx\,dy = \left| \frac{\partial(x,y)}{\partial(u,v)} \right| du\,dv\]

\[du\,dv = \left| \frac{\partial(u,v)}{\partial(x,y)} \right| dx\,dy\]

verificándose además la relación:

\[\left| \frac{\partial(x,y)}{\partial(u,v)} \right|\, \left| \frac{\partial(u,v)}{\partial(x,y)} \right|=1\]

Introducido el concepto de Jacobiano, el siguiente resultado establece el procedimiento para realizar un cambio de variable en una integral doble

Teorema del cambio de variable:

Dada una función \(f(x,y)\) integrable sobre una región \(D\), y \(T:D'\rightarrow D\) una aplicación biyectiva dada por \(T(u,v)=(x(u,v),y(u,v))\) y que relaciona la región \(D\) con otra región \(D'\) en el espacio \(uv\), entonces

\[\iint\limits_{D} f(x,y)dxdy=\iint\limits_{D'} f(x(u,v),y(u,v))\,|J|\,dudv\]

El caso de integración en coordenadas polares no es más que un caso particular de cambio de variables. Si se tiene en cuenta que el cambio viene dado por

\[x=r\cos\theta\;\;\;\;y=r\sin\theta\]

el Jacobiano de dicho cambio es

\[\begin{split}\left| \frac{\partial(x,y)}{\partial(r,\theta)} \right|= \left| \begin{array}{cc} x_r & x_\theta \\ y_r & y_\theta \\ \end{array} \right|= \left| \begin{array}{cc} \cos\theta & -r\sin\theta \\ \sin\theta & r\cos\theta \\ \end{array} \right| = r\cos^2\theta + r\sin^2\theta =r\end{split}\]

Por tanto, para el paso a coordenadas polares \(dxdy=rdrd\theta\), ya que por definición siempre \(r\geq0\).

A continuación se incluyen dos ejemplos adicionales en los que se muestra cómo un cambio de variables convenientemente elegido puede simplificar la resolución de la integral.

---

Ejemplo:

Considérese la integral

\[\iint\limits_{R} xy\,dxdy\]

siendo \(R\) la región dentro del primer cuadrante determinada por \(x^2+2y^2\leq 8\).

import sympy as sp
x,y = sp.symbols('x y')
sp.plot_implicit(sp.And(x**2+2*y**2<=8, x>=0, y>=0), (x,0, 3), (y, 0, 3));

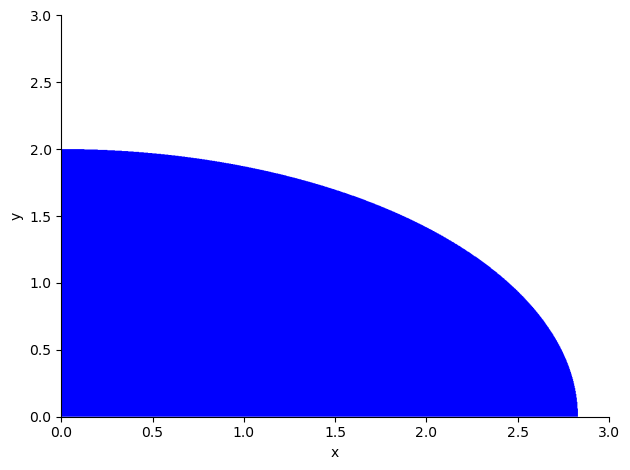
En este caso la función a integrar es muy simple, pero la región de integración podría simplificarse con un cambio de variable.

La condición \(x^2+2y^2\leq 8\) define una elipse que puede expresarse de forma equivalente como

\[\left(\frac{x}{\sqrt{8}}\right)^2+\left(\frac{y}{2}\right)^2\leq 1\]

A la vista de esta expresión, con los cambios \(u=x/\sqrt{8}\), \(v=y/2\) esa región se convertiría en el círculo de centro \((0,0)\) y radio 1, es decir \(u^2+v^2\leq 1\).

Si se tiene en cuenta además que el conjunto inicial estaba en el primer cuadrante (\(x,y\geq 0\)), las nuevas variables \(u\) y \(v\) también deberían cumplir \(u,v\geq 0\).

Respecto al Jacobiano del cambio de variables, se necesitaría en primer lugar obtener las funciones \(x(u,v)\) e \(y(u,v)\), que en este caso resultan

\[x=\sqrt{8}u;\;\;\;\;y=2v\]

con lo que

\[\begin{split}\left| \frac{\partial(x,y)}{\partial(u,v)} \right|= \left| \begin{array}{cc} \sqrt{8} & 0 \\ 0 & 2 \\ \end{array} \right| = 2\sqrt{8}\end{split}\]

De acuerdo al teorema del cambio de variable, la integral resultante sería

\[\iint\limits_{u^2+v^2\leq 1;\;u\geq 0;\; v\geq 0} \sqrt{8}u\,2v\, 2\sqrt{8}\,dudv= 32\iint\limits_{u^2+v^2\leq 1;\;u\geq 0;\; v\geq 0} uv\,dudv\]

Esta integral puede resolverse con un nuevo cambio de variables, en este caso pasando a coordenadas polares, es decir, \(u=r\cos\theta\) y \(v=r\sin\theta\)

\[32\int_0^{\pi/2}\int_0^1 r^2\cos\theta\sin\theta\,r\,drd\theta= 32\int_0^{\pi/2}\frac{1}{4} \cos\theta\sin\theta\,d\theta= \left.8\frac{\sin^2\theta}{2} \right|_0^{\pi/2}= 4\]

---

Ejemplo:

En este ejemplo se considera la integral

\[\iint\limits_{R} e^{xy}\,dxdy\]

siendo \(R\) la región que viene delimitada por las siguientes restricciones:

\[ y \geq x; \;\; y \leq 2x; \;\; xy \geq 1; \;\; xy \leq 2 \]

x,y = sp.symbols('x y')
sp.plot_implicit(sp.And(y>=x, y<=2*x, x*y>=1, x*y<=2), (x,0,2), (y,0,2));

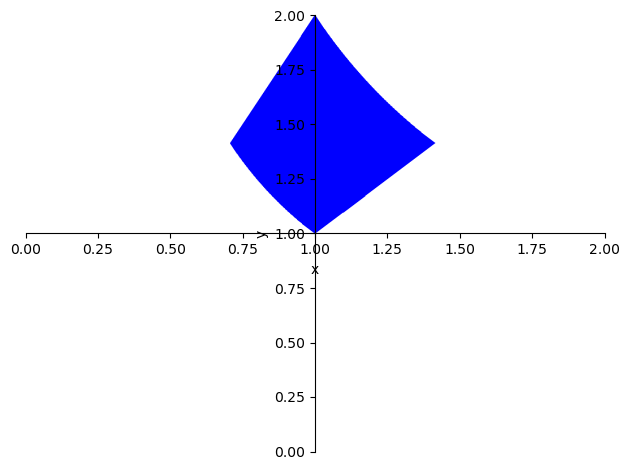
A la vista de estas restricciones, un cambio de variable que podría simplificar el recinto de integración es

\[u=xy;\;\;\;\;v=\frac{y}{x}\]

Con ese cambio el recinto de integración \(R\) se transformaría en \(R'=[1,2]\times[1,2]\) en el espacio \(uv\)

Para poder aplicar ese cambio sobre la integral se necesita obtener el cambio inverso \(x=x(u,v);\,y=y(u,v)\).

\[\frac{u}{v}=x^2 \Rightarrow x=\sqrt{\frac{u}{v}}\]

\[uv=y^2 \Rightarrow y=\sqrt{uv}\]

El siguiente paso es el cálculo del Jacobiano:

\[\begin{split}J= \left| \begin{array}{cc} \frac{1/v}{2\sqrt{u/v}} & \frac{-u/v^2}{2\sqrt{u/v}} \\ \frac{v}{2\sqrt{uv}} & \frac{u}{2\sqrt{uv}} \\ \end{array} \right| =\frac{1}{2v}\end{split}\]

Como en el nuevo recinto de integración \(R'\) la variable \(v\) siempre toma valores positivos, \(|J|=1/2v\). Aplicando el cambio de variable, la integral se transforma en:

\[\iint\limits_{R'} e^{u}\,\frac{1}{2v}dudv= \int_1^2\left( \int_1^2 e^{u}\,\frac{1}{2v}du \right)dv\]

La integral interior es:

\[\int_1^2 e^{u}\,\frac{1}{2v}du= \left.\frac{e^{u}}{2v}\right|_{u=1}^{u=2}= \frac{e^2-e}{2v}\]

y la integral exterior resulta:

\[\int_1^2 \frac{e^2-e}{2v} dv= \left.\frac{e^2-e}{2}\ln v\right|_{v=1}^{v=2}=\frac{e^2-e}{2}\ln 2\]

Todo este proceso de aplicación del cambio de variable podría realizarse con diferentes funciones que se encuentran implementadas en el paquete SymPy de Numpy.

x,y,u,v = sp.symbols('x,y,u,v')
F = sp.exp(x*y)
xuv = sp.sqrt(u/v)
yuv = sp.sqrt(u*v)
Jacobiana = sp.Matrix([[sp.diff(xuv,u),sp.diff(xuv,v)],
                       [sp.diff(yuv,u),sp.diff(yuv,v)]])
Jacobiana

\[\begin{split}\displaystyle \left[\begin{matrix}\frac{\sqrt{\frac{u}{v}}}{2 u} & - \frac{\sqrt{\frac{u}{v}}}{2 v}\\\frac{\sqrt{u v}}{2 u} & \frac{\sqrt{u v}}{2 v}\end{matrix}\right]\end{split}\]

J = Jacobiana.det().simplify()
J

\[\displaystyle \frac{\sqrt{\frac{u}{v}} \sqrt{u v}}{2 u v}\]

Fcambio = F.subs({x:xuv,y:yuv})
Fcambio

\[\displaystyle e^{\sqrt{\frac{u}{v}} \sqrt{u v}}\]

sp.integrate(Fcambio * J, (u, 1, 2), (v, 1, 2))

\[\displaystyle \left(- \frac{e}{2} + \frac{e^{2}}{2}\right) \log{\left(2 \right)}\]

Ejercicios propuestos

• Calcular \(\iint\limits_{R} f(x,y)dA\) siendo \(R\) la región dentro del círculo de radio 1 y centro \((0,0)\), y \(f(x,y)=\frac{1}{\sqrt{x^2+y^2}}\).

• Calcular \(\iint\limits_{R} (x+y)dA\) siendo \(R\) la región del primer cuadrante dentro del círculo \(x^2+y^2\leq a^2\), y por debajo de la recta \(y=x\sqrt{3}\).

• Calcular el área que queda encerrado dentro de la curva cardiode: \(r = 1+\cos\theta\) y de la rosa de cuatro pétalos: \(r=a\sin 2\theta\)

• Dada la integral \(\iint\limits_{R} (xy^2+2y)dA\) siendo \(R\) el paralelogramo determinado por los puntos \((1,1)\), \((4,1)\), \((0,3)\) y \((3,3)\), buscar un cambio de variable que transforme \(R\) en el cuadrado unidad \([0,1]\times[0,1]\) y posteriormente resolver la integral aplicando ese cambio.

• Expresar la integral \(\int_0^1\left( \int_0^{x^2} xy\,dy \right)dx\) como una integral sobre el triángulo definido por las restricciones \(0\leq u\leq 1\) y \(0\leq v\leq u\), y posteriormente calcular la integral de las dos formas, comprobando que se obtiene el mismo resultado.