Aplicaciones prácticas de la integración doble

La integración doble tiene un gran número de aplicaciones prácticas en la física y la ingeniería. En la sección previa ya se han analizado algunas aplicaciones relacionadas con el cálculo de áreas y volúmenes, pero también hay aplicaciones físicas como el cálculo de masas, centros de masas, momentos estáticos y momentos de inercia para regiones bidimensionales.

Cálculo de áreas y volúmenes

En las secciones previas se ha visto cómo una integral doble permite calcular el volumen del sólido que se genera sobre una determinada región de integración plana \(R\) y por debajo de la superficie \(z=f(x,y)\) definida por la función \(f(x,y)\). En el caso particular de \(f(x,y)=1\) ese volumen coincide con el área de la región \(R\). Por tanto:

\[Area(R)=\iint\limits_RdA\]

---

Ejemplo:

Considérese la región \(R\) definida por las dos condiciones \(y\geq x^2-1\) e \(y \leq 5-x^2\). Para calcular su área resulta conveniente visualizar la forma del recinto.

import sympy as sp
x,y = sp.symbols('x,y')
y1 = x**2 -1 
y2 = 5-x**2
sp.plot(y1, y2, xlim=[-3,3], ylim=[-3,5]);

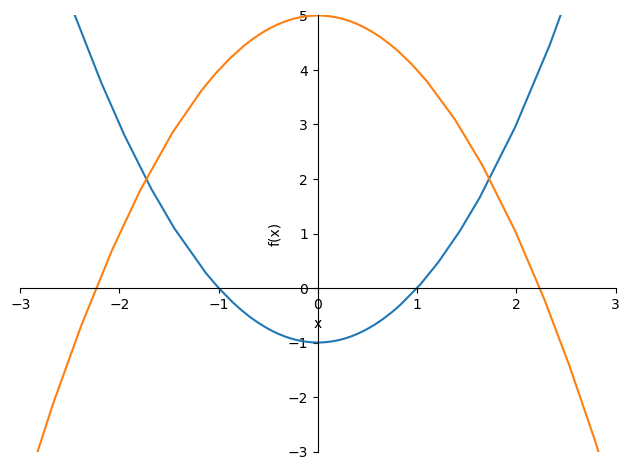
Es necesario determinar los puntos de intersección entre ambas parábolas, de manera que en el recinto de integración la variable \(x\) variaría entre esos dos puntos y la variable \(y\) entre \(x^2-1\) y \(5-x^2\).

sp.solve(y1-y2)

[-sqrt(3), sqrt(3)]

El área del recinto se calcularía mediante la siguiente integral doble:

\[Area(R) = \iint\limits_RdA= \int_{-\sqrt{3}}^{\sqrt{3}}\left( \int_{x^2-1}^{5-x^2} dy \right)dx = \int_{-\sqrt{3}}^{\sqrt{3}}\left( (5-x^2)-(x^2-1) \right)dx \]

\[= \left. 6x-2\frac{x^3}{3} \right|_{-\sqrt{3}}^{\sqrt{3}} =8\sqrt{3}\]

Se puede comprabar el valor de la integral con Python:

sp.integrate(1, (y, y1, y2), (x, -sp.sqrt(3), sp.sqrt(3)))

\[\displaystyle 8 \sqrt{3}\]

---

La integral doble define el volumen debajo de la superficie que determina la función, pero también es posible utilizar integrales dobles para determinar el volumen del sólido en en el espacio acotado por dos superficies.

Si \(f(x,y)\) y \(g(x,y)\) son dos funciones continuas en una región bidimensional \(R\), cumpliendo \(f(x,y)\leq g(x,y)\) \(\forall (x,y)\in R\), entonces el volumen del sólido sobre \(R\) acotado superiormente por la superficie \(z=g(x,y)\) e inferiormente por la superficie \(z=f(x,y)\) es:

\[ Volumen=\iint\limits_R(g(x,y)-f(x,y))dA \]

---

Ejemplo:

Dadas las funciones \(g(x,y)=6-\frac{x^2+y^2}{4}\) y \(f(x,y)=\frac{x^2+y^2}{2}\) el sólido que se forma entre las dos superficies \(z=g(x,y)\) y \(z=f(x,y)\) puede visualizarse de la siguiente manera

import matplotlib.pyplot as plt
import numpy as np
x, y = np.meshgrid(np.linspace(-3, 3, 100), np.linspace(-3, 3, 100))
z1 = 6-(x**2+y**2)/4
z2 = (x**2+y**2)/2
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
ax.plot_surface(x, y, z1, alpha=0.5, cmap='viridis')
ax.plot_surface(x, y, z2, alpha=0.5, cmap='plasma')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Volumen entre dos superficies')
plt.show()

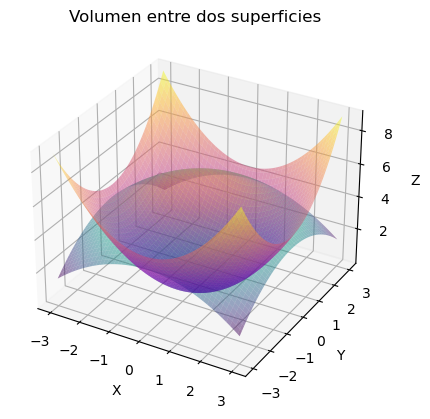
Si se quisiera calcular el volumen de ese sólido en primer lugar habría que determinar la proyección sobre el plano de la curva de corte entre ambas superficies. Para ello habría que considerar la ecuación

\[f(x,y)=g(x,y) \Leftrightarrow \frac{x^2+y^2}{2}=6-\frac{x^2+y^2}{4} \Leftrightarrow x^2+y^2=8\]

La región de integración \(R\) sería por tanto el círculo de centro \((0,0)\) y radio \(\sqrt{8}\), y para calcular el volumen del sólido habría que resolver la siguiente integral:

\[Volumen=\iint\limits_R(g(x,y)-f(x,y))dA=\iint\limits_R\left(6-\frac{3}{4}(x^2+y^2) \right) dxdy\]

Para resolver esa integral es recomendable realizar un cambio a coordenadas polares \(x=r\cos\theta\) e \(y=r\sin\theta\), obteniéndose:

\[ Volumen = \int_0^{\sqrt{8}} \left( \int_0^{2\pi} \left(6-\frac{3}{4}r^2\right)r\,d\theta \right)dr\]

\[ = \int_0^{\sqrt{8}} \left(6r-\frac{3}{4}r^3\right)2\pi\,dr = \left. 3r^2-\frac{3}{16}r^4 \right|_0^{\sqrt{8}} =24\pi \]

Se comprueba igualmente el valor de esa integral con Python:

r,t = sp.symbols('r,t')
Jacobiano = r
sp.integrate((6-3*r**2/4)*r, (t,0,2*sp.pi), (r,0,sp.sqrt(8)))

\[\displaystyle 24 \pi\]

Masas de láminas planas y cálculo de centros de masa

Si se tiene una lámina plana cuya forma viene dada por una región \(R\) en el plano y la densidad de la lámina es una función \(\delta(x,y)\), la integración doble también permite calcular la masa de la lámina. Dado un elemento de área \(\Delta A\), su masa sería \(\Delta m=\delta \Delta A\), y la masa total se obtendría sumando todos los elementos diferenciales de masa. En definitiva, la masa de la lámina viene dada por:

\[masa(R)=\iint\limits_R\delta(x,y)dA\]

En el caso de densidad constante \(\delta(x,y)=\delta\), se dice que la lámina es homogénea, pero en general la densidad podría variar de unos puntos a otros de la lámina.

Otro concepto que puede ser calculado a partir de la integral es el del centro de masas, para ello se necesita calcular en primer lugar los momentos estáticos. El momento estático de una partícula alrededor de un eje es el producto de su masa por la distancia a ese eje. En el caso de una lámina plana, se tendría que hacer una suma de los momentos de todas sus partículas, por lo que los momentos estáticos alrededor de los ejes \(OX\) y \(OY\) serían:

\[M_x =\iint\limits_R y\delta(x,y)dA; \;\;\;\;\;\;M_y =\iint\limits_R x\delta(x,y)dA \]

A partir de esos momentos, el centro de masa de la lámina sería el punto \((\bar{x},\bar{y})\) definido a partir de las siguientes expresiones:

\[\bar{x} = \frac{M_y}{masa(R)} = \frac{\iint\limits_R x\delta(x,y)dA}{\iint\limits_R \delta(x,y)dA};\;\;\;\;\;\ \bar{y} = \frac{M_x}{masa(R)} = \frac{\iint\limits_R y\delta(x,y)dA}{\iint\limits_R \delta(x,y)dA}\]

Las ecuaciones anteriores pueden verse como los valores promedios de las variables \(x\) e \(y\), respectivamente, ponderados por la función de densidad sobre todos los puntos de la lámina \(R\).

---

Ejemplo:

Considérese una lámina plana de densidad variable de forma triangular y delimitada por los puntos \((0,0)\), \((0,3)\) y \((2,3)\), siendo la función de densidad \(\delta(x,y)=2x+y\).

x = np.array([0, 0, 2])
y = np.array([0, 3, 3])
fig, ax = plt.subplots()
ax.axis('equal')
ax.fill(x, y, color='blue') 
ax.set_title('Lámina de densidad variable')
plt.show()

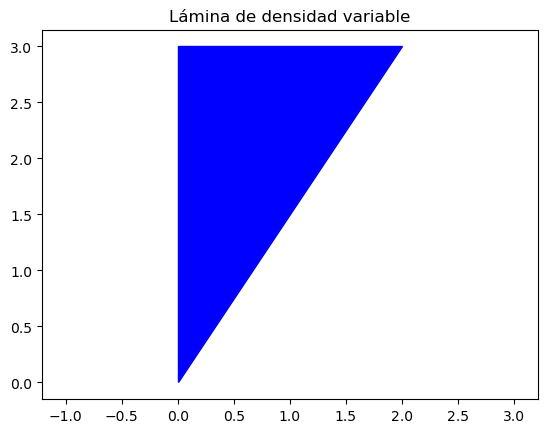
Teniendo en cuenta los vértices que determinan el triángulo, puede observarse cómo el valor de \(x\) varía dentro del intervalo \([0,2]\), y para un valor fijo de \(x\) la coordenada \(y\) varía entre \(3x/2\) y \(3\). Teniendo en cuenta esto, la masa de la lámina sería:

\[masa(R) = \iint\limits_R\delta(x,y)dA= \int_{0}^{2}\left( \int_{3x/2}^{3}(2x+y)dy \right)dx \]

\[ = \int_0^2 (6x+\frac{9}{2}-3x^2-\frac{9}{8}x^2)dx =10\]

Para calcular el centro de masas se calculan previamente los momentos estáticos \(M_x\) y \(M_y\):

\[M_x = \iint\limits_R y\delta(x,y)dA= \int_{0}^{2}\left( \int_{3x/2}^{3}(2xy+y^2)dy \right)dx =\frac{45}{2}\]

\[M_y = \iint\limits_R x\delta(x,y)dA= \int_{0}^{2}\left( \int_{3x/2}^{3}(2x^2+xy)dy \right)dx=\frac{17}{2}\]

El centro de masas de la lámina \(R\) sería entonces el punto:

\[\bar{x} = \frac{M_y}{masa(R)} =\frac{17/2}{10} =\frac{17}{20}\]

\[\bar{y} = \frac{M_x}{masa(R)} =\frac{45/2}{10} =\frac{45}{20}\]

De nuevo, todas estas operaciones pueden realizarse con las funciones de integración del paquete SymPy:

x,y = sp.symbols('x,y')
densidad = 2*x+y
masa = sp.integrate(densidad, (y,3*x/2,3), (x,0,2))
cx = sp.integrate(x*densidad, (y,3*x/2,3), (x,0,2))/masa
cy = sp.integrate(y*densidad, (y,3*x/2,3), (x,0,2))/masa
print('Centro de masas:',cx,cy)

Centro de masas: 17/20 9/4

---

Valores promedios de una función sobre un recinto

En general, el promedio de una función \(f(x,y)\) sobre \(R\) es

\[\bar{f}=\frac{1}{area(R)}\iint\limits_R f(x,y)dA\]

Esta expresión puede ser utilizada, por ejemplo, para calcular el valor medio de una temperatura que varía en los disitintos puntos del plano.

---

Ejemplo:

En un recinto rectangular \([0,4]\times[0,3]\) la temperatura medida en un punto \((x,y)\) viene dada por la función \(T(x,y)=20x^{0.3}y^{0.4}\), si se desea calcular el valor medio de la temperatura, se debería realizar la siguiente integración doble.

x,y = sp.symbols('x,y')
T = 20 * x**0.3 * y**0.4
area = sp.integrate(1, (x,0,4), (y,0,3))
Tmedia = (1/area)*sp.integrate(T, (x,0,4), (y,0,3))
Tmedia

\[\displaystyle 25.8478906049379\]

Momentos de inercia

El momento de inercia es una medida de la oposición a girar del cuerpo cuando actúa sobre él una fuerza de rotación. El momento de inercia de una partícula alrededor de un eje se define como el producto de su masa por el cuadrado de la distancia que la separa de ese eje. En el caso de un cuerpo plano, sus momentos de inercia alrededor de los ejes coordenados pueden calcularse con sendas integrales dobles:

\[I_x =\iint\limits_R y^2\delta(x,y)dA,\;\;\;\;\;\;\;\;I_y =\iint\limits_R x^2\delta(x,y)dA\]

En el caso concreto de que se considere un giro alrededor del origen el momento de inercia, conocido también como momento de inercia polar, se calcularía mediante la expresión

\[I_0 =\iint\limits_R (x^2+y^2)\delta(x,y)dA\]

Obsérvese que hay una relación obvia entre el momento de inercia polar y los momentos con respecto a los ejes: \(I_0=I_x+I_y\)

---

Ejemplo:

Dado el cuadrado unidad \(R=[0,1]\times[0,1]\) con densidad \(\delta(x,y)=xy\), para el cálculo de los momentos de inercia respecto a los ejes coordenados habría que resolver las siguientes integrales:

\[ I_x = \iint\limits_R xy^3\,dA=\int_0^1\int_0^1 xy^3\,dy\,dx =\frac{1}{8}\]

\[ I_y = \iint\limits_R x^3y\,dA=\int_0^1\int_0^1 x^3y\,dy\,dx =\frac{1}{8}\]

Como puede apreciarse, la total simetría de la región \(R\) y de la función de densidad hace que los momentos de inercia con respecto a ambos ejes sean iguales.

Para calcular el momento de inercia polar, es decir la medida de la oposición del cuerpo a girar en torno al origen, se debería resolver la siguiente integral:

\[I_0 =\iint\limits_R (x^2+y^2)xy\,dA=\int_0^1\int_0^1 (x^3y+xy^3)\,dy\,dx=I_x+I_y=\frac{1}{4}\]

x,y = sp.symbols('x,y')
densidad = x*y
Ix = sp.integrate(y**2*densidad, (x,0,1), (y,0,1))
Iy = sp.integrate(x**2*densidad, (x,0,1), (y,0,1))
print('Momentos de inercia:', Ix, Iy)

Momentos de inercia: 1/8 1/8

Ejercicios propuestos

• Calcular el área de la región plana que viene delimitada por las condiciones \(y\geq 4x^2\), \(y\leq 16x+20\) e \(y\leq -2x+20\).

• Calcular el volumen del sólido acotado por las superficies \(z=1\) y \(z=4+xy\) dentro del cilindro \(x^2+y^2\leq 1\).

• Determinar la masa y el centro de masas de la lámina plana limitada por las curvas \(x=y^2-1\) y \(x=2y^2-2\), asumiendo una densidad homogénea igual a la unidad.

• Determinar el centro de masas de una lámina semicircular que cumple que la densidad en cualquier punto es proporcional a la distancia al centro del círculo.

• Sea \(R\) el triángulo con vértices en los puntos \((0,0)\), \((1,0)\) y \((1,\sqrt{3})\), y considérese una densidad homogénea \(\delta = 1\). Calcular el momento de inercia polar del triángulo.