Cambios de variable en integrales triples: coordenadas cilíndricas y esféricas

Al igual que ocurría en la integración doble, en ocasiones un cambio de variables puede simplificar la resolución de una integral triple. A continuación se presenta el esquema general para la aplicación de un cambio de variable, para pasar posteriormente a analizar los casos particulares de dos tipos de cambios de variable comunes a la hora de resolver diferentes integrales triples.

Cambio de variable en integrales triples:

Dada una función \(f(x,y,z)\) integrable sobre una región \(R\), y \(T:R'\rightarrow R\) una aplicación biyectiva dada por \(T(u,v,w)=(x(u,v,w),y(u,v,w),z(u,v,w))\) que relaciona la región \(R\) con otra región \(R'\), asumiendo que las funciones que definen el cambio son derivables y con derivada continua en \(R'\) y que el jacobiano de la aplicación es no nulo, es decir:

\[\begin{split}J=det\left(\frac{\partial(x,y,z)}{\partial(u,v,v)}\right)= \left| \begin{array}{ccc} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} & \frac{\partial x}{\partial w} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} & \frac{\partial y}{\partial w} \\ \frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} & \frac{\partial z}{\partial w} \end{array} \right|\neq 0\end{split}\]

entonces

\[\iiint\limits_{R} f(x,y,z)dx\,dy\,dz= \iiint\limits_{R'} f(x(u,v,w),y(u,v,w),z(u,v,w))\,|J|\,du\,dv\,dw\]

Integración en coordenadas cilíndricas

Las coordenadas cilíndricas vienen determinadas por el siguiente cambio de variables:

\[ x = r\cos\theta \]

\[ y = r\sin\theta \]

\[ z = z \]

El jacobiano de este cambio de coordenadas es:

\[\begin{split}J=det\left(\frac{\partial(x,y,z)}{\partial(r,\theta,z)}\right)= \left| \begin{array}{ccc} \cos\theta & -r\sin\theta & 0 \\ \sin\theta & r\cos\theta & 0 \\ 0 & 0 & 1 \end{array} \right| = r\end{split}\]

import sympy as sp
x,y,z,r,theta = sp.symbols('x,y,z,r,theta')
x = r*sp.cos(theta)
y = r*sp.sin(theta)
z = z
Jacobiana = sp.Matrix([[sp.diff(x,r),sp.diff(x,theta),sp.diff(x,z)],
                       [sp.diff(y,r),sp.diff(y,theta),sp.diff(y,z)],
                       [sp.diff(z,r),sp.diff(z,theta),sp.diff(z,z)]])
Jacobiana

\[\begin{split}\displaystyle \left[\begin{matrix}\cos{\left(\theta \right)} & - r \sin{\left(\theta \right)} & 0\\\sin{\left(\theta \right)} & r \cos{\left(\theta \right)} & 0\\0 & 0 & 1\end{matrix}\right]\end{split}\]

Jacobiana.det().simplify()

\[\displaystyle r\]

La interpretación de este nuevo sistema de coordenadas puede verse en la siguiente figura

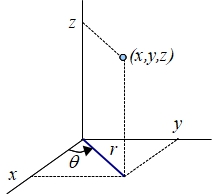
Y el cambio inverso que relaciona las coordenadas cilíndricas y cartesianas es

\[r=\sqrt{x^2+y^2}\]

\[\theta=arctg\left(\frac{y}{x}\right)\]

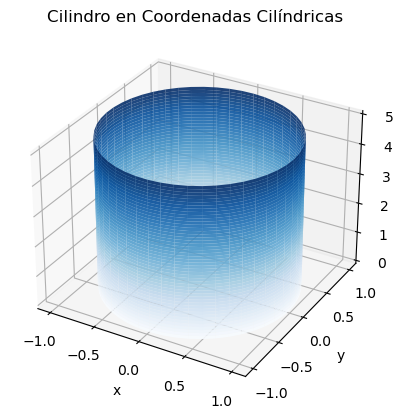
Las coordenadas cilíndricas permiten representar fácilmente superficies cilíndricas, tal como se comprueba en la siguiente representación:

import matplotlib.pyplot as plt
import numpy as np
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})

# Parámetros para el cilindro
radio, altura = 1, 5
theta, z = np.meshgrid(np.linspace(0, 2*np.pi), np.linspace(0, altura))
# Coordenadas cartesianas
x, y, z = radio*np.cos(theta), radio*np.sin(theta), z

ax.set_title('Cilindro en Coordenadas Cilíndricas')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.plot_surface(x, y, z, cmap='Blues', alpha=0.9)
plt.show()

---

Ejemplo:

Dada la integral

\[\iiint_R dV\]

siendo \(R\) el sólido delimitado por las superficies \(z=4-x^2-y^2\) y \(z=x^2+y^2\), el uso de coordenadas cilíndricas facilita su cálculo. En primer lugar puede ser interesante realizar una representación gráfica del recinto de integración:

fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
ax.set_title('Recinto de integración')
ax.set_xlabel('x'); ax.set_ylabel('y'); ax.set_zlabel('z')
x, y = np.meshgrid(np.linspace(-2, 2), np.linspace(-2, 2))
z1 = 4-x**2-y**2
z2 = x**2+y**2
ax.plot_surface(x, y, z1, alpha=0.5, cmap='viridis')
ax.plot_surface(x, y, z2, alpha=0.5, cmap='BuPu')
plt.show()

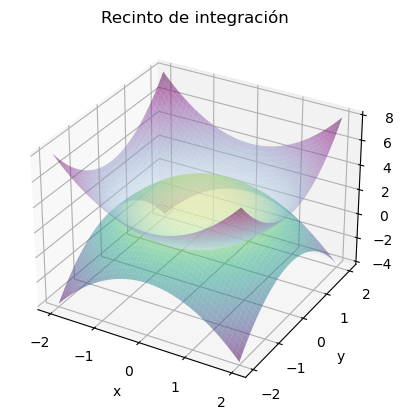
El siguiente paso es identificar cuál es la proyección del sólido sobre el plano \(OXY\). Teniendo en cuenta que la intersección de ambas superficies es

\[4-x^2-y^2 = x^2+y^2 \Longleftrightarrow x^2+y^2 = 2\]

dicha proyección sería un círculo de centro \((0,0)\) y radio \(\sqrt{2}\). Dado un punto \((x,y)\) en dicho círculo, el valor de la variable \(z\) en el sólido variará en el intervalo definido por

\[4-x^2-y^2\leq z\leq x^2+y^2\]

Usando coordenadas cilíndricas, \(x=r\cos\theta\), \(y=r\sin\theta\), \(x^2+y^2=r^2\), por lo que la integral se reduce a

\[I=\int_{0}^{2\pi}\int_{0}^{\sqrt{2}}\int_{r^2}^{4-r^2}r\,dz\,dr\,d\theta\]

Realizando las integrales iteradas se obtiene:

\[I=\int_{0}^{2\pi}\int_{0}^{\sqrt{2}}(4r-2r^3)\,dr\,d\theta= \int_{0}^{2\pi} 2\,d\theta=4\pi\]

El proceso completo de integración en coordenadas cilíndricas se podría realizar también con Python, aunque obviamente, la determinación de los intervalos de variación de los parámetros debe ser realizado de manera manual

import sympy as sp
x,y,z,r,theta = sp.symbols('x,y,z,r,theta')
x = r*sp.cos(theta)
y = r*sp.sin(theta)
z = z
J = sp.Matrix([[sp.diff(x,r),sp.diff(x,theta),sp.diff(x,z)],
               [sp.diff(y,r),sp.diff(y,theta),sp.diff(y,z)],
               [sp.diff(z,r),sp.diff(z,theta),sp.diff(z,z)]]).det()
F = 1
sp.integrate(F*J, (z,r**2,4-r**2), (r,0,sp.sqrt(2)), (theta,0,2*sp.pi))

\[\displaystyle 4 \pi\]

---

Ejemplo:

En este nuevo ejemplo se calcula la integral

\[\iiint_R (2xy+z^2)dV\]

siendo \(R\) la parte del cilindro \(x^2+y^2\leq 9\) que está dentro del primer octante (\(x,y,z\geq 0\)) y además \(z\leq 5\). El sólido es el encerrado por las superficies que se muestran en la siguiente figura:

fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
ax.set_title('Recinto de integración')
ax.set_xlabel('x'); ax.set_ylabel('y'); ax.set_zlabel('z')
# superficie lateral curva
theta, z = np.meshgrid(np.linspace(0, np.pi/2), np.linspace(0, 5))
r = 3
ax.plot_surface(r*np.cos(theta), r*np.sin(theta), z, alpha=0.5, cmap='Blues')
# planos verticales
a, z = np.meshgrid(np.linspace(0, 3), np.linspace(0, 5))
ax.plot_surface(0, a, z, alpha=0.5, cmap='Blues')
ax.plot_surface(a, 0, z, alpha=0.5, cmap='Blues')
# planos horizontales
r, theta = np.meshgrid(np.linspace(0, 3), np.linspace(0, np.pi/2))
ax.plot_surface(r*np.cos(theta), r*np.sin(theta), 5*np.ones_like(r), alpha=0.5, cmap='viridis')
ax.plot_surface(r*np.cos(theta), r*np.sin(theta), np.zeros_like(r), alpha=0.5, cmap='viridis')
plt.show()

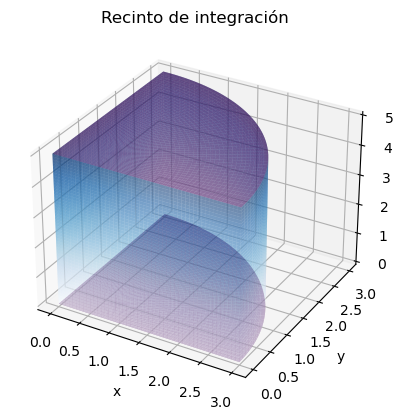
La integral triple implicaría el cálculo de las siguientes integrales iteradas:

\[I=\int_{0}^{5}\int_{0}^{\pi/2}\int_{0}^{3}(2r\cos\theta\; r\sin\theta+z^2)r\,dr\,d\theta\,dz\]

Es importante no olvidar de introducir el jacobiano como factor multiplicativo en la función a integrar. En el caso del cambio a coordenadas cilíndricas el jacobiano es \(r\).

El proceso completo de integración en coordenadas polares con Python sería el siguiente:

x,y,z,r,theta = sp.symbols('x,y,z,r,theta')
x = r*sp.cos(theta)
y = r*sp.sin(theta)
z = z
J = sp.Matrix([[sp.diff(x,r),sp.diff(x,theta),sp.diff(x,z)],
               [sp.diff(y,r),sp.diff(y,theta),sp.diff(y,z)],
               [sp.diff(z,r),sp.diff(z,theta),sp.diff(z,z)]]).det()
F = 2*x*y + z**2  #al haberse definido el cambio previamente, se aplica de forma directa
sp.integrate(F*J, (r,0,3), (theta,0,sp.pi/2), (z,0,5))

\[\displaystyle \frac{405}{4} + \frac{375 \pi}{4}\]

Integración en coordenadas esféricas

Otro sistema de coordenadas que puede facilitar la resolución de determinadas integrales triples es el de coordenadas esféricas. En este caso el cambio viene definido por las relaciones:

\[ x = r\sin\phi\cos\theta \]

\[ y = r\sin\phi\sin\theta \]

\[ z = r\cos\phi \]

El jacobiano de este cambio es:

\[\begin{split}J=det\left(\frac{\partial(x,y,z)}{\partial(r,\phi,\theta)}\right)= \left| \begin{array}{ccc} \sin\phi\cos\theta & r\cos\phi\cos\theta & -r\sin\phi\sin\theta \\ \sin\phi\sin\theta & r\cos\phi\sin\theta & r\sin\phi\cos\theta \\ \cos\phi & -r\sin\phi & 0 \end{array} \right| = r^2\sin\phi\end{split}\]

import sympy as sp
x,y,z,r,phi,theta = sp.symbols('x,y,z,r,phi,theta')
x = r*sp.sin(phi)*sp.cos(theta)
y = r*sp.sin(phi)*sp.sin(theta)
z = r*sp.cos(phi)
Jacobiana = sp.Matrix([[sp.diff(x,r),sp.diff(x,phi),sp.diff(x,theta)],
                       [sp.diff(y,r),sp.diff(y,phi),sp.diff(y,theta)],
                       [sp.diff(z,r),sp.diff(z,phi),sp.diff(z,theta)]])
Jacobiana

\[\begin{split}\displaystyle \left[\begin{matrix}\sin{\left(\phi \right)} \cos{\left(\theta \right)} & r \cos{\left(\phi \right)} \cos{\left(\theta \right)} & - r \sin{\left(\phi \right)} \sin{\left(\theta \right)}\\\sin{\left(\phi \right)} \sin{\left(\theta \right)} & r \sin{\left(\theta \right)} \cos{\left(\phi \right)} & r \sin{\left(\phi \right)} \cos{\left(\theta \right)}\\\cos{\left(\phi \right)} & - r \sin{\left(\phi \right)} & 0\end{matrix}\right]\end{split}\]

Jacobiana.det().simplify()

\[\displaystyle r^{2} \sin{\left(\phi \right)}\]

La interpretación del sistema de coordenadas esféricas puede verse en siguiente figura

---

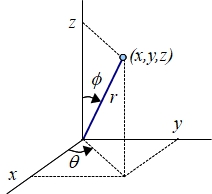
Ejemplo:

Considérese la integral

\[\iiint_R (x^2+y^2)dV\]

siendo \(R\) la parte de la esfera unidad centrada en el origen que queda comprendida dentro del primer octante del espacio. Es decir,

\[R=\left\{(x,y,z)\in R^3\left| x^2+y^2+z^2\leq 1,\;x\geq 0,\;y\geq 0,\;z\geq 0 \right.\right\}\]

Este recinto de integración puede visualizarse fácilmente si se representan las superficies que lo determinan:

fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.set_title('Recinto de integración')
ax.set_xlabel('x'); ax.set_ylabel('y'); ax.set_zlabel('z')
# superficie esférica
phi, theta = np.meshgrid(np.linspace(0, np.pi/2), np.linspace(0, np.pi/2))
r = 1
x = r * np.sin(phi) * np.cos(theta)
y = r * np.sin(phi) * np.sin(theta)
z = r * np.cos(phi)
ax.plot_surface(x, y, z, alpha=0.5, cmap='Blues')
# planos coordenados
r, theta = np.meshgrid(np.linspace(0, 1), np.linspace(0, np.pi/2))
ax.plot_surface(0, r*np.cos(theta), r*np.sin(theta), alpha=0.5, cmap='viridis')
ax.plot_surface(r*np.cos(theta), 0, r*np.sin(theta), alpha=0.5, cmap='viridis')
ax.plot_surface(r*np.cos(theta), r*np.sin(theta), np.zeros_like(r), alpha=0.5, cmap='viridis')
plt.show()

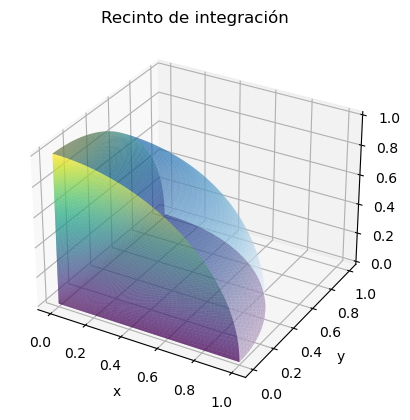
Con el cambio a coordenadas esféricas

\[ x = r\sin\phi\cos\theta \]

\[ y = r\sin\phi\sin\theta \]

\[ z = r\cos\phi \]

los límites de integración de las variables serían:

\[ 0 \leq r \leq 1 \]

\[ 0 \leq \phi \leq \frac{\pi}{2} \]

\[ 0 \leq \theta \leq \frac{\pi}{2} \]

Teniendo en cuenta además el jacobiano del cambio \(J=r^2\sin\phi\), la integral se reduce a

\[ I = \int_{0}^{\pi/2}\int_{0}^{\pi/2}\int_{0}^{1} (r^2\sin^2\phi\cos^2\theta + r^2\sin^2\phi\sin^2\theta) r^2\sin\phi \,dr\,d\phi\,d\theta \]

\[ = \int_{0}^{\pi/2}\int_{0}^{\pi/2}\int_{0}^{1} r^4\sin^3\phi \,dr\,d\phi\,d\theta\]

Tras realizar la integral interior se obtiene

\[I=\int_{0}^{\pi/2}\int_{0}^{\pi/2} \frac{1}{5}\sin^3\phi \,d\phi\,d\theta=\frac{1}{5}\int_{0}^{\pi/2}\int_{0}^{\pi/2} \sin^3\phi \,d\phi\,d\theta\]

La siguiente integral iterada puede resolverse con ayuda de un cambio de variable \(u=\cos\phi\):

\[\int_{0}^{\pi/2} \sin^3\phi\,d\phi=\int_{0}^{\pi/2} \sin\phi(1-\cos^2\phi)\,d\phi =\int_1^0 -(1-u^2)du=\int_0^1 (1-u^2)du=\frac{2}{3}\]

Finalmente la integral triple resulta ser

\[I=\frac{1}{5}\int_{0}^{\pi/2} \frac{2}{3}d\theta=\frac{\pi}{15}\]

De nuevo, todo este proceso puede realizarse con ayuda de las funciones de integración simbólica del paquete SymPy:

x,y,z,r,phi,theta = sp.symbols('x,y,z,r,phi,theta')
x = r*sp.sin(phi)*sp.cos(theta)
y = r*sp.sin(phi)*sp.sin(theta)
z = r*sp.cos(phi)
J = sp.Matrix([[sp.diff(x,r),sp.diff(x,phi),sp.diff(x,theta)],
               [sp.diff(y,r),sp.diff(y,phi),sp.diff(y,theta)],
               [sp.diff(z,r),sp.diff(z,phi),sp.diff(z,theta)]]).det()
F = x**2 + y**2  # al haberse definido el cambio previamente, se aplica de forma directa
sp.integrate(F*J, (r,0,1), (phi,0,sp.pi/2), (theta,0,sp.pi/2))

\[\displaystyle \frac{\pi}{15}\]

Ejercicios propuestos

• Calcular, utilizando coordenadas cilíndricas, la siguiente integral \(\iiint\limits_{R} \sqrt{x^2+y^2}dV\) siendo \(R\) el cono definido por las condiciones \(x^2+y^2\leq z^2\), \(0\leq z\leq 1\).

• Calcular la integral \(\iiint\limits_{R} xyz\,dV\) siendo \(R\) el recinto definido como:

\[R=\left\{ (x,y,z)\in R^3\left| x^2+y^2+z^2\leq 4,\;x^2+y^2\geq 1,\;x\geq 0,\;y\geq 0,\;z\geq 0 \right. \right\}\]

• Calcular la integral triple de la función \(f(x,y,z)=z\) sobre la esfera de centro el origen y radio \(a\).

• Resolver la siguiente integral triple usando coordenadas esféricas

\[\int_{-a}^{a}\int_{-\sqrt{a^2-x^2}}^{\sqrt{a^2-x^2}}\int_{0}^{\sqrt{a^2-x^2-y^2}} (x^2+y^2)dV\]

• Calcular la integral triple \(\iiint_R \frac{1}{\sqrt{x^2+y^2+z^2}}dV\) donde \(R\) es la región comprendida entre las esferas de ecuaciones \(x^2+y^2+z^2=4\) y \(x^2+y^2+z^2=9\)