¿Cómo se interpreta una regla difusa?
Imaginemos que tenemos una regla difusa de la foma
Si ![]() entonces
entonces![]() , si no
, si no ![]()
donde ![]() ,
, ![]() y
y ![]() son conjuntos difusos. Por ejemplo, podría ser
son conjuntos difusos. Por ejemplo, podría ser
Si la estación es fría se siente frío, si no, no se siente frío
Supongamos que
| Conjunto | Definición |
|
|
{(p, 0.3), (v, 0.1), (o, 0.4), (i, 0.9)} |
|
|
{(T1, 0.4), (T2, 0.8)} |
|
|
{(T1, 0.6), (T2, 0.2)} |
El valor de verdad de esta regla quedará determinado por un conjunto difuso que interprete el significado de esta regla:
![]()
Teniendo en cuenta la teoría de conjuntos difusos, Zadeh propuso la siguiente interpretación para esta regla:
-
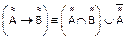 . El grado de pertenencia será:
. El grado de pertenencia será: 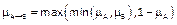
-
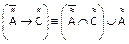 . El grado de pertenencia será:
. El grado de pertenencia será:
![]()
En la práctica hay otras implicaciones que son muy utilizadas por su simplicidad. Una de ellas es la de Mandani, que interpreta la implicación como la relación difusa obtenida por
![]()
De esta manera, la regla puede identificarse por la siguiente relación
![]()
Ejemplo 15. Utilizando la implicación de Mandani, vamos a interpretar la siguiente sentencia:
Si la estación es fría se siente frío, si no, no se siente frío
Esta regla establece una relación entre los universos U={p, v, o, i} y V={T1, T2} que se podrá calcular como:
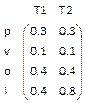 U
U 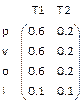 =
=