Ejemplo: Números mucho mayores que 1
Cuestión: ¿Es el número 8 un número mucho mayor que 1? Y, ¿el número 100? ¿Es posible determinar un número a partir del cual los números se consideren mayores que 1 y los números menores no lo sean?
Para definir este conjunto ha de considerar:
- Un conjunto U sobre el cual definir "numeros mayores que 1", podríamos considerar U el conjunto de los números reales.
- Una función, que podemos llamar PERTENECE, que dé el grado de pertenencia de un número real al concepto "número mucho mayor que 1". De esta forma, PERTENECE(x) será el grado en el que el número x es "mucho mayor que 1".
Cuestión: ¿Qué condiciones debería tener PERTENECE(x)?
A la hora de considerar la función PERTENECE, podemos pensar que es lógico imponer que PERTENECE sea una función:
- creciente, es decir, que si x e y son dos números reales cumpliendo que x es menor que y, entonces PERTENECE(x) es menor o igual que PERTENECE(y)
- nula hasta poco después de 1
- que crezca pegada al eje de abscisas y no despeque de él hasta un lugar a convenir a partir del cual el crecimiento sea más rápido hasta llegar a otro lugar, también a convenir, en el que a partir de él valdrá 1.
Podemos pensar en que la función PERTENECE podría tener una gráfica como la siguiente:

Observa que esta función:
- Es creciente.
- Es nula hasta el punto (a,0).
- "Crece pegada" al eje de ascisas y "despega" a partir del punto (a,0) hasta llegar al punto (m,1) en el que después vale 1.
Esta función tiene la siguiente expresión:
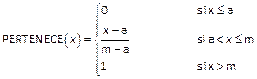
Ejercicio. Vamos a crear con Geogebra esta función.
| Definimos el valor a | a=3 |
| Definimos el valor m | m=3 |
| Definimos la función PERTENECE | PERTENECE(X)=Si[x ≤ a, 0, Si[x ≤ m, (x - a) / (m - a), 1]] |
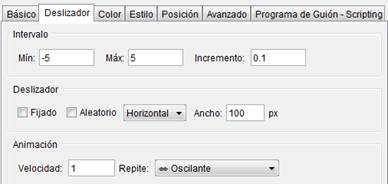
| Definimos las propiedades del deslizador a |
Hacemos clic sobre el objeto a y abrimos su cuadro de propiedades
|
| Definimos las propiedades del deslizador m | 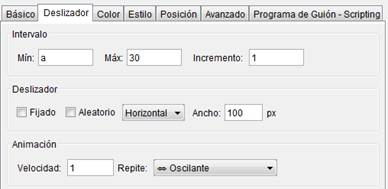 |
Ejemplo 1: ¿Hay otras posibilidades para definir esta función? Abre el fichero perteneceMAY.html para ver otras funciones con las mismas características. ¿Qué diferencias encuentras entre unas y otras funciones?