Ejemplos: Niño, joven, adulto, viejo
Supongamos que el conjunto sobre el que se definen estos conceptos son las edades: 5, 10, 20, 30, 40, 50, 60, 70, 80. Los grados de pertenencia a los conjuntos se definen en la siguiente tabla.
| Elementos (Edad) | Niño | Joven | Adulto | Viejo |
| 5 | 0 | 1 | 0 | 0 |
| 10 | 0 | 1 | 0 | 0 |
| 20 | 0 | 0.8 | 0.8 | 0.1 |
| 30 | 0 | 0.5 | 1 | 0.2 |
| 40 | 0 | 0.2 | 1 | 0.4 |
| 50 | 0 | 0.1 | 1 | 0.6 |
| 60 | 0 | 0 | 1 | 0.8 |
| 70 | 0 | 0 | 1 | 1 |
| 80 | 0 | 0 | 1 | 1 |
Tabla 1: Ejemplos de conjuntos difusos.
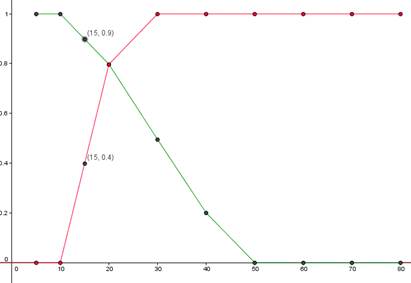
Figura. Representación de los conjuntos Joven y Adulto
Ejercicio. Vamos a crear una función de pertenencia a partir de una tabla de valores cuya gráfica sea la poligonal que une esos puntos.
Para ello seguiremos los siguientes pasos en Geogebra:
| Abrimos la hoja de cálculo | Menú: Vista, Opción: Hoja de Cálculo |
| Tecleamos en las columnas A y B las abscisa y las ordenadas de los puntos | 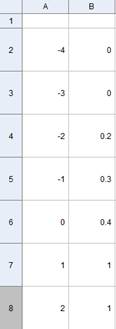 |
| Definimos en la columna C los puntos de la poligonal |
Tecleamos en la celda C2 lo siguiente =(A2,B2) y pulsamos la tecla de salto de línea. Arrastramos esta fórmula estirando del cuadrado señalado hasta la celda C8
|
| En la columna D definimos la función que une los dos primeros puntos |
Escribimos en la celda D2 = Si[A2 ≤ x < A3, y(C2) + (x - x(C2)) (y(C3) - y(C2)) / (x(C3) - x(C2)), 0] |
| Definimos el resto de funciones | Basta arrastrar la fórmula anterior hasta la celda D7 |
| Definimos la función PERTENECE como la suma de las funciones anteriores |
En la ventana de comandos se escribe fun(x) = D2(x) + D3(x) + D4(x) + D5(x) + D6(x)+ D7(x) |
| Definimos un punto px | px=2 y cambiamos sus propiedades para que sea un deslizador |
| Definimos un punto M que se mueva por los puntos de la gráfica | M=(px,fun(px)) |
Una vez realizado este ejercicio, abre el fichero edades.html que se ha construido de esta manera y, considerando una persona de 15 años, contesta a la siguiente pregunta:
¿Con qué grado pertenece a los conjuntos joven y viejo?
