Relaciones entre conjuntos difusos
Vamos ahora a generalizar esta idea para intentar definir una relación difusa entre conjuntos difusos.
A partir de dos conjuntos difusos difusos 
y 
se intentará definir otro que se llamará producto cartesiano y que escribiremos como 
. Este conjunto tiene como función de pertenencia aquella que asigna a cada par ordenado (x,y) el valor mínimo con el x pertenece a 
e y pertenece a 
.
Ejemplo 11: Considerando el ejemplo anterior, tomamos
U=estaciones={primera (p), verano (v), otoño (o), invierno (i)}
V={temperatura superior a 20 grados (T1), temperatura igual o inferior a 20 grados (T2)}
y los conjuntos difusos:
estaciones frías={(p, 0.3), (v, 0.1), (o, 0.4), (i, 0.9)}
sensación de frío ={(T1, 0.4), (T2, 0.8)}
El grado de pertenencia a 
del par (p, T1) es 0.3 ya que p pertenece a 
con grado 0.3, T1 pertenece a 
con grado 0.4 y el mínimo de esos dos valores es 0.2
Cualquier subconjunto del producto cartesiano es un relación entre los conjuntos difusos, una de ellas es el propio producto cartesiano
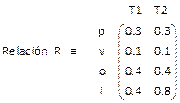
Cuestión.- ¿Qué podría representar la relación anterior?
Consideremos ahora el universo W={bañador (b), traje(t), abrigo(a)} y el conjunto difuso definido sobre él siguiente:
ropa que abriga ={(b, 0.1), (t, 0.5), (a, 0.9)}
El producto cartesiano de 
y 
define una relación entre estos conjuntos
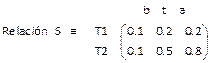
Vamos a calcular ahora la composición de las dos relaciones utilizando la max-min que viene dada por
La idea es que para cada pareja (u, w) se toma como grado de pertenencia a la relación composición el resultado de hacer la siguiente operación:
- Para cada uno de los v en V se toma el mínimo de las funciones de pertencia a las relaciones R y Q de las parejas (u, v) y (v, w) respectivamente.
- El máximo de todos los mínimos anteriores es el valor de la función.
Ejemplo 12: Considerando las relaciónes:
R que relacionaba las estaciones frías con la sensaciones de frío
S que relacionaba las sensación de frío con la ropa de abrigo
vamos a ver cómo se relacionarían las estaciones frías con las ropas de abrigo mediante su composición:
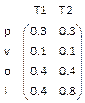
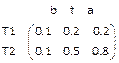
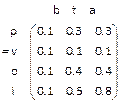
Ejemplo 13. Vamos a practicar esta operación con el fichero composicion.html.
Importante: Estas definiciones, pueden parecer a primera vista arbitrarias y, hasta cierto punto lo son, no obstante en su elección deben tenerse en cuenta los siguientes criterios:
- que sean consistentes con las definiciones paralelas de la teora de conjuntos clásicos, es decir, que ésta pueda considerarse como un caso particular de la teora de conjuntos difusos
- que los modelos basados en la teora reflejen razonablemente bien la realidad y
- que las computaciones que se derivan de la utilización de los modelos sean sencillas y, por tanto, se ejecuten con rapidez.
