Conjuntos difusos con Geogebra

Tabla de Contenidos

1. Introducción
2. Conjuntos difusos: Definiciones y ejemplos
   1. Razonamiento directo con conjuntos no tradicionales
   2. ¿Tiene sentido trabajar con estos conceptos?
   3. ¿Qué es un conjunto difuso?
   4. Ejemplo: Números mucho mayores que 1
   5. Ejemplo: Números próximos a 0
   6. Ejemplo: Número natural grande
   7. Ejemplos: Niño, joven, adulto, viejo
3. Conjuntos difusos: Operaciones
   1. Subconjunto
   2. Igualdad
   3. Complementario
   4. Unión
   5. La intersección
4. Conjuntos difusos: Relaciones difusas
   1. Relaciones difusas entre conjuntos clásicos
   2. Relaciones entre conjuntos difusos
5. Lógica difusa
   1. ¿Casi cierto, muy cierto, algo falso?
   2. ¿Cómo se interpreta una regla difusa?
   3. ¿Cómo se utiliza el Modus Ponens?

Razonamiento directo con conjuntos no tradicionales

Por ejemplo, imaginemos una población de personas con la condición de que los haya de todas las tallas intermedias necesarias para realizar el siguiente argumento. Consideremos una función que indica la talla en cms de la persona x.

Consideremos las siguientes hipótesis:

1. Existe, por lo menos, un hombre pequeño. Llamemos a esa persona PEQ.
2. Para cada persona A se tiene que ..
3. Si A es un hombre pequeño y 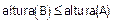entonces B también es pequeño.

Estas tres condiciones parecen perfectamente razonables a partir del acuerdo de que estamos dispuestos a aceptar la existencia de hombres a los que corresponde el adjetivo "pequeño".

Añadamos además la siguiente regla:

4. Si A es pequeño y B verifica 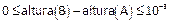entonces B es pequeño.

Esta regla se puede interpretar como que se considerará pequeño a todo aquel que, con una regla de medir alturas muy fina, no se distingue de otro que es pequeño.

En estas condiciones vamos a ver que todos las personas del conjunto son pequeñas. En efecto, tomamos una persona cualquiera de este conjunto que llamaremos PER. Consideramos:

tal que

tal que

.........................................................................

tal que

siendo además .. una persona que cumple que . Nótese que se llegará a un en estas condiciones en pasos.

Aplicando la regla (4) se cumplirá que:

..................................................................................

Por tanto, PER también es pequeño ya que su altura es menor que la de y es pequeño. En la deducción anterior se ha utilizado únicamente el razonamiento directo o "modus ponens".

En principio, se nos hace difcil tener que renunciar, en casos como el mostrado en el ejemplo, de esta regla de deducción tan clásica en Matemática. Por otra parte, el absurdo se produce por aplicación de la condición (4) ya que (1), (2) y (3) únicamente dan significado al concepto pequeño.

Desde el punto de vista de la Lógica Clásica se podra decir entonces que lo válido es la negación de (4), es decir que existen dos personas A y B cumpliendo que A es pequeño y B no lo es verificando además que . Esta afirmación también contradice nuestra intuición.

Conclusión.- Representando todo concepto por un conjunto clásico y efectuando la deducción por los métodos de la lógica tradicional no se obtienen modelos adecuados para la modelización de conceptos imprecisos.