.md .pdf

Contents

Cross product

The second kind of vector product is the so-called cross product or external product that results in a vector. It can be denoted in two alternative (and completely equivalent) ways,

(29) $$\begin{split}\vec{c}=\vec{a}\times\vec{b}\\ \vec{c}=\vec{a}\wedge\vec{b}\end{split}$$

In this course we will normally use the first one.

Definition

The cross product is defined as,

(30) $$\begin{split}\vec{c}=\vec{a}\times\vec{b}=\left\vert \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{array} \right\vert\end{split}$$

that can be express in components using the cofactor expansion of the determinant (minor expansion) in the following way:

(31) $$\vec{c}=\vec{a}\times\vec{b} = (a_yb_z-a_zb_y)\vec{i}+ (a_zb_x-a_xb_z)\vec{j}+ (a_xb_y-a_yb_x)\vec{k}$$

Geometric interpretation

The result of the cross product is a vector that (see Fig. Fig. 14):

• is orthogonal to both initial vectors appearing in the product

• its direction (sense) is given by the right-hand rule

• its modulus is given in function of the modulii of $\vec{a}$ and $\vec{b}$ and the $\sin$ of the angle they form ($\theta$):

(32) $$\vert \vec{a}\times\vec{b}\vert = \vert \vec{a}\vert \vert \vec{b}\vert \sin\theta\vec{c}$$

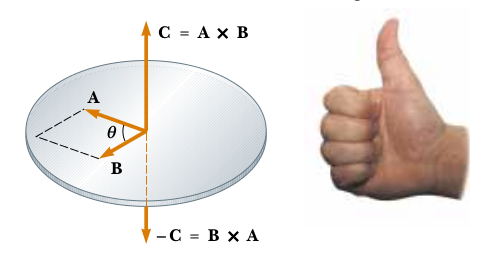
Fig. 14 Illustration of the cross product

Properties

Some properties of the cross product are:

• Distributive: The crossproduct of a vector times a sum of vectors can be expanded in the following way,

(33) $$\vec{a}\times (\vec{b}+\vec{c}) = \vec{a}\times \vec{b}+\vec{a}\times\vec{c}$$

• Product by a scalar: The result of multiplying a scalar times a cross product of vector is the same a multiplying only one of these vectors by the scalar

(34) $$\alpha(\vec{a}\times\vec{b})=(\alpha\vec{a})\times \vec{b}=\vec{a}\times(\alpha\vec{b})$$

• Anticommutative: When the order of the vectors involved in the cross product is changed, the value of the result does not vary but its sign is reversed

(35) $$\vec{a}\times\vec{b}=-\vec{b}\times\vec{a}$$

• Product of a vector by itself: The result of cross multiplying a vector by itself is the null vector

(36) $$\vec{a}\times\vec{a}=\vec{0}$$

Problems and solved examples

• Show that the geometric properties of the cross product are correct

First we will show that the resulting vector of a cross product, $\vec{a}\times\vec{b}$, is perpendicular to both $\vec{a}$ and $\vec{b}$.

Orthogonality between vectors

We know that two vectors are orthogonal if their scalar product is null

(37) $$\begin{split}\vec{a}\cdot(\vec{a}\times\vec{b})=\\(a_x\vec{i}+a_y\vec{j}+a_z\vec{k})\cdot \\ [(a_yb_z-a_zb_y)\vec{i}+(a_zb_x-a_xb_z)\vec{j}+(a_xb_y-a_yb_x)\vec{k}]=0\end{split}$$

This result is unchanged when using $b$ instead of $a$.

My sidebar title

We continue here

(38) $$y=-log(e)$$

And at the end

• This is the text of another problem

Scalar product Mixed product