Contents

Vector derivative

Given a vector there are many possible definitions for its derivative. In physics we are going to assume that the vector depends on a parameter (that, in practice, will be time) and what we want to find is how the vector changes with that parameter.

Definition

(43)\[\vec{f}(t)=f_x(t)\vec{i}+f_y(t)\vec{j}+f_z(t)\vec{k}\]

Its change is,

(43)\[\begin{split} \frac{d\vec{f}}{dt}&=\lim_{\Delta t\rightarrow 0} \frac{\Delta \vec{f}}{\Delta t}\\ &=\lim_{\Delta t\rightarrow 0} \left(\frac{\Delta f_x}{\Delta t}\vec{i}+\frac{\Delta f_y}{\Delta t}\vec{j}+\frac{\Delta f_z}{\Delta t}\vec{k}\right) =\frac{d f_x}{d t}\vec{i}+\frac{d f_y}{d t}\vec{j}+\frac{d f_z}{d t}\vec{k}\end{split}\]

Practical tip

To derive a vector the most simple thing to do is letting usual derivative rules for functions guide you. That is, when we have a vector function expressed as a linear combination of coefficients times a particular vector basis you just need to use the normal derivative rules for addition and product of functions in the following way:

(44)\[\begin{split}\frac{d\vec{f}}{dt}(t)&=\frac{d}{dt}\left(f_x(t)\vec{i}+f_y(t)\vec{j}+f_z(t)\vec{k}\right)\\ &=\frac{d(f_x(t)\vec{i})}{dt}+\frac{d(f_y(t)\vec{j})}{dt}+\frac{d(f_z(t)\vec{k})}{dt} =\vec{i}\frac{df_x}{dt}(t)+\vec{j}\frac{f_y}{dt}(t)+\vec{k}\frac{df_z}{dt}(t)\end{split}\]

Properties

One of the most important properties of the derivative of a vector is that the result is a vector that is always tangential to the curve drawn by the vector when the parameter used in the derivative is changed.

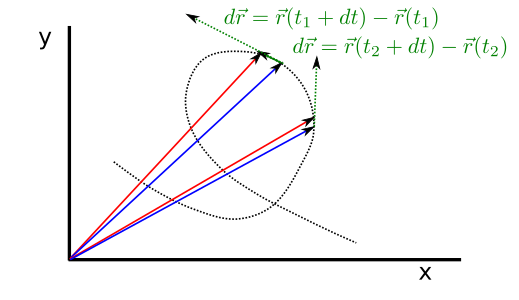
../_images/derivada_tangente.png

Fig. 16 The derivative of a vector is tangent to the curve drawn by the function when the parameter is changed.

For the formal demonstration we will remember that the geometric interpretation of the derivative of a function: the derivative represents the slope of a tangent line to the function in which it is evaluated. Thus, observing the expression of the derivative of a vector in a cartesian basis:

(45)\[\frac{d\vec{f}}{dt}=\sum_i \frac{df_i}{dt}\vec{u}_i\]

we can assert that the derivative \(df_i/dt\) is tangent to the curve created by \(\vec{f}\) in the \(\vec{u}_i\) direction.

Problems and solution examples

Mixed product Integral of a vector