Contents

Scalar product

The first of the vector products is the so-called dot product or internal product that results in an scalar value (in Spanish called producto escalar). This product is denoted by a dot between the two vectors that are being multiplied in the following way:

(18)\[r=\vec{a}\cdot\vec{b}\]

Definition

When the vectors \(\vec{a}\) and \(\vec{b}\) are expressed in the same orthonormal basis the scalar product is the sum of the product of the coordinates of the vectors, coordinate-by-coordinate,

(19)\[\vec{a}\cdot\vec{b}=\sum_i a_i b_i\]

Concept

The scalar product is strongly related with the projection of a vector, \(\vec{A}\), over a second one, \(\vec{B}\), meaning that, if both vectors are placed on a shared origin and we plot the perpendicular line to \(\vec{B}\) that crosses its tip. The projection is the distance from the origin that we measure from the origin along the line that follows the direction of \(\vec{A}\) until it crosses the line perpendicular to \(\vec{B}\) (see Fig. 12).

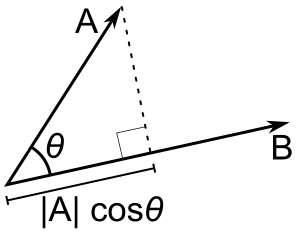
../_images/dot_Product.png

Fig. 12 Projection of a vector over another.

As seen in Fig. Fig. 12 the projection is the modulus of vector \(\vec{A}\) multiplied by the cosine of the angle formed by the vectors. As shown below, the dot product also takes the value,

(20)\[\vec{a}\cdot\vec{b}=\sum_i a_i b_i = \vert\vec{A}\vert\vert\vec{B}\vert\cos\theta\]

That is, the projection of A over B, \(p_{AB}\), is

(21)\[p_{AB}=\frac{\vec{A}\cdot\vec{B}}{\vert\vec{B}\vert}\]

To show the equivalence of both definitions of the dot product above, we must pay attention to the cosine theorem (Fig. Fig. 13). Writing the dot product of the vector \(\vec{c}\) times itself \(\vec{c}\) we find:

(22)\[\vec{c}^2=(\vec{a}-\vec{b})^2 = (a_x-b_x)^2+(a_y-b_y)^2+(a_z-b_z)^2 = \vec{a}^2+\vec{b}^2-2\vec{a}\cdot\vec{b}\]

Comparing this exprssion using the cosine theorem,

(24)\[c^2=a^2+b^2-2ab\cos\gamma\]

we observe

(24)\[\vec{a}\cdot\vec{b}=ab\cos\gamma=a_x b_x+a_y b_y+a_z b_z\]
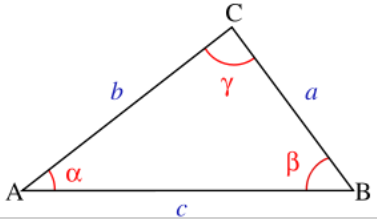
../_images/triangulo.png

Fig. 13 Distances and angles on a triangle

Properties

The scalar product has the following properties,

  • Commutative property: The scalar product does not change when the order of the vectors is altered.

(25)\[\vec{a}\cdot\vec{b}=\vec{b}\cdot \vec{a}\]

  • Associated property: Multiplying an scalar times a scalar vector is equivalent to multiplying a one of the vectors time the scalar.

(26)\[\alpha(\vec{a}\cdot\vec{b})=(\alpha\vec{a})\cdot \vec{b}=\vec{a}\cdot (\alpha \vec{b})\]

  • Distributive property: The scalar product of the sum of two vectors is the sum of the scalar vectors

(27)\[(\vec{a}+\vec{b})\cdot \vec{c}=\vec{a}\cdot\vec{c}+\vec{b}\cdot \vec{c}\]

Problems and solved examples

  • Proof the commutative property of the scalar product

This property follows trivially from the dot product definition,

(28)\[\vec{a}\cdot\vec{b}=\sum_i a_i b_i= \sum_i b_i a_i=\vec{b}\cdot \vec{a}\]
Basic vector operations Cross product