.md .pdf

Contents

Basic vector operations

Vector sum

The simplest operation between vectors is the sum that results in another vector. In the following we will explain this concept in graphical form, we will comment on the mechanical aspects as to how to obtain the resulting sum vector (the algebra of the sum) and the properties of this operation will be discussed.

Concept

As it is shown in Fig. Fig. 7 the result of adding to vectors \(\vec{A}\) and \(\vec{B}\) is a new vector, \(\vec{R}\), obtained after placing the origin of the vector \(\vec{B}\) at the end tip of vector \(\vec{A}\). Vector \(\vec{R}\) is obtained by tracing the line from the origin of \(\vec{A}\) to the tip of \(\vec{B}\).

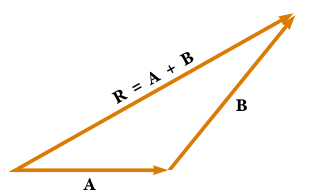
Fig. 7 Vector sum.

Algebra

When we express a vector in a particular basis the coordinates of the resulting vector is the sum of the coordinates of the vectors participating in the sum. If the basis vectors are \(\vec{u}_i\) where the index i runs over the dimensions of space (e.g. i can be \(x\), \(y\) o \(z\) in cartesian or \(\rho\), \(\theta\) o \(\varphi\) in spherical coordinates) and \(a_i\), \(b_i\) y \(r_i\) are, respectively, the coordinates of vectors \(\vec{A}\), \(\vec{B}\) and \(\vec{R}\), then,

(12)\[\vec{R}=\sum_i r_i \vec{u}_i = \vec{A}+\vec{B}=\sum_i a_{i}\vec{u}_i + \sum_i b_{i}\vec{u}_i = \sum_i (a_i+b_i)\vec{u}_i\]

Thus, we have,

(11)\[r_i=a_i+b_i\]

Properties

• Conmutative property: The result of adding \(\vec{A}+\vec{B}\) is the same as the sum \(\vec{B}+\vec{A}\)

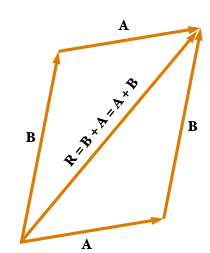
Fig. 8 Conmutative property

This is, again, simple to demonstrate,

(12)\[\vec{A}+\vec{B}=\sum_i a_{i}\vec{u}_i + \sum_i b_{i}\vec{u}_i = \sum_i (a_i+b_i)\vec{u}_i=\sum_i (b_i+a_i)\vec{u}_i=\sum_i b_{i}\vec{u}_i + \sum_i a_{i}\vec{u}_i =\vec{B}+\vec{A}\]

• Associative property: In this case we will show that in sums with multiple terms one can choose the order in which the individual sums are carried out:

(13)\[\vec{A}+(\vec{B}+\vec{C})=(\vec{A}+\vec{B})+\vec{C}\]

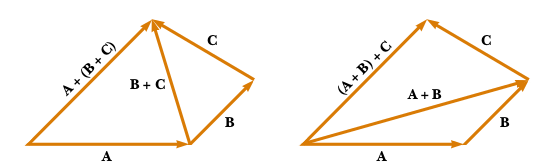
Fig. 9 Proyección de un vector sobre otro

The proof can be carried out, like in previous cases, expressing the vectors using coordinates:

(15)\[\vec{A}+(\vec{B}+\vec{C})=\sum_i a_{i}\vec{u}_i + \left(\sum_i b_{i}\vec{u}_i+\sum_i c_{i}\vec{u}_i\right) = \sum_i \left(a_{i}+b_i+c_i\right)\vec{u}_i = \left(\sum_i a_{i}\vec{u}_i+\sum_i b_{i}\vec{u}_i\right) + \sum_i c_{i}\vec{u}_i =(\vec{A}+\vec{B})+\vec{C}\]

Multiplication by a scalar

Another possible operation is the multiplication by a scalar that results in a re-scaled vector.

Concept

When a vector is multiplied by a scalar (see la Fig. Fig. 10) what we are doing is changing its magnitude (module) without changing the direction. Depending on the sign of the scalar the sense of the vector can be the same the vector had initially (a positive scalar) or the opposite one (a negative scalar).

Fig. 10 Proyección de un vector sobre otro

Algebra

Obtaining the result of multiplying a vector by an scalar is very simple as it follows easily from the usual algebra of scalar, it is just necessary to multiply all the coordinates of the vector by the same scalar:

(15)\[\alpha\vec{A}=\alpha\sum_i a_i\vec{u}_i = \sum_i \alpha a_i \vec{u_i}\]

Vector subtraction

Concept

When a vector, \(\vec{B}\), is subtracted from an initial one, \(\vec{A}\), a new resulting vector, \(\vec{R}\), is obtained where a vector with the direction and modulus of \(\vec{B} but opposite sense has been *added* to \)\vec{A}, as is shown in Fig. Fig. 11

(17)\[\vec{R}=\vec{A}-\vec{B}\]

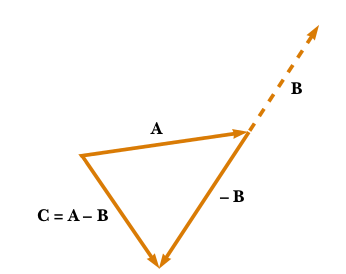
Fig. 11 Proyección de un vector sobre otro

Algebra

Just as with the sum and re-scaling, we can use algebra to check that the coordinates of the resulting vector of a subtraction is the subtraction of the coordinates of the vectors participating in the operation.

(17)\[\vec{A}-\vec{B}=\sum_i a_i \vec{u}_i - \sum_i b_i\vec{u}_i = \sum_i (a_i-b_i) \vec{u}_i\]

Problems and example solutions

Coordinate systems Scalar product