Contents

Mixed product

Definition

Mixed product is a triple vector product that combines the concept of dot and cross products to yield a scalar.

(39)\[P=\vec{a}\cdot(\vec{b}\times\vec{c})\]

Geometric interpretation

The absolute value of the mixed product is the volume of the parallelepiped formed by the 3 vectors (see Fig. Fig. 15).

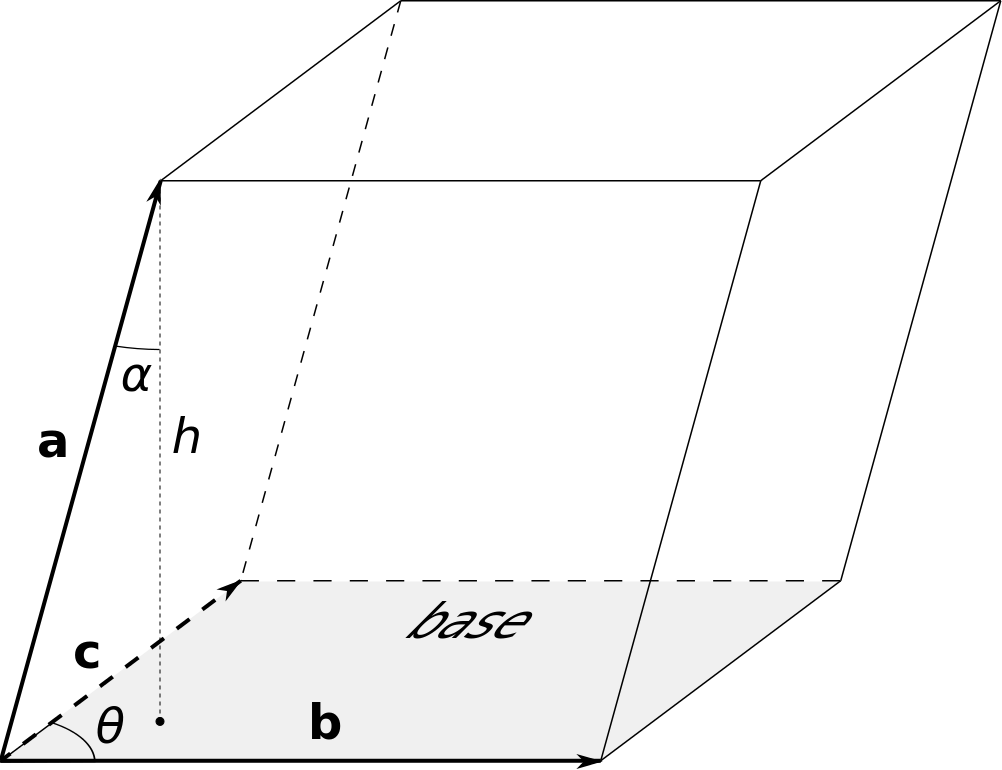
../_images/Parallelepiped_volume.png

Fig. 15 The three vectors involved in the mixed product form a parallelepiped. The absolute value of the mixed product is the volume of the parallelepiped.

To show this property, it is possible to observe that the base of the parallelepiped is given by the cross product between \(\vec{b}\) and \(\vec{c}\), \(b\cdot c \sin\theta\). To calculate the volume it is necessary to multiply the result by the height of the parallelepiped. That can be obtained by the projection of vector \(\vec{a}\) on the vector that is perpendicular on the base, that is \(\vec{b}\times\vec{c}\), and the final is:

(40)\[P=\vec{a}\cdot(\vec{b}\times\vec{c})=a\cdot b\cdot c \sin\theta\cos\alpha\]

Properties

-Cyclic property: The mixed product is invariant under a cyclic permutation of the order of the vectors (\(a\rightarrow b\rightarrow c \Leftrightarrow c\rightarrow a\rightarrow b \Leftrightarrow b\rightarrow c\rightarrow a\)

(41)\[\vec{a}\cdot(\vec{b}\times\vec{c})=\vec{c}\cdot(\vec{a}\times\vec{b})=\vec{b}\cdot(\vec{c}\times\vec{a})\]

In other, non-cyclic permutations, the absolute value of the mixed product is still the same but the sign changes.

Problems and solved examples

Cross product Vector derivative