Contents

Line integral of a vector

Another way to think about the integral of a vector is that, instead of following a parameter, the integrated vector can be projected on the direction of the path followed by the integral. The result of this operation, which is an scalar value, it is called line integral of a vector and is a key concept to understand basic physical concepts like energy.

(47)\[W=\int_{\vec{r}_i}^{\vec{r}_f} \vec{F}\cdot d\vec{r}\]
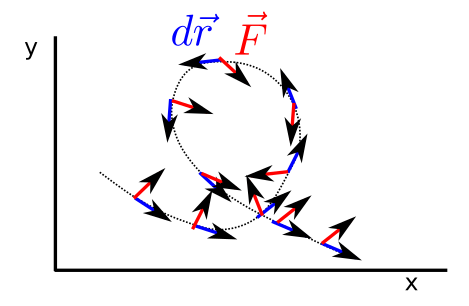
../_images/integral_linea.png

Fig. 17 In a line integral, the integrated vector, calculated on a path, is projected on the tangent vector along that path.

Interpretation

The line integral measures how much the vector \(\vec{F}\) points along the path where the integral is being taken.

Examples

A two-dimensional system is shown in the diagram below:

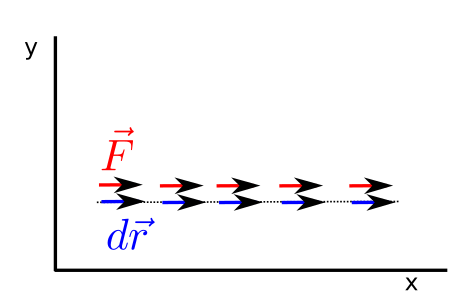
../_images/integral_linea_paralela.png

Fig. 18 Line integral where the integrated vector, \(\vec{F}\), is parallel to the path.

In the figure above it is possible to see how \(\vec{F}\) points along the path in the same sense as the path is being travelled. As a consequence the line integral takes its maximum possible value.

(48)\[W=\int_{\vec{r}_i}^{\vec{r}_f} \vec{F}\cdot d\vec{r}=\int_{\vec{r}_i}^{\vec{r}_f} Fdr=F(r_f-r_i)\]
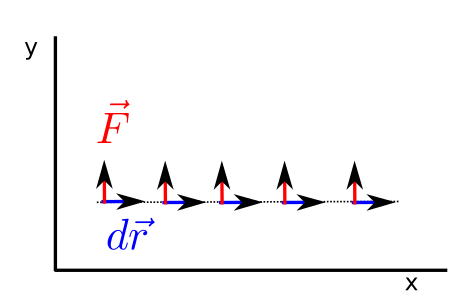
../_images/integral_linea_perp.png

Fig. 19 Line integral where the integrated vector, \(\vec{F}\), is perpendicular to the path.

On the other hand if \(\vec{F}\) is perpendicular to the travelled path, the projection of vector on the path is null and the resulting line integral is null.

(49)\[W=\int_{\vec{r}_i}^{\vec{r}_f} \vec{F}\cdot d\vec{r}=0\]
../_images/integral_linea_perp.png

Fig. 20 Line integral where the integrated vector, \(\vec{F}\), is anti-parallel to the path.

Finally, if the vector \(\vec{R}\) points along the path but in the opposite direction in which it is travelled, the accumulated values are negative and the line integral takes the minimum possible value. This result coincides in absolute value with that of the first example but the sign is just the opposite.

(50)\[W=\int_{\vec{r}_i}^{\vec{r}_f} \vec{F}\cdot d\vec{r}=-\int_{\vec{r}_i}^{\vec{r}_f} Fdr=-F(r_f-r_i)\]
Integral of a vector Fields