Position and trajectory¶
In this chapter we are going to study the movement of an object, analyzing different aspects associated with it. Our point of view is simply going to be descriptive, we are going to discuss how the movement is but we are not going to say why the movement is the way it is (something that we will work out on the next chapter). For example, in Fig. 30 we show the movement of a paper plane doing a loop.
Fig. 30 A paper plane is thrown so that it carries out a loop.¶
Position¶
The first element that we will describe is the position of the object. In order to do so we need to design first who is observing the movement (the observer). Mathematically this is equivalent to defining a reference system in which to place the vectors that are going to describe the different physical magnitudes.
Once the observer has been defined and placed at the origin of the reference system, we will define the position of the object that we are following and to which we will refer with vector \(\vec{r}\).
If the object is quite small we can consider it point-like and its position will be the vector that goes from the origin of the reference system to the exact, well-defined position the object occupies. If, on the other hand, the system is quite large we can design a (small) point inside the object to define position as the vecto that goes from the origin to that small point. For example, when we follow the movement of the plane in Fig. 30 we can place such point, e.g. on the tail of the plane and check how this point moves (ver Fig. 31).
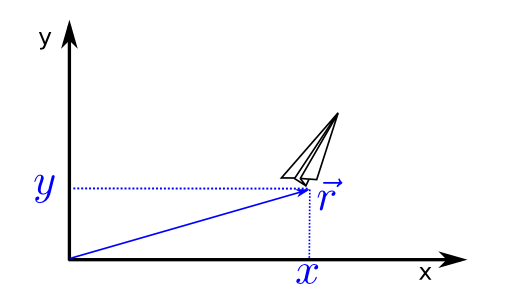
Fig. 31 To follow the plane’s position we place a vector that goes from the origin of the reference system (the observer) to a point of the object (in this case, the tail of the plane).¶
The plane’s position (or the reference point that we are using inside of the plane) changes with time (see Fig. 32). For that reason we say that position is a parametric function of time, \(\vec{r}(t)\).
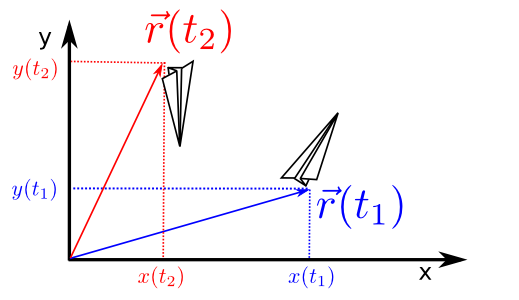
Fig. 32 As time goes by the plane’s position (and its associated vector) changes.¶
Trajectory¶
The main object of study in this chapter is the trjectory that is defined as the set of points \(\{\vec{r}\}\) that are occupied by an object during its movement (see Fig. 33).
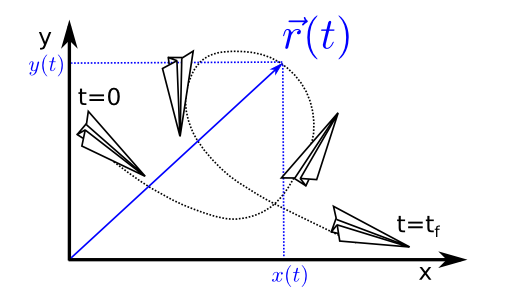
Fig. 33 As time passes, the position vector of the plane changes in a smooth way following the \(\vec{r}(t)\) function. The points it crosses over form a dotted curve that is called trajectory.¶
For example, in Fig. 30 the trajectory is formed by each of the points \(\vec{r}(t)\) through which the planes passes as it carries out a loop. These points follow a curve, presented in Fig. 33, that is the trajectory.