Contents

Examples of movement

Free fall

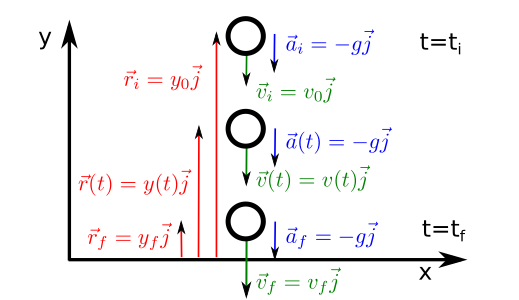
../../_images/caida_libre.png

Fig. 42 Change of position, velocity and acceleration during a free fall movement.

In free fall movement we consider how an object moves when it is thrown, vertically, in the up or down direction with a velocity, \(v_0\) (see Fig. 42). Neglecting the friction of the object with air (drag), the total acceleration of the system is due to gravity. This acceleration of constant module is denoted by the letter g and we are going to consider constant and equal to 9.8\(m/s^2\) (although this is not completely true as its value depends on the latitude). Moreover, we will consider that the direction of this acceleration runs along the y-axis of a cartesian system and that this axis is perpendicular to the floor (see Fig. 42). Thus, we have,

(90)\[\vec{a}=-g \vec{j}\]

In order to find the velocity and the position we simply integrate the acceleration to find,

(91)\[\begin{split}\vec{r}(t)&=\vec{r}_0+\vec{v}_0 t +\frac{1}{2} \vec{a} t^2 = \left(y_0+v_0 t -\frac{1}{2}gt^2\right)\vec{j} ~~(m)\\ \vec{v}(t)&=\frac{d\vec{r}}{dt}=\vec{v}_0 +\vec{a} t = \left(v_0 -gt\right)\vec{j} ~~(m/s)\\ \vec{a}(t)&=\frac{d\vec{v}}{dt}=\vec{a} = -g\vec{j} ~~ (m/s^2)\end{split}\]

Projectile motion

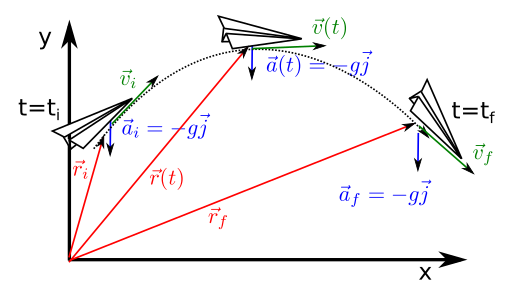
../../_images/tiro_parabolico.png

Fig. 43 Projectile motion is similar to free fall but the object has a non-null horizontal velocity component.

In projectile motion (in Spanish tiro parabólico) is a generalization of the free fall problem where an object is thrown with both vertical and horizontal components of the velocity (see Fig. 43). We are going to assume the following:

  • air-object friction is negligible

  • the curvature of the Earth is small as to consider its surface flat

  • we neglect Earth’s movement

Under these conditions the acceleration of the object (like the paper plane in Fig. 43) is again the gravity, Eq. (90). Thus, we can find velocity and position by direct integration of the acceleration:

(92)\[\begin{split}\vec{r}(t)&=\vec{r}_0+\vec{v}_0 t +\frac{1}{2} \vec{a} t^2 = \left(x_0+v_{0x} t \right)\vec{i}+\left(y_0+v_{0y} t -\frac{1}{2}gt^2\right)\vec{j} ~~(m)\\ \vec{v}(t)&=\frac{d\vec{r}}{dt}=\vec{v}_0 +\vec{a} t = v_{0x}\vec{i}+\left(v_0 -gt\right)\vec{j} ~~(m/s)\\ \vec{a}(t)&=\frac{d\vec{v}}{dt}=\vec{a} = -g\vec{j} ~~(m/s^2)\end{split}\]

Looking at Fig. 43 we can see that this motion has several important points. The first one is the range of the motion, meaning the horizontal distance that the object can travel before touching the ground which we consider at the same height as the initial point. In order to find it we set the height of the movement at the final time equal to zero. This allows us to find the time it takes for the object to touch the ground, \(t_f\):

(93)\[y(t_f)=0\rightarrow y_0+v_{0y} t -\frac{1}{2}gt^2=0 \rightarrow t_f=\frac{-v_{0y}\pm\sqrt{v_{0y}^2+4y_0 g}}{-2g}\]

Using now this time on the horizontal component of the position we can find the range of the projectile,

(94)\[x_f=x(t_f)=x_0+v_{0x}t_f=x_0+v_{0x}t_f \]

Another interesting point is the maximum height of the trajectory (Fig. 43). The object rises if it has positive vertical velocity while it falls if the vertical velocity is negative. This means that, at the maximum height, its vertical velocity is null. We can use this condition to obtain the time it takes to reach maximum height:

(95)\[v_y(t_m)=0\rightarrow v_{0y} -gt_m=0 \rightarrow t_m=v_{0y}/g\]

and, using this time and the vertical position we can obtain the maximum height itself,

(96)\[y(t_m)=y_0+v_{0y}t_m-\frac{1}{2}gt_m^2=y_0+\frac{1}{2} \frac{v_{0y}^2}{g}\]

Problems and solved examples

Acceleration Circular movement