Sistemas de referencia¶

Fig. 87 An observer moving at constant speed is called an inertial observer.¶

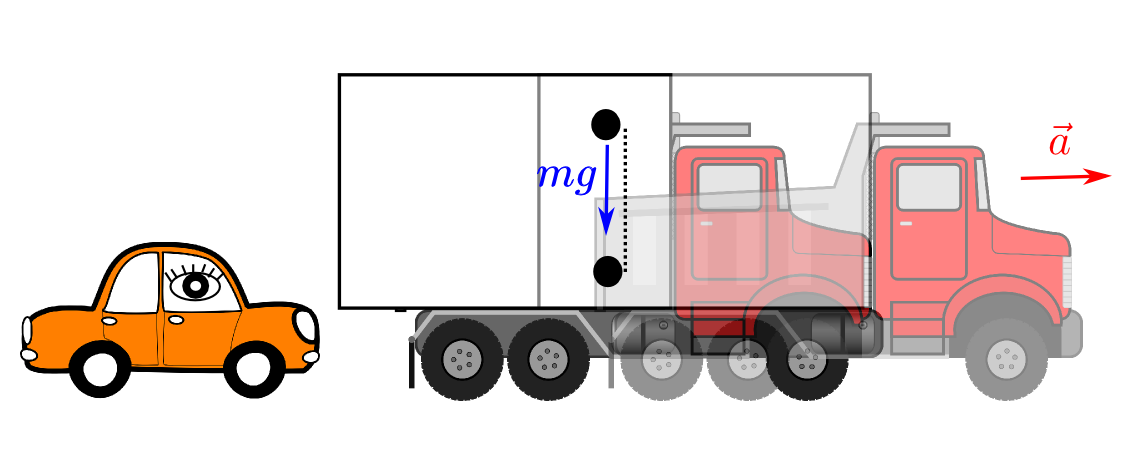
Fig. 88 An inertial observer directly sees the full acceleration of an object.¶

Fig. 89 An accelerated observer is not inertial and does not observe the full acceleration of an object.¶

(172)¶\[\vec{F}_{\text{non-inertial}=\vec{F}_{\text{inertial}}+m\vec{a}_{\text{observer}}\]

(173)¶\[\vec{F}_{\text{central}^\text{observed}=\vec{F}_{\text{inertial}}+m\frac{v^2}{R}\vec{u}_r\]

Fig. 90 An accelerated observer perceives extra forces called inertia forces.¶

Fig. 91 A rotating observer perceives an extra forces called centrifugal force.¶

Magnitudes escalares¶

I am writing an equation inline \(x=-i\hbar\psi=\hat{h}\psi\).

If the equation is by itself,

(174)¶\[-i\hbar\psi=\hat{h}\psi\]

I am going to add a figure

Fig. 92 Here is my figure caption!¶

:::{admonition,warning} This is also Markdown This text is standard Markdown :::

:::{admonition,note} This is also Markdown This text is standard Markdown :::

:::{admonition,tip} This is also Markdown This text is standard Markdown :::

There are many ways to write content in Jupyter Book. This short section covers a few tips for how to do so.

I am going to cite a reference [HdHPK14]

Now I am going to cite section escalares Sec. Magnitudes escalares

The Schrödinger equation is Eq. (195)

I am citing the figure: Fig. 102

I can start solving like this

(175)¶\[x=-2\pi\]

Some text needs to go between sidebars

(176)¶\[y=-log(e)\]

And at the end