Choque: energías¶

Partial conservation of the energy¶

(264)¶\[-\frac{v_{1f}-v_{2f}}{v_{1i}-v_{2i}}=1\]

(265)¶\[-\frac{v_{1f}-v_{2f}}{v_{1i}-v_{2i}}=0\]

(266)¶\[e=-\frac{v_{1f}-v_{2f}}{v_{1i}-v_{2i}}\]

Example: Bouncing ball¶

Fig. 128 A ball that bounces against the floor experiences forces that are vertical, thus that is the only component of the ball’s velocity that changes during the collision.¶

Magnitudes escalares¶

I am writing an equation inline \(x=-i\hbar\psi=\hat{h}\psi\).

If the equation is by itself,

(267)¶\[-i\hbar\psi=\hat{h}\psi\]

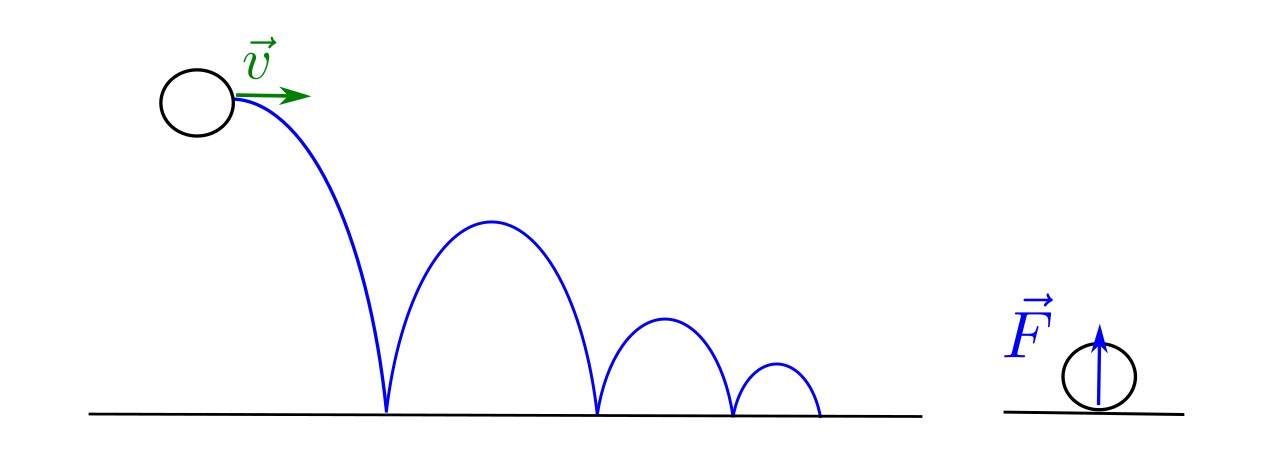
I am going to add a figure

Fig. 129 Here is my figure caption!¶

:::{admonition,warning} This is also Markdown This text is standard Markdown :::

:::{admonition,note} This is also Markdown This text is standard Markdown :::

:::{admonition,tip} This is also Markdown This text is standard Markdown :::

Magnitudes vectoriales¶

There are many ways to write content in Jupyter Book. This short section covers a few tips for how to do so.

I am going to cite a reference [HdHPK14]

Now I am going to cite section escalares Sec. Magnitudes escalares

The Schrödinger equation is Eq. (195)

I am citing the figure: Fig. 102

Unidades¶

Problemas y ejemplos resueltos¶

This is the text of a problem

I can start solving like this

(268)¶\[x=-2\pi\]

Some text needs to go between sidebars

(269)¶\[y=-log(e)\]

And at the end

This is the text of another problem

Física General