Contents

Gradient

Definition

The gradient is an operator (meaning it is an action that we apply over a field) that is defined as,

(63)\[\vec{\nabla}f=\frac{\partial f}{\partial x}\vec{i}+\frac{\partial f}{\partial y}\vec{j}+\frac{\partial f}{\partial z}\vec{k}\]

it is, thus, a vector field associated to a scalara field.

Interpretation

The gradient on a particular set of coordinates points in the direction of maximum variation of the scalar field,

Example

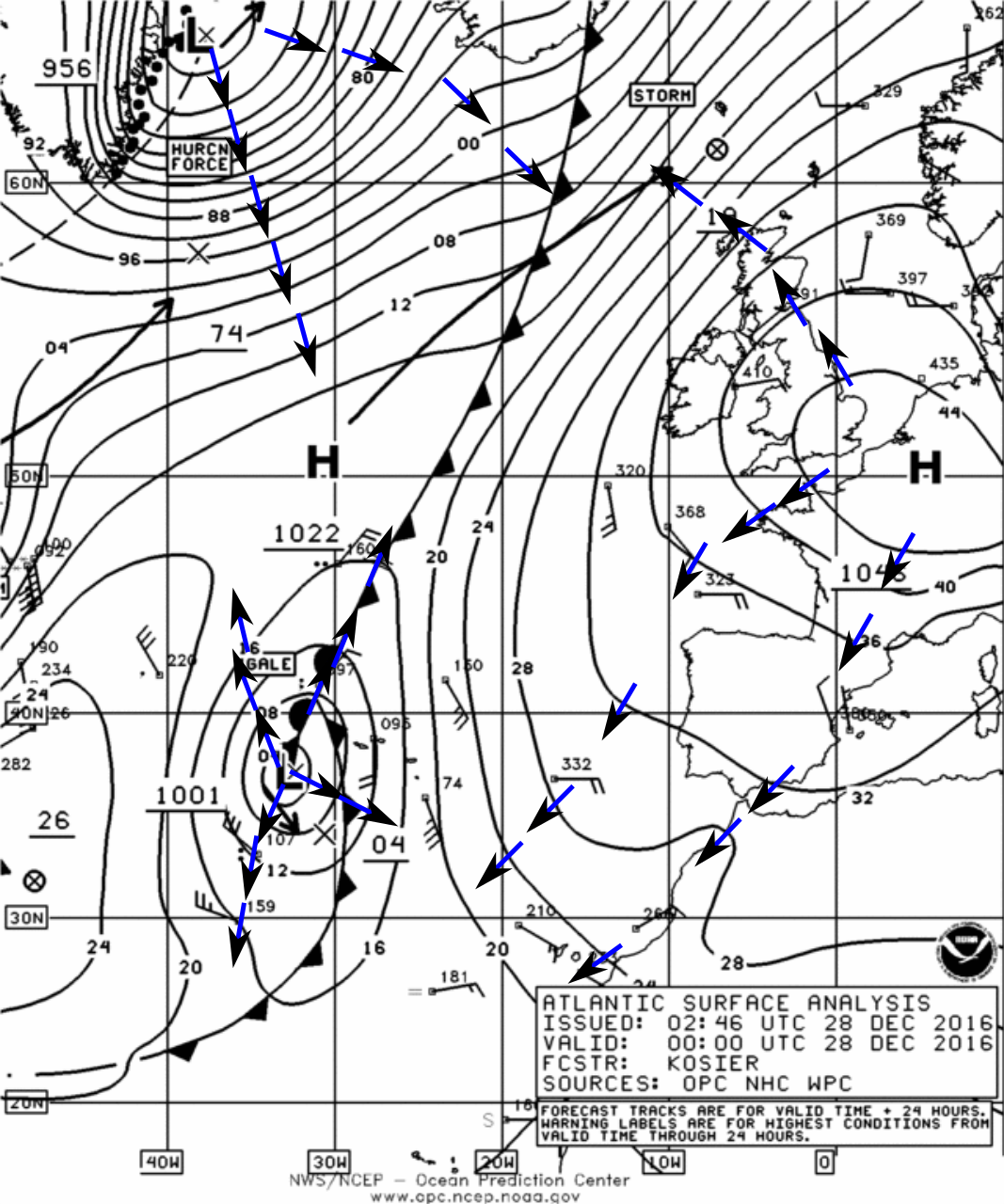
../_images/mapa_gradiente.png

Fig. 26 In the weather map it is possible to plot a vector map with the wind direction at each point.

Introducir imagen del tiempo e indicar el significado de las derivadas parciales

Directional derivative

The directional derivative is a magnitude obtained from the gradient in the following way,

(64)\[D=\vec{\nabla}f \cdot \vec{u}\]

It is thus, the projection of the gradient along a particular direction given by the unitary vector, \(\vec{u}\). This measures the rate of change of the scalar field along the direction of \(\vec{u}\).

Problems and example solutions

Nabla operator Divergence