Contents

Partial derivatives

Introduction

Functions can have a single variable or depend on many of them. The concept of derivative, the variation with respect a one of these variables must be adapted when functions can change along more than one direction.

For example, the velocity of a particle depends on a single variable, time,

(53)\[ \vec{v}=\frac{d\vec{r}}{dt}\]

however, the pressure on a map depends on two variables the longitude, \(\phi\), and its latitude, \(\theta\). Thus, we can think of the way the pressure changes with \(\theta\) and with \(\phi\),

(54)\[ \frac{\partial P}{\partial\theta}, \frac{\partial P}{\partial\phi}\]

Definition

The partial derivative is associated to the infinitesimal variation of a function with respect to one of the multiple variable it depends on. Its rigorous definition comes directly from the usual definition of derivative, keeping all non-changing variables constant. In order to denote the partial derivative we use the symbol \(\partial\) instead of the usual \(d\) that is reserved for the full derivative.

(55)\[\frac{\partial f(x,y,z,...)}{\partial x}=\lim_{\Delta x\rightarrow 0} \frac{f(x+\Delta x,y,z,...)}{\Delta x}\]

Example

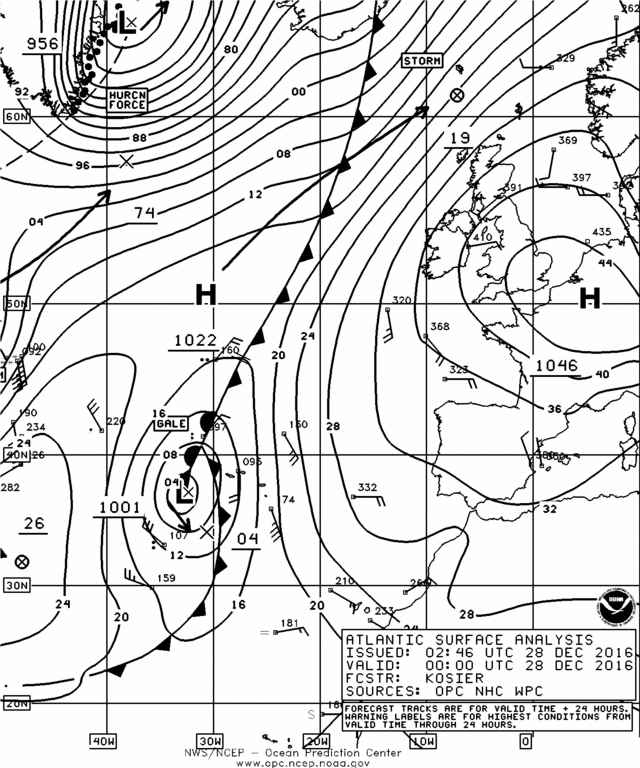
../_images/mapa_tiempo.png

Fig. 25 In a weather map we can observe that properties (pressure, precipitation density, etc.) depend on the position (2 dimensions).

In a weather map we could ask what the variation of the pressure along the north-south or the west-east axis is. These concepts are dealt with using partial derivatives.

Problems and solved examples

  • Find the partial derivatives of the function \(f(x,y,z)=6xy^2z^3+2xy\) with respect to the \(x\), \(y\) y \(z\) variables.

Empezamos trabajando sobre x

Parcial respecto a x

Derivamos la función respecto a x tomando \(y\) y \(z\) como constantes

(56)\[ \frac{\partial f}{\partial x}=6y^2z^3+2y\]

Seguimos trabajando sobre y

Parcial respecto a y

Derivamos la función respecto a x tomando \(y\) y \(z\) como constantes

(57)\[ \frac{\partial f}{\partial y}=12xyz^3+2x\]

Terminamos trabajando sobre z

Parcial respecto a z

Derivamos la función respecto a x tomando \(y\) y \(z\) como constantes

(58)\[ \frac{\partial f}{\partial z}=18xy^2z^2\]
Vector fields Nabla operator