Relación con el triángulo de Pascal
Observación: Una propiedad muy llamativa del triángulo de Sierpinski es su conexión con el triángulo de Pascal. El triángulo de Pascal define de arriba abajo los coeficientes de cada uno de los términos del desarrollo de un binomio elevado a la potencia correspondiente a la profundidad del triángulo.
Ahora, superponiendo un triángulo de Sierpinski sobre el de Pascal (siendo los dos de igual tamaño) se puede comprobar que los triángulos coloreados de azul se corresponden con los números impares y los naranjas con los pares.

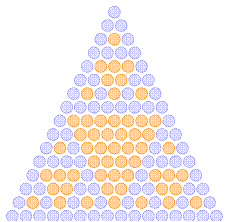
Pregunta: ¿Qué pasaría si se pinta de blanco cuando el número al que corresponde la celda es múltiplo de un número concreto (3, 5, 7) o se pinta de negro cuando no es múltiplo? ¿Qué pasaría si pintamos los números primos del triángulo de Pascal?




El triángulo de Sierpinski se puede generalizar a una figura en 3D,
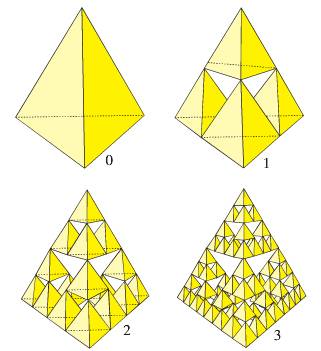
Nota: Así como el triángulo de Sierpinski tiene perímetro infinito y contiene área finita nula, el tetraedro de Sierpinski tiene una superficie infinita que contiene un volumen nulo. Esto se debe a que si el tetraedro inicial tiene arista a.
| Etapa | Volumen total | Superficie total |
| 0 | ||
| n | 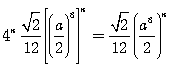 |
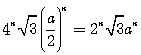 |