16. NumPy

16.1. Overview

NumPy is a first-rate library for numerical programming. NumPy is a popular library in the Python ecosystem and a critical component of the SciPy stack. Numpy allow you to solve problems with less effort and time and with shorter and faster-executing code. This is due to:

• NumPy automatically propagating operations to all values in an array instead of requiring for loops

• A massive collection of functions for working with numerical data

• Many of NumPy’s functions are Python-wrapped C code making them run faster

• Widely used in academia, finance and industry.

• Mature, fast, stable and under continuous development.

In this lecture, we will start a more systematic discussion of both

• NumPy arrays and

• the fundamental array processing operations provided by NumPy.

The NumPy package can be imported by import numpy, but the scientific Python community has developed an unofficial, but strong, convention of importing NumPy using the np alias. It is strongly encouraged for consistency with the rest of the community. Instead of numpy.function(), the function is then called by the shorter np.function(). All of the NumPy code in this and subsequent chapters assumes the following import.

import numpy as np

16.2. NumPy Arrays

The essential problem that NumPy solves is fast array processing.

The most important structure that NumPy defines is an array data type formally called a numpy.ndarray.

NumPy arrays power a large proportion of the scientific Python ecosystem.

To create a NumPy array containing only zeros we use np.zeros

a = np.zeros(3)
a

array([0., 0., 0.])

type(a)

numpy.ndarray

NumPy arrays are somewhat like native Python lists, except that

• Data must be homogeneous (all elements of the same type).

• These types must be one of the data types (dtypes) provided by NumPy.

The most important of these dtypes are:

• float64: 64 bit floating-point number

• int64: 64 bit integer

• bool: 8 bit True or False

There are also dtypes to represent complex numbers, unsigned integers, etc.

On modern machines, the default dtype for arrays is float64

a = np.zeros(3)
type(a[0])

numpy.float64

If we want to use integers we can specify as follows:

a = np.zeros(3, dtype=int)
type(a[0])

numpy.int64

NumPy contains an extensive listing of methods for working with arrays… so much so that it would be impractical to list them all here. However, below are tables of some common and useful methods. It is worth browsing and being aware of them; many are worth committing to memory. If you ever find yourself needing to manipulate an array in some complex fashion, it is worth doing a quick internet search and including “NumPy” in your search. You will likely either find additional NumPy methods that will help or advice on how others solved a similar problem.

Table 1 Common Methods for Generating Arrays

Method	Description
np.array()	Generates an array from another object
np.arange()	Creates an array from [start, stop) with a given step size
np.linspace()	Creates an array from [start, stop] with given number of steps
np.empty()	Creates an “empty” array (actually filled with garbage)
np.zeros()	Generates an array of a given dimensions filled with zeros
np.ones()	Generates an array of a given dimensions filled with ones
np.fromfunction()	Generates an array using a Python function
np.genfromtxt()	Loads text file data into an array
np.loadtxt()	Load text file data into an array (cannot handle missing data)

Table 2 Array Attribute Methods

Method	Description
np.shape(array)	Returns the dimensions of an array
np.ndim(array)	Returns the number of dimensions (e.g., a 2D array is 2)
np.size(array)	Returns the number of elements in an array

Table 3 Array Modification Methods

Method	Description
np.flatten()	Flattens an array in place
np.ravel()	Returns a flattened view of the array without changing the array
np.reshape()	Reshapes an array in place
np.resize()	Returns a resized view of an array without modifying the original
np.transpose()	Returns a view of transposed array
np.vstack()	Vertically stacks an arrays into a new array
np.hstack()	Horizontally stacks an arrays into a new array
np.dstack()	Depth-wise stacks an arrays into a new array
np.vsplit()	Splits an array vertically
np.hsplit()	Splits an array horizontally
np.dsplit()	Splits an array depth-wise
np.meshgrid()	Creates a meshgrid (see chapter 3 for an example)
np.sort()	Sorts elements in array; defaults along last axis
np.argsort()	Returns index values of sorted array
np.fill(x)	Sets all values in an array to x
np.roll()	Rolls the array along the given axis; elements that fall off one end of the array appear at the other
np.floor()	Returns the floor (i.e., rounds down) of all elements in an array
np.round(x, decimals=y)	Rounds every number in an array x to y decimal places by Banker’s rounding

Table 4 Array Measurement and Statistics Methods

Method	Description
np.min()	Returns the minimum value in the array
np.max()	Returns the maximum value in the array
np.argmin()	Returns argument (i.e., index) of min
np.argmax()	Returns argument (i.e., index) of max
np.argrelmax()	Returns argument (i.e., index) of the local max
np.fmin()	Returns the element-by-element min between two arrays of the same size
np.fmax()	Returns the element-by-element max between two arrays of the same size
np.percentile()	Returns the specified percentile
np.mean()	Returns the mean (commonly known as the average)
np.median()	Returns the median
np.std()	Returns the standard deviation; be sure to include ddof=1
np.histogram()	Returns counts and bins for a histogram
np.cumprod()	Returns the cumulative product
np.cumsum()	Returns the cumulative sum
np.sum()	Returns the sum of all elements
np.prod()	Returns the product of all elements
np.ptp()	Returns the peak-to-peak separation of max and min values
np.unique()	Returns an array of unique elements in an array
np.unique_counts()	Returns an array of unique elements in an array and a second array with the frequency of these elements

NumPy has a number of versions of functions (Table 5) that are specifically designed to handle data with missing values.

Table 5 Statistics Methods Dealing with NaNs

Function	Description
np.nanstd()	Standard deveation
np.nanmean()	Mean
np.nanvar()	Variance
np.nanmedian()	Median
np.nanpercentile()	Qth percentile
np.nanquantile()	Qth quantile

The random module in NumPy also includes a large variety of other random number and sequence generators. This includes rng.normal() which generates values centered around zero in a normal distribution. The rng.choice() function selects a random value from a provided array of values, while the rng.shuffle() function randomizes the order of values for a given array. A summary of common NumPy random functions are in Table 6.

Table 6 Summary of Common NumPy np.random Functions

Function	Description
rng.random()	Generates random floats in the range [0,1) in an even distribution
rng.integers()	Generates random integers from a given range in an even distributionb
rng.normal()	Generates random floats in a normal distribution centered around zero
rng.binomial()	Generates random integers in a binomial distribution; takes a probability ,p, and size artuments
rng.poisson()	Generates random floats in a Poisson distribution; takes a target mean argument (lam)
rng.choice()	Selects random values taken from a 1-D array or range
rng.shuffle()	Randomizes the order of an array

16.2.1. Shape and Dimension

Consider the following assignment

z = np.zeros(10)

Here z is a flat array with no dimension — neither row nor column vector.

The dimension is recorded in the shape attribute, which is a tuple

z.shape

(10,)

Here the shape tuple has only one element, which is the length of the array (tuples with one element end with a comma).

To give it dimension, we can change the shape attribute

z.shape = (10, 1)
z

array([[0.],
       [0.],
       [0.],
       [0.],
       [0.],
       [0.],
       [0.],
       [0.],
       [0.],
       [0.]])

z = np.zeros(4)
z.shape = (2, 2)
z

array([[0., 0.],
       [0., 0.]])

In the last case, to make the 2 by 2 array, we could also pass a tuple to the zeros() function, as in z = np.zeros((2, 2)).

16.2.2. Creating Arrays

As we’ve seen, the np.zeros function creates an array of zeros.

You can probably guess what np.ones creates.

Related is np.empty, which creates arrays in memory that can later be populated with data

z = np.empty(3)
z

array([0., 0., 0.])

The numbers you see here are garbage values.

(Python allocates 3 contiguous 64 bit pieces of memory, and the existing contents of those memory slots are interpreted as float64 values)

To set up a grid of evenly spaced numbers use np.linspace

z = np.linspace(2, 4, 5)  # From 2 to 4, with 5 elements

To create an identity matrix use either np.identity or np.eye

z = np.identity(2)
z

array([[1., 0.],
       [0., 1.]])

In addition, NumPy arrays can be created from Python lists, tuples, etc. using np.array

z = np.array([10, 20])                 # ndarray from Python list
z

array([10, 20])

type(z)

numpy.ndarray

z = np.array((10, 20), dtype=float)    # Here 'float' is equivalent to 'np.float64'
z

array([10., 20.])

z = np.array([[1, 2], [3, 4]])         # 2D array from a list of lists
z

array([[1, 2],
       [3, 4]])

See also np.asarray, which performs a similar function, but does not make a distinct copy of data already in a NumPy array.

na = np.linspace(10, 20, 2)
na is np.asarray(na)   # Does not copy NumPy arrays

True

na is np.array(na)     # Does make a new copy --- perhaps unnecessarily

False

To read in the array data from a text file containing numeric data use np.loadtxt or np.genfromtxt—see the documentation for details.

16.2.3. Array Indexing

For a flat array, indexing is the same as Python sequences:

z = np.linspace(1, 2, 5)
z

array([1.  , 1.25, 1.5 , 1.75, 2.  ])

z[0]

np.float64(1.0)

z[0:2]  # Two elements, starting at element 0

array([1.  , 1.25])

z[-1]

np.float64(2.0)

For 2D arrays the index syntax is as follows:

z = np.array([[1, 2], [3, 4]])
z

array([[1, 2],
       [3, 4]])

z[0, 0]

np.int64(1)

z[0, 1]

np.int64(2)

And so on.

Note that indices are still zero-based, to maintain compatibility with Python sequences.

Columns and rows can be extracted as follows

z[0, :]

array([1, 2])

z[:, 1]

array([2, 4])

NumPy arrays of integers can also be used to extract elements

z = np.linspace(2, 4, 5)
z

array([2. , 2.5, 3. , 3.5, 4. ])

indices = np.array((0, 2, 3))
z[indices]

array([2. , 3. , 3.5])

Finally, an array of dtype bool can be used to extract elements

z

array([2. , 2.5, 3. , 3.5, 4. ])

d = np.array([0, 1, 1, 0, 0], dtype=bool)
d

array([False,  True,  True, False, False])

z[d]

array([2.5, 3. ])

We’ll see why this is useful below.

An aside: all elements of an array can be set equal to one number using slice notation

z = np.empty(3)
z

array([2. , 3. , 3.5])

z[:] = 42
z

array([42., 42., 42.])

16.2.4. Array Methods

Arrays have useful methods, all of which are carefully optimized

a = np.array((4, 3, 2, 1))
a

array([4, 3, 2, 1])

a.sort()              # Sorts a in place
a

array([1, 2, 3, 4])

a.sum()               # Sum

np.int64(10)

a.mean()              # Mean

np.float64(2.5)

a.max()               # Max

np.int64(4)

a.argmax()            # Returns the index of the maximal element

np.int64(3)

a.cumsum()            # Cumulative sum of the elements of a

array([ 1,  3,  6, 10])

a.cumprod()           # Cumulative product of the elements of a

array([ 1,  2,  6, 24])

a.var()               # Variance

np.float64(1.25)

a.std()               # Standard deviation

np.float64(1.118033988749895)

a.shape = (2, 2)
a.T                   # Equivalent to a.transpose()

array([[1, 3],
       [2, 4]])

Another method worth knowing is searchsorted().

If z is a nondecreasing array, then z.searchsorted(a) returns the index of the first element of z that is >= a

z = np.linspace(2, 4, 5)
z

array([2. , 2.5, 3. , 3.5, 4. ])

z.searchsorted(2.2)

np.int64(1)

Many of the methods discussed above have equivalent functions in the NumPy namespace

a = np.array((4, 3, 2, 1))

np.sum(a)

np.int64(10)

np.mean(a)

np.float64(2.5)

16.3. Operations on Arrays

16.3.1. Arithmetic Operations

The operators +, -, *, / and ** all act elementwise on arrays

a = np.array([1, 2, 3, 4])
b = np.array([5, 6, 7, 8])
a + b

array([ 6,  8, 10, 12])

a * b

array([ 5, 12, 21, 32])

We can add a scalar to each element as follows

a + 10

array([11, 12, 13, 14])

Scalar multiplication is similar

a * 10

array([10, 20, 30, 40])

The two-dimensional arrays follow the same general rules

A = np.ones((2, 2))
B = np.ones((2, 2))
A + B

array([[2., 2.],
       [2., 2.]])

A + 10

array([[11., 11.],
       [11., 11.]])

A * B

array([[1., 1.],
       [1., 1.]])

In particular, A * B is not the matrix product, it is an element-wise product.

16.3.2. Matrix Multiplication

With Anaconda’s scientific Python package based around Python 3.5 and above, one can use the @ symbol for matrix multiplication, as follows:

A = np.ones((2, 2))
B = np.ones((2, 2))
A @ B

array([[2., 2.],
       [2., 2.]])

We can also use @ to take the inner product of two flat arrays

A = np.array((1, 2))
B = np.array((10, 20))
A @ B

np.int64(50)

In fact, we can use @ when one element is a Python list or tuple

A = np.array(((1, 2), (3, 4)))
A

array([[1, 2],
       [3, 4]])

A @ (0, 1)

array([2, 4])

Since we are post-multiplying, the tuple is treated as a column vector.

16.3.3. Mutability and Copying Arrays

NumPy arrays are mutable data types, like Python lists.

In other words, their contents can be altered (mutated) in memory after initialization.

We already saw examples above.

Here’s another example:

a = np.array([42, 44])
a

array([42, 44])

a[-1] = 0  # Change last element to 0
a

array([42,  0])

Mutability leads to the following behavior

a = np.random.randn(3)
a

array([-0.01534458, -0.5085729 ,  0.02311208])

b = a
b[0] = 0.0
a

array([ 0.        , -0.5085729 ,  0.02311208])

What’s happened is that we have changed a by changing b.

The name b is bound to a and becomes just another reference to the array.

Hence, it has equal rights to make changes to that array.

This is in fact the most sensible default behavior!

It means that we pass around only pointers to data, rather than making copies.

Making copies is expensive in terms of both speed and memory.

16.3.3.1. Making Copies

It is of course possible to make b an independent copy of a when required.

This can be done using np.copy

a = np.random.randn(3)
a

array([0.01527255, 1.1412519 , 0.39482665])

b = np.copy(a)
b

array([0.01527255, 1.1412519 , 0.39482665])

Now b is an independent copy (called a deep copy)

b[:] = 1
b

array([1., 1., 1.])

a

array([0.01527255, 1.1412519 , 0.39482665])

Note that the change to b has not affected a.

16.4. Additional Functionality

Let’s look at some other useful things we can do with NumPy.

16.4.1. Vectorized Functions

NumPy provides versions of the standard functions log, exp, sin, etc. that act element-wise on arrays

z = np.array([1, 2, 3])
np.sin(z)

array([0.84147098, 0.90929743, 0.14112001])

This eliminates the need for explicit element-by-element loops such as

n = len(z)
y = np.empty(n)
for i in range(n):
    y[i] = np.sin(z[i])

Because they act element-wise on arrays, these functions are called vectorized functions.

In NumPy-speak, they are also called ufuncs, which stands for “universal functions”.

As we saw above, the usual arithmetic operations (+, *, etc.) also work element-wise, and combining these with the ufuncs gives a very large set of fast element-wise functions.

z

array([1, 2, 3])

(1 / np.sqrt(2 * np.pi)) * np.exp(- 0.5 * z**2)

array([0.24197072, 0.05399097, 0.00443185])

Not all user-defined functions will act element-wise.

For example, passing the function f defined below a NumPy array causes a ValueError

def f(x):
    return 1 if x > 0 else 0

The NumPy function np.where provides a vectorized alternative:

x = np.random.randn(4)
x

array([ 0.68931175, -0.20297224, -0.92924391,  0.42257762])

np.where(x > 0, 1, 0)  # Insert 1 if x > 0 true, otherwise 0

array([1, 0, 0, 1])

You can also use np.vectorize to vectorize a given function

f = np.vectorize(f)
f(x)                # Passing the same vector x as in the previous example

array([1, 0, 0, 1])

However, this approach doesn’t always obtain the same speed as a more carefully crafted vectorized function.

16.4.2. Comparisons

As a rule, comparisons on arrays are done element-wise

z = np.array([2, 3])
y = np.array([2, 3])
z == y

array([ True,  True])

y[0] = 5
z == y

array([False,  True])

z != y

array([ True, False])

The situation is similar for >, <, >= and <=.

We can also do comparisons against scalars

z = np.linspace(0, 10, 5)
z

array([ 0. ,  2.5,  5. ,  7.5, 10. ])

z > 3

array([False, False,  True,  True,  True])

This is particularly useful for conditional extraction

b = z > 3
b

array([False, False,  True,  True,  True])

z[b]

array([ 5. ,  7.5, 10. ])

Of course we can—and frequently do—perform this in one step

z[z > 3]

array([ 5. ,  7.5, 10. ])

16.4.3. Sub-packages

NumPy provides some additional functionality related to scientific programming through its sub-packages.

We’ve already seen how we can generate random variables using np.random

z = np.random.randn(10000)  # Generate standard normals
y = np.random.binomial(10, 0.5, size=1000)    # 1,000 draws from Bin(10, 0.5)
y.mean()

np.float64(5.033)

Another commonly used subpackage is np.linalg

A = np.array([[1, 2], [3, 4]])

np.linalg.det(A)           # Compute the determinant

np.float64(-2.0000000000000004)

np.linalg.inv(A)           # Compute the inverse

array([[-2. ,  1. ],
       [ 1.5, -0.5]])

Much of this functionality is also available in SciPy, a collection of modules that are built on top of NumPy.

For a comprehensive list of what’s available in NumPy see this documentation.

16.4.3.1. Missing Data

Real data sets frequently contain gaps or missing values, so it is important to be able to deal with missing data. When importing data into NumPy, there are two commonly employed functions, np.genfromtxt() and np.loadtxt(). Though these are largly analogous functions in terms of capabilities, there is a key difference in that np.genfromtxt() can handle missing data while np.loadtxt() cannot. This means if your data set may contain gaps, you should use np.genfromtxt().

In the event the data file contains a gap, the np.genfromtxt() function will place a nan in that loacation by default. The nan stands for “not a number” and is simply a placeholder.

Some data files use placeholder values instead of no value at all. These placeholders are often -1, 0, 999, or some physically meaningless or improbable value. If you have an alternative values you want in the missing data location, you can specify this using the filling_values= argument. As an example below, the missing value is replaced with a 999.

16.4.4. Random Number Generation

Stochastic simulations are a common tool in the sciences and rely on a series of random numbers, so it is worth addressing their generation using NumPy. Depending upon the requirements of the simulation, random numbers may be a series of floats or integers, and they may be generated from various ranges of values. The numbers may also be generated as a uniform distribution where all values are equally likely or biased a distribution where some values are more probable than others. Below are random number functions from the NumPy random module useful in generating random number distributions to suit the needs of your simulations.

Note

Software generated random numbers are really pseudorandom numbers. However, they are close enough to random for most engineering simulations and will be referred to as “random numbers” herein.

16.4.4.1. Uniform Distribution

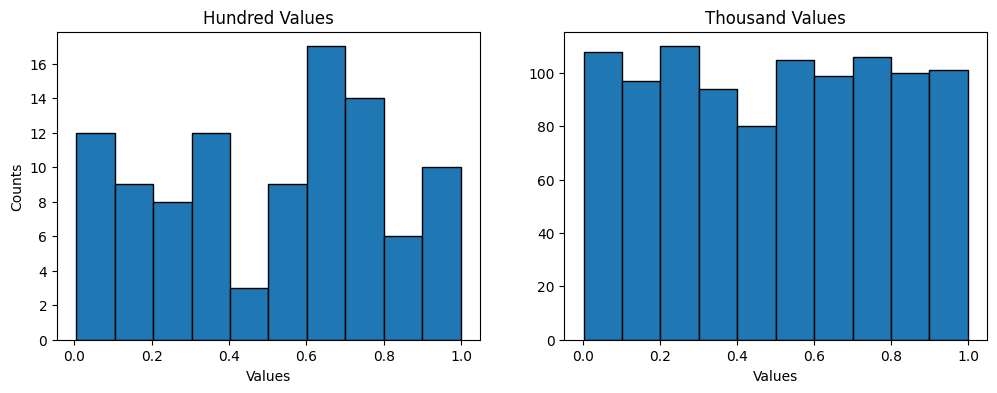
The simplest distribution is the uniform distribution of random numbers where every number in the range has an equal probability of occurring. The distribution may not always appear as even with small sample sizes due to the random nature of the number generation, but as a larger population of samples is generated, the relative distribution will appear more even. The histograms below are of a hundred (left) and a hundred thousand (right) randomly generated floats from the [0,1) range in an even distribution. While the plot on the right appears more even, this is mostly an effect of the different scales.

import numpy as np
import matplotlib.pyplot as plt
# The following line is not necessary if it is used in a script
%matplotlib inline

rng = np.random.default_rng(seed=18)
fig = plt.figure(figsize=(12,4))
ax1 = fig.add_subplot(1,2,1)
ax1.hist(rng.random(100), edgecolor='k')
ax1.set_ylabel('Counts')
ax1.set_xlabel('Values')
ax1.set_title('Hundred Values')
ax2 = fig.add_subplot(1,2,2)
ax2.hist(rng.random(1000), edgecolor='k')
ax2.set_xlabel('Values')
ax2.set_title('Thousand Values')
plt.show()

16.4.4.2. Binomial Distribution

A binomial distribution results when values are generated from two possible outcomes. The two outcomes are represented by a 0 or 1 with the probability, p, of a 1 being generated. Binomial distributions are generated by the NumPy random module using the rng.binomial() function call.

rng = np.random.default_rng()

rng.binomial(t, p, size=n)

The t argument is the number of trials while the size= argument is the number of generated values. For example, if t = 2, two binomial values are generated and the sum is returned, which may be 0, 1, or 2. Basic probability predicts that these sums will occur in a 1:2:1 ratio, respectively. If t is increased to 10, a shape more closely representing a bell curve is obtained. 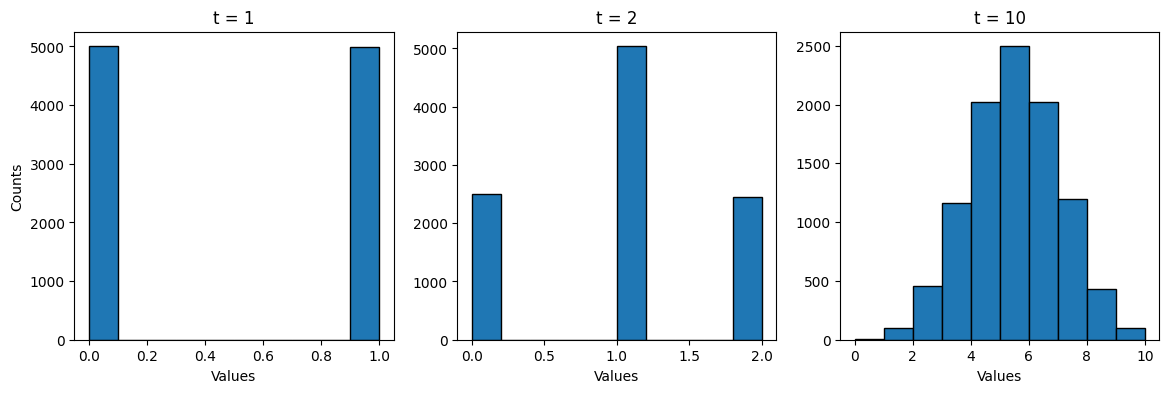A Bernoulli distribution is the specific instance of a binomial distribution where t = 1. The histograms below are of a hundred randomly generated numbers in a binomial distribution with p = 0.5 and where t = 1 (left), t = 2 (center), and t = 10 (right).

import numpy as np
import matplotlib.pyplot as plt
# The following line is not necessary if it is used in a script
%matplotlib inline

fig = plt.figure(figsize=(14,4))

ax1 = fig.add_subplot(1,3,1)
ax1.hist(rng.binomial(1, p=0.5, size=10000), edgecolor='k')
ax1.set_ylabel('Counts')
ax1.set_xlabel('Values')
ax1.set_title('t = 1')
ax2 = fig.add_subplot(1,3,2)
ax2.hist(rng.binomial(2, p=0.5, size=10000), edgecolor='k')
ax2.set_xlabel('Values')
ax2.set_title('t = 2')
ax3 = fig.add_subplot(1,3,3)
ax3.hist(rng.binomial(10, p=0.5, size=10000), edgecolor='k')
ax3.set_xlabel('Values')
ax3.set_title('t = 10')
plt.show()

16.4.4.3. Poisson Distribution

A Poisson distribution is a probability distribution of how likely it is for independent events to occur in a given interval (time or space) with a known average frequency (\(\lambda\)). Each sample in a poisson distribution is a count of how many events have occurred in the time interval, so they are always integers. NumPy can generate integers in a Poisson distribution using the rng.poisson() function, which accepts two arguments.

rng.poisson(lam=1.0, size=n)

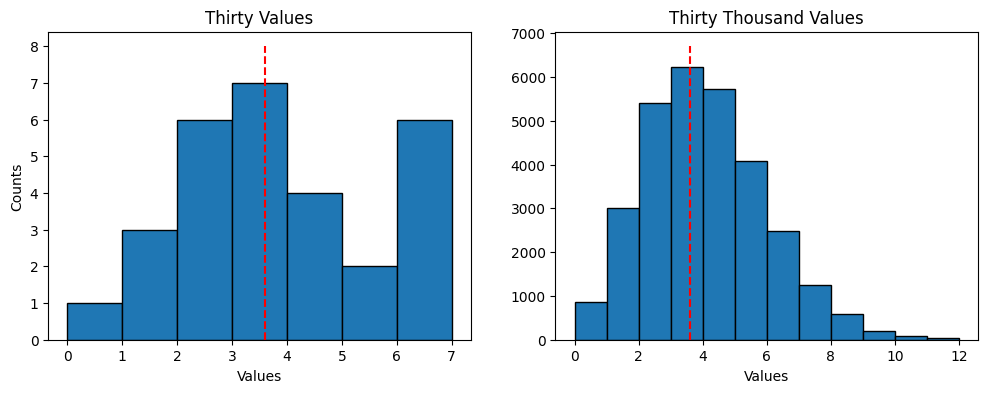
The first argument, \(\lambda\) (lam), is the statistical mean for the values generated, and the second argument, size, is the requested number of values. For example, a Geiger counter can be simulated detecting background radiation in a location that is known to have an average of 3.6 radiation counts per second with the following function call.

rng = np.random.default_rng(seed=20)
rng.poisson(lam=3.6, size=30)

A histogram of the simulation values is shown below with diferent samples. In addition, the larger number of values results in a classic Poisson distribution curve which appears something like a bell curve with more tapering on the high end.

import numpy as np
import matplotlib.pyplot as plt
# The following line is not necessary if it is used in a script
%matplotlib inline

fig = plt.figure(figsize=(12,4))
ax1 = fig.add_subplot(1,2,1)
ax1.hist(rng.poisson(lam=3.6, size=30), bins=range(0,8), edgecolor='k')
ax1.vlines(3.6, 0, 8, 'r', linestyle='dashed')
ax1.set_ylabel('Counts')
ax1.set_xlabel('Values')
ax1.set_title('Thirty Values')
ax2 = fig.add_subplot(1,2,2)
ax2.hist(rng.poisson(lam=3.6, size=30000), bins=range(0,13), edgecolor='k')
ax2.vlines(3.6, 0, 6700, 'r', linestyle='dashed')
ax2.set_xlabel('Values')
ax2.set_title('Thirty Thousand Values')
plt.show()

16.4.4.4. Other Functions

The random module in NumPy also includes a large variety of other random number and sequence generators. This includes rng.normal() which generates values centered around zero in a normal distribution. The rng.choice() function selects a random value from a provided array of values, while the rng.shuffle() function randomizes the order of values for a given array. Other random distribution functions can be found on the NumPy website (see NumPy documentation). A summary of common NumPy random functions are in the following Table.

Summary of Common NumPy np.random Functions

Function	Description
rng.random()	Generates random floats in the range [0,1) in an even distribution
rng.integers()	Generates random integers from a given range in an even distributionb
rng.normal()	Generates random floats in a normal distribution centered around zero
rng.binomial()	Generates random integers in a binomial distribution; takes a probability ,p, and size artuments
rng.poisson()	Generates random floats in a Poisson distribution; takes a target mean argument (lam)
rng.choice()	Selects random values taken from a 1-D array or range
rng.shuffle()	Randomizes the order of an array

16.4.5. Example

Consider the polynomial expression

(16.1)\[p(x) = a_0 + a_1 x + a_2 x^2 + \cdots a_N x^N = \sum_{n=0}^N a_n x^n\]

Write a function that uses NumPy arrays and array operations for its computations.

(Such functionality is already implemented as np.poly1d, but for the sake of the exercise don’t use this class)

• Hint: Use np.cumprod()

Solution

def p(x, coef):
    X = np.ones_like(coef)
    X[1:] = x
    y = np.cumprod(X)   # y = [1, x, x**2,...]
    return coef @ y

# Let\'s test it
x = 2
coef = np.linspace(2, 4, 3)
print(coef)
print(p(x, coef))
# For comparison
q = np.poly1d(np.flip(coef))
print(q(x))

[2. 3. 4.]
24.0
24.0

16.5. Further Reading

The NumPy documentation is well written and a good resource. Any Python book on scientific computing will discuss or use NumPy at some level.

1. NumPy Website. http://www.numpy.org/ (free resource)

2. NumPy User Guide. https://numpy.org/doc/stable/user/index.html#user (free resource)

3. The official NumPy documentation (free resource)

4. VanderPlas, J. Python data Science Handbook: Essential Tools for Working with Data, 1st ed.; O’Reilly: Sebastopol, CA, 2017, chapter 2. Freely available from the author at https://jakevdp.github.io/PythonDataScienceHandbook/ (free resource)

5. Scientific Python Lectures (free resource)