Monthly Mean Sea Level
Contents
3. Monthly Mean Sea Level#
Simulate Monthly Mean Sea Level (MMSL) using a multivariate-linear regression model based on the annual SST PCs
inputs required:
WaterLevel historical data from a tide gauge at the study site
Historical and simulated Annual PCs
in this notebook:
Obtain monthly mean sea level anomalies (MMSLA) from the tidal gauge record
Perform linear regression between MMSLA and annual PCs
Obtain predicted timeseries of MMSLA based on simulated timeseries of annual PCs
Workflow:
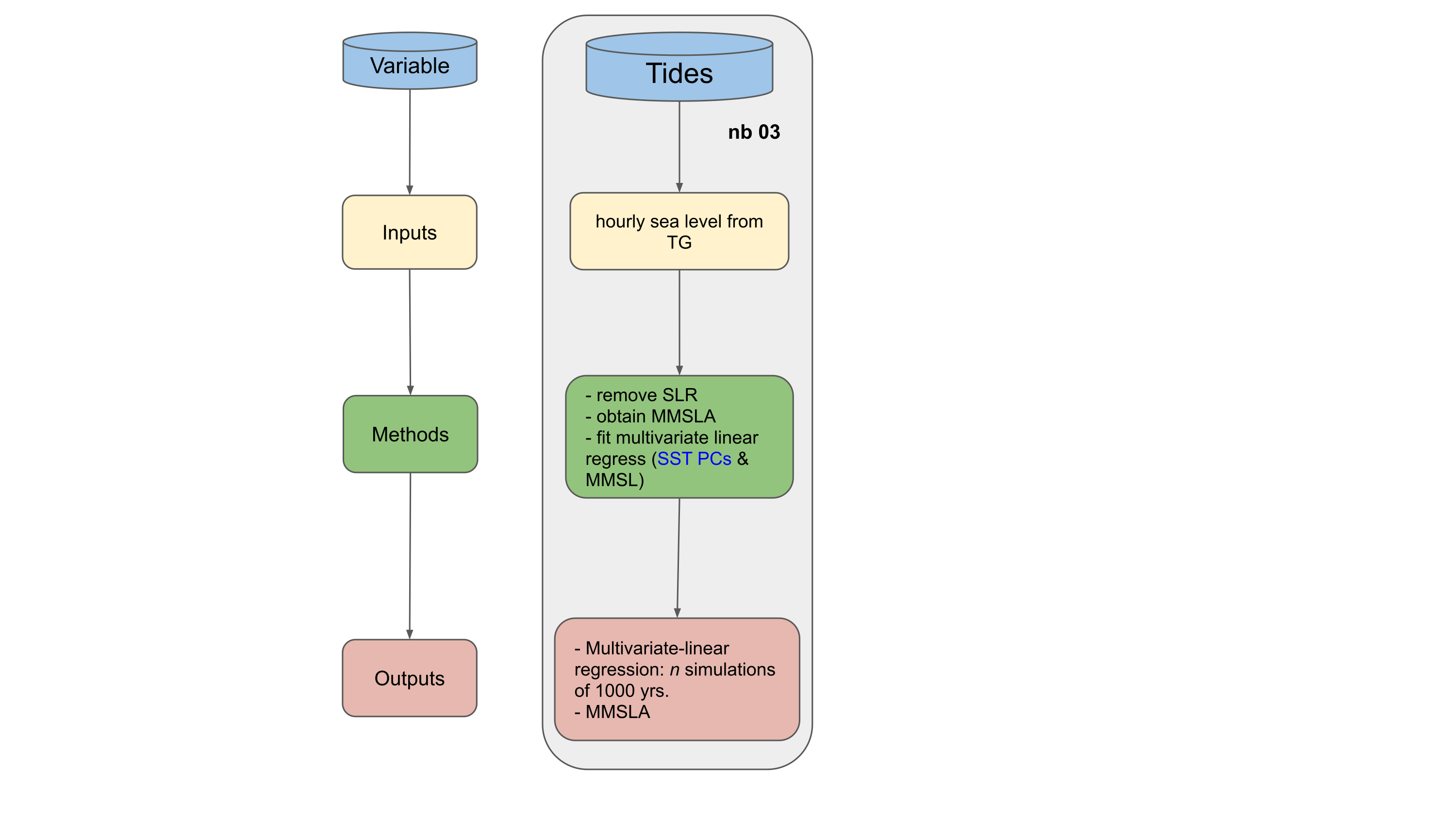
Monthly sea level variability is typically due to processes occurring at longer timescales than the daily weather. Slowly varying seasonality and anomalies due to ENSO are retained in the climate emulator via the principle components (APC) used to develop the AWT. A multivariate regression model containing a mean plus annual and seasonal cycles at 12-month and 6-month periods for each APC covariate was fit to the MMSLA. This simple model explains ~75% of the variance without any specific information regarding local conditions (i.e., local anomalies due to coastal shelf dynamics, or local SSTAs) and slightly underpredicts extreme monthly sea level anomalies by ~10 cm. While this component of the approach is a subject of ongoing research, the regression model produces an additional ~0.35 m of regional SWL variability about mean sea level, which was deemed sufficient for the purposes of demonstrating the development of the stochastic climate emulator.
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# basic import
import os
import os.path as op
# python libs
import numpy as np
import pandas as pd
from numpy.random import multivariate_normal
import xarray as xr
from scipy.stats import linregress
from scipy.optimize import curve_fit
# DEV: override installed teslakit
import sys
sys.path.insert(0, op.join(os.path.abspath(''), '..','..', '..', '..'))
# teslakit
from bluemath.teslakit2.toolkit.averages import running_mean, monthly_mean
from bluemath.teslakit2.util.time_operations import date2yearfrac as d2yf
from bluemath.teslakit2.io.aux import save_nc
from bluemath.teslakit2.plotting.tides import Plot_Tide_SLR, Plot_Tide_RUNM, Plot_Tide_MMSL, \
Plot_Validate_MMSL_tseries, Plot_Validate_MMSL_scatter, Plot_MMSL_Prediction, \
Plot_MMSL_Histogram
Warning: ecCodes 2.21.0 or higher is recommended. You are running version 2.20.0
3.1. Files and paths#
# project path
p_data = r'/media/administrador/HD2/SamoaTonga/data'
site = 'Samoa'
p_site = op.join(p_data, site)
# deliverable folder
p_deliv = op.join(p_site, 'd09_TESLA')
# output path
p_out = op.join(p_deliv,'TIDE')
if not os.path.isdir(p_out): os.makedirs(p_out)
# input data
TG_file = op.join(p_out,'tide_astro_hist_h056a.nc')
sst_awt_file = op.join(p_deliv,'SST','SST_KMA.nc') # KMA results
pcs_sim_m_file = op.join(p_deliv,'SST','SST_PCs_sim_m.nc') # PCs resampled to monthly
# output data
mmsl_hist_file = op.join(p_out,'tide_mmsl_hist.nc') # historical mmsl from TG
mmsl_sim_file = op.join(p_out,'tide_mmsl_sim.nc') # simulated mmsl from PCs
model_coefs_file = op.join(p_out,'mmsl_model_params.nc') # fitting parameters of the regression model
3.2. Parameters#
# --------------------------------------
# load data and set parameters
WL_split = xr.open_dataset(TG_file) # water level historical data (tide gauge)uge)
WL = WL_split.WaterLevels
SST_KMA = xr.open_dataset(sst_awt_file) # SST Anual Weather Types PCs
SST_PCs_sim_m = xr.open_dataset(pcs_sim_m_file, decode_times=True) # simulated SST PCs (monthly)
# parameters for mmsl calculation
mmsl_year_ini = 1947
mmsl_year_end = 2018
3.3. Monthly Mean Sea Level#
# --------------------------------------
# Calculate SLR using linear regression
WL['time'] = WL['time'].dt.round('H')
time = WL.time.values[:]
wl = WL.values[:] * 1000 # (m to mm)
# MOVE TIME SERIES HALF A YEAR BACK
time = time - pd.Timedelta(days=366/2)
lr_time = np.array(range(len(time))) # for linregress
mask = ~np.isnan(wl) # remove nans with mask
slope, intercept, r_value, p_value, std_err = linregress(lr_time[mask], wl[mask])
slr = intercept + slope * lr_time
# Plot tide with SLR
Plot_Tide_SLR(time, wl, slr);

# --------------------------------------
# remove SLR and runmean from tide
tide_noslr = wl - slr
# calculate tide running mean
time_window = 365*24*3
runm = running_mean(tide_noslr, time_window, 'mean')
# remove running mean
tide_noslr_norunm = tide_noslr - runm
# store data
TNSR = xr.DataArray(tide_noslr_norunm, dims=('time'), coords={'time':time})
# Plot tide without SLR and runm
Plot_Tide_RUNM(time, tide_noslr, runm);
running_mean: input data contain NaNs!!
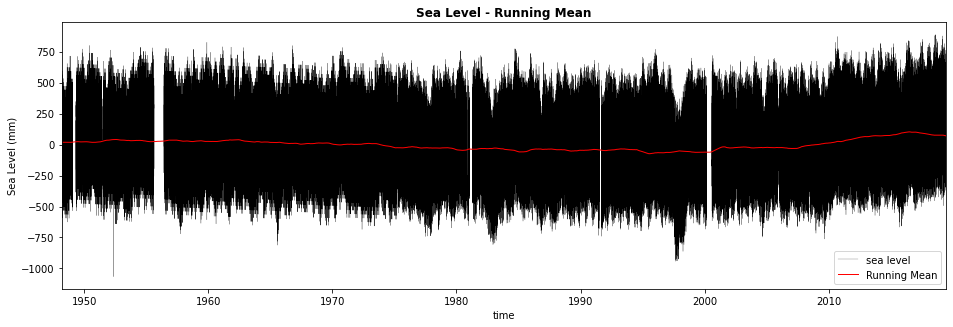
# --------------------------------------
# calculate Monthly Mean Sea Level (mmsl)
MMSL = monthly_mean(TNSR, mmsl_year_ini, mmsl_year_end)
# fill nans with interpolated values
p_nan = np.isnan(MMSL.data_mean)
MMSL.data_mean[p_nan]= np.interp(MMSL.time[p_nan], MMSL.time[~p_nan], MMSL.data_mean[~p_nan])
mmsl_time = MMSL.time.values[:]
mmsl_vals = MMSL.data_mean.values[:]
# Plot tide and mmsl
Plot_Tide_MMSL(TNSR.time, TNSR.values, mmsl_time, mmsl_vals);
# store historical mmsl
save_nc(MMSL,mmsl_hist_file)

3.4. Monthly Mean Sea Level - Principal Components#
The annual PCs are passed to a monthly resolution
# --------------------------------------
# SST Anual Weather Types PCs
PCs = np.array(SST_KMA.PCs.values)
PC1, PC2, PC3 = PCs[:,0], PCs[:,1], PCs[:,2]
PCs_years = [int(str(t).split('-')[0]) for t in SST_KMA.time.values[:]]
# MMSL PCs calculations: cut and pad it to monthly resolution
ntrs_m_mean = np.array([])
ntrs_time = []
MMSL_PC1 = np.array([])
MMSL_PC2 = np.array([])
MMSL_PC3 = np.array([])
for c, y in enumerate(PCs_years):
pos = np.where(
(mmsl_time >= np.datetime64('{0}-06-01'.format(y))) &
(mmsl_time <= np.datetime64('{0}-05-29'.format(y+1)))
)
if pos[0].size:
ntrs_m_mean = np.concatenate((ntrs_m_mean, mmsl_vals[pos]),axis=0)
# TODO check for 0s and nans in ntrs_m_mean?
ntrs_time.append(mmsl_time[pos])
MMSL_PC1 = np.concatenate((MMSL_PC1, np.ones(pos[0].size)*PC1[c]),axis=0)
MMSL_PC2 = np.concatenate((MMSL_PC2, np.ones(pos[0].size)*PC2[c]),axis=0)
MMSL_PC3 = np.concatenate((MMSL_PC3, np.ones(pos[0].size)*PC3[c]),axis=0)
ntrs_time = np.concatenate(ntrs_time)
# Parse time to year fraction for linear-regression seasonality
frac_year = np.array([d2yf(x) for x in ntrs_time])
3.5. Monthly Mean Sea Level - Multivariate-linear Regression Model#
# --------------------------------------
# Fit linear regression model
def modelfun(data, *x):
pc1, pc2, pc3, t = data
return x[0] + x[1]*pc1 + x[2]*pc2 + x[3]*pc3 + \
np.array([x[4] + x[5]*pc1 + x[6]*pc2 + x[7]*pc3]).flatten() * np.cos(2*np.pi*t) + \
np.array([x[8] + x[9]*pc1 + x[10]*pc2 + x[11]*pc3]).flatten() * np.sin(2*np.pi*t) + \
np.array([x[12] + x[13]*pc1 + x[14]*pc2 + x[15]*pc3]).flatten() * np.cos(4*np.pi*t) + \
np.array([x[16] + x[17]*pc1 + x[18]*pc2 + x[19]*pc3]).flatten() * np.sin(4*np.pi*t)
# use non-linear least squares to fit our model
split = 160 # train / validation split index
x0 = np.ones(20)
sigma = np.ones(split)
# select data for scipy.optimize.curve_fit
x_train = ([MMSL_PC1[:split], MMSL_PC2[:split], MMSL_PC3[:split], frac_year[:split]])
y_train = ntrs_m_mean[:split]
res_lsq, res_cov = curve_fit(modelfun, x_train, y_train, x0, sigma)
3.6. Train and test model#
# Check model at fitting period
yp_train = modelfun(x_train, *res_lsq)
Plot_Validate_MMSL_tseries(ntrs_time[:split], ntrs_m_mean[:split], yp_train);
Plot_Validate_MMSL_scatter(ntrs_m_mean[:split], yp_train);


# Check model at validation period
x_val = ([MMSL_PC1[split:], MMSL_PC2[split:], MMSL_PC3[split:], frac_year[split:]])
yp_val = modelfun(x_val, *res_lsq)
Plot_Validate_MMSL_tseries(ntrs_time[split:], ntrs_m_mean[split:], yp_val);
Plot_Validate_MMSL_scatter(ntrs_m_mean[split:], yp_val);


# Parameter sampling (generate sample of params based on covariance matrix)
n_sims = 10
theta_gen = res_lsq
theta_sim = multivariate_normal(theta_gen, res_cov, n_sims)
# Check model at validation period
yp_valp = np.ndarray((n_sims, len(ntrs_time[split:]))) * np.nan
for i in range(n_sims):
yp_valp[i, :] = modelfun(x_val, *theta_sim[i,:])
# 95% percentile
yp_val_quant = np.percentile(yp_valp, [2.275, 97.275], axis=0)
Plot_Validate_MMSL_tseries(ntrs_time[split:], ntrs_m_mean[split:], yp_val, mmsl_pred_quantiles=yp_val_quant);

# Fit model using entire dataset
sigma = np.ones(len(frac_year))
x_fit = ([MMSL_PC1, MMSL_PC2, MMSL_PC3, frac_year])
y_fit = ntrs_m_mean
res_lsq, res_cov = curve_fit(modelfun, x_fit, y_fit, x0, sigma)
# obtain model output
yp = modelfun(x_fit, *res_lsq)
# Generate 1000 simulations of the parameters
n_sims = 1000
theta_gen = res_lsq
param_sim = multivariate_normal(theta_gen, res_cov, n_sims)
# Check model
yp_p = np.ndarray((n_sims, len(ntrs_time))) * np.nan
for i in range(n_sims):
yp_p[i, :] = modelfun(x_fit, *param_sim[i,:])
# 95% percentile
yp_quant = np.percentile(yp_p, [2.275, 97.275], axis=0)
Plot_Validate_MMSL_tseries(ntrs_time, ntrs_m_mean, yp, mmsl_pred_quantiles=yp_quant);
# Save model parameters to use in climate change
model_coefs = xr.Dataset({'sim_params' : (('n_sims','n_params'), param_sim)})
save_nc(model_coefs, model_coefs_file)

3.7. Monthly Mean Sea Level - Prediction#
# --------------------------------------
# Predict 1000 years using simulated PCs (monthly time resolution)
# get simulation time as year fractions
PCs_sim_time = SST_PCs_sim_m.time.values[:]
frac_year_sim = np.array([d2yf(x) for x in PCs_sim_time])
# solve each PCs simulation
y_sim_n = np.ndarray((len(SST_PCs_sim_m.n_sim), len(frac_year_sim))) * np.nan
for s in SST_PCs_sim_m.n_sim:
PCs_s_m = SST_PCs_sim_m.sel(n_sim=s)
MMSL_PC1_sim = PCs_s_m.PC1.values[:]
MMSL_PC2_sim = PCs_s_m.PC2.values[:]
MMSL_PC3_sim = PCs_s_m.PC3.values[:]
# use linear-regression model
x_sim = ([MMSL_PC1_sim, MMSL_PC2_sim, MMSL_PC3_sim, frac_year_sim])
y_sim_n[s, :] = modelfun(x_sim, *param_sim[s,:])
# join output and store it
MMSL_sim = xr.Dataset(
{
'mmsl' : (('n_sim','time'), y_sim_n / 1000), # mm to m
},
{'time' : PCs_sim_time}
)
print(MMSL_sim)
# save
save_nc(MMSL_sim, mmsl_sim_file, safe_time=True)
<xarray.Dataset>
Dimensions: (n_sim: 100, time: 984)
Coordinates:
* time (time) datetime64[ns] 2019-06-01 2019-07-01 ... 2101-05-01
Dimensions without coordinates: n_sim
Data variables:
mmsl (n_sim, time) float64 0.01943 0.02091 0.03767 ... 0.07367 0.04747
# Plot mmsl simulation
plot_sim = 0
y_sim = MMSL_sim.sel(n_sim=plot_sim).mmsl.values[:] * 1000 # m to mm
t_sim = MMSL_sim.sel(n_sim=plot_sim).time.values[:]
# Plot mmsl prediction
Plot_MMSL_Prediction(t_sim, y_sim);
# compare model histograms
Plot_MMSL_Histogram(ntrs_m_mean, y_sim);


# compare model histograms for all simulations
y_sim = MMSL_sim.mmsl.values[:].flatten() * 1000 # m to mm
Plot_MMSL_Histogram(ntrs_m_mean, y_sim);


