Construcción con Geogebra

Dibujamos con Geogebra el triángulo de Sierpinski:

Acciones	Pasos a realizar
Abrir Geogebra	Hacer doble clic sobre el icono
Modificar el aspecto de la vista gráfica	Elegir Menú Edita. Desmarcar opción ejes. Elegir Menú Edita. Desmarcar opción cuadrícula.
Definir un triángulo de lado el segmento AB	Teclear en el campo entrada: A=(-3,0) Teclear en el campo entrada: B=(0,3) Teclear en el campo entrada: T = Polígono[A, B, 3]
Generar los triángulos correspondientes a la etapa 1	Elegimos la herramienta Punto Medio: Marcamos los puntos A y B. Se obtiene D. Marcamos los puntos A y C. Se obtiene E. Marcamos los puntos B y C. Se obtiene F. Nota: También se puede obtener el punto medio de otros dos, P y Q, tecleando PuntoMedio[P,Q]. Creamos el triángulo t1 cuyos vértices son D, E y F: Seleccionamos la herramienta Triángulo. Hacemos clic en los puntos D, E, F, D. 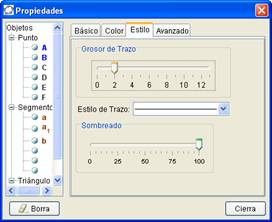Rellenamos el triángulo de blanco seleccionándolo y, en Propiedades, eligiendo color blanco y Sombreado 100%.
Modificar el dibujo para mostrar solo puntos y triángulos	Elegir del menú Edita la opción Propiedades y desmarcar “Muestra Objeto” y “Muestra Rótulo” de los elementos que se desee ocultar.
Desplazar los puntos de la etapa anterior	Hacer clic sobre los puntos A1…A8 en la lista de objetos dependientes y redefinirlos sumándoles (0, 2/3·L).
Crear herramienta Sierpinski1	Elegir del menú Herramientas “Creación de Herramientas Nueva”. En Objetos de Salida incluir D, E, F, r1. En Objetos de Entrada incluir A y B. En Nombre e Icono elegir “Sierpinski1”. Pulsar el botón Concluido.

Generar el triángulo de Sierpinski de orden 2, 3 y 4

◀ Anterior Siguiente ▶