Copo de nieve
Si el proceso se realiza sobre los tres lados de un triángulo equilátero se obtiene la curva copo de nieve o de Knoch.
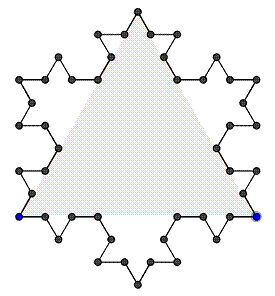
El área del copo de Koch es finita y su contorno (frontera) es infinita.
| Etapa | Área | Perímetro |
|---|---|---|
| $0$ | $\frac{L^2\sqrt{3}}{4}$ | $3L$ |
| $1$ | $\frac{L^{2}\sqrt{3}}{4}+\frac{L^{2}\sqrt{3}}{4\cdot 3}$ | $3L+L$ |
| $2$ | $\frac{L^{2}\sqrt{3}}{4}+\frac{L^{2}\sqrt{3}}{4\cdot 3}+\frac{L^{2}\sqrt{3}}{4\cdot 3^{2}}$ | $3L+L+\frac{4}{3}L$ |
| $3$ | $\frac{L^{2}\sqrt{3}}{4}+\frac{L^{2}\sqrt{3}}{4\cdot 3}+\frac{L^{2}\sqrt{3}}{4\cdot 3^{2}}+\frac{L^{2}\sqrt{3}}{4\cdot 3^{3}}$ | $3L+L+\frac{4}{3}L+\frac{4^{2}}{3^{2}}L$ |
| $4$ | $\frac{L^{2}\sqrt{3}}{4}+\frac{L^{2}\sqrt{3}}{4\cdot 3}+\frac{L^{2}\sqrt{3}}{4\cdot 3^{2}}+\frac{L^{2}\sqrt{3}}{4\cdot 3^{3}}+\frac{L^{2}\sqrt{3}}{4\cdot 3^{4}}$ | $3L+L+\frac{4}{3}L+\frac{4^{2}}{3^{2}}L+\frac{4^{3}}{3^{3}}L$ |
| … | … | … |
| $\frac{2\sqrt{3}}{5}L^{2}$ | infinita |