Juan M. López
Non-equilibrium Statistical Mechanics and Complex Systems


- Surface coarsening. Numerical simulations of surface growth in the presence of quenched disorder [Physical Review E 76, 011603 (2007)]
- Order parameter at the synchronization transition of two coupled spatially extended nonlinear systems. On the right the transition is continuous (directed percolation), while on the left the transition is discontinuous [Physical Review E 71 (Rapid Comm.), 055203(R) (2005)]
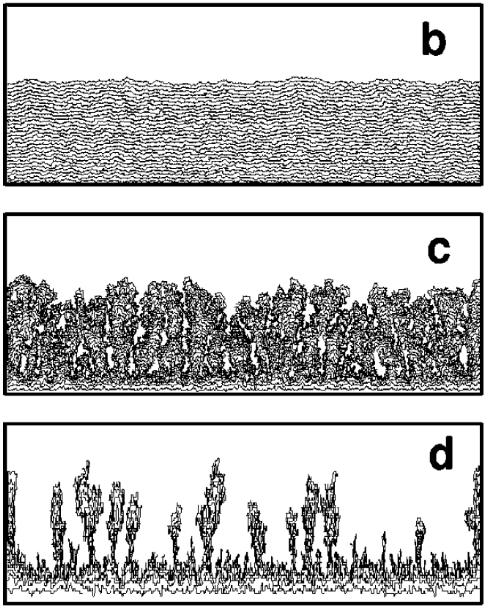
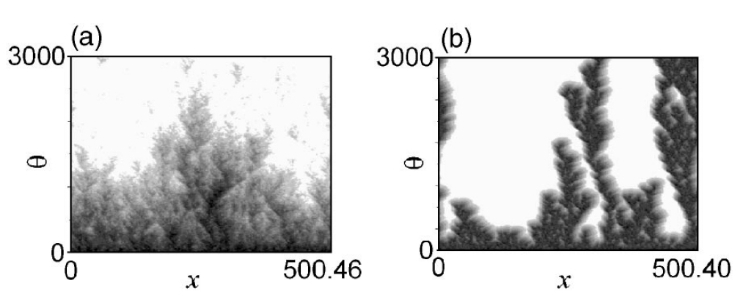
- Patterns in a model of fungal growth. Images from top to bottom correspond to decreasing food supply so that cells strive for dividing [Physical Review E 65, 021903 (2002)]
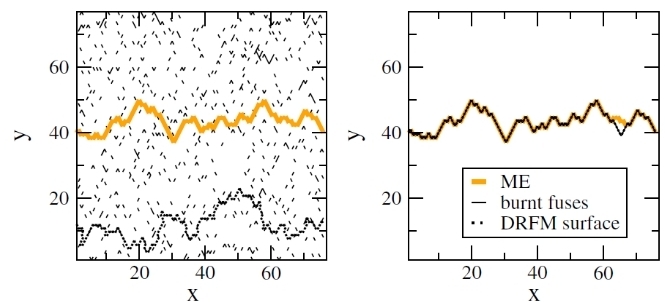
- Simulations of ductile fracture with the Ductile Random Fuse Model (DRFM). On the left the material is quasi-brittle, damage is diffuse. On the right, the material is extremely ductile and the crack localizes around the minimum energy surface across the system [Physical Review Letters 105, 155502 (2010)]
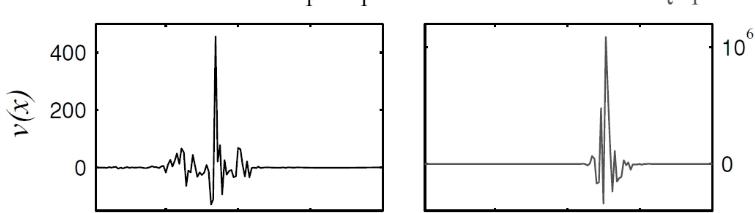
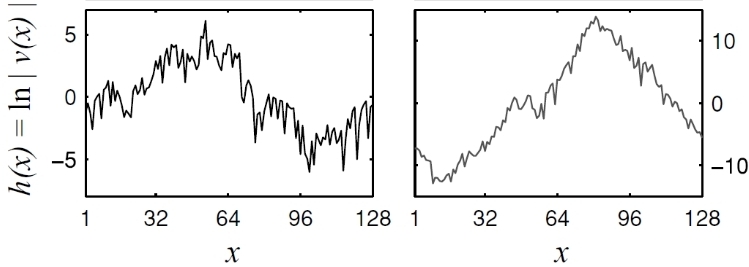
- Lyapunov vectors in spatially extended systems are strongly localized objects. LV (left) and Singular vector (right) are plotted for a Lorenz 96 system. Under a logarithmic transform LVs can be generically treated as rough surfaces (bottom panels) [Tellus 62A, 10 (2010)]
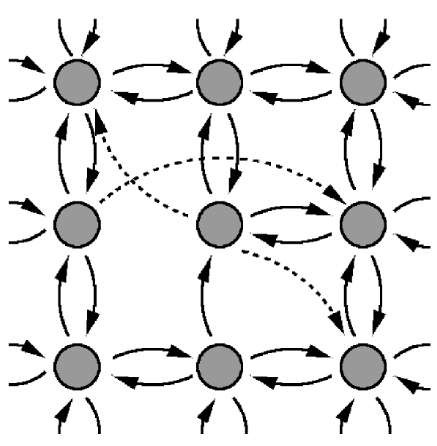
- Sketch of a directed small-world network constructed from a square regular lattice in d=2. Arrows indicate the direction of the corresponding link. Dotted lines represent rewired links. This network serves as a simple model for opinion spreading [Physical Review Letters 88, 048701 (2002)]
- All images above are my own work. You can use by citing the original source.
Surface growth and kinetic roughening
Interfaces, fronts, and surfaces appear everywhere in Nature and often play a significant role in the exchange of energy, heat, or matter between the system and the environment or different parts of the system. The range of length scales at which surfaces appear covers several orders of magnitude in length scales ranging from nanometric scales all the way up to the length scales in our everyday experience. Think of the frontier separating two immiscible fluid phases, sand dunes, domain-walls in magnets, the cell membrane, crack fronts in solids, fluids in porous media, electrodeposition, and so on. A particularly important example of surfaces with great technological applications nowadays appear during thin-film growth at nanoscale (~10-9 m) when atoms adhere at substrates via molecular-beam epitaxy, chemical-vapor deposition, ion-sputtering, and other techniques used in modern nanoscience to build many devices as semiconductors, logical gates, lasers, chemical catalysis and filters ...
I am working on the theoretical description of surfaces in several of the above mentioned contexts. It turns out that coarse-grained models that describe surface growth can often be constructed solely from symmetry principles. We are interested in the scaling properties of these roughening processes that typically lead to fractal, scale-invariant in space and time, surfaces. This involves the use of scaling theory and renormalization group concepts together with numerical simulations.
Statistical mechanics of space-time chaos
Purely deterministic nonlinear dynamical systems often exhibit chaos in space and time. Even if these systems are fully deterministic, the lack of predictability of chaotic trajectories in very high dimensions provides some elements of randomness, at least at certain level of description. Therefore, in a coarse-grained description statistical mechanics can offer useful tools to treat space-time chaos.
Our research in this topic is partially inspired by problems that arise in dynamical models for the atmosphere, Lyapunov vectors and their use in predictability studies. In particular, the problem of ensemble prediction systems and generation of adequate initial perturbations for forecasting are within our scope. In this line of research we have a close collaboration with the Meteorology and Climate Change group in our institute. Therfore, part of work in this line of research is oriented toward the geophysics comunity while more theoretical studies of chaos in dynamical systems is published in general physics journals.
Avalanches, fluctuations, and intermittent behaviour in complex systems
Many nonequilibrium systems respond in the form of avalanches or intermittent bursts in response to a slow external driving. This behaviour is typical of complex systems involving many degrees of freedom and nonlinear interactions. Examples can be found in the acoustic emission or crackling noise that appears in materials under loading, earthquakes, motion of domain-walls in disordered ferromagnets, ... This is a highly non trivial dynamics that is still far from being fully understood. What does it make a noisy system with solely local interactions to organize into a state with critical properties including long range temporal correlations and scale-free distributions of activity?
Plasticity and fracture in disordered media
We are studying mesoscopic models of plastic response and fracture of materials. Despite the huge differences in material properties, the response of heterogeneous or disordered materials to loading exhibits some common features including power-law distributions of shear avalanches, damage localization, shear bands, roughening exponents of the fracture crack surfaces, ... Our research is aimed at uncovering the basic ingredients that provide a theoretical explanation of these experimental observations.
![]()