Tema 10. Herramientas avanzadas

Tabla de Contenidos

1. Herramientas avanzadas
   1. Grabar y ejecutar macros
   2. Crear un botón
   3. Editar una macro
   4. Almacenando macros
   5. Campos de control de formularios
   6. Optimizar con Solver
   7. Revisar ortografía
   8. Incorporar extensiones

Optimizar con Solver

Vemos su funcionamiento con un ejemplo.

En este caso se trata de encontrar cuánto deben valer:

• x=número de viajeros fumadores
• y=número de viajeros no fumadores

para que el valor de P=100x+60y sea máximo. Estos valores x, y no son cualesquiera, tienen que cumplir unas restricciones:

• x e y deben ser mayor o igual que 0 (el número de viajeros no puede ser un número negativo)
• el peso que lleven los viajeros no puede ser mayor de 3000 kg, es decir, 50x+20y debe ser menor o igual que 3000
• el número de viajeros no puede exceder del número máximo de plazas del autobús, es decir, x+y debe ser menor o igual a 90

Resolveremos este problema con ayuda de Ooo Calc. El primer paso es construir una hoja de cálculo como la siguiente en la que en C3 y C4 se identificarán con las variables x e y anteriormente definidas.

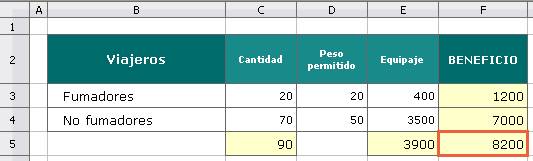
Las fórmulas que se han incluido son las siguientes

• Celda C5: =C3+C4 (permite calcular el número total de viajeros)
• Celda E3: =C3*D3 (permite calcular el equipaje de los viajeros fumadores)
• Celda E4: =C4*D4 (permite calcular el equipaje de los viajeros no fumadores)
• Celda E5: =E3+E4 (permite calcular el equipaje de total de todos los viajeros)
• Celda F3: =C3*60 (permite calcular el beneficio asociado a los viajantes fumadores)
• Celda F4: =C4*100 (permite calcular el beneficio asociado a los viajantes no fumadores)
• Celda F5: =F3+F4 (permite calcular el beneficio total por la venta de todos los billetes).

En primer lugar debemos observar que lo que tratamos de hacer máximo es el valor de la celda F5, esta celda es la celda objetivo. La solución del problema pasa por elegir unos valores de C3 y C4 para conseguir que la celda objetivo sea máxima. Como hemos comentado anteriormente, estos valores no son libres ya que deben cumplir ciertas condiciones que ahora se expresarán como:

• C3 y C4 deben ser positivos o nulos
• C5, el número de viajeros, no debe ser superior a 90
• E5, el equipaje total, no debe superar a 3000 kg

Para resolver este problema con OOo Calc elegimos la opción Solver del menú Herramientas incluyendo en el cuadro la función objetivo y las restricciones que hemos indicado y que se muestran en la figura siguiente:

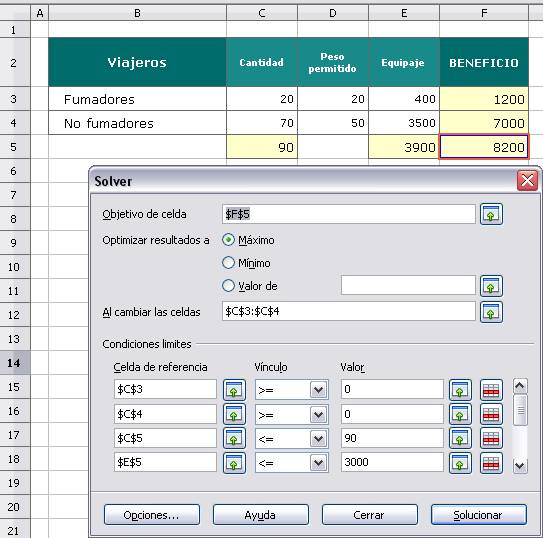
Cuando se haga clic en el botón Solucionar, OOo Calc nos dará la solución de este problema; en el ejemplo seguido se obtendrá que el beneficio es 7000€ admitiendo 50 viajeros fumadores y 40 no fumadores.

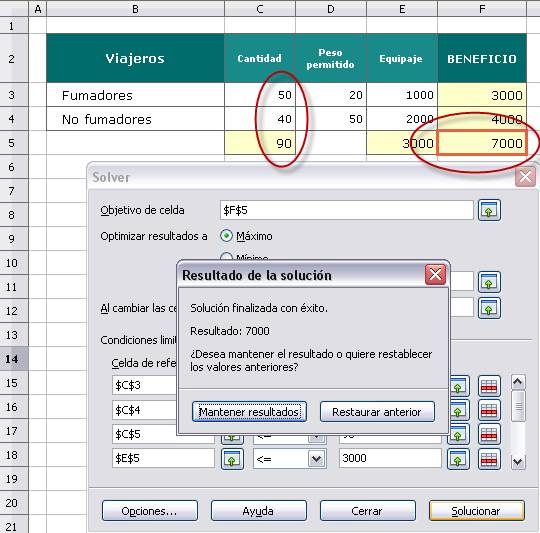
El botón Opciones... del cuadro de diálogo Solver puede ayudar, en algunos casos, a encontrar la solución. Los cuatro ajustes que se pueden hacer es:

• Asume variables como no negativo En nuestro ejemplo esta opción tendría sentido ya que el número de viajeros no puede ser nunca negativo.
• Asumir variables como enteros. También es claro que en nuestro caso el número de viajeros fumadores o no deben ser números enteros por lo que podríamos elegir esta opción antes de hacer clic en el botón Solucionar.
• Nivel épsilon Al hacer doble clic sobre este botón se puede cambiar el grado de aproximación a la solución.
• Límite de tiempo. Aunque para ejemplos sencillos el valor que tiene asignado por defecto es suficiente, 100 segundos, también se puede cambiar.

1

Autoevaluación A la hora de modelizar un problema lineal a optimizar con la herramienta Solver he de pensar en... a) La fórmula que dará el resultado máximo o mínimo en la celda objetivo (a calcular con la herramienta Solver) y las restricciones que se detallan en el enunciado sobre las variables que afectan al resultado de la celda objetivo, de tal forma que al ejecutar la herramienta, Calc encuentra el resultado entre todos los posibles valores de las variables (dentro del área delimitada por las restricciones, ver animación). b) La fórmula que dará el resultado exacto, máximo o mínimo como la celda objetivo, y también en las restricciones o condiciones límites que se detallan en el enunciado sobre las variables (relacionándose o no) que afectan al resultado de la celda objetivo, donde una o varias celdas de referencia (que pueden contener números o fórmulas) tiene un vínculo con un determinado valor, p.e. es mayor o igual a 5, de tal forma que al ejecutar la herramienta, Calc encuentra el resultado entre todos los posibles valores de las variables (dentro del área delimitada por las restricciones, ver animación). c) La celda con el resultado exacto, máximo o mínimo en la celda objetivo, y también en las restricciones o condiciones límites que se detallan en el enunciado sobre las variables que afectan al resultado de la celda objetivo, donde una o varias celdas de referencia (que sólo pueden ser un número) tienen un vínculo con un determinado valor, p.e. es mayor o igual a 5, de tal forma que al ejecutar la herramienta, Calc encuentra el resultado entre todos los posibles valores de las variables (dentro del área delimitada por las restricciones, ver animación). Exacto, eso es lo que hay que tener en cuenta... Experimenta un poco más con la herramienta Solver y te darás cuenta de que pasaste por alto algún aspecto importante.Tu respuesta ha sido guardada.