Métodos Numéricos
Ejercicios prácticos con Matlab
Autores:
Elena E. Álvarez Saiz
Código JavaScript para el libro:
Joel Espinosa Longi,
IMATE, UNAM.
Recursos interactivos:
DescartesJS, WebSim
Videos: Math-GPT
Fuentes: Lato y
UbuntuMono
Imagen de portada: ilustración generada por
Pollinations AI
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/
ISBN: 978-84-10368-24-8

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No
Comercial-Compartir Igual.
Los métodos numéricos son una herramienta esencial para quienes ejercen la ingeniería, ya que permiten resolver problemas complejos que a menudo no tienen una solución analítica simple. Estas técnicas posibilitan abordar situaciones reales mediante aproximaciones, convirtiéndose en un recurso indispensable en la práctica profesional.
Este libro está diseñado para quienes deseen adquirir una comprensión de los métodos numéricos para el cálculo de raíces de funciones no lineales, la aproximación de funciones mediante polinomios, la integración numérica y la resolución de ecuaciones diferenciales ordinarias.
Este libro ofrece:
La orientación de este libro no solo pretende facilitar el aprendizaje, sino también despertar el interés por profundizar en el estudio de los métodos numéricos. La idea es acompañar al lector a través de una exposición clara y ordenada, donde cada contenido ayude a construir una base sólida que conecte los conceptos teóricos con su aplicación práctica.
Este libro toma como punto de partida los apuntes del profesor Eduardo Casas Rentería de la Universidad de Cantabria
La estructura del libro se organiza en seis temas, que van desde los conceptos básicos hasta aplicaciones más avanzadas. El primer tema introduce los métodos numéricos y el uso de Matlab/Octave, sentando las bases para el aprendizaje y la implementación computacional. El segundo aborda la aritmética computacional básica, destacando los principios fundamentales para trabajar en un entorno digital. En el tercer tema se estudia la resolución aproximada de ecuaciones no lineales, explorando distintos métodos para encontrar raíces de funciones. El cuarto tema se centra en la aproximación de funciones mediante polinomios, una herramienta esencial en el análisis numérico. El quinto capítulo trata la integración numérica, presentando técnicas para calcular integrales de forma aproximada. Finalmente, se introduce la resolución de ecuaciones diferenciales ordinarias, ofreciendo métodos numéricos para su aproximación.
Soy consciente de que este libro puede contener algunas erratas o inconsistencias por lo que se anima a los lectores a compartir cualquier observación o corrección que consideren necesaria. Sus aportaciones serán de gran ayuda para mejorar futuras ediciones y asegurar que este recurso sea cada vez más útil.
Finalmente, quiero agradecer a la Red Educativa Digital Descartes y, de manera especial, a Juan Guillermo Rivera Berrío por compartir generosamente su conocimiento. Su experiencia y su compromiso con la educación han sido fundamentales para enriquecer este trabajo.

El análisis numérico es una rama de las matemáticas que se ocupa de estudiar métodos y algoritmos para encontrar soluciones aproximadas a problemas que no pueden resolverse de manera exacta mediante técnicas analíticas tradicionales. Algunos de estos problemas incluyen la resolución de ecuaciones algebraicas y diferenciales, el cálculo de integrales o el tratamiento de sistemas de ecuaciones, tanto lineales como no lineales.
Al estudiar métodos numéricos, es importante considerar los siguientes aspectos:
Para ilustrar la aplicación de los métodos numéricos en problemas reales, se considera el caso de un sistema de baterías conectado a un panel solar que genera electricidad a lo largo del día. Se quiere modelar cómo la batería se carga con el tiempo, sabiendo que:
La ecuación que podría modelizar cómo se almacena la energía en la batería podría ser la siguiente ecuación diferencial ordinaria (EDO):
$$ \frac{dE}{dt} = P_{solar}(t) - kE(t) $$donde:
Se recurre a técnicas numéricas para obtener una solución aproximada considerando los siguientes datos y parámetros:
La gráfica de la Figura 1.1 muestra la evolución de la energía almacenada en la batería en un día (24 horas) en función de la potencia solar disponible, utilizando como método de resolución el método de Euler que se analizará en detalle en el capítulo 6 de este libro. En la gráfica
Se observa cómo la batería se carga durante las horas de sol y comienza a descargarse lentamente debido a las ineficiencias cuando no hay suficiente energía solar disponible.
El ejemplo descrito anteriormente responde a un problema de valor inicial (PVI) que busca encontrar la curva solución de una ecuación diferencial ordinaria de primer orden de la forma $\frac{dy}{dt} = f(t, y)$ con una condición inicial $y(t_0)=y_0$. La solución es la curva $y(t)$ que pasa por el punto $(t_0,y_0)$ y tiene como pendiente de la curva en cualquier punto el valor establecido por la función $f$.
El método de Euler, que se verá en detalle en el capítulo 6, propone aproximar esta curva avanzando paso a paso a través de pequeños saltos en el eje \( x \) moviéndose suavemente por la recta tangente en cada instante ya que $f$ permite calcular la pendiente a la curva en cada punto. En este proceso, se recalcula la dirección en cada paso.
A continuación se detalla el proceso a seguir en este método numérico, que se inicia desde el punto $(t_0,y_0)$.
Se obtendría así una lista de puntos \( (t_0 , y_0) \), \( (t_1 , y_1) \), ... \( (t_n , y_n) \) donde $t_n=t_{n-1}+\Delta t$
En este ejemplo introductorio que se está viendo, el problema de valor inicial es el siguiente,
$$ \frac{dE}{dt} = P_{solar}(t) - kE(t) \,\,\,\,\,\,\,\, E(0)=0$$La aplicación del método de Euler para encontrar la solución de forma numérica consisté en aplicar la siguiente fórmula iterativa
$$ E(n+1) = E(n) + Δt \cdot (P_{solar}(t_n) - k \cdot E(n)) $$donde $Δt$ es el paso de tiempo (1 hora) y $E(n)$ es la energía almacenada en la batería en el instante $n$. Así, es posible calcular la energía almacenada en la batería a lo largo de 24 horas utilizando la potencia solar que varía con el tiempo. Se muestra seguidamente el cálculo de los primeros pasos.
Condición inicial:El proceso continuaría realizando el cálculo para las 24 horas del día de forma similar.
Los errores en métodos numéricos, aunque pequeños al inicio, pueden crecer y afectar gravemente los resultados. Comprenderlos es clave para evitar fallos. A continuación, se muestran ejemplos históricos con consecuencias significativas.
El 25 de febrero de 1991, durante la Guerra del Golfo, una batería de misiles Patriot del ejército estadounidense ubicada en Dharan, Arabia Saudita, falló al intentar interceptar un misil Scud lanzado por las fuerzas iraquíes. El misil impactó en un cuartel del ejército estadounidense, causando la muerte de 28 soldados. Un informe de la entonces Oficina General de Contabilidad, titulado "Patriot Missile Defense: Software Problem Led to System Failure at Dhahran, Saudi Arabia", identificó la causa del fallo: un error aritmético en los cálculos de tiempo del sistema, que provocó un desfase desde el inicio de la operación

Concretamente, el reloj interno del sistema medía el tiempo en décimas de segundo, y este valor se multiplicaba por 10 para obtener el tiempo en segundos. El cálculo se realizaba usando un registro de punto fijo de 24 bits. Como 1/10 tiene una expansión binaria infinita, se representó truncándolo a 24 bits después del punto decimal. Aunque el error de truncamiento era muy pequeño, al multiplicarse por el número grande que representaba el tiempo en décimas de segundo, acabó generando un error apreciable
El Programa Ariane comenzó en 1973 como una iniciativa europea para desarrollar un lanzador propio que asegurara su acceso independiente al espacio. El proyecto se llevó a cabo bajo la supervisión de la Agencia Espacial Europea (ESA, por sus siglas en inglés). Hasta mayo de 2003, el contratista principal fue el Centro Nacional de Estudios Espaciales (CNES) de Francia, momento en el que esta responsabilidad pasó al consorcio europeo EADS (European Aeronautic Defence and Space Company).
La gestión comercial del lanzador Ariane estuvo a cargo de la sociedad Arianespace, creada en 1980, y en su desarrollo y construcción participaron alrededor de 40 compañías europeas. Todos los lanzamientos se realizaban desde el centro espacial de Kourou, en la Guayana Francesa, que disponía de varias plataformas de despegue y contaba con varios cientos de trabajadores de forma permanente.
El 4 de junio de 1996, el cohete Ariane 5 Flight 501, de la Agencia Espacial Europea (ESA), explotó apenas 40 segundos después de su despegue, a una altitud de 3,7 km, tras desviarse de la trayectoria prevista.

El vuelo del Ariane 5 Flight 501 era su primer lanzamiento tras una década de desarrollo, que había supuesto una inversión de más de 7000 millones de euros. Tanto el cohete como su carga estaban valorados en más de 500 millones de euros. La explosión fue provocada por un fallo en el sistema de guiado de la trayectoria, ocurrido 37 segundos después del despegue. La causa del error se localizó en el software encargado de controlar el sistema de referencia inercial (SRI).
En concreto, el fallo se produjo por una excepción al intentar convertir un número en punto flotante de 64 bits —relacionado con la velocidad horizontal del cohete respecto a la plataforma de lanzamiento— en un entero con signo de 16 bits. El problema fue que el valor que se intentaba almacenar superaba el máximo que puede representarse en 16 bits con signo, que es 32.767.
Para más información, se puede consultar
El 23 de agosto de 1991, la plataforma petrolífera Sleipner A, propiedad de la empresa noruega Statoil, se hundió en el mar del Norte a 82 metros de profundidad. El accidente se debió a un error en el modelado numérico de la estructura mediante elementos finitos, que provocó una fuga de agua en uno de los 24 tanques de aire de 12 metros de diámetro, esenciales para la flotabilidad. La plataforma, que soportaba 57.000 toneladas de peso, más 200 personas y 40.000 toneladas de equipamiento, no pudo ser salvada debido a la incapacidad de las bombas de achique para evacuar el agua. El hundimiento supuso un coste estimado de 700 millones de euros
Para modelar los tanques de la plataforma se utilizó el programa NASTRAN, basado en el método de elementos finitos, aplicando una aproximación mediante un modelo elástico lineal. Sin embargo, esta aproximación resultó inadecuada y subestimó en un 47 % los esfuerzos que debían soportar las paredes de los tanques. Como consecuencia, algunas paredes fueron diseñadas con un grosor insuficiente.
Un análisis posterior al accidente, realizado mediante el método de elementos finitos de forma más precisa, demostró que el diseño de la plataforma provocaría fugas en algunos de los tanques cuando estuviera sobre una lámina de agua de 62 metros de profundidad. La fuga real se produjo cuando la plataforma se encontraba sobre 65 metros de agua, lo que confirmó la causa del fallo.

Para desarrollar y resolver los ejercicios y ejemplos propuestos en este libro, se utilizará como herramienta principal de cálculo el programa Matlab. Su interfaz intuitiva y su amplia biblioteca de funciones lo convierten en una herramienta ideal para ilustrar conceptos matemáticos, realizar simulaciones y aplicar métodos computacionales en un entorno práctico.
Matlab es un acrónimo de "Matrix Laboratory", lo que refleja su origen como una herramienta diseñada para trabajar principalmente con matrices. Con el tiempo, el programa ha evolucionado para convertirse en un entorno de programación de alto nivel que permite realizar cálculos numéricos, análisis de datos, simulaciones, desarrollo de algoritmos y visualizar información.
Aunque Matlab es un software de pago, también se puede utilizar el software libre y gratuito Octave, que es compatible en muchos de sus comandos. Para facilitar la ejecución del código propuesto en los ejemplos y ejercicios, se pueden utilizar los siguientes enlaces sin necesidad de realizar ninguna instalación:
A continuación, se resumen las principales características de Matlab/Octave necesarias para seguir y comprender los ejemplos de los próximos capítulos. Para una explicación más detallada, se recomienda consultar la documentación oficial o la bibliografía recomendada
La ventana de Matlab muestra un escritorio dividido en varias partes:
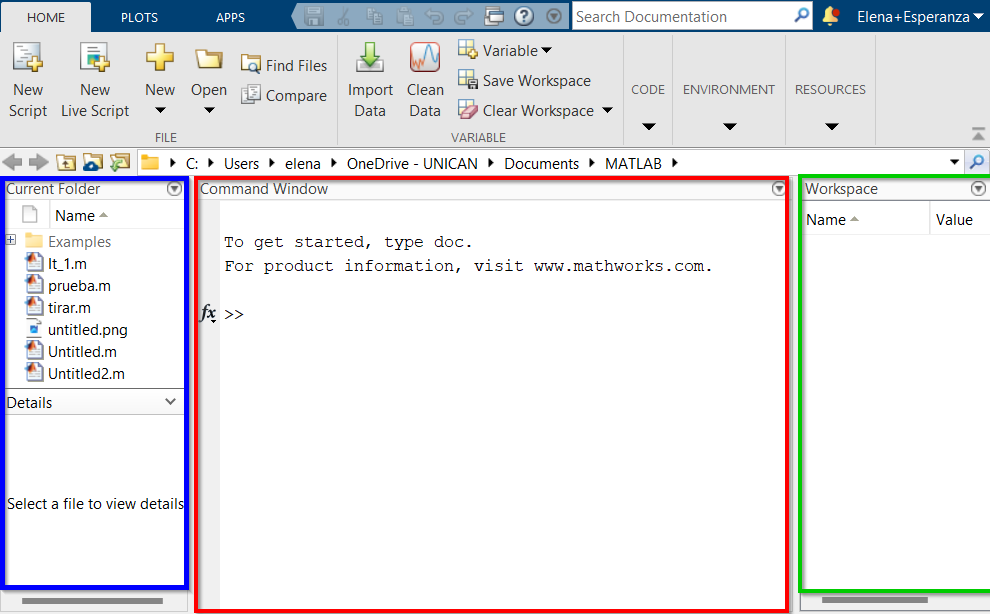
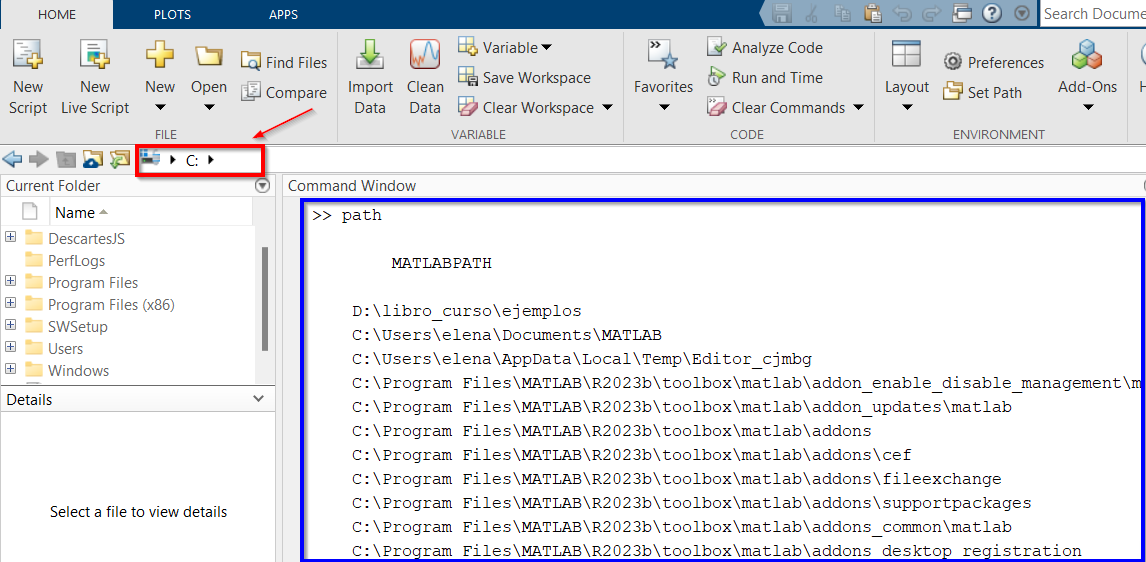
Cuando se guarda el código en un archivo y se quiere utilizar más adelante, es necesario indicar al programa su ubicación. Matlab tiene preconfigurada la ruta donde almacena sus funciones nativas y las de los paquetes incluidos. Sin embargo, si se trabaja con archivos propios, se debe asegurar que el programa pueda acceder a ellos correctamente.
Matlab busca funciones y scripts en los directorios especificados por el comando path. El
primero de ellos es siempre el especificado en el diálogo
Current Directory.
En la figura aparece marcado en rojo el directorio actual. Tecleando el comando
path en la ventana de comandos puede ver el listado de directorios
activos.
Desde la ventana de comandos, se puede utilizar help. para obtener ayuda sobre la sintásis de un determinado comando.
help nombreDelComando >>help plot
Además, desde el menú help, se puede acceder a la ayuda de MathWorks en el caso de Matlab.
En Matlab/Octave, es sencillo crear variables, basta asignar un valor al nombre de la variable. Las variables se almacenan en la memoria y pueden contener números, matrices, cadenas de texto, entre otros. El contenido de una variable se puede recuperar y modificar a lo largo de una sesión de trabajo.
Se detallan a continuación algunas reglas a tener en cuenta a la hora de definir los nombres de las variables:
modulo2 es un nombre
válido, pero no lo es 2modulo.
Modulo es distinta de la variable
modulo.
modulo1 es un nombre de variable válido, pero no lo es
modulo 1.
ans, pi, Inf, i, j, ... . Para obtener una lista de palabras
reservadas teclea en la venta de comando iskeyword().
Un ejemplo de declaración de variable:
x=5; % x es una variable escalar
x=x+6; % El valor de x es 11
Las variables creadas desde la línea de comandos pertenecen al espacio de trabajo (workspace).
Matlab ignora cualquier texto que vaya precedido por el símbolo %, por
lo tanto, este símbolo sirve para incluir comentarios. Los ejemplos que siguen ilustran algunas características de las variables.
>> x=5; 2*x; y=x^2; x=y/x;
El comando format en Matlab/Octave se utiliza para controlar la forma en
que el programa muestra los números en la ventana de comandos. No cambia la precisión interna de
los cálculos, solo afecta a la presentación de los resultados. Aquí tienes algunos de los modos más
comunes de este comando al escribir el número $\pi$.
format short |
4 dígitos después del punto decimal | 3.1416 |
format long |
15 dígitos después del punto decimal | 3.141592653589793 |
format shortEng |
Notacion decimal con 4 dígitos | 3.1416e+00 |
format longEng |
Notacion técnica larga | 3.14159265358979e+000 |
Matlab/Octave permite realizar operaciones aritméticas básicas de manera directa. Las operaciones estándar incluyen suma (+), resta (-), multiplicación (*), división (/) y exponenciación (^). Por ejemplo,
x = 4; y = x + 3; % Suma
z = x * 2; % Multiplicación
A= 2*(x + z); % El valor de A es 24
Las expresiones se evalúan de izquierda a derecha, la potencia tiene el orden de prioridad mayor, seguido del producto y la división (ambas
tienen la misma prioridad) y por último la suma y la resta (con igual prioridad entre ellas). Para alterar este orden se deben introducir adecuadamente paréntesis. Por ejemplo,
x= 2+3^4/2; % x toma el valor 2+81/2
B =2+3^(4/2); % B toma el valor 11=2+3^2
A continuación se presentan ejemplos para practicar operaciones aritméticas y comprender la jerarquía de operadores.
Un script es un archivo que contiene un conjunto de comandos de Matlab/Octave que se ejecutan en orden. El nombre del archivo, por ejemplo nombre.m , debe tener una secuencia de caracteres válidos sin espacios y extensión .m.
También se puede crear un guión desde el editor de Matlab/Octave eligiendo el menú New Script.

Algunas funciones sencillas pueden definirse con una única instrucción en la ventana de comandos mediante lo que se llaman funciones anónimas. Basta establecer su nombre, los argumentos de los que dependen separados por comas y los comandos que permiten definirla.
nombre_Funcion=@(argumentos) expresion_Funcion
Por ejemplo, para definir la función que calcula el área de un rectángulo a partir de su base y altura, habrá que escribir el código siguiente.
>>area_rectangulo=@(b,h) b*h
>>valor=area_rectangulo(4,3)
valor=
12Los vectores en Matlab/Octave permiten almacenar secuencias de elementos que pueden disponerse como una fila o como una columna.
punto_inicial:paso:punto_final
Para generar un vector que comience en 2, avance de 2 en 2 y no supere 9, basta escribir el código siguiente.
>>v=4:2:9 &Devuelve: v=[4 6 8]linspace(valor_inicial,valor_final,num_puntos)
Por ejemplo, para generar un vector fila de 7 elementos equiespaciados siendo el primer valor 2 y el último 3 se deberá escribir:
>>v=linspace(2,3,7)
v=[2.0000 2.1667 2.3333 2.5000 2.6667 2.8333 3.0000]
A continuación se presenta un ejemplo que ilustra diversas formas de definir un vector.
Una matriz es una colección de valores en filas y columnas. Cada fila se separa con un punto y coma (;) y los elementos de una fila se separan con espacios o comas (,). Por ejemplo,
M = [1 2 3; 4 5 6; 7 8 9]; % Es una matriz 3x3
M = [1 2 3; 4 5 6]; % Matriz 2x3, 2 filas y 3 columnas
Se muestra cómo generar algunas matrices especiales.
Matriz de ceros
zeros(numFilas,numColumnas)
% Ejemplo: una matriz 4x3 de ceros
>>zeros(4,3)
Matriz de unos
ones(numFilas,numColumnas)
%Ejemplo: Matriz 4x3 con todos sus elementos unos
>>ones(4,3)
Matriz identidad
eye(orden)
% Ejemplo: Matriz identidad 3x3
>>eye(3)
Matriz diagonal
diag(vector)
%Ejemplo: Una matriz diagonal con el vector [2 3 4]
%en la diagonal
>>diag([2 3 4])
Matriz aleatoria
rand(m,n) randi([imin imax],m,n)
%Ejemplo: Matriz 2x3 de valores aleatorios
>>rand(2,3)
%Ejemplo: Matriz 2x3 con valores aleatorios entre -5 y5
>>randi([-5 5],2,3)
A = [1 2 3; 4 5 6; 7 8 9];
% Accede al elemento en la fila 2, columna 3
elemento = A(2, 3);
% Resultado: elemento = 6
A = [1 2 3; 4 5 6; 7 8 9]; fila2 = A(2, :);
% Accede a todos los elementos de la segunda fila
% Resultado: fila2 = [4 5 6]
A = [1 2 3; 4 5 6; 7 8 9]; columna3 = A(:,3);
% Accede a todos los elementos de
%la tercera columna
% Resultado: columna3 = [3;6;9]
A = [1 2 3; 4 5 6; 7 8 9]; % Matriz 3x3
ultima_fila = A(end, :)
ultimas_columnas=A(:,2:end)
A = [1 2 3; 4 5 6; 7 8 9];
% Submatriz con filas 1 y 2, y columnas 2 y 3
submatriz = A(1:2,2:3);% Resultado: [2 3;5 6]
A = [1 2 3; 4 5 6; 7 8 9];
elementos_mayores_a_5 = A(A>5);
% Resultado: elementos_mayores_a_5 = [6 7 8 9]
Matlab/Octave está diseñado para trabajar de manera óptima con matrices, permitiendo realizar operaciones como la trasposición, productos matriciales y otras manipulaciones comunes.
A = [1 2; 3 4];B = [5 6; 7 8];
C = A+B; % Suma de las matrices A y B
D = A*B; % Producto de las matrices A y B
X = A\B; % X es la matriz que cumple A*X=B
X = A/B; % X es la matriz que cumple X*A=B
X = A^2; % X es A*A
A = [1 2 3; 3 4 5];B = [6 7 8; 9 10 11];
C = A.*B; % Multiplicación elemento a elemento
D = A./B; % División elemento a elemento
D = A.^3; % Potencia elemento a elemento
A = [1 2 3; 3 4 5]; % A es 2x3
A' % Matriz traspuesta de A de orden 3x2
A continuación, se practicará la creación de vectores y matrices y el acceso a sus elementos en varios ejemplos.
p = [3 -2 5 0 1];
% Representa 3x^4 - 2x^3 + 5x^2 + 0x + 1
Para evaluar un polinomio en un punto se utiliza el comando polyval. Para multiplicar, el comando conv y para dividir deconv.
x = 2; p1=[3 -2 5 0 1];p2=[2 3];
valor = polyval(p1, x); disp(valor) % Evalúa p(2)
pmul = conv(p1, p2);
[cociente, resto] = deconv(p1, p2);
Los programas Matlab/Octave ofrecen una amplia variedad de funciones integradas para trabajar con números, vectores, matrices, gráficos y procesamiento de datos. A continuación se muestran algunas de las más comunes, organizadas en categorías.
v = [3 4 -1]; w=[3 4 5] % Vector fila
abs(v); % Valor absoluto de cada elemento
sqrt(w); % Raíz cuadrada de cada elemento
exp(v); % Exponencial de cada elemento
log(w); % Exponencial de cada elemento
round(w); % Redondeo al entero más cercano
floor(w); % Redondeo hacia abajo
round(w); % Redondeo hacía arriba
mod(11,4) % Residuo de la división 11 entre 4
v = [3 4 -1]; % Vector fila
% Seno, coseno, tangente de cada elemento
sin(v), cos(v), tan(v)
% Arcoseno, arcocoseno, y arcotangente
asin(v), acos(v), atan(v)
% Seno, coseno, tangente hiperbólicas
asinh(v), acosh(v), atanh(v)
% Arcoseno, arcocoseno, y arcotangente
% hiperbólicas
asinh(v), acosh(v), atanh(v)
A = [1 7 3;4 8 6]; % Matriz 2x3
size(A) % Tamaño de A
length(A) % Longitud de A, mayor dimensión
trace(A) % Traza de A
sum(A) % Suma de los elementos de A
prod(A) % Producto de los elementos de A
mean(A) % Promedio de los elementos de A
max(A) % Máximo de los elementos de A
min(A) % Mínimo de los elementos de A
sort(A) % Ordena elementos de A
size(A) % Devuelve un vector con el número
% de columnas y filas de la matriz A
A = [1 2; 3 4]; % Matriz 2x2
det(A) % Determinante de A
inv(A) % Inversa de A
eig(A) % Autovalores de A
rank(A) % Rango de A
Una de las características más útiles de Matlab/Octave es su capacidad para crear gráficos de forma
rápida y sencilla. Uno de los comandos a utilizar es plot.
plot(vectorx,vectory,opciones_gráfica)
% Ejemplo: Representar x^2 en [-10,10]
>> x = -10:0.1:10; % Vector de valores x
>> y = x.^2; % Cuadrado de cada valor de x
>> plot(x, y); % Crear la gráfica
En Matlab/Octave, puedes personalizar las gráficas usando opciones como color de línea (por ejemplo, 'r' para rojo), estilo de línea (como '--' para una línea discontinua), y símbolos para representar los puntos (por ejemplo, 'o' para círculos). También puedes combinar estas opciones, por ejemplo, 'b--o' para una línea azul discontinua con círculos.
Otros comandos gráficos:
figure.xlabel,
ylabel.
hold on,
hold off.
grid on,
grid off.
title.subplot(m,n,p) divide la
ventana de gráficos en una cuadrícula de mxn gráficas y selecciona la subgráfica p.
% Datos de ejemplo de temperaturas a lo largo del día
horas = 0:1:23; % Horas de 0 a 23
temp_ciudad1 = [15, 14, 13, 13, 12, 12, 13, 15, 18, 22, 25, 27, 29, 30, 28, 26, 24, 22, 20, 18,
17, 16, 15, 14];
temp_ciudad2 = [10, 9, 9, 8, 8, 7, 8, 10, 13, 18, 20, 23, 25, 26, 24, 23, 21, 19, 17, 15, 13,
12, 11, 10];
% Gráfico de temperatura para la Ciudad 1
% Gráfico en azul
plot(horas, temp_ciudad1, 'b', 'LineWidth', 1.5);
hold on; % Mantiene la gráfica para añadir la segunda
% Gráfico de temperatura para la Ciudad 2
% Gráfico en rojo con línea discontinua
plot(horas, temp_ciudad2, 'r--', 'LineWidth', 1.5);
% Etiquetas y leyenda
xlabel('Hora del día');
ylabel('Temperatura (°C)');
title('Temperatura promedio durante el día en dos ciudades');
legend('Ciudad 1', 'Ciudad 2');
% Mostrar la cuadrícula para facilitar la lectura
grid on;
% Desactivar hold para futuras gráficas
hold off;
Matlab y Octave van más allá de simples calculadoras, incorporan un lenguaje propio de programación con el que se puede crear scripts y funciones, automatizar procesos, manejar bucles y condicionales entre otras posibilidades. A continuación, se presentan los fundamentos básicos del lenguaje de programación.
Funciones
Las funciones en Matlab/Octave permiten encapsular un conjunto de
operaciones dentro de un bloque de código que puede ser reutilizado. Se definen en un archivo
separado, también con la extensión .m. y con el mismo nombre que la
función. En el siguiente ejemplo se muestra la función cuadrado que
calcula, a partir de un valor de entrada, su cuadrado.
function resultado = cuadrado(x)
resultado = x^2;
end
El fichero que tiene esta función deberá llamarse cuadrado.m. La
función se invoca de la misma forma que las funciones predefinidas propias de Matlab/Octave desde la ventana de comandos o desde otro script.
a=cuadrado(2)+1
% Resultado: a=5;.
Para que Matlab pueda utilizar un script o función que hayas creado, el archivo debe guardarse en el directorio de trabajo. Este es el lugar donde Matlab busca por defecto los archivos cuando ejecutas comandos. Puedes ver o cambiar el directorio de trabajo en la barra superior del entorno de Matlab, o usar el comando cd desde la ventana de comandos.
Condicionales
Matlab/Octave admite la estructura de control condicional if-else, que se usa para
ejecutar bloques de código en función de si se cumple o no una condición booleana.

En el ejemplo siguiente, si el valor de x es positivo se escribe el texto "x es positivo", en caso contrario, cuando es menor que cero, se escribe por pantalla "x es negativo" y, en otro caso, se escribe "x es cero".
if x > 0
disp('x es positivo');
elseif x <0
disp('x es negativo');
else
disp('x es cero');
end
Bucles
Matlab/Octave ofrecen dos tipos de estructuras de control para iterar: el bucle for y el bucle while, ambos permiten ejecutar un bloque de código repetidamente bajo distintas condiciones.
La instrucción break fuerza la salida del bucle, de modo que cualquier código restante dentro de esa iteración y las siguientes no se ejecutará. Por su parte, continue interrumpe únicamente la iteración actual.
for. Repite un conjunto de instrucciones cuando varía el
índice en un conjunto de valores.
Con el siguiente código se imprime por pantalla el valor de i cuando va tomando los valores 1, 2, 3, ... ,10.
for i = 1:10
disp(i);
end
Se muestra cómo sumar los cuadrados de los primeros 20 números naturales.
suma = 0; % Inicialización de la suma
for i=1:20
% Agrega el siguiente número a la suma
suma = suma + i^2;
end
Este cálculo se puede hacer también sin utilizar bucles operando con vectores.
vec=1:20;
sum(vec.^2)
while. Repite un conjunto de instrucciones mientras una
condición es verdadera.
Como ejemplo, se verá cómo sumar los primeros números naturales hasta que la suma sea mayor o igual a 300.
suma = 0; % Inicialización de la suma
n = 1; % Número
while suma < 300.
% Agrega el siguiente número a la suma
suma = suma + n;
% Incrementa el contador
n = n + 1;
end
Se muestra ahora cómo se calcula la suma de los números pares desde 2 hasta 10 utilizando un ciclo while.
n = 2; % Número inicial
suma = 0; % Variable para almacenar la suma
% Bucle while
while n <= 10
%Sumar el valor de n a la variable suma
suma = suma +n;
n = n + 2; % Incrementar n en 2
end
suma % Mostrar el resultado: 30
Este cálculo se puede hacer también incluyendo los números en un vector y, a continuación, aplicar la función sum, que devuelve la suma de sus elementos.
sum(2:2:10)
Se incluyen algunos comandos para la lectura y manejo de datos almacenados en ficheros.
fopen,
fscanf.
% Lee todos los números de archivo.txt
fileID = fopen('datos.txt', 'r');
data = fscanf(fileID, '%f');
fclose(fileID);
disp(data);
fprintf.
% Guarda el vector en un archivo de texto
data = [1.1, 2.2, 3.3];
fileID = fopen('output.txt', 'w');
fprintf(fileID, '%f\n', data);
fclose(fileID);
save, load.
% Guarda las variables a y b en archivo.mat
a = 5;
b = [1, 2, 3];
save('variables.mat', 'a', 'b');
load('variables.mat');
A continuación, se presenta un breve cuestionario de Matlab/Octave para consolidar los conceptos clave de este capítulo.
Con el siguiente interactivo puedes realizar una autoevaluación por niveles.
Multiplo que, dados dos números \( k \) y \( h
\), devuelva:
ContarPares que reciba un vector como argumento y
devuelva el número de componentes pares y un vector con dichas componentes.
SumaCifras(325) debería devolver 10.
MCD(24, 15) debería devolver 3. Nota: El MCD(a,b) con a>b es b si a es múltiplo de b. En otro caso, MCD(a,b)=MCD(b,r) siendo r el resto de dividir a entre b.
SumaCuadrados(5, 3, 4) debería
devolver 41.
SuperaMedia que reciba un vector y devuelva otro
vector con los elementos que sean mayores o iguales a la media del vector de entrada.
Algunos aspectos tratados en este capítulo son:

Este tema tiene como objetivo mostrar la importancia de la aritmética computacional en el uso de métodos numéricos. Se analizará cómo los ordenadores representan los números y realizan operaciones, y se evidenciará que, debido a las limitaciones inherentes del sistema, como son el uso del sistema binario y la precisión finita, los resultados obtenidos no siempre son exactos y pueden presentar errores.
En particular, se verá que:
A continuación, se mostrarán ejemplos numéricos que ayudan a entender mejor estos problemas y los errores que pueden aparecer al hacer cálculos en el ordenador. Para más información, se puede consultar
suma=0;n=1000;
for k=1:n
suma=suma+0.1;
end
format longEng;suma
El resultado debería ser $100$ pero se obtiene un número próximo: $99.9999999999986e+000$
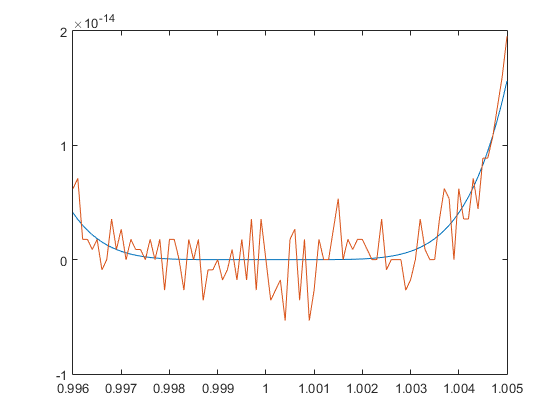
f=@(x) (1-x).^6
%Polinomio expandida la potencia
%syms x ;expand((1-x).^6)
g=@(x) x.^6-6*x.^5+15* x.^4-20*x.^3+15*x.^2-6*x+1
x1=0.996:0.0001:1.005; format longEng;
%Comparamos resultados
[x1' f(x1)' g(x1)']
plot(x1,f(x1),x1,g(x1))
En la figura 2.1 se muestra la gráfica de la función $f(x)$ y la de la función $g(x)$ tras ejecutar el código anterior.
¿Por qué ocurre esto? La razón es que los ordenadores usan un formato (punto flotante binario) que no permite representar de forma precisa números como por ejemplo 0.1, 0.2 o 0.3. Como en general, los números están representados de manera inexacta, las operaciones aritméticas que se realicen también serán inexactas.
Para comprender y aplicar los métodos numéricos, es necesario conocer los sistemas numéricos, ya que constituyen la base para la representación y el tratamiento de los datos en los cálculos.
Un sistema de numeración consiste en un conjunto de símbolos que permiten representar cantidades numéricas, así como reglas para realizar operaciones con dichas cantidades. En este apartado, se verá el sistema decimal (base 10) y el binario (base 2), fundamentales en el ámbito del cálculo numérico. Mientras que el sistema decimal es el que se utiliza en la vida cotidiana, el binario es esencial en computación y en el procesamiento numérico, ya que los ordenadores representan y manipulan los datos a través de este sistema.
En el sistema decimal los números se representan utilizando 10 dígitos: 0,1,2,3,4,5,6,7,8,9. Además, este sistema de numeración es posicional, las cantidades se representan utilizando como base aritmética las potencias del número diez. Así, si $x \in \mathbb{R}^{+}$, se puede escribir
$$x = \sum\limits_{ - \infty }^n {{a_k} \cdot {{10}^k}} \,\,\,\,\, 0 \le {a_k} \le 9$$Si se considera una base $b$, un número real $x$ positivo se puede escribir de la forma
$$x = \sum\limits_{ - \infty }^n {{a_k} \cdot {b^k}} \,\,\,\,\, 0 \le {a_k} \le b - 1$$ o también $$x = {a_n}{a_{n - 1}}...{a_0}.{a_{ - 1}}{a_{ - 2}}{a_{ - 3}}...$$El Standard de IEEE (Institute of Electrical and Electronics Engineers) propone el uso de la base $b=2$ en el almacenamiento y la aritmética sobre el computador. En este sistema de numeración los números se representan utilizando solamente las cifras cero y uno (0 y 1). Así, si $x$ es positivo,
$$x = \sum\limits_{ - \infty }^n {{a_k} \cdot {2^k}} \,\,\,\,\, {a_k} \in \{ 0,1 \}$$Para convertir un número decimal entero a binario, basta dividir el número y sus cocientes entre 2, acumulando los restos o residuos de la division. La lista de ceros y unos leídos de abajo a arriba, darán la expresión en binario. Se describe este proceso a continuación.
El proceso se repite con $x_1$ y el resto de cocientes hasta que el cociente sea menor que 2
$$x=2\cdot {\color {red} (2\cdot x_2+r_2)}+{\color {blue} r_1} =2^2 {\color {red} x_2}+2{\color {blue} r_2}+ {\color {blue} r_1} ... $$ Los números $ {\color {blue} r_1}$, $ {\color {blue} r_2}$... nos darán las cifras de la expresión binaria de $x$.
Se tiene que,
$$ \begin{aligned}{1 \over {10}} &= {1 \over {{2^4}}} + {1 \over {{2^5}}} + {0 \over {{2^6}}} +
{0 \over {{2^7}}} + {1 \over {{2^8}}} + {1 \over {{2^9}}} + {0 \over {{2^6}}} + {0 \over
{{2^7}}} + ... \\ &= 0.0001{\widehat {1001}_2} \end{aligned}$$
Para convertir un número binario a decimal, basta multiplicar cada dígito binario por la potencia de 2 correspondiente a su posición y luego se suman todos los valores resultantes.
Se muestra en el siguiente ejemplo cómo se convierte a decimal un número binario con parte fraccionaria.
Se tiene que: $$\begin{aligned} x = 1·2^1 + 0·2^0 + 1·2^{-1}+ 1·2^{-2} + \\ +1·2^{-3}+ 0·2^{-4} + 0·2^{-5} + 1·2^{-6} \\ = 1+1/2+1/4+1/8+1/64=1.890625\end{aligned}$$
Un número real $x$ en base 10 se puede escribir de forma que la primera cifra no nula aparecezca inmediatamente a la izquierda del punto decimal, es decir, de la forma
$$x = {\left( { - 1} \right)^s}× \,{10^e} × \,a.m$$donde
Esta expresión se dice que está
Como los ordenadores utilizan aritmética binaria, en base 2, cualquier número $x$ se puede escribir normalizado de la forma
$$x = {\left( { - 1} \right)^s} × \,{2^e} × \,1.m$$
Así, el número $x$ se puede almacenar guardando el signo $s$, el exponente $e$ y la mantisa $m$. Como en base 2 el primer dígito que precede a la mantisa es siempre 1, no es necesario almacenarlo. De esta forma se optimiza la representación mediante el llamado
Los números reales se representan en el ordenador según la norma IEEE 754, establecida en 1985
por el Institute of Electrical and Electronics Engineers (IEEE). Esta norma establece dos formatos a partir de la expresión
normalizada en coma flotante:
Para representar un número real en precisión simple en el ordenador se utiliza:
Teniendo en cuenta que se usan 8 bits para el exponente, sus valores posibles variarían desde 0 hasta 255:
$$\underbrace {00000000}_{8\, bits}\,\,\,\,\,\,\,\,\text{hasta}\,\,\,\,\,\,\underbrace {11111111}_{8 \,bits} \equiv 1 + 2 + ... + {2^{7}} = {2^{8}} - 1 = 255$$Con objeto de poder considerar las potencias de 2 negativas se hace un desplazamiento del exponente para que represente valores desde -127 a 128. Así, en precisión simple, un exponente real de 0 se almacena
como 127, un exponente de -1 como 126, y un exponente de +1 como 128.
En general, la relación entre el exponente real y el almacenado es la siguiente:
$$e_{almacenado}=e_{real}+127$$
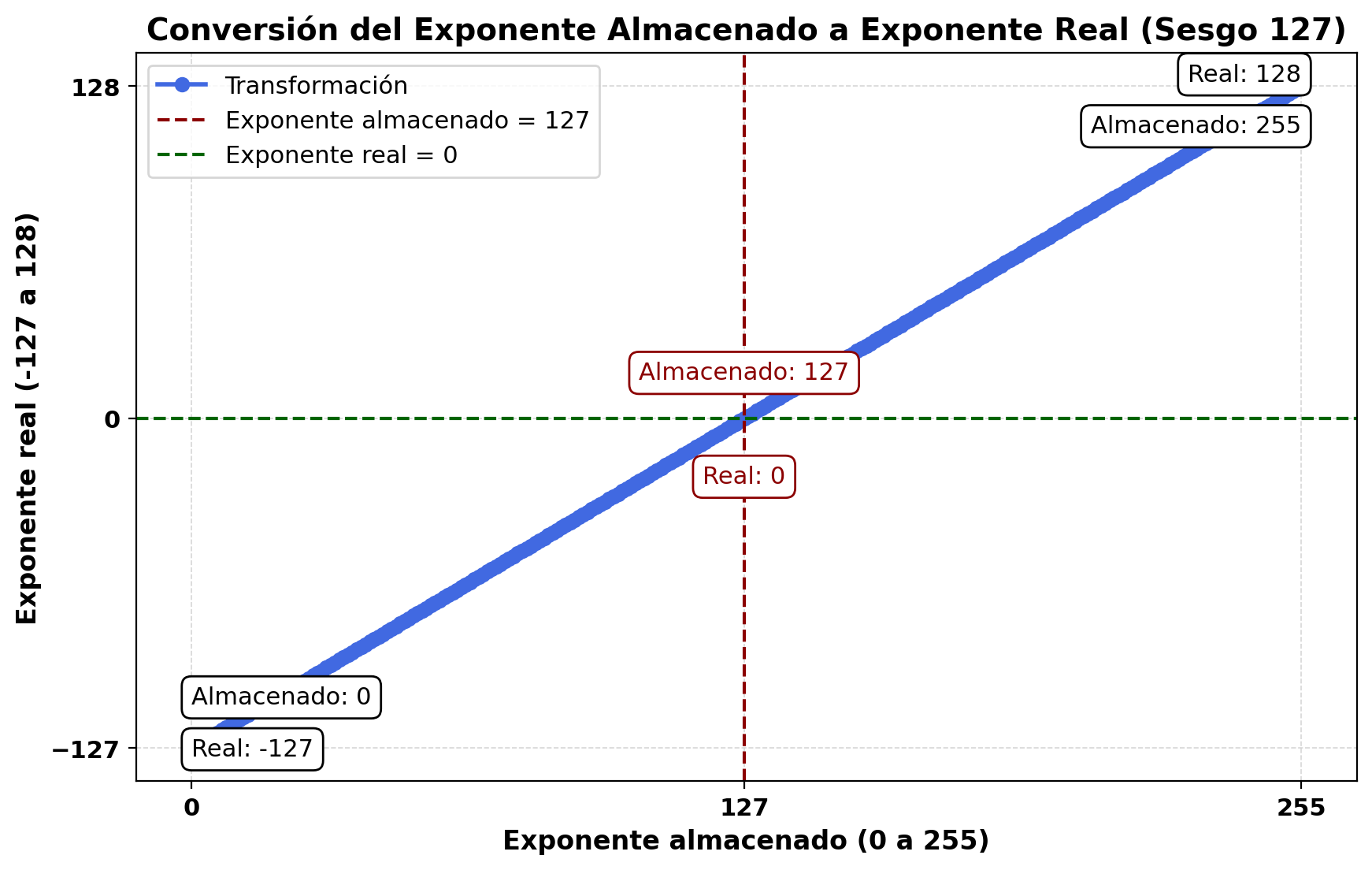
Los valores extremos del exponente, esto es 0 y 255, se reservan para números especiales (cero e infinito).
Se tiene que
$$3.125_{10}=11.001_{2}=1.1001 × 2^{1}$$Por lo tanto, $m=1001$ que ajustada a 23 bits es $1001\underbrace{0...0}_{19 \,\,bits}$.
Para el exponente, considerando el sesgo, se codificará $e=127+1=128=2^{7}$. Este número en binario es $10000000$.
En definitiva, la representacion en precisión simple del número decimal 3.125 es la siguiente:
$$0 10000000 1001\underbrace{0...0}_{19 \,\,bits}$$
En Matlab la precisión que se usará para los cálculos será
Teniendo en cuenta que el exponente se almacena en 11 bits, los valores que se pueden considerar para el exponente son desde 0 hasta 2047:
$$\underbrace {0....0}_{11 \,bits}\,\,\,\,\,\,\,\,\text{hasta}\,\,\,\,\,\,\underbrace {1....1}_{11 \,bits} \equiv 1 + 2 + ... + {2^{10}} = {2^{11}} - 1 = 2047$$
Para poder considerar las potencias de 2 negativas se toma un desplazamiento o
Se consideran las siguientes representaciones especiales:
Respecto al exponente, el valor a almacenar es $e=1023+1=1024=2^{10}$, que en binario es $10000000000$.
El número se almacenará de la forma:
$$ \underbrace{0}_{signo} \underbrace{10000000000}_{exponente}\,\,\underbrace{10010...0}_{mantisa, \,48\,\,últimos \,\,bits\,\,0}$$Dado que la representación de números reales bajo estos formatos es aproximada, hay dos conceptos importantes en la aritmética en punto flotante.
realmax en Matlab
realmin en Matlab
Si se considera que el bit escondido es cero, se pueden obtener números menores que el mínimo número normalizado mediante la siguiente representación: $$x = \left( { - 1} \right)^s × 2^{- 1022} × \,\,0.f$$
Estos números se dicen que están
El mínimo número desnormalizado positivo ocurre cuando la mantisa tiene un 1 en el bit menos significativo $m=2^{-52}$. El exponente real será
$$ {2^{ - 1022}} \cdot {2^{ - 52}} = {2^{ - 1074}}$$Todos los números menores que este valor se consideran 0.
>>2^(-1074)
ans=
4.9407e-324
>>2^(-1075}
ans=
0
El número más pequeño representable después del 1 utilizando representación binaria en punto flotante con doble precisión es:
$$1 = \left( { + 1} \right)× {{\rm{2}}^0}× 1.\underbrace {00...0}_{52}$$ $$1 + \varepsilon = \left( { + 1} \right)× {{\rm{2}}^0}× 1.\underbrace {00...01}_{52}$$
El valor de $\epsilon$ se llama eps: $\varepsilon_m = {2^{ - 52}}$.
El número más pequeño $\varepsilon$ de forma que $1-\varepsilon \ne 1$ es ${2^{ - 53}}$. Por tanto, las distancias entre el número que antecede a 1 y el que le precede son respectivamente $\varepsilon_m/2$ y $\varepsilon_m$.
eps(x).
Para cuantificar el error, se introducen los conceptos de error absoluto y error relativo. Si $\widetilde p$ es una aproximación de $p$, se define:
El error absoluto indica la desviación de una medición respecto al valor real, expresada en las mismas unidades. El error relativo, en cambio, representa esa desviación como una fracción del valor real; si se multiplica por 100, se obtiene el error porcentual, lo que permite comparar errores en magnitudes de distinta escala.
En general, en los métodos numéricos no se conoce el valor verdadero, por lo tanto tampoco se conocerá el error real. Lo frecuente es tener una estimación del error a partir de una cota positiva del error máximo.
En este ejemplo se muestra que si bien el error absoluto es distinto, el error relativo es el mismo. El error relativo de 3% indica que la medición tiene un error de aproximadamente el 3% respecto al valor real.
En la tabla siguiente se recogen los errores absoluto y relativo para cada estimación.
| Medición | Valor estimado | Valor real | Error absoluto | Error relativo |
|---|---|---|---|---|
| Velocidad de la luz (Foucault) | 298 000 | 299 776 | 1 776 | 5.920661e-03 |
| Constante de Planck | 6.41e-27 | 6.626e-27 | 2.13e-28 | 3.216246e-02 |
Para determinar cuál es la medición más precisa, se analiza el error relativo:
En el sistema decimal, existen distintas formas de redondear un número a $t$ decimales. En el proceso
denominado
El número 3.246 se representaría como 3.24 si se usa truncamiento o bien 3.25 si se usa redondeo. El truncamiento elimina todas las cifras que no pueden ser representadas por la máquina, en este caso a partir del tercer decimal. El redondeo, toma la primera cifra no representable, en este ejemplo, sería el 6 y le suma una unidad al último dígito si es mayor o igual a 5 o lo trunca si es menor que 5.
Se considera el número
$$x = {\left( { - 1} \right)^s}× {2^{{e_x}}} × 1.f\,\,\,\,\,\,\,\,\,\,\,\,\,\,-1023 < {e_x} < 1024$$
y se denota por
Por lo tanto, el épsilon de la máquina es una cota superior del error de redondeo en el sistema punto flotante.
Si $\otimes$ es una operáción aritmética como una suma, resta, multiplicación o división, el cálculo sigue el siguiente proceso:
La representación de la operación es entonces
$$fl\left( {x \otimes y} \right) = fl\left( {fl\left( x \right) \otimes fl\left( y \right)} \right)$$ En consecuencia, el orden en el que se realizan las operaciones puede modificar el resultado final. Con el siguiente ejemplo se muestra que puede no cumplirse la propiedad asociativa.
x=10^20;y=-10^20;z=1;
x+(y+z)
(x+y)+z
x=1- 3*(4/3 - 1)
x =
2.2204e-16
El valor exacto es $112.7$. El calculo sería de la siguiente manera
$$fl(1025)=1.02 \cdot 10^3 \,\,\,\,\,\,fl(912.3)=9.12\cdot 10^2$$ $$fl(1025-912.3)=fl(112.7)=1.12 \cdot 10^2$$ $$ fl(fl(x)-fl(y))=fl(108)=1.08 \cdot 10^2$$Además, cuando se realiza una cadena de operaciones, los errores de redondeo pueden acumularse de modo que resten validez al resultado. Para controlar la propagación de errores de redondeo, es necesario buscar algoritmos con el número mínimo de operaciones convenientemente dispuestas para evitar estos problemas y que a la vez el tiempo de ejecucion sea aceptable.
Para un análisis detallado sobre los errores en cálculos numéricos, como son los errores de redondeo,
truncamiento y su propagación, se recomienda consultar los libros
Este error se produce cuando se calcula la diferencia de dos números bastante próximos y el redondeo del ordenador iguala esa diferencia a cero.
% Primer ejemplo
x=1+2^-54;y=1;x-y
% Segundo ejemplo
x=2^60+2^6;y=2^60;x-y
f=@(x) (exp(x)-1).^2+(1./sqrt(1+x.^2)-1).^2; k=-1:-1:-17;h=10.^(k);
v=(f(1+h)-f(1))./h;
format longEng
disp([h' v'])
Si se considera el cálculo tomando el inverso de $e^{40}$, se evita este problema de cancelación ya que todos los términos son positivos. El cálculo con Matlab/Octave se muestra a continuación.
x=40; %Inverso del número a calcular e^-40=1/e^40
suma=1;p=1;
for k=1:99
p=p*(x/k);
suma=suma+p;
end
1/suma
x=-40; %Sin considerar el inverso
suma=1;p=1;
for k=1:99
p=p*(x/k);
suma=suma+p;
end
suma
%Valor que da Matlab
exp(-40) % 4.248354255291589e-018
En los siguientes ejemplos, se muestra como una reformulación del cálculo evita el problema de cancilación en algunas situaciones.
Se escribe el código Matlab/Octave para realizar los cálculos.
%Se considera la primera expresión como resta de fracciones
f=@(x) 1./(1+2*x)-(1-x)./(1+x);
%Se realiza la suma para evitar la cancelación
g=@(x) 2*x.^2./((1+2*x).*(1+x));
format longEng
%Se considera un vector de valores próximos a cero
k=-1:-1:-17;
h=10.^k;
%Se evalúan ambas expresiones
f1=f(h);
g1=g(h);
%Se imprimen los valores de h y los valores
%obtenidos para comparar
disp([h' f1' g1'])
La expresión equivalente es $f(x)=\frac{1-cos^2(x)} {x (1+cos/x)}=\frac{sen^2(x)} {x (1+cos/x)}$.
f=@(x) (1-cos(x))./x;
%Se multiplica y divide por (1+cos(x))
g=@(x) sin(x).^2./(x.*(1+cos(x)));
k=-1:-1:-17;h=10.^k;f1=f(h);g1=g(h);
format longEng
disp([h' f1' g1'])
Multiplicando y dividiendo por el conjungado del numerador
$$f\left( x \right) = \frac{{\sqrt {{x^2} + 1} - \sqrt {{x^2} - x} }}{{x\,}} = \frac{2}{{x\,\left( {\sqrt {{x^2} + 1} + \sqrt {{x^2} - x} } \right)}}$$
f=@(x) sqrt(x+1./x)-sqrt(x-1./x);
%Se multiplica y divide por el conjugado
g=@(x) 2./(x.*(sqrt(x.^2+1)+sqrt(x.^2-x)));
k=1:25;h=10.^k;f1=f(h);g1=g(h);
format longEng
disp([h' f1' g1'])
Con frecuencia, una operación aritmética con dos números válidos da como resultado un número tan
grande o tan pequeño que el ordenador no puede manejarlo; como consecuencia, se produce un
realmax para ilustrar el concepto de
desbordamiento. Divide después por 2 el valor mínimo positivo normalizado, realmin y observa que se
representa por cero.
Se realizan los cálculos con Matlab/Octave.
% Valor máximo representable
maxVal = realmax;
% Se intenta exceder el valor máximo
num = maxVal * 2;
disp(['Desbordamiento resulta en: ', num2str(num)]);
% Valor mínimo positivo normalizado representable
minVal = realmin;
% Se intenta obtener un valor menor al mínimo
num = minVal * 1e-100;
disp(['Subdesbordamiento resulta en: ', num2str(num)]);
En el siguiente ejemplo se verá que si el algoritmo no es adecuado, los errores de redondeo pueden conducir a resultados incorrectos. Este fenómeno, conocido como inestabilidad numérica, puede evitarse seleccionando algoritmos más apropiados.
Realizando el cálculo directo $I_{30}$ e $I_{31}$ de forma iterativa con Matlab/Octave se obtienen valores negativos. El valor de $I_{30}$ que se otiene es -0.357484694711417 y para el valor de $I_{31}$ se obtiene -2.312387998625434
a=2/pi; v(1)=1/pi;v(2)=1/pi-2*a/pi^2;
format longEng
for k=3:31;
v(k)=1/pi-k*(k-1)*v(k-2)/pi^2;
end
disp([[1:31]' v'])
Esto es imposible porque el integrando es positivo y por tanto las integrales deben ser positivas.
Se verá cómo obtener los valores de estas integrales de otra forma. Despejando $I_n$ en función de $I_{n+2}$ se tiene:
\[\frac{{\left( {n + 2} \right)\left( {n + 1} \right)}}{\pi }{I_n} = 1 - \pi {I_{n + 2}}\] \[{I_n} = \frac{\pi }{{\left( {n + 2} \right)\left( {n + 1} \right)}}\left( {1 - \pi {I_{n + 2}}} \right)\] \[{I_n} = \frac{{{\pi ^2}}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\left( {\frac{1}{\pi } - {I_{n + 2}}} \right)\]Si se toman límites cuando $n$ tiene a infinito, se puede ver que la sucesión $I_n$ tiende a cero. Basta tener en cuenta que
$$\left| {\int\limits_0^1 {{x^n}sen\left( {\pi x} \right)dx\,} } \right| \le \int\limits_0^1 {{x^n}dx\,} = \left. {{{{x^{n + 1}}} \over {n + 1}}} \right|_{x = 0}^{x=1} = {1 \over {n + 1}}$$Por ello, para utilizar esta expresión hacia atrás, se debe partir de dos valores $I_{n+2}$ e $I_{n+1}$ próximos a cero para un valor de $n$ alto. En el siguiente código se ha considerado $I_{56}$ e $I_{55}$ como 0.
a=56;
w(56)=0;w(55)=0;
for k=a-2:-1:1;
w(k)=pi^2/((k+2)*(k+1))*(1/pi-w(k+2));
end
disp([[1:56]' w'])
El valor de $I_{30}$, utilizando este cálculo, es $0.003139287076703$, y el valor de $I_{31}$ es $0.002950500704051$.
Se pide calcular de forma recurrente el valor de $y_{20}$ con la expresión obtenida: $y_n=\frac{1}{n} - 5{y_{n - 1}}$. Considera después la fórmula de recurrencia en sentido descendente para obtener el valor de $y_{20}$ resultado de despejar $y_{n-1}$ en función de $y_n$:
\[{y_{n - 1}} = \frac{1}{{5n}} - \frac{{{y_n}}}{5}\] Justifica los resultados obtenidos.En el cálculo recurrente de ${y_n} = \frac{1}{n} - 5{y_{n - 1}}$ se puede observar que se obtiene un valor negativo, lo cual es absurdo porque el integrando es positivo. Este error se produce porque se restan dos números del mismo signo de magnitud similar.
El código para obtener $y_{20}$ con esta ley de recurrencia es:
clear all
y(1)=1-5*(log(6)-log(5));
format longEng
for k=2:20;
y(k)=1/k-5*y(k-1);
end
disp([[1:20]' y'])
Tomando límites en ${y_n} = \frac{1}{n} - 5{y_{n - 1}}$ cuando $n$ tiende a $\infty$, se ve que la sucesión $y_n$ converge a 0. Por lo tanto, considerando por ejemplo $y_{60}=0$, se calcula de nuevo el valor de $y_{20}$ utilizando la ley de recurrencia descendente ${y_{n - 1}} = \frac{1}{{5n}} - \frac{{{y_n}}}{5}$.
y(60)=0;
format longEng
for k=60:-1:2;
y(k-1)=1/(5*k)-y(k)/5;
end
disp([(1:60)' y'])
%y(20) es 7.997523028232164e-03
Además, se ha analizado los errores de redondeo y truncamiento, destacando la importancia de desarrollar algoritmos numéricos que minimicen estos problemas en aplicaciones prácticas.
Los aspectos clave analizados en este tema son:
Entender estas limitaciones es esencial para abordar problemas numéricos con precisión.

El propósito de los métodos numéricos para resolver ecuaciones no lineales es encontrar raíces aproximadas, ya que la mayoría de
las ecuaciones no tienen soluciones exactas o estas no son computacionalmente viables. Mediante
métodos iterativos se va consiguiendo aproximar la solución dentro de un margen de error considerado
Entre las aplicaciones más importantes de los métodos numéricos está la resolución de ecuaciones no lineales, una tarea esencial en disciplinas como física, ingeniería, economía y muchas otras áreas de la ciencia. Estas ecuaciones, donde la variable aparece de forma no lineal son clave para modelar fenómenos reales, desde el diseño de estructuras hasta la dinámica de sistemas físicos. Sin embargo, muchas veces estas ecuaciones no tienen soluciones exactas en términos algebraicos, por lo que se buscan soluciones aproximadas.
Se considera por ejemplo la siguiente ecuación obtenida a partir de la segunda ley de Newton para calcular la velocidad de un paracaidista,
$$v = {{g \cdot m} \over c}\left( {1 - {e^{ - {c \over m}t}}} \right)$$donde la velocidad $v$ depende de la variable independiente tiempo, $t$, $g$ es la constante de gravitación, $c$ el coeficiente de resistencia y $m$ es la masa del paracaidista.
Si se quisiera obtener el coeficiente de resistencia del paracaidista con una masa dada, ¿cómo se obtendría este valor para alcanzar una velocidad determinada en un periodo establecido? La respuesta se obtendría calculando $c$ que hace cero a la siguiente función
$$f\left( c \right) = {{g \cdot m} \over c}\left( {1 - {e^{ - {c \over m}t}}} \right) - v$$esto es, habría que calcular el valor de $c$ tal que $f(c)=0$.
Cuando ocurre como en este caso, y no es posible encontrar analíticamente el cero de la función o pudiendo encontrarlo su cálculo es complicado, se utilizan algoritmos que determinan, en un número finito de pasos, un valor aproximado de la raíz buscada. Estos métodos de aproximación generalmente son iterativos y conducen a una solución a través de una sucesión $x_0, x_1, ..., x_k,...$ que converge al valor $\alpha$ que cumple $f(\alpha)=0$.
A lo largo de la historia, la resolución de ecuaciones no lineales ha evolucionado desde métodos manuales hasta complejos algoritmos implementados en ordenadores modernos. En la antigüedad, los babilonios y griegos ya aplicaban principios numéricos para resolver problemas matemáticos. Así, el método de bisección, que tiene sus orígenes en la antigüedad, utiliza un enfoque simple: dividir un intervalo y localizar la raíz mediante evaluaciones intermedias.
Otros
métodos, como el de Newton-Raphson, desarrollado en el siglo XVII por Isaac Newton
 Isaac
Newton (1642-1727) fue un físico, matemático y astrónomo inglés, considerado uno de los
científicos más influyentes de la historia. Desarrolló las leyes del movimiento y la
gravitación universal, así como importantes contribuciones al cálculo, óptica y mecánica. Su
obra más destacada, Philosophiæ Naturalis Principia Mathematica, sentó las bases de la
física clásica.
y Joseph Raphson
Isaac
Newton (1642-1727) fue un físico, matemático y astrónomo inglés, considerado uno de los
científicos más influyentes de la historia. Desarrolló las leyes del movimiento y la
gravitación universal, así como importantes contribuciones al cálculo, óptica y mecánica. Su
obra más destacada, Philosophiæ Naturalis Principia Mathematica, sentó las bases de la
física clásica.
y Joseph Raphson
 Joseph
Raphson (1648-1715) fue un matemático inglés conocido por su trabajo en análisis numérico.
Publicó el método de Newton-Raphson en su obra Analysis Aequationum Universalis (1690), una
técnica iterativa para encontrar raíces de ecuaciones no lineales. Su versión mejorada del
método de Newton fue más algebraica y general, contribuyendo al desarrollo de la matemática
aplicada., aprovechan herramientas del cálculo diferencial
utilizando la pendiente de las tangentes de la función.
Joseph
Raphson (1648-1715) fue un matemático inglés conocido por su trabajo en análisis numérico.
Publicó el método de Newton-Raphson en su obra Analysis Aequationum Universalis (1690), una
técnica iterativa para encontrar raíces de ecuaciones no lineales. Su versión mejorada del
método de Newton fue más algebraica y general, contribuyendo al desarrollo de la matemática
aplicada., aprovechan herramientas del cálculo diferencial
utilizando la pendiente de las tangentes de la función.
En el siglo XX, con el desarrollo de la computación, matemáticos como Alan Turing
 Alan Turing (1912–1954) fue un matemático británico, considerado uno de los padres de la computación moderna. Desarrolló el concepto de la máquina de Turing, base teórica de los algoritmos, y desempeñó un papel crucial en la Segunda Guerra Mundial al descifrar los códigos nazis de la máquina Enigma. Su trabajo sentó las bases de la inteligencia artificial y la informática teórica..
y John von
Neumann
Alan Turing (1912–1954) fue un matemático británico, considerado uno de los padres de la computación moderna. Desarrolló el concepto de la máquina de Turing, base teórica de los algoritmos, y desempeñó un papel crucial en la Segunda Guerra Mundial al descifrar los códigos nazis de la máquina Enigma. Su trabajo sentó las bases de la inteligencia artificial y la informática teórica..
y John von
Neumann
 John
von Neumann (1903-1957) fue un matemático, físico y pionero de la computación
húngaro-estadounidense. Contribuyó al desarrollo de la teoría de juegos, la mecánica
cuántica y los métodos numéricos en computación científica. Fue clave en la creación de las
primeras computadoras y en la formulación de la arquitectura de Von Neumann, base de los
sistemas computacionales modernos.
sentaron las bases para implementar estos métodos en máquinas, haciendo posible resolver
problemas que antes eran inabordables.
John
von Neumann (1903-1957) fue un matemático, físico y pionero de la computación
húngaro-estadounidense. Contribuyó al desarrollo de la teoría de juegos, la mecánica
cuántica y los métodos numéricos en computación científica. Fue clave en la creación de las
primeras computadoras y en la formulación de la arquitectura de Von Neumann, base de los
sistemas computacionales modernos.
sentaron las bases para implementar estos métodos en máquinas, haciendo posible resolver
problemas que antes eran inabordables.
En el siguiente video se da una visión rápida de los métodos más importantes que se tratan en este capítulo.
Se comenzará con el método de bisección, una técnica basada en el teorema de Bolzano, que garantiza la existencia de raíces en un intervalo y ofrece una convergencia segura aunque lenta. Luego se estudiará el método del punto fijo, que transforma la ecuación en una forma iterativa y permite analizar la convergencia local y global de la solución. Posteriormente, se explorará el método de Newton-Raphson, que emplea la derivada de la función para obtener una convergencia rápida, aunque con ciertas limitaciones respecto a su punto de inicio. Finalmente, se analizará el método de la secante, que evita el cálculo de derivadas.
A la vez que se van mostrando los distintos métodos, se irán presentado ejemplos prácticos para ilustrar el comportamiento de cada uno de ellos, comparando sus ventajas y limitaciones en diferentes situaciones. Para más información, se puede consultar
A cualquier solución de la ecuación $f(x)=0$ se le llama
Se puede demostrar que si $f$ es $C^m(I)$, es decir, es derivable hasta el orden $m$ con derivadas continuas, y $\alpha$ es un punto de $I$, la función tiene un cero de multiplicidad $m$ en $\alpha$ si
$$f(\alpha)=f'(\alpha)=...=f^{(m-1}(\alpha)=0, f^{(m}(\alpha) \ne 0$$En un primer paso para obtener las raíces de una función, se busca un intervalo donde se encuentre uno o varios ceros de la función. Posteriormente, se buscan intervalos que contengan una sola raíz. El siguiente teorema ayuda en esta localización y separación de raíces.
TEOREMA DE BOLZANO: Si $f$ es una función continua en $[a,b]$ de manera que $f(a)f(b) < 0$, entonces existe al menos un cero de la función en el intervalo $(a,b)$.
El hecho de que la función $f$ tenga un cero, no significa que sea único. Si se añaden condiciones adicionales, como por ejemplo la monotonía estricta de $f$ en un intervalo $I$, sí se podría garantizar que la solución de $f(x)=0$ es única en dicho intervalo.
Se recuerda que en el caso de que la función sea derivable, si $f'(x)> 0$ en todo punto de $I$ la función es estrictamente creciente en $I$. Análogamente, si $f'(x)< 0$ en $I$ entonces es estrictamente decreciente.
Si la función es estrictamente creciente o estrictamente decreciente en un intervalo donde hay cambio de signo en los extremos, la función tiene un único cero en dicho intervalo.
Este proceso depende tanto de la función $G$ como del punto inicial $x_0$ y los algoritmos a utilizar deberán dar respuesta a cuestiones sobre su convergencia como son:
Se dice que un algoritmo
Cuando la solución converge hacia la solución únicamente si el punto $x_0$ pertenece a un cierto
entorno, la convergencia se dice que es
No siempre es mejor considerar un algoritmo que converja globalmente, a veces, un algoritmo localmente convergente, puede tener una "velocidad de convergencia" mayor si bien este tipo de algoritmos plantean la dificultad de cómo elegir el intervalo adecuado donde considerar $x_0$.
El método de aproximaciones sucesivas o punto fijo, que consiste en partir de un punto $x_0$ y calcular los demás términos de la sucesión $x_n$ de la forma $x_{n+1}=g(x_n)$ para obtener un punto fijo de $g$, tiene una convergencia más lenta que el método de Newton que converge localmente.
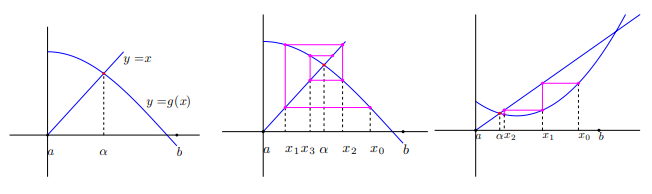
Se distinguen distintas velocidades de convergencia que se pasarán a definir.
Dada una sucesión de números reales, $\left\{ {x _k} \right\}_{k = 1}^\infty $, convergente
hacia un punto $\overline x$, se dice que su
$$\left| {{x_{k + 1}} - \overline x }
\right| \le {C_p}{\left| {{x_k} - \overline x \,} \right|^p}$$ para todo $ k \ge k_0$ siendo
$k_0$ entero.
En particular,
Se tiene que
Se dice que la sucesión $\{x_k\}_{k = 1}^\infty$
Se puede observar que si la sucesión tiene una velocidad de convergencia $p$ mayor que 1 entonces converge superlinealmente. Bastaría tomar $${\varepsilon _k} = {C_p}{\left| {{x_k} - \bar x{\mkern 1mu} } \right|^{p - 1}}\,\,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \forall k \ge 0$$
El siguiente resultado permite determinar un test de parada de las iteraciones cuando la convergencia es superlineal.
Si $\{x_k\}_{k = 1}^\infty$ converge superlinealmente a ${\bar x}$ entonces $$\mathop {\lim }\limits_{k \to \infty } {{\left| {{x_{k + 1}} - {x_k}{\mkern 1mu} } \right|} \over {\left| {{x_k} - \bar x{\mkern 1mu} } \right|}} = 1$$
En este caso, una vez establecida la precisión que se quiere alcanzar,$\varepsilon > 0$, puede considerarse como test de parada:
$$\left| {{x_{k + 1}} - {x_k}} \right| < \varepsilon$$se compara así dos iteraciones consecutivas y se mira la coincidencia de dígitos que se considere (fijado por el valor de $\epsilon$).
El límite de la sucesión se obtiene resolviendo la ecuación
\[{\bar x} = \frac{\bar x}{{1.1}} + 3 \Rightarrow x\left( {1 - \frac{1}{{1.1}}} \right) = 3 \Rightarrow \bar x = 33\] Se analiza en la siguiente tabla cómo los valores de la sucesión están próximos y, sin embargo, están lejos del valor límite.| k | xk | |xk+1 - xk| |
|---|---|---|
| 0 | 100.0000 | - |
| 1 | 93.0909 | 6.9091 |
| .. | .. | .. |
| 7 | 69.5798 | 2.1570 |
| 8 | 68.9844 | 0.5954 |
| 9 | 68.0767 | 0.9077 |
| 10 | 67.7970 | 0.2797 |
| 11 | 67.6337 | 0.1633 |
| 12 | 67.5398 | 0.0939 |
| 13 | 67.4907 | 0.0491 |
| 14 | 67.4633 | 0.0274 |
| 15 | 67.4476 | 0.0157 |
| 16 | 67.4387 | 0.0089 |
| 17 | 67.4330 | 0.0057 |
| 18 | 67.4295 | 0.0035 |
Aplicando el teorema de Bolzano, una forma sencilla de aproximar el cero de una función continua es dividir el intervalo en dos y elegir el subintervalo en el que se sigue produciendo el cambio de signo. Repitiendo este proceso se puede llegar a conseguir una aproximación de la solución de $f(x) = 0$ tan precisa como se desee.
| $f(x)$ | $a$ | $b$ |
|---|---|---|
| $cos(x)-x$ | $0$ | $2$ |
| $sen(x)$ | $-0.5$ | $\pi/3$ |
| $x^2-sen(x)$ | 0.5 | 1.3 |
En primer lugar, se ve que cada función tiene un único cero en el intervalo indicado.
Para calcular los valores de las tres primeras iteraciones del método de la bisección, se puede utilizar la herramienta interactiva siguiente introduciendo la función y los valores de $a$ y $b$ para cada caso. En el interactivo se debe escribir seno de x como sin(x).
Biseccion(a,b,tol,maxiter) que tenga como parámetros los extremos del intervalo a y
b, la tolerancia toly el máximo de iteraciones maxiter para calcular los ceros de la función $f(x)=x^3-6x^2+11x-6$ en el intervalo $[0, 1.5]$
tomando como tolerancia el valor $0.001$ y el valor de $30$ como máximo de iteraciones. Nota: En este polinomio las raíces se pueden calcular de forma exacta, son 1, 2 y 3 por lo que este ejemplo únicamente tiene interés como ejemplo teórico.
La herramienta interactiva siguiente construye el código de la función Biseccion2(a,b,tol,maxiter). Para ello, se debe pulsar en el
botón
Definida esta función en un fichero .m, bastaría calcular los ceros en cada intervalo escribiendo en la ventana de comandos:
Biseccion(0,1.5,10^-3,30) %Solución: 1.0000
Biseccion(1.5,2.5,10^-3,30) %Solución: 2.0000
Biseccion(2.5,3.5,10^-3,30) %Solución: 3.0000
Biseccion(fun,a,b,tol,maxiter).
Calcula con esta función el cero de $f(x)=x^3-6x^2+11x-6$ en el intervalo $[0,1.5]$, con una tolerancia $10^{-6}$ y un máximo de 25 iteraciones.
Suponiendo que en el intervalo $[a,b]$ hay cambio de signo de $f$, la función pedida podría ser la siguiente.
function raiz = Biseccion2(f, a, b, tol, maxIter)
raiz='';
for i = 1:maxIter
c = (a + b) / 2;
fc = f(c); fa = f(a);
if fa * fc < 0
b = c;
else
a = c;
end
if abs(f(c)) < tol
raiz = c;
break;
end
end
end
Para calcular el cero de $f(x)=x^3-6x^2+11x-6$ en el intervalo $[0, 1.5]$, con una tolerancia $10^{-6}$ y un máximo de 25 iteraciones, se deberá escribir el código siguiente.
f=@(x) x.^3-6*x.^2+11*x-6;
%Se comprueba que hay cambio de signo
f(0)*f(1.5)
Biseccion2(f,0,1.5,10^-6,25)
%Solución: 1.0000
En los resultados teóricos que se enuncian a continuación, se dan condiciones suficientes para que haya un punto fijo de una función $g$ en un intervalo y para que la convergencia sea a un único punto fijo.
Si al utilizar el método del punto fijo $x_{k+1}$ y $x_k$ coinciden dentro de la exactitud especificada $\epsilon$, no significa que $\overline x \approx {x_{k+1}}$ con la misma exactitud. En general, esta afirmación no es correcta. Si $g'(x)$ está próxima a la unidad, entonces la cantidad $\left| {{x_k} - \overline x} \right|$ puede ser grande, aún cuando $\left| {{x_{k+1}} - x_k} \right|$ sea extremadamente pequeña.
g=@(x) x-x.^2/10; h=@(x) x;
% Gráfica de la función
fplot(g, [-2, 2]); hold on;
fplot(h, [-2, 2], 'r--'); % Línea y = x
xlabel('x');ylabel('g(x)');
title('Método del Punto Fijo para g(x) = x - x^2/10');
grid on;
legend('g(x)', 'y=x');
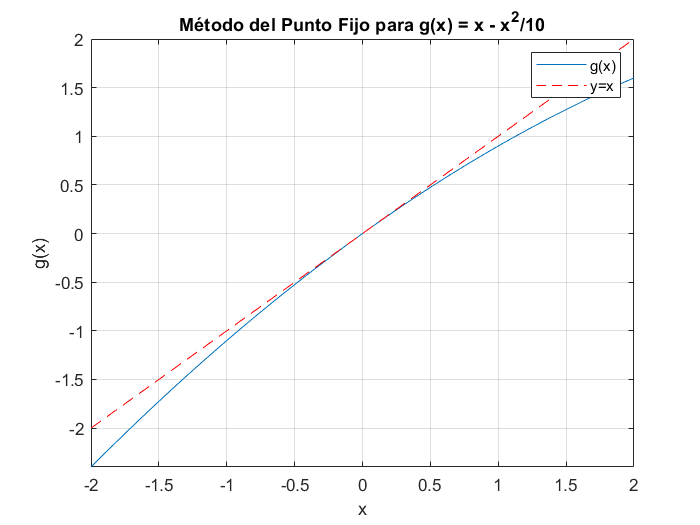
Aplicando a $g$ el método del punto fijo comenzando en $0.5$, se ve que después de 100 iteraciones, se llega a $0.0828$, un valor todavía alejado de la raíz 0.
x(1)=0.5;maxIter=100;
for k=2:maxIter
x(k)=g(x(k-1));
end
x(maxIter)
plot(1:maxIter,x,'o');
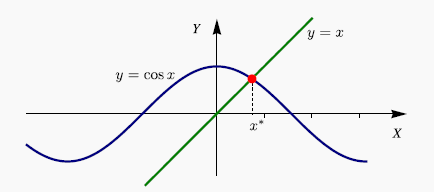
g=@(x) cos(x); xk=0.5;
format long
error=1;iter=0;
while error >10^-16
xk1=g(xk);
error=abs(xk-xk1);
xk=xk1;
iter=iter+1;
end
disp('Iteraciones')
iter
disp('Raiz')
xk
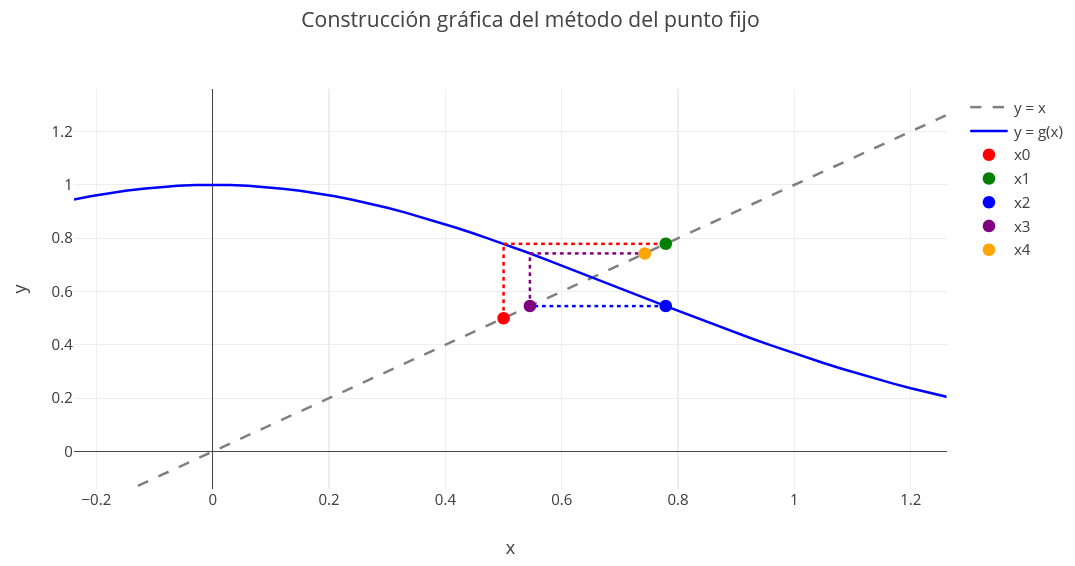
En el código siguiente se realizan hasta un máximo de iteraciones indicado en maxIter para conseguir la precisión dada.
% Se representa la función g y la recta y=x
g=@(x) exp(-x.^2);x=0:0.01:1;
plot(x,g1(x),x,x)
% Número máximo de iteraciones y tolerancia
xk=0.5;tol=10^-10;maxIter=100;format long
for k=1:maxIter
xk1=g(xk);
if abs(xk1-xk)<tol
xk=xk1; break
end
xk=xk1;
end
[xk g(xk) k]
Se puede ver que la función cumple la condición suficiente para asegurar la convergencia. Para ello basta calcular el máximo de $|g'|$ en $[0,1]$ que se alcanza en el punto $\sqrt{0.5}$, cumpliéndose
$$\left| {g'\left( x \right)} \right| = \left| { - 2x\,{e^{ - {x^2}}}} \right| < 1 \,\,\,\,\,\,\,\,\,x \in \left[ {0,1} \right]$$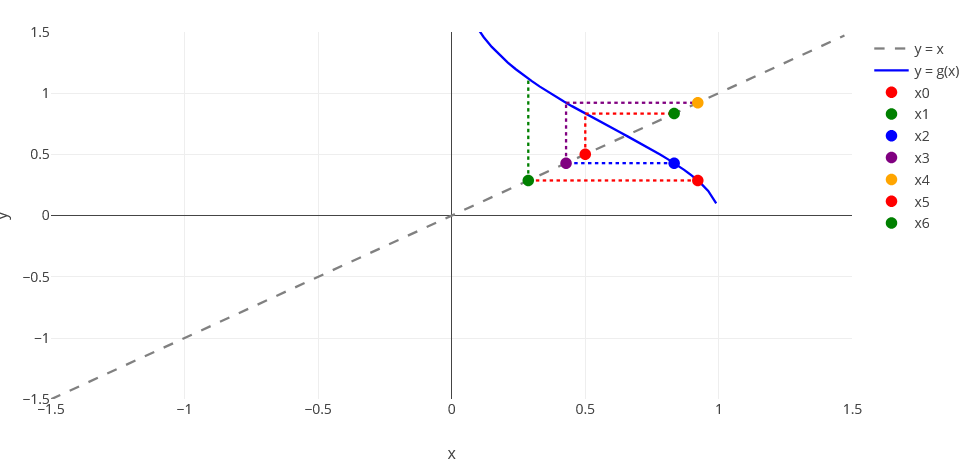
Con el siguiente código se pueden obtener las 5 primeras iteraciones. El valor absoluto de la derivada en $0.5$ no es menor que 1 por lo que no se tendría garantizada la convergencia comenzando a iterar en $0.5$.
h=@(x) (-log(x)).^0.5;
%Derivada
h1=@(x) -0.5*((-log(x)).^-0.5)./x;
h1(0.5) %-1.201122408786450
%Iteraciones
xk=0.5;
for k=1:5
xk=h(xk)
end
Se acotan en primer lugar los ceros de la función y se analiza qué funciones se pueden considerar para aplicar el punto fijo en cada intervalo.
Se tiene que $p'(x)=3x^2+6x=3x(x+2)$ tiene dos ceros en el punto 0 y en -2. En el punto $(0,-1)$ hay un mínimo y en el punto $(-2,3)$ un máximo. Luego $p$ tiene tres raíces reales. Aislando estas tres raíces, viendo intervalos donde hay cambio de signo, se tiene que están situadas en los intervalos [-3,-2], [-1,0], [0,1].
En la escena interactiva 3.5, se muestra paso a paso cómo generar el código de una
función Matlab/Octave: puntoFijo(g,x0, tol, maxiter) que tenga como argumentos la función g, el punto inicial x0, la
tolerancia tol y el número máximo de iteraciones maxiter.
Creada esta función, se calculan los tres ceros considerando una tolerancia por ejemplo de $10^{-6}$ y $100$ iteraciones como máximo, escribiendo el siguiente código en la ventana de comandos.
%Raiz en el intervalo [-3,-2]
g=@(x) x.^3-3;tol=10^-6;
puntoFijo(g,-2.5, tol, 100)
%Raíz en el intervalo [-1,0]
g=@(x) -sqrt((x+3)^-1); puntoFijo(g,-1.5, tol, 100)
%Raíz en el intervalo [0,1]
g=@(x) -sqrt((x+3)^-1); puntoFijo(g,0.5, tol, 100)
La idea de este método se basa en la aproximación lineal que proporciona la recta tangente. Una vez obtenido $x_k$, se calcula $x_{k+1}$ utilizando la aproximación lineal de $f(x)$ mediante la recta tangente que pasa por el punto $(x_k,f(x_k))$:
$$f(x) ≈ f(x_k )+f'(x_k)(x−x_k)$$Se toma $x_{k+1}$ como la intersección de esta recta con el eje de abscisas, es decir, la solución de
$$f(x_k ) + f'(x _k )(x − x_k ) = 0$$
Se toma el intervalo $[0,1]$ como el intervalo $[a,b]$ donde $f(a)f(b)< 0$. Además, en ese intervalo la derivada es estrictamente positiva por lo que la función es creciente y solo hay un cero. Como punto $x_0$, se considera el punto medio del intervalo $[0,1]$.
$x_0=0.5$
$x_1=x_0-\frac{x_0-cos(x_0)}{1+sen(x_0)}$ 0.755222417105636
$x_2=x_1-\frac{x_1-cos(x_1)}{1+sen(x_1)}$ 0.739141666149879
$x_3=x_2-\frac{x_2-cos(x_2)}{1+sen(x_2)}$ 0.739085133920807
$x_4=x_3-\frac{x_3-cos(x_3)}{1+sen(x_3)}$ 0.739085133215161
$x_5=x_4-\frac{x_4-cos(x_4)}{1+sen(x_4)}$ 0.739085133215161
El código Matlab/Octave a utilizar para calcular las cinco iteraciones es el siguiente:
x=0.5
for k=1:5
x=x-(x-cos(x))/(1+sin(x))
end
%Se puede ver que a partir de la cuarta iteración
%el resultado se estabiliza
El siguiente resultado establece que bajo ciertas condiciones sobre la función $f$, el método de Newton es convergente localmente con orden de convergencia cuadrático (de orden 2).
Se define la función y su derivada y se aplica el proceso iterativo del método de Newton.
f=@(x) exp(x)+2.^-x+2*cos(x)-6
df=@(x) exp(x)-log(2)*2.^-x-2*sin(x)
%Se busca un intervalo [a, b] con f(a)f(b) negativo
%Se toma [1,2] y se aplica el Método de Newton
x=1.5
x=x-f(x)/df(x)
%Esta última instrucción se repetiría hasta
%que x estabilice las 16 cifras decimales
En la siguiente tabla se muestran las primeras seis iteraciones viendo que se estabiliza a partir de la sexta iteración.
| $x_0$ | 1.500000000000000 | ||
| $x_1$ | 1.956489721124210 | $x_4$ | 1.829383614494166 |
| $x_2$ | 1.841533061042061 | $x_5$ | 1.829383601933849 |
| $x_3$ | 1.829506013203651 | $x_6$ | 1.829383601933849 |
Se puede observar, que en este caso, se duplica, aproximadamentemente, la cantidad de decimales de cada iteracion (convergencia cuadrática).
Para calcular la diferencia entre dos iteraciones se podría utilizar el siguiente código Matlab/Octave:
f=@(x) exp(x)+2^-x+2*cos(x)-6
df=@(x) exp(x)-2^-x*log(2)-2*sin(x)
x=1.5
x1=x-f(x)/df(x),error=abs(x-x1),x=x1;
%Se repetiría esta última línea de código
%para seguir iterando hasta conseguir
%la tolerancia deseada
f=@(x) exp(x)+2^-x+2*cos(x)-6
df=@(x) exp(x)+2^-x*log(2)-2*sin(x)
k=1; x(k)=1.5
x(k+1)=x(k)-f(x(k))/df(x(k))
error=abs(x(k)-x(k+1))
k=k+1;
%Se repetirían las tres últimas líneas de código
%para realizar una nueva iteración
polyval y polyder que, respectivamente, evalúan y derivan un polinomio definido a partir del vector de sus coeficientes.
p=[1 3 0 2]
dp=polyder(p) %polyder deriva el polinomio
%Se comprueba que hay cambio de signo en [-4,-2]
polyval(p,-4)*polyval(p,-2) %polyval evalúa un polinomio
x=-3
%Se aplica el método de Newton
x=x-polyval(p,x)/polyval(dp,x)
%Se repite este último paso para iterar
%sol=-3.195823345445647
Repitiendo el proceso con $x_0=1$, se puede ver que no converge, las iteraciones oscilan entre valores negativos y positivos. Esto ocurre porque el método de Newton converge localmente.
Para dejar de iterar, se pueden considerar distintos test de parada:
f, su derivada df, el punto inicial x0, el máximo de iteraciones maxiter y la tolerancia tol.
Newton(f,df, x0, tol, maxiter) que utiliza como método de parada que la
diferencia entre dos iteraciones consecutivas sea menor que la tolerancia fijada.
Para este método, se parte de un intervalo $[a,b]$ en el que $f(a)f(b) < 0$ y se toma como punto inicial $x_0=\frac{a+b}{2}$.
En cada iteración se busca una nueva aproximación $x_{k+1}$ y se actualizan $a$ y $b$ como se indica a continuación:
Debe tenerse en cuenta que no se aplicará el método de Newton cuando el denominador $f'(x_k)$ sea muy pequeño
(overflow), o cuando el cociente $\frac{f(x_k)}{f'(x_k)}$ sea muy grande. Es decir,
se utilizará el método de Newton cuando
$$\left|\frac{f(x_k)}{f'(x_k)}\right| <
\frac{1}{\epsilon_M}$$ Esta última condición se implementa de la forma siguiente y se comprueba antes de aplicar cada paso del método de Newton:
$$\left|{f'(x_k)}\right| > {\epsilon_M} |{f(x_k)}|$$
Se muestra a continuación el algoritmo aplicado a un ejemplo.
f=@(x) exp(x)+2.^-x+2*cos(x)-6
df=@(x) exp(x)-log(2)*2.^-x-2*sin(x)
f(1)*f(2) %Se comprueba cambio de signo
em=eps/2
a=1;b=2;fa=f(a);fb=f(b);x=(a+b)/2;fx=f(x);
[a x b],[fa fx fb]
| Punto inicial | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $1$ | $1.5$ | $2$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $-1.701113559804675$ | $-1.023283135733256$ | $0.806762425836365$ |
Para la siguiente iteración se debe considerar el nuevo intervalo o bien $[a,x]$, si $f(a) \cdot f(x) < 0$, o bien $[x,b]$ en caso contrario. A partir de los datos de la tabla anterior se toma $[a,b]=[1.5,2]$ que es donde hay cambio de signo. Antes de obtener la siguiente iteración se comprueba si la derivada toma valores pequeños.
a=x;fa=fx;m=df(x);
if abs(m)>em*abs(fx),x=x-fx/m;[a x b],end
fx=f(x); [fa fx fb]
| Iteración 1 | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $ 1.500000000000000$ | $1.956489721124211$ | $2.000000000000000$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $-1.023283135733256$ | $0.579701373274924$ | $0.806762425836365$ |
El valor de $x$ obtenido está en $[a,b]$, como además el cambio de signo de $f$ se produce en $[a,x]$, se toma para la siguiente iteración $[a,b]=[a,x]$.
b=x;fb=fx;m=df(x);
if abs(m)>em*abs(fx),x=x-fx/m,end
fx=f(x);[fa fx fb]
| Iteración 2 | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $ 1.500000000000000$ | $1.841533061042061$ | $1.956489721124211$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $-1.023283135733256$ | $0.050340951614865$ | $0.579701373274924$ |
El valor de $x$ obtenido está en $[a,b]$, como $f$ cambia de signo en $[a,x]$, se toma este intervalo para la siguiente iteración $[a,b]=[a,x]$.
b=x;fb=fx;m=df(x);
if abs(m)>em*abs(fx),x=x-fx/m,end
fx=f(x);[a x b],[fa fx fb]
| Iteración 3 | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $ 1.500000000000000$ | $1.829506013203651$ | $1.841533061042061$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $-1.023283135733256$ | $0.0005021213225915$ | $0.050340951614865$ |
De nuevo, el valor de $x$ está en $[a,b]$. Como $f$ cambia de signo en $[a,x]$, se toma $[a,b]=[a,x]$ para la siguiente iteración.
b=x;fb=fx;m=df(x);
if abs(m)>em*abs(fx),x=x-fx/m,end
fx=f(x);[a x b],[fa fx fb]
| Iteración 4 | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $ 1.500000000000000$ | $1.829383614494166$ | $1.829506013203651$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $-1.023283135733256$ | $0.000000051516139$ | $0.000502121322591$ |
De nuevo, el valor de $x$ obtenido está en $[a,b]$. Como el cambio de signo de $f$ es en $[a,x]$ se considera para la siguiente iteración $[a,b]=[a,x]$.
b=x;fb=fx;m=df(x);
if abs(m)>em*abs(fx),x=x-fx/m,end
fx=f(x);[a x b],[fa fx fb]
| Iteración 5 | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $ 1.500000000000000$ | $\mathbf{ \color{blue}1.829383601933849}$ | $1.829383614494166$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $-1.023283135733256$ | $0.000000000000001$ | $0.0000000515161391$ |
La solución es $x=1.829383601933849$. En este ejemplo, siempre el valor de $x$ obtenido ha estado en el intervalo por lo que en cada iteración se ha aplicado Newton.
Se definen los datos del problema.
f=@(x) exp(x)+2^(-x)+2*cos(x)-6
df=@(x) exp(x)-log(2)*2^(-x)-2*sin(x)
f(-3)*f(-2)
a=-3;fa=f(a);b=-2;fb=f(b);x=(a+b)/2;fx=f(x);em=eps/2;
[a x b],[f(a) f(x) f(b)]
| $a$ | $x$ | $b$ |
| $-3.000000000000000$ | $-2.500000000000000$ | $-2.000000000000000$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $0.069802075166974$ | $-1.863347982977588$ | $-2.696958389857672$ |
El cambio de signo ocurre en $[a,x]$, por lo que ese será el intervalo en la siguiente iteración. Se modifica el código del ejemplo anterior para comprobar, en cada paso, si el valor obtenido $x$ está en $[a,b]$; en tal caso se acepta, y si no, se aplica el método de bisección.
b=x;fb=fx;dfx=df(x);
if abs(dfx)>em*abs(fx)
x=x-fx/dfx;
if a<=x && b>=x
disp('Se aplica Newton');fx=f(x);
else
disp('Se aplica Biseccion');x=(a+b)/2;fx=f(x);
end
else
x=(a+b)/2;fx=f(x);
end
[a x b],[fa fx fb]
| Iteración 1 | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $-3.000000000000000$ | $-2.750000000000000$ | $-2.500000000000000$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $0.069802075166974$ | $-1.057505574028503$ | $-1.863347982977588$ |
Repitiendo el código en cada iteración y actualizando previamente el intervalo $[a,b]$ según se produzca cambio de signo de $f$ en los extremos de $[a,x]$ o de $[x,b]$, se obtiene la solución en 6 iteraciones. A continuación, se muestran los resultados de cada paso.
| Iteración 2: Bisección | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $-3.000000000000000$ | $-2.875000000000000$ | $-2.750000000000000$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $0.069802075166974$ | $-0.536899807501486$ | $-1.057505574028503$ |
| Iteración 3: Newton | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $-3.000000000000000$ | $-2.994267548648236$ | $-2.875000000000000$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $0.069802075166974$ | $0.040014356224199$ | $-0.536899807501486$ |
| Iteración 4: Newton | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $-2.994267548648236$ | $-2.986542066999646$ | $-2.875000000000000$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $0.040014356224199$ | $0.000174552940576$ | $-0.536899807501486$ |
| Iteración 5: Newton | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $-2.994267548648236$ | $2.986508070038639$ | $-2.875000000000000$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $0.000174552940576$ | $0.000000003371666$ | $-0.536899807501486$ |
| Iteración 6: Newton | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $-2.986508070038639$ | $\mathbf{ \color{blue} -2.986508069381928}$ | $-2.875000000000000$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $0.000000003371666$ | $0$ | $-0.536899807501486$ |
Después de las 6 iteraciones, el cero de $f$ en el intervalo $[-3,-2]$ es $-2.986508069381928$
f derivable con derivada df, en un intervalo donde la función cambie de signo, $[a,b]$, con una tolerancia tol establecida y un máximo de
iteraciones maxiter permitidas: NewtonBisección(f,df, a, b, tol, maxiter)
Con la herramienta siguiente se muestra cómo generar paso a paso el código Matlab/Octave de
la función NewtonBiseccion(f,df, a, b,tol, maxiter) que utiliza como método de
parada que la diferencia entre dos iteraciones consecutivas sea menor que la tolerancia
fijada.
El método de Newton tiene el problema de que podría darse “overflow” si se divide por un número muy pequeño, o dada su convergencia local, podría converger a otra raíz distinta de la buscada o incluso no converger. Además, al requerir la derivada de la función podría ser difícil de obtener por ejemplo en el caso de ciertas funciones como las definidas por integrales o por series infinitas.
En el siguiente apartado se muestra un método que no requiere la derivada de la función cuyo cero se quiere calcular.
Este método considera la aproximación que da la secante en intervalos pequeños en lugar de la recta tangente para aproximar la raíz.
Esta expresión se justifica considerando la recta secante que pasa por los puntos $(x_{k-1},f(x_{k-1}))$ y $(x_{k},f(x_{k}))$ y obteniendo el punto de corte de dicha recta con el eje $y=0$. La ecuación de la recta es
$$y = f\left( {{x_k}} \right) + {m_k}\left( {x - {x_k}} \right)\,\,\,\,\,\,\,\,\,\,\,\,{m_k} = {{f\left( {{x_k}} \right) - f\left( {{x_{k - 1}}} \right)} \over {{x_k} - {x_{k - 1}}}}$$y su punto de intersección con $y=0$ será el valor de $x_{k+1}$
$$0 = f\left( {{x_k}} \right) + {m_k}\left( {x - {x_k}} \right) \to \,\,{x_{k + 1}} = {x_k} - \frac{{f\left( {{x_k}} \right)}}{{{m_k}}}$$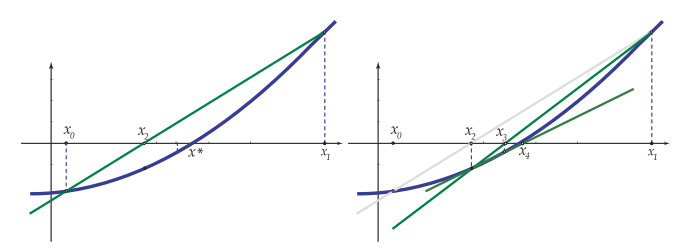
f, los puntos iniciales x0 y x1, la tolerancia tol y el número máximo de iteraciones permitidas maxiter .
Pulsando en el botón solución guiada del interactivo siguiente, se muestra la
programación de la función Secante(f, x0, x1, tol, maxiter).
Al igual que en el caso del método de Newton, resulta conveniente implementar este método combinado con el de bisección, para garantizar la convergencia en situaciones en las que la aproximación secante no sea válida o segura.
En el algoritmo, se parte de un intervalo $[a,b]$ donde $f(a)f(b)< 0$. Se toma $x_0=a$ y $x_1=b$.
En cada iteración, se busca una nueva aproximación $x_{k+1}$ y se actualiza $a$ y $b$ como se indica a continuación:
Tampoco se aplicará el método de la secante cuando el denominador $m_k$ sea muy pequeño o $\left|f(x_k)/m_k\right| > 1/\epsilon_M$. Se verificará por tanto que se cumple la siguiente condición antes de aplicar el método de la secante: $$|{m_k}| > {\epsilon_M} |{f(x_k)}|$$
Los tests de parada a utilizar son los mismos que en el caso del método de Newton-Bisección.
Se define $x_0=0$ y $x_1=1$ para empezar a iterar en el método de la secante y se calcula el siguiente valor $x$ utilizando el método de la secante comprobando si está en $[0,1]$.
em=eps/2;format long
f=@(x) erf(x)-0.5
f(0)*f(1)
a=0;b=1;fa=f(a);fb=f(b);x0=a;fx0=fa;x1=b;fx1=fb;
%Se calcula siguiente punto por el mét. de la secante
m=(fx1-fx0)/(x1-x0);
if abs(m)>em*abs(fx1)
x=x1-fx1/m;fx=f(x);
end
%El valor x está en [a,b], no se necesita bisección
[a x b],[f(a) fx f(b)]
| Iteración 1 | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $0$ | $0.593330401707401$ | $1.000000000000000$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $-0.500000000000000$ | $0.098584503929305$ | $0.342700792949715$ |
El cambio de signo se produce en $[a,x]$ por lo que se toma este intervalo como el nuevo $[a,b]$. Se actualiza $x_0$ y $x_1$ que serán respectivamente $x_1$ y $x$.
b=x;x0=x1;x1=x;fx0=f(x0);fx1=f(x1);
% Calculo del siguiente punto
m=(fx1-fx0)/(x1-x0);
if abs(m)>em*abs(fx1)
x=x1-fx1/m;fx=f(x);
end
[a x b],[f(a) fx f(b)]
% Se comprueba que x está en [a,b]
| Iteración 2 | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $0$ | $0.429099981968989$ | $0.593330401707401$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $-0.500000000000000$ | $-0.043957753989566$ | $0.342700792949715$ |
El punto $x$ está dentro del intervalo $[a,b]$. El cambio de signo se produce en $[x,b]$, se toma este intervalo como el nuevo $[a,b]$. Se actualiza $x_0$ y $x_1$ que serán respectivamente $x_1$ y $x$ para la siguiente iteración.
a=x;x0=x1;x1=x;fx0=f(x0);fx1=f(x1);
% Calculo del siguiente punto
m=(fx1-fx0)/(x1-x0);
if abs(m)>em*abs(fx1)
x=x1-fx1/m;fx=f(x);
end
[a x b],[f(a) fx f(b)]
%Se comprueba que está en [a,b]
| Iteración 3 | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $0.429099981968989$ | $0.479746018406641$ | $0.593330401707401$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $-0.043957753989566$ | $0.002522030582461$ | $0.098584503929305$ |
El punto $x$ está dentro del intervalo $[a,b]$. El cambio de signo se produce ahora en $[a,x]$, se toma este intervalo como el nuevo $[a,b]$. Se actualiza $x_0$ y $x_1$ que serán respectivamente $x_1$ y $x$ para la siguiente iteración.
b=x;x0=x1;x1=x;fx0=f(x0);fx1=f(x1);
m=(fx1-fx0)/(x1-x0);
if abs(m)>em*abs(fx1)
x=x1-fx1/m;fx=f(x);
end
[a x b],[f(a) fx f(b)]
%Se comprueba que está en [a,b]
| Iteración 4 | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $0.429099981968989$ | $0.476997923639157$ | $0.479746018406641$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $-0.043957753989566$ | $0.000055407570768$ | $0.002522030582461$ |
El punto $x$ se encuentra dentro del intervalo $[a,b]$. De nuevo, el cambio de signo de $f$ se produce en $[a,x]$. Se toma este intervalo como el nuevo $[a,b]$. Se actualiza $x_0$ y $x_1$ que serán respectivamente $x_1$ y $x$.
b=x;x0=x1;x1=x;fx0=f(x0);fx1=f(x1);
m=(fx1-fx0)/(x1-x0);
if abs(m)>em*abs(fx1)
x=x1-fx1/m;fx=f(x);
end
[a x b],[f(a) fx f(b)]
%Se comprueba que está en [a,b]
| Iteración 5 | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $0.429099981968989$ | $0.476936276206905$ | $0.476997923639157$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $-0.043957753989566$ | $-0.000000074435110$ | $0.000055407570768$ |
El cambio de signo de $f$ se produce en $[x,b]$. Se toma este intervalo como el nuevo $[a,b]$. Se actualiza $x_0$ y $x_1$ que serán respectivamente $x_1$ y $x$.
a=x;x0=x1;x1=x;fx0=f(x0);fx1=f(x1);
m=(fx1-fx0)/(x1-x0);
if abs(m)>em*abs(fx1)
x=x1-fx1/m;fx=f(x);
end
[a x b],[f(a) fx f(b)]
% Se comprueba que está en [a,b]
| Iteración 6 | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $0.476936193389100$ | $0.476936276206905$ | $0.476997923639157$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $1.0e-04 *$-0.000744351095761$ | $1.0e-04 *$$0.000000021886937$ | $1.0e-04 *$$0.554075707681623$ |
b=x;x0=x1;x1=x;fx0=f(x0);fx1=f(x1);
m=(fx1-fx0)/(x1-x0);
if abs(m)>em*abs(fx1)
x=x1-fx1/m;fx=f(x);
end
[a x b],[f(a) fx f(b)]
%Se comprueba que está en [a,b]
El valor de $x$ está en $[a,b]$. Como el cambio de signo de $f$ se produce en $[a,x]$, este intervalo será el nuevo intervalo $[a,b]$ para la siguiente iteración.
| Iteración 7 | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $0.476936193389100$ | $\mathbf{ \color{blue} 0.476936276204470}$ | $0.476936276206905$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $1.0e-07 *$-0.744351095760543$ | $1.0e-07 *$$0$ | $1.0e-07 *$$0.000021886936707$ |
Después de estas iteraciones, se obtiene el punto $0.476936276204470$ como aproximación de la raíz.
Dada la dificultad de calcular la derivada de $f(x)$, se utilizará el método de la secante.
Se define la función $f$ y se comprueba que en el intervalo $[1,2]$ hay cambio de signo.
%det(A-landa*I) landa=-2 valor propio
%f(x)=det(A(x)+2I)
f=@(x) det([x+2 2 -3 5 0 x^2;1 3 1 1 1 1;
0 x x+2 0 5 -2; 1 -1 1 1 2*x 0;
1 0 1 0 (x^2)+2 -2;0 0 1 0 cos(x) -x+2])
%Se buscan cambios de signo
% f(0)<0
% f(1)<0
% f(2)>0
% Hay otros intervalos donde la función cambia de
% signo pero solo piden calcular un valor de x
Se considera el intervalo $[a,b]=[1,2]$ y los puntos iniciales $x_0=1$, $x_1=2$ para empezar a iterar . Se calcula el punto $x_2$ si la aproximación por el método de la secante se encuentra en el intervalo $[a,b]$, o se utiliza bisección en caso contrario.
format long
em=eps/2;
a=1;b=2;x0=a;x1=b;fx0=f(x0);fx1=f(x1);
m=(fx1-fx0)/(x1-x0);
%Se aplica el método de la secante si
%la pendiente no es próxima a cero
if abs(m)>em*abs(fx1)
x=x1-fx1/m
end
[a x b]
%Se observa que x está dentro del intervalo [a,b]
fx=f(x);[fa fx fb]
| Iteración 1 | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $1.000000000000000$ | $1.264336373802500$ | $2.000000000000000$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $1.0e-02 *$-0.389735559513635$ | $1.0e-02 *$$0.168432357189391$ | $1.0e-02 *$$1.084656912121114$ |
El cambio de signo de $f$ es en $[a,x]$ por lo que este intervalo será el nuevo intervalo $[a,b]$ para la siguiente iteración. Se actualizan $x_0$ y $x_1$ que serán, respectivamente, $x_1$ y $x$.
b=x;fb=f(b);x0=x1;fx0=fx1;x1=x;fx1=fx;
m=(fx1-fx0)/(x1-x0);
if abs(m)>em*abs(fx1)
x=x1-fx1/m
end
%En este caso x está dentro del intervalo [a,b]
[a x b],fx=f(x);[fa fx fb]
| Iteración 2 | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $1.000000000000000$ | $1.184570415928323$ | $1.264336373802500$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $-38.973555951363515$ | $0.507113188549775$ | $16.843235718939074$ |
Se vuelve a producir un cambio de signo en $[a,x]$ por lo que ejecutando el mismo código anterior se obtienen los siguientes valores.
| Iteración 3 | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $1.000000000000000$ | $1.182094285551603$ | $1.184570415928323$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $-38.973555951363515$ | $-0.008881043100172$ | $0.507113188549775$ |
En este caso hay cambio de signo en $[x,b]$ por lo que el nuevo intervalo $[a,b]$ es $[x,b]$. Se actualizan $x_0$ y $x_1$ que serán, respectivamente, $x_1$ y $x$.
a=x;fa=f(a);x0=x1;fx0=fx1;x1=x;fx1=fx;
m=(fx1-fx0)/(x1-x0);
if abs(m)>em*abs(fx1)
x=x1-fx1/m
[a x b]
end
%En este caso x está dentro del intervalo [a,b]
[a x b],fx=f(x);[fa fx fb]
| Iteración 4 | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $1.182094285551603$ | $1.182136903509806$ | $1.184570415928323$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $-0.008881043100172$ | $0.000004066033751$ | $0.507113188549775$ |
En este caso hay cambio de signo en $[a,x]$ por lo que el nuevo intervalo $[a,b]=[a,x]$. Se actualizan $x_0$ y $x_1$ que serán, respectivamente, $x_1$ y $x$.
b=x;fb=f(b);x1=x;fx1=fx;
m=(fx1-fx0)/(x1-x0);
if abs(m)>em*abs(fx1)
x=x1-fx1/m
end
%En este caso x está dentro del intervalo [a,b]
[a x b],fx=f(x);[fa fx fb]
| Iteración 5 | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $1.182094285551603$ | $1.182136884006832$ | $1.182136903509806$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $-0.008881043100172$ | $0.000000000032507$ | $0.000004066033751$ |
Como vuelve a haber cambio de signo en el intervalo $[a,x]$ se ejecuta el mismo código anterior.
| Iteración 6 | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $1.182094285551603$ | $1.182136884006832$ | $1.182136903509806$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $-0.008881043100172$ | $0.000000000000003$ | $0.000000000032507$ |
Nuevamente vuelve a haber cambio de signo en $[a,x]$ por lo que se ejecuta el último código otra vez.
| Iteración 7 | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $1.182136884006676$ | $\mathbf{ \color{blue} 1.182136884006676}$ | $1.182136884006832$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $1.0e-10 *$$0.000025575661434$ | $1.0e-10 *$$0.000025575661434$ | $1.0e-10 *$$0.325066656820725$ |
En cada iteración el valor de $x$ calculado por el método de la secante ha cumplido que está en el intervalo $[a,b]$ por lo que no se ha aplicado bisección en ninguna iteración.
$Se establecen los datos del problema
f=@(x) exp(x)+2.^-x+2*cos(x)-5;
em=eps/2;
format long
a=-5;b=0;fa=f(a);fb=f(b);
x0=a;x1=b;fx0=fa;fx1=fb;
Se calcula el siguiente término de la sucesión, $x=x_2$, aplicando secante si el valor obtenido se encuentra en $[a,b]$ o, en caso contrario, utilizando bisección.
%Código cálculo siguiente término
m=(fx1-fx0)/(x1-x0);
if abs(m)>em*abs(fx1)
x=x1-fx1/m;
if a<=x & b>=x
disp('Se aplica secante')
else
disp('Se aplica biseccion')
x=(a+b)/2;
end
fx=f(x);
[a x b],[f(a) fx f(b)]
else
disp('División por cero')
end
| Iteración 1 | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $-5.000000000000000$ | $-0.174983869789607$ | $0$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $27.574062317925538$ | $-1.062118961781644$ | $-1.000000000000000$ |
Como hay cambio de signo en $[a,x]$ este será el nuevo intervalo $[a,b]$. Se modifica el intervalo y se cambia el valor de $x_0$ por $x_1$ y $x_1$ por $x$ para la próxima iteración.
b=x;
x0=x1;fx0=fx1;
x1=x;fx1=fx;
%Ejecutar después el código para calcular
%el siguiente término
| Iteración 2. Se aplica bisección | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $-5.000000000000000$ | $-2.587491934894803$ | $-0.174983869789607$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $27.574062317925538$ | $-0.615010653972961$ | $-1.062118961781644$ |
De nuevo el cambio de signo de $f$ es en $[a,x]$, por lo que este será el nuevo intervalo $[a,b]$. Se modifica el intervalo, se cambia el valor de $x_0$ por $x_1$ y $x_1$ por $x$ y se ejecuta después el código para calcular el siguiente término.
b=x;x0=x1;fx0=fx1;x1=x;fx1=fx;
%Ejecutar después el código para calcular
%el siguiente término
| Iteración 3. Se aplica bisección | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $-5.000000000000000$ | $-3.793745967447402$ | $-2.587491934894803$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $27.574062317925538$ | $7.301512320864664$ | $-0.615010653972961$ |
Ahora el cambio de signo de $f$ es en $[x,b]$, se cambia el intervalo $[a,b]$ y los valores de $x_0$ y $x_1$.
a=x;x0=x1;x1=x;fx0=fx1;fx1=fx;
%Ejecutar después el código para calcular
%el siguiente término
| Iteración 4. Se aplica secante | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $-3.793745967447402$ | $-2.681202151333973$ | $-2.587491934894803$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $7.301512320864664$ | $-0.309376060449428$ | $-0.615010653972961$ |
El intervalo donde cambia de signo $f$ es $[a,x]$, se cambia el intervalo $[a,b]$ y se actualiza $x_0$ y $x_1$ para la próxima iteración.
b=x;x0=x1;x1=x;fx0=fx1;fx1=fx;
%Ejecutar después el código para calcular
%el siguiente término
| Iteración 5. Se aplica secante | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $-3.793745967447402$ | $-2.726426099664577$ | $-2.681202151333973$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $7.301512320864664$ | $-0.146504190440662$ | $-0.309376060449428$ |
De nuevo el intervalo donde cambia de signo $f$ es $[a,x]$, se cambia el intervalo $[a,b]$ y se actualiza $x_0$ y $x_1$ para la próxima iteración.
b=x;x0=x1;x1=x;fx0=fx1;fx1=fx;
%Ejecutar después el código para calcular
%el siguiente término
| Iteración 6. Se aplica secante | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $-3.793745967447402$ | $-2.767105303128926$ | $-2.726426099664577$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $7.301512320864664$ | $0.008859811280272$ | $-0.146504190440662$ |
El cambio de signo $f$ es en $[x,b]$, se cambia el intervalo $[a,b]$ y se actualiza $x_0$ y $x_1$ para la próxima iteración.
a=x;x0=x1;x1=x;fx0=fx1;fx1=fx;
%Ejecutar después el código para calcular
%el siguiente término
| Iteración 7. Se aplica secante | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $-2.767105303128926$ | $-2.764785524662011$ | $-2.726426099664577$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $0.008859811280272$ | $-0.000229260174994$ | $-0.146504190440662$ |
El cambio de signo de $f$ es $[a,x]$, se cambia el intervalo $[a,b]$ y se actualiza $x_0$ y $x_1$ para la próxima iteración.
b=x;x0=x1;x1=x;fx0=fx1;fx1=fx;
%Ejecutar después el código para calcular
%el siguiente término
| Iteración 8. Se aplica secante | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $-2.767105303128926$ | $ -2.764844038099813$ | $-2.764785524662011$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $0.008859811280272$ | $-0.000000343381642$ | $-0.000229260174994$ |
De nuevo, el cambio de signo de $f$ es en $[a,x]$, se cambia el intervalo $[a,b]$ y se actualiza $x_0$ y $x_1$ para la próxima iteración.
b=x;x0=x1;x1=x;fx0=fx1;fx1=fx;
%Ejecutar después el código para calcular
%el siguiente término
| Iteración 9. Se aplica secante | ||
|---|---|---|
| $a$ | $x$ | $b$ |
| $-2.767105303128926$ | $\mathbf{ \color{blue} -2.764844125871619}$ | $-2.764844038099813$ |
| $f(a)$ | $f(x)$ | $f(b)$ |
| $0.008859811280272$ | $0.000000000013341$ | $-0.000000343381642$ |
Después de las iteraciones realizadas, la raiz de la función $f$ en $[-5,0]$ con la tolerancia indicada es $-2.764844125871619$.
f, dos puntos imiciales donde la función cambie de signo a y b, la tolerancia tol y maxiter el máximo de
iteraciones permitidas: SecanteBiseccion(f, a, b, tol, maxiter)
Con la herramienta siguiente se muestra cómo generar paso a paso el código Matlab/Octave de
la función SecanteBiseccion(f, a, b, tol, maxiter) que utiliza como método
de parada que la diferencia entre dos iteraciones consecutivas sea menor que la tolerancia
fijada.
En este apartado, se analizará el problema de encontrar todas las raíces (reales y complejas) de un polinomio, es decir, se presentará un método para calcular todas las soluciones de
$${a_o} + {a_1}x + {a_2}{x^2} + ... +{a_n}{x^n} = 0$$Se recuerdan los siguientes resultados que aplican a los polinomios:
Aunque inicialmente se ha descrito el método de Newton para calcular las raíces de una ecuación $f(x)=0$ siendo $f$ una función real de variable real, el método también es válido para encontrar raíces de funciones complejas. Además, como la derivada de un polinomio es fácilmente calculable, el método de Newton resulta adecuado para calcular las raíces de un polinomio.
Una primera idea sería
Otra posibilidad, podría ser considerar el polinomio resultado de
El método que se utiliza para encontrar una nueva raíz de un polinomio, cuando se han calculado ya otras previamente, es el
Derivando $f_m$ y operando, se puede llegar a la siguiente expresión que es la que se considera directamente:
$${{{f_m}\left( x \right)} \over {f{'_m}\left( x \right)}} = {{p\left( x \right)} \over {p'\left( x \right) - p\left( x \right)\sum\limits_{j = 1}^m {{1 \over {x - {\alpha _j}}}} }}$$Para aplicar este método, se debe tener en cuenta lo siguiente:
Como se ha visto anteriormente, el método de Newton converge cuadráticamente hacia una raíz $\alpha$ si
$p'(\alpha)\ne0$.
Si la convergencia siguiera siendo lenta, entonces se aplicaría el método de Newton a la segunda derivada para ver si la raíz es doble, o a derivadas sucesivas en el caso en el que la multiplicidad sea mayor.
Si se calcula una raíz $\alpha$ de $p'(x)$ (o de derivadas sucesivas de p) y se observa que $$\left| {p\left( \alpha \right)} \right| \gg \left| {p'\left( \alpha \right)} \right|$$ entonces se debe concluir que $\alpha$ no es raíz de $p$, lo que ocurre es que $p$ posee dos o más raíces muy próximas. En el caso de que haya raíces próximas entonces la convergencia será lenta y, en general, no se podrá obtener una precisión alta en la solución.
En los siguientes ejemplos se verá cómo aplicar el método de Maehly para encontrar todas las raíces de un polinomio utilizando el fichero itraiz.m que realiza una iteración de este método. Los parámetros de los que depende son los coeficientes del polinomio cuya raíz se quiere calcular, los coeficientes del polinomio derivada, el vector con las raíces ya calculadas y el punto a partir del cual se va a iterar.
%Se define el polinomio a partir de sus coeficientes
p=[8 26 54 27 -128 -576 -864 -432]
%Se calcula su derivada
dp=polyder(p)
%Se inicializa el vector donde se almacenarán
%las raíces cuando se vayan obteniendo
v=[],x=i;
format long
x=itraiz(p,dp,v,x)
%Se hacen iteraciones hasta encontrar la primera raíz
%aplicando x=itraiz (p,dp,v,x) hasta que x se
%estabilice
%Se comprueba con: polyval(p,x)
x=
-1.056847723228969 + 0.262522264027478i
%Como la raiz obtenida x es compleja se incluye
%en v tanto x como su conjugada
v=[x;conj(x)]
%Se aplica el método con el vector v modificado
x=i;x=itraiz (p,dp,v,x)
%Se itera hasta que x se estabilice
%aplicando x=itraiz (p,dp,v,x)
x=
-1.540661467764130 + 1.474052474547216i
%Raiz compleja, se incluye en v tanto x como su conjugada
v=[v;x;conj(x)]
x=i;x=itraiz(p,dp,v,x)
%Se itera hasta que x se estabilice
%aplicando x=itraiz (p,dp,v,x)
x=
-0.059269229873907 + 2.202319797999819i
%La raíz es compleja, se incluye en v
%tanto x como su conjugada
v=[v;x;conj(x)]
%Se aplica el método para encontrar una nueva raíz
x=i;x=itraiz(p,dp,v,x)
%Se itera hasta encontrar la raiz
%Se comprueba que es raíz del polinomio
x=
2.063556841734012
%La raíz es real, se incluye en v
v=[v;x]
Se termina de iterar al haber encontrado las siete raíces del polinomio:
v =
-1.056847723228969 + 0.262522264027478i
-1.056847723228969 - 0.262522264027478i
-1.540661467764130 + 1.474052474547216i
-1.540661467764130 - 1.474052474547216i
-0.059269229873907 + 2.202319797999819i
-0.059269229873907 - 2.202319797999819i
2.063556841734012 + 0.000000000000000i
Encuentra una raíz de \(x = \frac{1}{2} sen(x) + \frac{1}{4}\) en el intervalo \([0, \pi/2]\) utilizando el método del punto fijo con un error absoluto de $10^{-16}$. Determina previamente que la raíz es única en dicho intervalo.
Resuelve \(f(x) = x^2 - e^{-x} = 0\), en el intervalo \([0,1]\) usando el método del punto fijo considerando el problema \(x = g(x)\) con \(g(x)\) las funciones siguientes:
Empezando la iteración con \(x_0 = 0.5\), realiza 100 iteraciones y analiza los resultados. Dibuja en el mismo gráfico la función \(f\) y las dos elecciones de \(g\) con la recta \(y = x\) junto con la localización de la raíz.
Encuentra una raíz de $x^3 - x - 2 = 0$ en el intervalo \([1, 2]\) utilizando el método de bisección y el método del punto fijo. Compara ambos métodos.
Implementa el método de la bisección para resolver la ecuación no lineal \(f(x) = \frac{1}{\pi} \int_0^x e^{t^2} dt - \frac{3}{4} = 0\) con un error absoluto \( \epsilon_a = 10^{-10}\)
Nota: Utiliza el comando integral para definir la función $f$.
En la mecánica celeste, la ecuación de Kepler para la anomalía excéntrica \(E\) de una órbita elíptica es:
\[ E - e\,\sin(E) \;-\; M \;=\; 0, \]
donde el parámetro excentricidad \(e\) y la anomalía media \(M\) se conocen. Se toma \(e = 0.8\) y \(M = 1.0\) (en radianes). Aplica el método de Newton para aproximar la solución \(E\), partiendo de la aproximación inicial \(E_0 = M\). Explica el comportamiento de las iteraciones y determina \(\,E\) con una tolerancia de \(10^{-10}\).
Un puente colgante sigue la ecuación de la catenaria:
\(y(x) = a \cosh\!\bigl(\tfrac{x}{a}\bigr) + C.\)
El punto más bajo del cable está en \(x = 0\), y se quiere que ese punto esté a 20 m sobre el terreno (es decir, \(y(0) = 20\)). Las torres, situadas a \(x = \pm 100\), tienen una altura de 100 m (medida desde el mismo nivel del terreno).
En consecuencia, si \(y(0) = a \cosh(0) + C = a + C = 20\), se obtiene \(C = 20 - a\). Además, en \(x = 100\) se debe cumplir
\(y(100) = a \cosh\!\bigl(\tfrac{100}{a}\bigr) + C = 100.\)
Reemplazando \(C = 20 - a\), se llega a la ecuación no lineal para \(a\):
\(\displaystyle a\,\cosh\!\bigl(\tfrac{100}{a}\bigr)\;+\;(20 - a)\;=\;100 \quad\Longleftrightarrow\quad a\Bigl[\cosh\!\bigl(\tfrac{100}{a}\bigr) - 1\Bigr] \;=\; 80.\)
Determina \(a\) con tolerancia \(10^{-10}\) usando el método de Newton.
Una empresa enfrenta una demanda exponencial: el precio de venta \(P(x)\) (en unidades monetarias por producto) cuando produce \(x\) unidades viene dado por
\(P(x) = 200\,e^{-0.01\,x}.\)
Su costo de producción es
\(C(x) = 50 + 10\,x + 0.05\,x^2.\)
Los ingresos son \(R(x) = x\,P(x) = 200\,x\,e^{-0.01\,x}\), y el beneficio \(\pi(x)\) es \(R(x) - C(x)\). Como la condición de primer orden para el máximo conduce a una ecuación trascendental
\(\frac{d\pi}{dx} = 0 \;\Longleftrightarrow\; 200\,e^{-0.01x}\bigl(1 - 0.01x\bigr) \;-\; \bigl(10 + 0.1x\bigr) = 0,\)
no se resuelve de forma cerrada. Se pide usar el método de Newton para hallar \(x^*\) que maximiza \(\pi(x)\), con tolerancia \(10^{-10}\).
Considere la función
\(f(x) = 0.2\,\sin(16x) \;-\; x \;+\; 1.75.\)
Se sabe que \(f(x)\) cambia de signo en el intervalo \([1,2]\), de modo que existe una raíz real \(x^* \in [1,2]\). Comprueba que si se intenta iniciar el método de Newton en \(x_0 = 1\), las iteraciones divergen. En cambio, aplicando el método de bisección en \([1,2]\) se aproxima la solución.
Se supone que la oscilación de una estructura, dotada de un sistema de amortiguación, ante un movimiento oscilatorio, viene dada por \(y(t) = 10 e^{-t/2}\cos(2t)\). ¿En qué instante \(t\) la posición de la estructura es \(y(t) = 4\)?
Se puede calcular la raíz n-ésima de un número \(a\) resolviendo la ecuación \(x^n - a = 0\). Implementa el método de Newton para obtener \(\sqrt[3]{345}\) con 7 cifras decimales exactas, partiendo del valor inicial \(x_0 = 2\).
Encuentra las dos raices reales de la ecuación:
$$200 \;=\; 100\,\cosh\bigl(x/0.5\bigr) \;+\; 20\,\sinh\bigl(x/0.5\bigr)$$ en el intervalo $[-2,2]$. Utiliza un error absoluto de $10^´{-10}$.La función de error \(erf(x) = \frac{2}{\sqrt{\pi}} \int_0^x e^{-t^2} dt\) está definida para \(x \geq 0\). Determina el valor de \(x\) tal que \(erf(x) = 0.5\).
Nota: Utiliza la función de Matlab erf para evaluar las integrales.
En un intercambiador de calor, la temperatura de salida \(T_s\) satisface la ecuación:
$$ T_s = T_e + (T_i - T_e)e^{-\frac{UA}{mc_p}} $$donde \(T_e = 20°C\) es la temperatura exterior, \(T_i = 80°C\) es la temperatura inicial, \(U = 200\, W/(m^2\cdot K)\) es el coeficiente global de transferencia de calor, \(m = 2\, kg/s\) es el flujo másico, $A$ es el área de intercambio térmico (superficie) del intercambiador de calor y \(c_p = 4186\, J/(kg\cdot K)\) es el calor específico. Si se desea una temperatura de salida de \(T_s = 35°C\), ¿cuál debe ser el área \(A\)?
La velocidad \(v\) de un paracaidista que cae está dada por \(v = \frac{mg}{c}(1 - e^{-ct/m})\). Para un paracaidista con coeficiente de arrastre \(c = 15\, \mathrm{kg/s}\), calcula la masa \(m\) de modo que la velocidad sea \(v = 126\, \mathrm{km/h}\) en \(t = 9\, \mathrm{s}\). Considera \( g = 9.81 m/s^2\).
Dada la ecuación \(2e^x - x^2 - 1 = 0\):
En un canal trapezoidal, la profundidad crítica \(y_c\) satisface la ecuación:
$$ \frac{Q^2}{g} = \frac{(by + my^2)^3}{b + 2y\sqrt{1+m^2}} $$donde \(Q = 2\, m^3/s\) es el caudal, \(g = 9.81\, m/s^2\) es la gravedad, \(b = 1\, m\) es el ancho del fondo, y \(m = 1\) es la pendiente lateral. Encuentra \(y_c\).
Se considera la ecuación \(\det(A(x)) = 0\), donde \(x\) es un número real y \(A(x)\) es la matriz:
\[ A(x) = \begin{pmatrix} \cos(x) & 1 & 2 & 3 \\ 0 & 1 & 0 & 1 \\ x & 2 & 3 & 4 \\ \sin(x) & x & 1 & \cos(x) \end{pmatrix} \]
Encuentra una raíz de \(f(x) = \det(A(x)) = 0\) en el intervalo \([0, 1]\).
Para la función \(f(x) = xe^x - 1\):
Utiliza el método de la secante para resolver \(f(x) = 100x^5 - 3995x^4 + 79700x^3 - 794004x^2 + 3160075x - 0\) en el intervalo \([17, 22.2]\) con un error absoluto y relativo de \(10^{-7}\). Realiza los cálculos considerando como puntos iniciales \(x_0 = 17\) y \(x_1 = 22.2\) y observa que no converge. Sin embargo, comprueba que sí converge si $x_0=22.2$ y $x_1=17$. ¿Qué justificación se puede dar?
Utiliza el método de Maehly para hallar todas las soluciones de las siguientes ecuaciones:
¿Cuántas raíces tiene cada ecuación? Comprueba los resultados con el comando
roots de Matlab.
Además, se discuten estrategias para la localización y separación de raíces, haciendo hincapié en la importancia de una elección adecuada del intervalo inicial y de las aproximaciones iniciales para garantizar la precisión en la obtención de soluciones numéricas.
Los aspectos clave en el estudio de los métodos numéricos de este tema son:

El ajuste por polinomios, en el contexto de los métodos numéricos, consiste en determinar un polinomio de grado adecuado que reproduzca con el menor error posible un conjunto de datos, ya sea obtenido mediante muestreo, experimentación o proveniente de una función analítica. Al expresar la información mediante una fórmula polinómica, se facilitan operaciones como el cálculo de valores intermedios, la interpolación y la predicción de comportamientos futuros.
Se supone por ejemplo que se tiene una tabla que relaciona la viscosidad dinámica del agua con la temperatura
| T ºC | 0 | 5 | 10 | 20 |
| $\mu_o$ | 1.787 | 1.519 | 1.307 | 1.002 |
¿Cómo estimar la viscosidad a una temperatura de 7.5º? Una opción es encontrar un polinomio que pase por los puntos de la tabla y estimar después el valor de 7.5 con él.
En este capítulo se presentarán dos técnicas para aproximar una función mediante un polinomio: la interpolación, que ajusta el polinomio pasando exactamente por los datos, y la aproximación por mínimos cuadrados, que busca minimizar el error global cuando no es posible (o deseable) que el polinomio pase por todos los puntos. Para más información, se puede consultar
El método de interpolación de Lagrange es una técnica que permite encontrar un polinomio que pasa exactamente por un conjunto de puntos dados.
 Joseph
Louis Lagrange (1736-1813) fue uno de los más grandes matemáticos de su tiempo. Nació en
Italia pero se nacionalizó Francés. Hizo grandes contribuciones en todos los campos de la
matemática y también en mecánica. Su obra principal es la “Mécanique analytique”(1788). En
esta obra de cuatro volúmenes, se ofrece el tratamiento más completo de la mecánica clásica
desde Newton y sirvió de base para el desarrollo de la física matemática en el siglo
XIX.
de una función $f$ definida en $[a,b]$ es el polinomio de grado menor o igual a $n$ que cumple
$p(x_i)=f(x_i)$ para cada $i$ entre $0$ y $n$. A los puntos ${x_0,x_1,...,x_n}$ se les llama
Joseph
Louis Lagrange (1736-1813) fue uno de los más grandes matemáticos de su tiempo. Nació en
Italia pero se nacionalizó Francés. Hizo grandes contribuciones en todos los campos de la
matemática y también en mecánica. Su obra principal es la “Mécanique analytique”(1788). En
esta obra de cuatro volúmenes, se ofrece el tratamiento más completo de la mecánica clásica
desde Newton y sirvió de base para el desarrollo de la física matemática en el siglo
XIX.
de una función $f$ definida en $[a,b]$ es el polinomio de grado menor o igual a $n$ que cumple
$p(x_i)=f(x_i)$ para cada $i$ entre $0$ y $n$. A los puntos ${x_0,x_1,...,x_n}$ se les llama
El video siguiente muestra un ejemplo práctico que calcula los polinomios base de Lagrange con tres nodos.
Los datos son:
$$\color{red}{x_o = - 1}\,\,\,\,\,\,\,\,\,\,\color{blue}{x_1 = 1}\,\,\,\,\,\,\,\,\,\,\,\color{green}{x_2 = 2}$$ $$f\left( {{x_o}} \right) = 2\,\,\,\,\,\,\,\,\,\,f\left( {{x_1}} \right) = 1\,\,\,\,\,\,\,\,\,\,f\left( {{x_2}} \right) = 1$$Los polinomios base de Lagrange son:
$$\begin{array}{lll} {l_o}\left( x \right) & = \frac{{x - {\color{blue}{1}}}}{{{\color{red}{-1}} - {\color{blue}{1}}}} \cdot \,\frac{{x - {\color{green}{2}}}}{{{\color{red}{-1}} - {\color{green}{2}}}} \\ \\ & = \frac{1}{6}\left( {{x^2} - 3x + 2} \right) = \frac{1}{6}{x^2} - \frac{1}{2}x + \frac{1}{3} \end{array}$$ $$\begin{array}{lll} {l_1}\left( x \right) & = \frac{{x - \left( { {\color{red}{-1}}} \right)}}{{{\color{blue}{1}} - \left( { {\color{red}{-1}}} \right)}} \cdot \frac{{x - {\color{green}{2}}}}{{{\color{blue}{1}} - {\color{green}{2}}}} \\ \\ & = - \frac{1}{2}\left( {x + 1} \right)\left( {x - 2} \right) = - \frac{1}{2}{x^2} + \frac{1}{2}x + 1 \end{array}$$ $$\begin{array}{lll} {l_2}\left( x \right) & = \frac{{x - \left( {{\color{red}{-1}}} \right)}}{{{\color{green}{2}} - \left( { {\color{red}{-1}}} \right)}} \cdot \frac{{x - {\color{blue}{1}}}}{{{\color{green}{2}} - {\color{blue}{1}}}} \\ \\ & = \frac{1}{3}\left( {x + 1} \right)\left( {x - {\color{blue}{1}}} \right) = \frac{1}{3}{x^2} - \frac{1}{3} \end{array}$$El polinomio interpolador es:
$$p\left( x \right) = f(x_o){l_0}\left( x \right) + f(x_1){l_1}\left( x \right) + f(x_2){l_2}\left( x \right) =$$ $$p\left( x \right) = 2\,{l_0}\left( x \right) + {l_1}\left( x \right) + {l_2}\left( x \right) = $$ $$={1 \over 6}{x^2} - {1 \over 2}x + {4 \over 3}$$Se puede comprobar que el polinomio coincide con la función en los nodos (ver figura 4.2):
$$p\left( { - 1} \right) = 2\,\,\,\,\,\,\,\,\,\,p\left( 1 \right) = 1\,\,\,\,\,\,\,\,\,\,p\left( 2 \right) = 1$$
x, y para incluir las coordenadas de los nodos de interpolación.
function p=polinomioLagrange(x,y)
% Se parte de un vector x e y de igual
% dimensión en los que se incluye las abscisas
% y ordenadas de los nodos
n = length(x);
% Se inicializa el polinomio resultante
p = zeros(1, n);
for i = 1:n
%Contrucción de li
% Índices de todos los puntos salvo el i-ésimo
indices = [1:i-1, i+1:n];
% Construye el numerador de li
li_num = poly(x(indices));
% Calcula el denominador de li
li_denom = polyval(li_num, x(i));
% Obtiene el polinomio base Li(t)
li = li_num/li_denom;
% Suma y_i·li(t) al polinomio total
p = p + y(i) * li;
end
end
Para obtener el polinomio del ejercicio 4.1 habría que escribir:
x=[-1,1,2];y=[2,1,1];
format rat
p=polinomioLagrange(x,y)
La fórmula para calcular el polinomio de Lagrange a partir de los polinomios base posee un interés teórico, pero existen otras formas de obtener en la práctica el polinomio interpolador. Una de ellas se muestra a continuación.
Se consideran los nodos ${x_0,x_1,...,x_n}$. Como se quiere calcular $p(x) = {a_o} + {a_1}x + ... + {a_n}{x^n}$ de forma que $p({x_i}) = f\left( {{x_i}} \right)$, se tendrá que cumplir que:
$$\begin{pmatrix} {x_{o}^n}&{x_{o}^{n-1}}&{...}&{x_0}&{1}\\ {{x_{1}^n}}&{{x_{1}^{n-1}}}&{...}&{x_{1}}&{1}\\ {...}&{...}&{...}&{...}&{...}\\ {{x_{n-1}^n}}&{{x_{n-1}^{n-1}}}&{...}&{x_{n-1}}&{1}\\ {{x_{n}^n}}&{{x_{n}^{n-1}}}&{...}&{x_{n}}&{1}\\ \end{pmatrix} \begin{pmatrix} {a_n} \\ {a_{n-1}} \\ {...}\\ {a_1}\\ {a_0} \end{pmatrix} = \begin{pmatrix} {f\left( {{x_o}} \right)}\\ {f\left( {{x_1}} \right)}\\ {...}\\ {f\left( {{x_{n-1}}} \right)}\\ {f\left( {{x_n}} \right)} \end{pmatrix}$$El método consiste en construir la matriz $A$ de orden $(n+1)$, el vector b de $\mathbb{R}^n$ y resolver el sistema $Aa=b$, donde $a$ es el vector de los coeficientes del polinomio. La matriz $A$ es invertible La matriz A es de Vandermonde ya que presenta una progresión geométrica en cada fila. Esta matriz es invertible si y solo si todos los $x_i$ son distintos entre sí. y el problema de interpolación de Lagrange tiene una única solución.
x=[-1 1 2]';b=[2 1 1]';n=2;
A=ones(n+1,1);t=A;
for k=1:n
t=t.*x; A=[t,A];
end
a=A\b %Solución p(x)=0.1667 x^2 - 0.5 x + 1.3333
%Comprobación
polyval(a,x)
vander halla la matriz A de Vandermonde a partir de los nodos $x_i$. También puede obtenerse la matria A con el código x.^(n:-1:0).
x=[-1 1 2]';A=vander(x)
%También A=x^(2:-1:0)
%Con n=5
n=5;a=0;b=1;x=linspace(a,b,n+1)';
fx=f(x);
A=[x ones(n+1,1)];t=x;
for iter=1:n-1
t=t.*x;
A=[t A];
end
p=A\fx;
%Se representa la función y el polinomio
s=linspace(a,b,500)';
fs=f(s);ps=polyval(p,s);
plot(s,[ps fs])
% En valor absoluto el máximo de la diferencia
% entre el polinomio y la función en los puntos x
max(abs(ps-fs))
% Considerando n=10 la diferencia es
% 1.794120407794253e-13
% Considerando n=15 la diferencia es
% 1.110223024625157e-14
En el ejemplo anterior, se ha obtenido una estimación del error evaluando la función y el polinomio en puntos del intervalo y calculando su valor máximo, en el siguiente apartado se da una expresión de la cota del error de la interpolación.
El error de interpolación mide la diferencia entre la función real y el polinomio interpolante, proporcionando una estimación cuantitativa de la precisión de la aproximación.
Como el polinomio de interpolación es de grado $n=2$, se llama $M$ al valor absoluto máximo de $f'''$ en el intervalo. Se tendrá que para cada $x$ en $[-1,2]$ se cumple,
$$\left| {f\left( x \right) - p\left( x \right)} \right| \le {M \over {3!}}\left| {\left( {x - {x_o}} \right)\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)} \right|$$ $$\left| {f\left( x \right) - p\left( x \right)} \right| \le {M \over {3!}}\left| {\left( {x + 1} \right)\left( {x - 1} \right)\left( {x - 2} \right)} \right|$$Para obtener una cota en el intervalo $[-1,2]$, se puede considerar el polinomio $q(x)=(x+1)(x-1)(x-2)$, calcular después los ceros de su derivada y tomar finalmente el mayor valor de $|q|$ en ellos.
format long
q=poly([-1 1 2]);dq=polyder(q);
r=roots(dq);%Máximos y mínimos de q
v=polyval(q,r);max(abs(v)) %2.112611790922380
Una cota del error en funcion de $M$ será entonces:
$$M\cdot 2.112611790922380/6$$Según la expresión del error, en un punto $x$ entre $0$ y $\pi$ se tendrá:
\[\left| {sen\left( x \right) - p\left( x \right)} \right| \leqslant \frac{{\mathop {\max }\limits_{c \in \left[ {0,\pi } \right]} \left| {{f^{'''}}\left( c \right)} \right|}}{{3!}}\,\left| {x - 0} \right|\left| {x - \frac{\pi }{2}} \right|\left| {x - \pi } \right|\] $$ \le \frac{1}{{3!}}\left| {x - 0} \right|\left| {x - \frac{\pi }{2}} \right|\left| {x - \pi } \right|$$Sustituyendo $x$ por $\pi/4$ se encontraría una cota de valor: $0.2422$. Para encontrar una cota en todo el intervalo, se considera el polinomio $q(x)=x(x-\pi/2)(x-\pi)$ y se calculan sus máximos y mínimos, esto es, las raíces de la derivada. El valor máximo en valor absoluto de $q$ en estos puntos será una cota de $\left| {q\left( x \right)} \right|$.
format long
q=poly([0 pi/2 pi]);dq=polyder(q);
r=roots(dq);v=polyval(q,r);max(abs(v)) %1.491790182328260
Una cota del error en $[0,\pi]$ sería entonces,
$$\left| {sen\left( x \right) - p\left( x \right)} \right| \le \frac{1}{{3!}}\left| {x - 0} \right|\left| {x - \frac{\pi }{2}} \right|\left| {x - \pi } \right| \le \frac{{1.492}}{6} \approx {\rm{0.248632}}$$Dado que en este ejemplo se conoce la función, se calculará una estimación del error de la aproximación entre la función y el polinomio interpolante evaluando en varios puntos y calculando el máximo de la diferencia entre $f$ y $p$ en todos ellos.
format long
%a es el polinomio interpolante
v=linspace(0,pi,300);
max(abs(polyval(a,v)-sin(v)))
%0.248631697054710
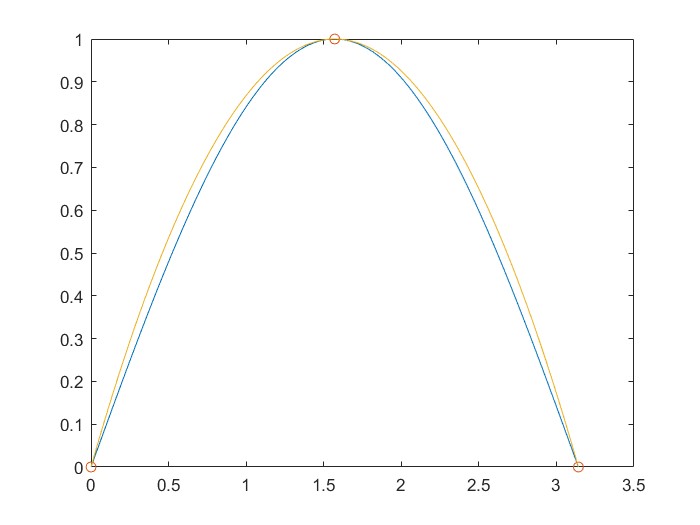
Se escribe el código para resolver el problema.
% Función log(x)
format long
f=@(x) log(x);
% Grado del polinomio
n=2;
% Nodos: 0.9, 1, 1.1
x=[0.9 1 1.1]';fx=f(x);
A=[x ones(n+1,1)];t=x;
for k=1:n-1
t=t.*x;
A=[t A];
end
p=A\fx
% El valor de la aproximación en los puntos pedidos
valor1=polyval(p,0.95678)
valor2=polyval(p,1.03597)
%Las diferencias con los valores que da Matlab es
log(0.95678)-valor1 %1.218237642829495e-04
log(1.03597)-valor2 %-1.022619105114989e-04
% Comprobación
polyval(p,x)-f(x)
% Cota de error
q=poly(x);dq=polyder(q);r=roots(dq);
v=polyval(q,r);M=max(abs(v))
% Derivada tercera de f: 2/x^3 el máximo es 2/(0.9^3)
% El error es M*2/(6*0.9^2)
error=M/(3*0.9^3)
% 1.759945950892248e-04
La elección de nodos que permite minimizar el valor de la expresión,
\[\mathop {\max }\limits_{x \in \left[ {a,b} \right]} \left| {\prod\limits_{j = 0}^n {\left( {x - {x_j}} \right)} } \right|\]que aparece en la
cota de error de interpolación de Lagrange, son los  Pafnuti
Lvóvich Tchebyschev (1821 - 1894). El más prominente miembro de la escuela de matemáticas de St.
Petersburg. Hizo investigaciones en Mecanismos, Teoría de la Aproximación de Funciones, Teoría
de Números y Teoría de Probabilidades. Sin embargo, escribió acerca
de muchos otros temas: formas cuadráticas, construcción de mapas, cálculo geométrico de
volúmenes, etc..
Pafnuti
Lvóvich Tchebyschev (1821 - 1894). El más prominente miembro de la escuela de matemáticas de St.
Petersburg. Hizo investigaciones en Mecanismos, Teoría de la Aproximación de Funciones, Teoría
de Números y Teoría de Probabilidades. Sin embargo, escribió acerca
de muchos otros temas: formas cuadráticas, construcción de mapas, cálculo geométrico de
volúmenes, etc..
Estos nodos en [0, 1] son las raíces del $n+1$-ésimo
Se puede demostrar que
$${T_{n + 1}}(x) = \cos \left( {\left( {n + 1} \right)arc\cos \left( x \right)} \right)\,$$
n=8;a=-3;b=3;
%Para obtener los nodos en un vector
x=(a+b)/2+(b-a)/2*cos((2*(0:n)+1)*pi/(2*n+2));
plot(x,zeros(n+1),'o')
En la siguiente figura se muestran la distribución de los nodos de Chebyshev y se observa que no están igualmente distribuidos en el intervalo $[-3,3]$, se concentran más en los extremos.
Se presenta seguidamente, cuál sería la cota del error si en la interpolación de Lagrange se consideran los nodos de Chevyshev.
Representa la función y los dos polinomios obtenidos.
n=20;% Número de nodos
f=@(x) 1./(1+25*x.^2);
u=linspace(-1,1);
plot(u,f(u))
%polinomio
x=linspace(-1,1,n)'
b=f(x)
m=n-1;
A=x.^(m:-1:0)
p=A\b
hold on
plot(u,polyval(p,u))
hold off
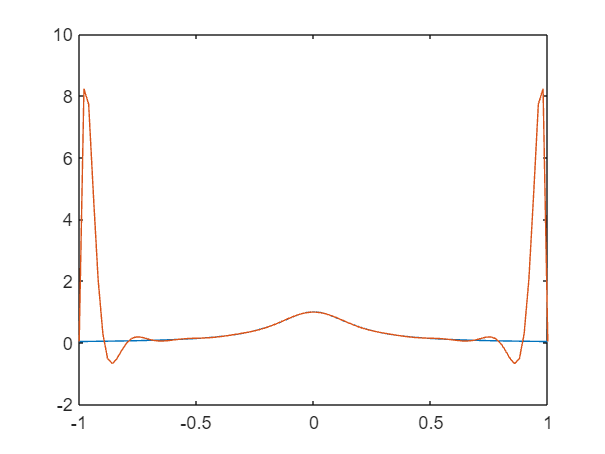
n=20;%Grado polinomio
f=@(x) 1./(1+25*x.^2);
x=linspace(-1,1);
plot(x,f(x))
%Nodos
x=cos((2*(0:n)+1)*pi/(2*n+2))';%21 nodos
%polinomio
b=f(x)
A=x.^(n:-1:0)
p=A\b
hold on
plot(x,polyval(p,x))
hold off
El método de diferencias divididas de Newton es una técnica que permite construir el polinomio de interpolación de forma incremental, se evita recalcular desde cero cuando se añade un nuevo nodo. Gracias a su estructura recursiva, solo es necesario actualizar los términos nuevos, lo que facilita su aplicación en problemas donde se agregan puntos progresivamente.
A partir de los datos, $\{x_0, x_1,...,x_n\}$, se construye una tabla de diferencias divididas:
El polinomio interpolador en forma de Newton se escribe de la forma siguiente:
$$\begin{align*} P(x) &= f[x_0] \\ &\quad+ f[x_0,x_1]\,(x - x_0) \\ &\quad+ f[x_0,x_1,x_2]\,(x - x_0)(x - x_1) \\ &\quad\;\vdots \\ &\quad+ f[x_0,x_1,\dots,x_n]\prod_{i=0}^{n-1}(x - x_i). \end{align*}$$La tabla de diferencias divididas a partir de los datos del problema será:
| $\Delta_1$ | $\Delta_2$ | ||
|---|---|---|---|
| $x_i$ | $f[x_i] = y_i$ | $f[x_i,x_{i+1}]$ | $f[x_i,x_{i+1},x_{i+2}]$ |
| 1 | 3 | $\frac{5 − 3}{2 − 1} = 2$ | $\frac{–1.5 − 2}{4 − 1} = –7/6$ |
| 2 | 5 | $\frac{2 − 5}{4 − 2} = −1.5$ | |
| 4 | 2 | — |
De la tabla se obtiene:
Por tanto, el polinomio de interpolación es:
$$P(x) = 3 + 2·(x − 1) − \frac{7}{6} (x − 1)(x − 2) =$$ $$ = −\frac{7}{6} x²+ \frac{11}{2} x− \frac{4}{3}$$Se puede comprobar que $P(1)=3$, $P(2)=5$ y $P(4)=2$.
Los polinomios de Hermite extienden la interpolación de Lagrange al incluir no solo los valores de la función en ciertos puntos, sino también sus derivadas. Aseguran que la interpolación no solo pase por los puntos dados, sino que también respete las derivadas en esos puntos.
En el siguiente video se muestra un ejemplo de interpolación de Hermite.
Determina el polinomio sin utilizar Matlab/Octave.
Dado que se deben cumplir cuatro condiciones, el polinomio será de grado 3, de la forma:
\[p\left( x \right) = {a_3}{x^3} + {a_2}{x^2} + {a_1}x + {a_o}\]y su derivada es
$$p'\left( x \right) = 3{a_3}{x^2} + 2{a_2}x + {a_1}$$Se buscan los coeficientes cumpliendo el siguiente sistema de ecuaciones:
$$\begin{array}{l}p\left( 0 \right) = {a_3}{0^3} + {a_2}{0^2} + {a_1}0 + {a_o} = 1\\p\left( 1 \right) = {a_3}{1^3} + {a_2}{1^2} + {a_1}1 + {a_o} = 2\\p'\left( 0 \right) = 3{a_3}{0^2} + 2{a_2}0 + {a_1} = 1\\p'\left( 1 \right) = 3{a_3}{1^2} + 2{a_2}1 + {a_1} = 3\end{array}$$Entonces, el sistema a resolver para obtener los coeficientes del polinomio es,
$$\begin{array}{l}{a_o} = 1\\{a_3} + {a_2} + {a_1} + {a_o} = 2\\{a_1} = 1\\3{a_3} + 2{a_2} + {a_1} = 3\end{array}$$Resolviendo el sistema se obtiene: $a_0=1$, $a_1=1$, $a_2=-2$, $a_3=2$ y el polinomio de Hermite buscado es
$$p\left( x \right) = 2{x^3} -2 x^2 + x + 1$$
Se define la función, su derivada y los nodos del ejemplo.
format long
f=@(x) cos(pi*x/2);
df=@(x) sin(pi*x/2)*pi/2;
d2f=@(x) -cos(pi*x/2)*pi^2/4;
x=[0;1];
El polinomio a encontrar es de grado menor o igual a 4, es decir, de la forma
$$\begin{array}{l}p\left( x \right) = {a_4}{x^4} + {a_3}{x^3} + {a_2}{x^2} + {a_1}x + {a_o}\\p'\left( x \right) = 4{a_4}{x^3} + 3{a_3}{x^2} + 2{a_2}x + {a_1}\\p''\left( x \right) = 12{a_4}{x^2} + 6{a_3}x + 2{a_2}\end{array}$$Se define la matriz del sistema a resolver.
A1=[0 0 0 0 1;1 1 1 1 1];
A2=[0 0 0 1 0;4 3 2 1 0];
A3=[0 0 2 0 0];
A=[A1;A2;A3];
Se resuelve el sistema de ecuaciones asociado.
%El término indendiente es
b=[f(x);df(x);d2f(0)];
p=A\b %p=[3.337095776658726;-3.103395226522557;-1.233700550136170;0;1]
A continuación, se presenta la expresión del error que permite estimar la precisión de la interpolación de Hermite.
Se define la función, su derivada y los nodos del ejemplo.
format long
f=@(x) exp(x/2);
df=@(x) exp(x/2)/2
x=[0;pi/2;pi];
El grado del polinomio a calcular es de grado menor o igual a 5. Se considera el término independiente del sistema a resolver.
dx=[f(x);df(x)]
Se escribe en Matlab/Octave la matriz del sistema de ecuaciones a resolver.
A=[x ones(3,1)];t=x;
for k=1:4
t=t.*x;A=[t A];
end
A
B=[2*x ones(3,1) zeros(3,1)];t=x;
for k=3:5
t=t.*x;B=[k*t B];
end
B
Otra forma de generar la matriz podría ser con el siguiente código
A=x.^(5:-1:0);
B=(5:-1:0).*x.^[4:-1:0 0];
Los coeficientes del polinomio se obtienen resolviendo un sistema de ecuaciones.
p=[A;B]\dx
%Comprobación
polyval(p,x)-f(x)
dp=polyder(p);polyval(dp,x)-df(x)
Se calcula una cota del error de la aproximación.
q=poly(x);q=conv(q,q);
dq=polyder(q);r=roots(dq);
v=polyval(q,r);
M=max(abs(v));
error=M*exp(pi/2)/((2^6)*factorial(6))
Se define la función y los nodos y luego se establece la matriz del sistema.
format long
f=@(x) log(1+x);df=@(x) 1./(1+x);
x=linspace(0,1,6)';
El polinomio a determinar es de grado menor o igual que 11 ya que se tienen 12 condiciones. Sus coeficientes serán la solución del sistema de ecuaciones cuya matriz y término independiente son los siguientes:
A1=x.^(11:-1:0);
A2=(11:-1:0).*x.^[10:-1:0 0];
A=[A1;A2];b=[f(x);df(x)];
Se resuelve el sistema para obtener los coeficientes del polinomio.
p=A\b
%Comprobación
polyval(p,x)-f(x)
dp=polyder(p);polyval(dp,x)-df(x)
Para calcular la cota del error, se tiene en cuenta que
$$f'\left( x \right) = {\left( {1 + x} \right)^{ - 1}}\,\,\,\,f''\left( x \right) = - {\left( {1 + x} \right)^{ - 2}}\,\,\,\,\,f'''\left( x \right) = 2{\left( {1 + x} \right)^{ - 3}}$$ $${f^{iv}}\left( x \right) = - 3 \cdot 2{\left( {1 + x} \right)^{ - 4}}\,\,\,\,...\,\,{f^{(12}}\left( {x} \right) = 11!{\left( {1 + x} \right)^{ - 11}}$$Se calcula una cota del error de la aproximación, aplicando la expresión vista y teniendo en cuenta que el máximo de la derivada en $[0,1]$ es $11!$.
$$\left| {f\left( x \right) - p\left( x \right)} \right| \le \frac{{\max \left| {{f^{(12}}\left( x \right)} \right|}}{{12!}}\left| {\prod\limits_{i = 0}^n {{{\left( {x - \frac{i}{5}} \right)}^2}} } \right|$$ $$ \le \frac{{11!}}{{12!}}\left| {{x^2}{{\left( {x - \frac{1}{5}} \right)}^2}{{\left( {x - \frac{2}{5}} \right)}^2}{{\left( {x - \frac{3}{5}} \right)}^2}{{\left( {x - \frac{4}{5}} \right)}^2}{{\left( {x - 1} \right)}^2}} \right|$$
q=poly(x);q=conv(q,q);
dq=polyder(q);r=roots(dq);
v=polyval(q,r);
M=max(abs(v));
%La cota de la derivada dividido el factorial de 12
%es 1/12
error=M/12
En los métodos de interpolación, aumentar el número de puntos no garantiza una mejor aproximación. De hecho, al utilizar un número elevado de nodos, los cálculos pueden volverse computacionalmente costosos y generar errores de redondeo significativos..
Como se verá con el siguiente método, cuando se dispone de abundante información sobre la función en ciertos puntos, en lugar de incrementar notablemente el grado del polinomio interpolador, puede ser más ventajoso emplear el método de mínimos cuadrados.
El siguiente vídeo, junto con la herramienta interactiva, ilustra esta idea aplicando el método al ajuste de una recta.
Como ejemplo, la figura siguiente representa el ajuste de una rectaa los puntos $(-1,3)$, $(2,-1)$, $(3,3)$, $(4,2)$ y $(5,0)$ utilizando el método de mínimos cuadrados.
Considerando los mismos puntos y el ajuste por mínimos cuadrados a un polinomio de grado 2, se obtendría la curva que se muestra en la figura siguiente.
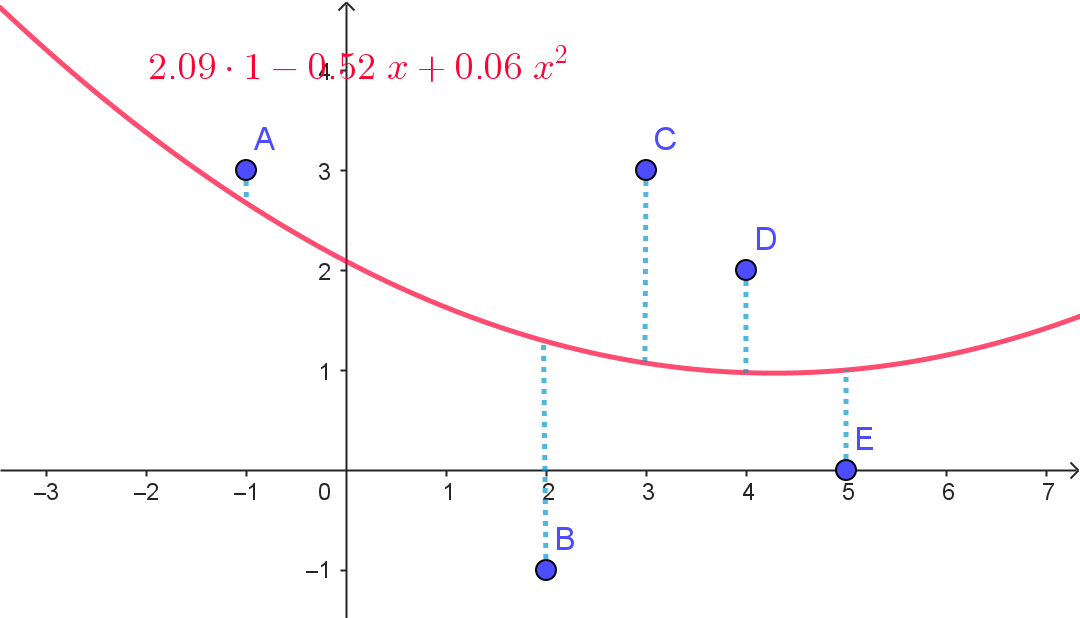
Se describe seguidamente la formulación del método de mínimos cuadrados.
Se muestra cómo se puede formular algebraicamente el problema de encontrar el polinomio $p$ de grado menor o igual a $k$ que minimice la siguiente expresión $$\sum\limits_{j = 0}^n {{\omega _j}} {\left( {p\left( {{x_j}} \right) - f\left( {{x_j}} \right)} \right)^2}$$
Se considera para ello un polinomio $p$ de grado $k$,
$$p\left( x \right) = {a_o} + {a_1}x + {a_2}{x^2} + .. + {a_k}{x^k}$$y las siguientes matrices
Teniendo en cuenta la norma euclídea $${\left\| {Aa - b} \right\|^2} = \sum\limits_{j = 0}^n {{\omega _j}} {\left( {p\left( {{x_j}} \right) - f\left( {{x_j}} \right)} \right)^2}$$ los la solución del problema del problema:
$$\mathop { (P2) \,\,\,\,{\rm{minimizar}}}\limits_{x \in {{\mathbb R}^{k + 1}}} {\left\| {Ax - b} \right\|^2}$$serán los coeficientes del polinomio $p$ que se busca.
Se trata de encontrar por tanto el vector $x$, que se corresponde con los coeficientes del polinomio, que haga mínimo la norma del vector de residuos $Ax-b$, es decir, la desviación global entre la aproximación, $Ax$, y los datos observados $b$.
Se desea determinar L, y al mismo tiempo la constante del muelle usando la ley de Hooke: $F=k(h-L)=kh-kL$ donde $F$ denota la fuerza aplicada al muelle y $h$ es la distancia desde el extremo superior del muelle. Para ello, se disponen de los siguientes datos,
| $h$ | 6 | 7 | 10 |
| $F$ | 3 | 8 | 12 |
Se llama $a_1=k$ y $a_0=-kL$ y se busca la recta $F(h)=a_1h+a_20$ que se ajuste a los datos. El sistema resultante es,
$$ 6{a_1} + {a_0} = 3 $$ $$ 7{a_1} + {a_0} = 8 $$ $$ 10{a_1} + {a_0} = 12 $$En forma matricial, se podría escribir de la forma $Ax=b$ siendo
$$ A= \begin{pmatrix} 6& 1 \\ 7& 1 \\ 10& 1 \\ \end{pmatrix} \,\,\,\,\, x= \begin{pmatrix} a_1 \\ a_0\\ \end{pmatrix}\,\,\,\,\, b= \begin{pmatrix} 3 \\ 8\\ 12\\ \end{pmatrix}$$El problema de mínimos cuadrados consiste en encontrar el vector $x$ de ${\mathbb R}^2$ de forma que sea mínima la expresiónn: $\left\| {Ax - b} \right\|$.
En este apartado se verá cómo resolver el problema siguiente,
$$(P2) \,\,\,\,\,\ \mathop {{\rm{minimizar}}}\limits_{x \in {{\mathbb R}^{k + 1}}} {\rm{ }}{\left\| {Ax - b} \right\|^2}$$utilizando la descomposición QR de la matriz $A$ de orden $(n+1)\text{x}(k+1)$ siendo $k$ el grado del polinomio y $n+1$ el número de puntos. El método se describe a continuación.
A continuación, se justifica el punto 3.
Como Q es ortogonal se cumple
$${\left\| {Qv} \right\|^2} = {\left( {Qv} \right)^T}\left( {Qv} \right) = {v^T}\left( {{Q^T}Q} \right)v = {v^T}Iv = {v^T}v = {\left\| v \right\|^2}$$Por lo tanto, $${\left\| {Ax - b} \right\|^2} = {\left\| {QRx - b} \right\|^2} = {\left\| {Q\left( {Rx - {Q^T}b} \right)} \right\|^2} = $$ $${\left\| {Rx - {Q^T}b} \right\|^2} = {\left\| {\,\left( {_O^{\widehat R}} \right)x - \left( {_{{Z^T}}^{{Y^T}}} \right)b\,} \right\|^2} = {\left\| {\,\left( {_{ - {Z^T}b}^{\widehat Rx - {Y^T}b}} \right)\,} \right\|^2} = $$ $${\left\| {\,\widehat Rx - {Y^T}b\,} \right\|^2} + {\left\| {\,{Z^T}b\,} \right\|^2}$$
El mínimo valor del problema se obtiene para el valor de $x$ que hace cero el término $${\left\| {\,\widehat Rx - {Y^T}b\,} \right\|^2}$$
De la expresión anterior se deduce que la solución del problema $(P_2)$ se obtiene de forma equivalente calculando el valor $x$ solución del sistema $${\widehat Rx = {Y^T}b}$$
donde si $k$ es el grado del polinomio buscado y $QR$ es la factorización de $A$, la matriz $\widehat R$ es la submatriz de $R$ con las primeras $k+1$ filas y la matriz $Y$ es la submatriz de $Q$ considerando las primeras $k+1$ columnas.| $h$ | 6 | 7 | 10 |
| $F$ | 3 | 8 | 12 |
A partir de los datos, se tiene
$$ A= \begin{pmatrix} 6& 1 \\ 7& 1 \\ 10& 1 \\ \end{pmatrix} \,\,\,\,\, x= \begin{pmatrix} a_1 \\ a_0\\ \end{pmatrix}\,\,\,\,\, b= \begin{pmatrix} 3 \\ 8\\ 12\\ \end{pmatrix}$$ Para encontrar la descomposición $QR$ de la matriz $A$ se puede utilizar el código Matlab siguiente,
[Q,R]=qr([6 1;7 1;10 1])
Como se trata de una recta, el valor de $k$ es 1. Las matrices $Y$, $\widehat R$ son
$$ Y= \begin{pmatrix} -0.4411 & -0.6777 \\ -0.5147 & -0.3460 \\ -0.7352 & 0.6488 \\ \end{pmatrix} \,\,\,\,\, \widehat R= \begin{pmatrix} -13.6015 & -1.6910\\ 0 & -0.3749\\ \end{pmatrix}$$El sistema a resolver es entonces, $\widehat Rx=Y^Tb$.
Es decir,
$$ \begin{pmatrix} -13.6015 & -1.6910\\ 0 & -0.3749\\ \end{pmatrix} \begin{pmatrix} a_1\\ a_0\\ \end{pmatrix} $$ $$ \,\,\,\,\, = \begin{pmatrix} -0.4411 & -0.5147 & -0.7352 \\ -0.6777 & -0.3460 & 0.6488 \\ \end{pmatrix} \begin{pmatrix} 3\\ 8\\ 12\\ \end{pmatrix}$$ Operando, $$ \begin{pmatrix} -13.6015 & -1.6910\\ 0 & -0.3749\\ \end{pmatrix} \begin{pmatrix} a_1\\ a_0\\ \end{pmatrix}=\begin{pmatrix} -14.2632\\ 2.9847\\ \end{pmatrix} $$La solución de este sistema es $a_1=2.0385$ y $a_o=-7.9615$
Las submatrices $Y$ y $\widehat R$ se obtienen a partir de $Q$ y $R$ con el código siguiente.
k=1;
Y=Q(:,1:k+1)'
RG=R(1:k+1,:)
fx=[3;8;12];
p=RG\Y*fx
h=[6;7;10];
ph=polyval(p,h);
plot(h,fx,'o')
hold on
plot(h,ph)
hold off
f=@(x) 1./(1+x.^2);
n=99;k=20;a=-5;b=5;
x=linspace(a,b,n+1)';fx=f(x);
A=[ x ones(n+1,1)];t=x;
for iter=1:k-1
t=t.*x;
A=[t A];
end;
[Q,R]=qr(A);
p=R(1:k+1,:)\Q(:,1:k+1)'*fx;
%Representamos la función
s=linspace(a,b,1001)';
fs=f(s);ps=polyval(p,s);
plot(s,[ps fs])
| T (K) | 8 | 10 | 12 | 14 | 16 | 18 |
| C(T) | 0.0236 | 0.0475 | 0.083 | 0.1736 | 0.202 | 0.25 |
Halla el polinomio interpolador y da un valor aproximado del calor específico a 15 K. Representa gráficamente los datos y el polinomio interpolador.
Da una cota del error de interpolación y compara el resultado con el máximo en valor absoluto de la diferencia entre la función y el polinomio tomando 500 puntos del intervalo $[0,1]$.
Dada la función \(f(x) = \sin(\pi x)\), calcula el polinomio de interpolación \(p(x)\) que resuelve los siguientes problemas:
Representa gráficamente ambos polinomios junto con la función \(f(x)\).
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 0.5 | 2.5 | 2 | 4 | 3.5 | 6 | 5.5 |
Determina el polinomio interpolador que se ajusta a estos valores y grafica las soluciones junto con el conjunto \((x, y)\) en la misma figura.
El capítulo también aborda la elección óptima de nodos, como los nodos de Chebyshev, para mejorar la precisión de la interpolación y evitar problemas como el fenómeno de Runge. Además, se discuten las limitaciones de los métodos de interpolación en casos de funciones con comportamientos complejos,
Los aspectos clave estuadiados en este tema son:

Los métodos numéricos de integración sirven para aproximar el valor de una integral definida de una función en un intervalo con una precisión dada cuando no es posible resolverla de forma exacta o analítica. El interés de estas técnicas puede venir motivado por distintas razones.
Estas razones obligan a encontrar métodos alternativos para calcular de forma aproximada el valor de una integral
definida en un intervalo. Por razones históricas, el cálculo aproximado de
integrales se denomina
Se comienza viendo un ejemplo de aplicación. La gestión sostenible del agua, incluida en el ODS 6 Objetivos de Desarrollo Sostenible, requiere controlar el caudal de los ríos para garantizar su uso resposable. Sin embargo, el caudal no siempre se mide directamente en todo el curso del río, sino que se calcula a partir de datos como la velocidad del agua en diferentes puntos y las características de la sección transversal del río.
Para calcular el caudal específico de agua que pasa por una sección transversal del río, se debe integrar la velocidad del agua a lo largo de la profundidad del río, obteniendo el volumen que pasa por cada metro de ancho del cauce. La fórmula para ello es la siguiente,
$$Q = \int\limits_a^b {v\left( x \right)dx} $$donde $Q$ es el caudal específico, $v(x)$ es la velocidad del agua en el punto $x$ de la seccion transversal y $a$ y $b$ son los límites de la sección transversal. En la siguiente tabla se recogen unos datos para calcular el valor aproximado de $Q$ con alguna técnica que se mostrará en este capítulo.
| Profundidad (m) | Velocidad (m/s) |
|---|---|
| 0 | 0.0 |
| 1 | 1.2 |
| 2 | 2.1 |
| 3 | 2.4 |
| 4 | 2.0 |
| 5 | 1.5 |
| 6 | 0.0 |
La figura 5.1 muestra la velocidad del agua en función de la profundidad. El área bajo la curva es el valor a calcular.
Si se utiliza por ejemplo la fórmulas de cuadratura compuesta de los trapecios, que se verá en este tema, se podría obtener un valor aproximado del caudal o volumen que fluye, $Q$, de la forma siguiente,
\[ Q \approx \frac{h}{2} \left[v(x_0) + 2 \sum_{i=1}^{5} v(x_i) + v(x_6)\right] \approx 9.2\]
donde:
Así, si $p(x)$ es un polinomio interpolador de $f$ en $n+1$ nodos,
$$\left\{ {{x_i}} \right\}_{i = 0}^n \subset \left[ {a,b} \right]\,\,\,\,\,\,\,\,\,\,\,\,p\left( {{x_i}} \right) = f\left( {{x_i}} \right)\,\,i = 0,1,...,n$$una aproximación del valor de la integral de $f$ en $[a,b]$ será:
$$\int\limits_a^b {f\left( x \right)dx} \approx \int\limits_a^b {p\left( x \right)dx} $$
se obtendría, $$\int\limits_a^b {p\left( x \right)dx} = \sum\limits_{i = 0}^n {f\left( {{x_i}} \right)\int\limits_a^b {{l_i}\left( x \right)dx} } = $$ $$ = \left( {b - a} \right)\sum\limits_{i = 0}^n {f\left( {{x_i}} \right)\underbrace {\left( {{1 \over {b - a}}\int\limits_a^b {{l_i}\left( x \right)dx} } \right)}_{{w_i}}} $$
Si fuera de tipo interpolatorio, se tendría que cumplir $\omega_0=3/2$ pero
$$\omega_0={\frac{1}{2}}\int\limits_0^2 {{l_o}\left( x \right)dx} = {\frac{1}{2}} \int\limits_0^2 {{{x - {x_1}} \over {{x_o} - {x_1}}}\,} dx = {\frac{1}{2}} \int\limits_0^2 {{{x - 2} \over {0 - 2}}\,} dx = {\frac{1}{2}} \ne {\frac{3}{2}} $$ Por lo tanto, la fórmula no es de tipo interpolatorio.De cara a obtener los pesos, resulta de utilidad el resultado siguiente.
Este resultado significa que si se cambia de intervalo $[a,b]$ a $[c,d]$ y se consideran los nodos $x_i$ en $[a,b]$ y $t_i$ en $[c,d]$ relacionados de la forma siguiente: $${t_i} = c + {{d - c} \over {b - a}}\left( {{x_i} - a} \right)$$ se tendrá que los pesos de la fórmula interpolatoria en ambos casos coinciden.
En el siguiente interactivo se muestra dos intervalos, $[a,b]$ y $[c,d]$ y cómo está vinculado el punto $x$ en $[a,b]$, en rojo, con el correspondiente punto $t$ en $[c,d]$ que se muestra en naranja considerando la correspondencia anterior.
Para calcular la calidad de una fórmula de cuadratura se define su grado de precisión o exactitud.
Por lo que su grado de precisión es exactamente uno.
Se analizará en este apartado las
Para obtener el valor de los pesos se puede considerar por ejemplo el intervalo $[0,3]$ y los nodos $x_0=0$, $x_1=1$, $x_2=2$ y $x_3=3$ ya que, como se ha visto anteriormente, el valor de los pesos es el mismo siempre que en un intervalo se consideren como se indicaba para $[a,b]$.
Resolviendo el sistema, se obtiene $\omega_0=1/8$, $\omega_1=3/8$, $\omega_2=3/8$ y $\omega_3=1/8$. El siguiente código Matlab/Octave permite resolver el sistema.
x=[0 1 2 3];
format rational
A=x.^[0;1;2;3];
%También x.^([0:3]')
b=[1;3/2;3;27/4];
pesos=A\b
Se muestra a continuación las primeras fórmulas de Newton-Cotes tomando diferentes números de nodos $x_0$, $x_1$, ..., $x_n$. Para ello, se utilizará que el cálculo de los pesos no depende del intervalo considerado siempre que se tomen los nodos equidistantes en dicho intervalo y se consideren los extremos del intervalo de integración.
En este caso se considerarán dos nodos en el intervalo $[a,b]$, esto es, $x_0=a$ y $x_1=b$. La fórmula de cuadratura será de la forma, $$\int\limits_a^b {f\left( x \right)dx} \approx \left( {b - a} \right)\left[ {{\color{red}{{\omega _o}}}f\left( a \right) + {\color{red}{{\omega _1}}}f\left( b \right)} \right]$$
Para calcular los nodos se puede tomar por ejemplo $[a,b]=[0,1]$ y aplicar que la fórmula de cuadratura es exacta al menos de grado $n=1$, es decir, es exacta para $f(x)=1$ y para $f(x)=x$. Resolviendo el sistema 2x2, se obtiene ${\omega _o} = {\omega _1} = {1 \over 2}$.
Observad que el polinomio interpolador que pasa por dos puntos es la recta que pasa por dichos puntos, de ahí el nombre de la fórmula de cuadratura.

En la siguiente escena interactiva, se muestra la aproximación que da la regla de los trapecios, según la función y el intervalo que se introduzca como datos.
En este caso, el número de nodos equidistantes en $[a,b]$ es 3, y sérán los puntos siguientes: $x_o=a$, $x_1=\frac{a+b}{2}$ y $x_2=b$ y la fórmula de
cuadratura es
$$\int\limits_a^b {f\left( x \right)dx} \approx \left( {b - a} \right)\left[
{{\color {red}{\omega _o}}f\left( a \right) +{\color{red} {\omega _1}}f\left( {{{a + b} \over 2}} \right) + {\color{red}{\omega
_2}}f\left( b \right)} \right]$$
Para determinar los nodos, se puede considerar el intervalo $[a,b]=[-1,1]$ y resolver el sistema de 3 ecuaciones con tres incógnitas que resulta de aplicar que la fórmula de cuadratura es exacta para $f(x)=1$, $f(x)=x$ y $f(x)=x^2$.
Los valores de los pesos obtenidos serían ${\omega _o} = {\omega _2} = {1 \over 6}$, ${\omega _1} = {2 \over 3}$.
En la siguiente escena interactiva se puede analizar las aproximaciones de la cuadratura introduciendo la función y el intervalo. Se puede ver que la aproximación es mejor cuanto menor es la longitud del intervalo.
En este caso el número de nodos equidistantes que se considera en el intervalo $[a,b]$ es 4: $x_0=a$, $x_1=a+\frac{b-a}{3}$, $x_2=a+2 \frac{b-a}{3}$ y $x_3=b$ y la fórmula de cuadratura es $$\int\limits_a^b {f\left( x \right)dx} \approx \left( {b - a} \right)\left[ {{\color{red}{{\omega _0}}}f\left( a \right) + {\color{red}{{\omega _1}}}f\left( { {{2a+b} \over 3}} \right) + } \right.{\rm{ }}$$ $$\left. +{{\color{red}{{\omega _2}}}f\left( {{{a+2b} \over 3}} \right) + {\color{red}{{\omega _3}}}f\left( b \right)} \right]$$
Para determinar los nodos se considera el intervalo $[0,3]$ y se resuelve el sistema de 4 ecuaciones con 4 incógnitas asociado, obteniendo ${\omega _o} = {\omega _3} = {1 \over 8}$, ${\omega _1} = {\omega _2} = {3 \over 8}$.
De forma análoga, se pueden obtener las fórmulas de Newton-Cotes cerradas para $n$ desde 1 hasta 6 que se muestran a continuación.
Considerando $f(x)=e^{senx\,\,\cos x}$, el valor que aproxima a la integral es $$\int\limits_0^\pi {{e^{senx\cos x}}dx} \approx \frac{\pi }{8}\left( {f\left( 0 \right) + 3f\left( {\frac{\pi }{3}} \right) + 3f\left( {\frac{{2\pi }}{3}} \right) + f\left( \pi \right)} \right)$$
format long
f=@(x) exp(sin(x).*cos(x));
a=0;b=pi;
%Regla tres octavos
h=(b-a)/3;nodos=a:h:b
coef=[1 3 3 1];
valor=sum(f(nodos).*coef)*(b-a)/8 %3.365958987799939
function valor=TresOctavos(f,a,b)
h=(b-a)/3;
nodos=a:h:b
coef=[1 3 3 1];
valor=sum(f(nodos).*coef)*(b-a)/8;
end
Para llamar a la función, se utilizará el siguiente código,
fun=@(x) exp(sin(x).*cos(x));
aprox=TresOctavos(fun,0,pi)
En este apartado se analizará el error de la aproximación, es decir, la diferencia entre el valor exacto dado por la integral y el valor aproximado que se obtiene con la fórmula de Newton-Cotes $$E = \int\limits_a^b {f\left( x \right)dx} - \left( {b - a} \right)\sum\limits_{j = 0}^n {{\omega _j}f\left( {{x_j}} \right)} $$
A continuación se presenta la expresión del término del resto para algunas de las fórmulas cerradas de Newton-Cotes vistas en el apartado anterior, considerando $h=\frac{b-a}{n}$. Algunas de estas expresiones del resto se demostrarán en el apartado siguiente.
Las derivadas de $f$ son
$$f'\left( x \right) = \cos \left( x \right){e^{sen\left( x \right)}}{\rm{ }}$$$$ f''\left( x \right) = {\cos ^2}\left( x \right){e^{sen\left( x \right)}} - sen\left( x \right){e^{sen\left( x \right)}}$$Por lo tanto, una cota sencilla de calcular de la derivada segunda podría ser: $\left| {f''\left( x \right)} \right| \le 2e$. Utilizando la expresión del error, una cota de la aproximación será entonces,
$$\left| E \right| = \left| { - {{{\pi ^3}} \over {96}}{f^{''}}\left( \xi \right)} \right| \le {{{\pi ^3}e} \over 48}\approx 0.642$$La cota obtenida es muy grande, por lo que no permite determinar la bondad de la aproximación. Matlab/Octave da como aproximación utilizando el comando integral el valor $3.104379017855555$.
Se tiene $f(x)={\log \left( {1 + {e^x}} \right)}$, $a=0$ y $b=1$. Dado que $$f'\left( x \right) = \frac{{{e^x}}}{{1 + {e^x}}}$$ $$f''\left( x \right) = \frac{{{e^x}\left( {1 + {e^x}} \right) - {e^x}{e^x}}}{{{{\left( {1 + {e^x}} \right)}^2}}} = \frac{{{e^x}}}{{{{\left( {1 + {e^x}} \right)}^2}}}$$
Teniendo en cuenta que la derivada segunda tiene un máximo en el punto 0, una cota del error podría ser
$$\left| { - \frac{{{h^3}}}{{12}}f''\left( \xi \right)} \right| \le \frac{1}{{12 \cdot 4}}\,\,\,\,\,\,\,\,\,\,\,\,\xi \in \left[ {0,1} \right]$$Este valor es aproximadamente $0.0208$. El valor de la aproximación sería:
$$\int\limits_0^1 {\log \left( {1 + {e^x}} \right)dx} \approx \frac{1}{2}\left( {f\left( 0 \right) + f\left( 1 \right)} \right) = \frac{{\log 2 + \log \left( {1 + e} \right)}}{2} \approx {\rm{1}}{\rm{.0032}}$$El valor que devuelve Matlab/Octave como aproximación utilizando el comando integrales $0.983819037020661$.
La expresión del error se puede escribir de la siguiente manera;
$$E = \left\{ \begin{aligned} &{C_n}{h^{n + 2}}{f^{(n + 1}}\left( \xi \right)\,\,\,\,\,\text{si n impar} \\ &{C_n}{h^{n + 3}}{f^{(n + 2}}\left( \xi \right)\,\,\,\,\,\text{si\ n par} \end{aligned} \right. $$donde la constante $C_n$ tiene el siguiente valor:
$$C_n = \left\{ \begin{aligned} &{1 \over {\left( {n + 1} \right)!}}\int\limits_0^n {t \left( {t - 1} \right)\left( {t - 2} \right)} ...\left( {t - n} \right)dt \,\,\,\,\,\text{si n impar} \\ & {1 \over {\left( {n + 2} \right)!}}\int\limits_0^n {t^2 \left( {t - 1} \right)\left( {t - 2} \right)} ...\left( {t - n} \right)dt \,\,\,\,\,\text{si n par} \end{aligned} \right. $$Se determinará seguidamente el valor de las constantes $C_n$ para las primeras fórmulas de Newton-Cotes.
Se considera la fórmula de Newton-Cotes para $n=1$, que es impar. Se toma $m=n+1=2$. Se tiene que $$\begin{aligned} E=&\color{red}{\int\limits_a^b {f\left( x \right)dx}} \color{black}{-} \color{green}{{{b - a} \over 2}\left( {f\left( a \right) + f\left( b \right)} \right)} \\ E=&{C_1} h^3 f''\left( \xi \right) \end{aligned}$$
Para determinar $C_1$, se considera la función $f(x)=(x-a)^m=(x-a)^2$.
Para esta función se tiene que por un lado se cumple
$$\color{red}{\int\limits_a^b {f(x)dx}} \color{black}{=\int\limits_a^b {{(x-a)^2}dx} = {1 \over 3}{\left( {b - a} \right)^3} =} \color{red}{{ {h^3} \over 3}}$$y por otro
$$\color{green}{{{b - a} \over 2}\left( {f\left( a \right) + f\left( b \right)} \right)} \color{black}{= {{b - a} \over 2}\left( {0 + {{\left( {b - a} \right)}^2}} \right) =} {{{{\left( {b - a} \right)}^3}} \over 2} = \color{green}{ \frac {h^3} {2}}$$Por lo tanto,
$${C_1}{h^3}{f^{''}}\left( \xi \right) = {\color{red}{{{h^3}} \over 3}} -\color{green} {{h^3} \over 2}$$como ${f^{''}}\left( \xi \right)=2$, se tiene,
$$2 {C_1} = {1 \over 3} - {1 \over 2} = - {1 \over 6}$$ $${C_1} = - {1 \over 12}$$Se considera la fórmula de Newton-Cotes para $n=2$ que es par, se toma $m=n+2=4$. Se tiene que $$\begin{aligned} E=&\int\limits_a^b {f\left( x \right)dx} - {{{b - a} \over 6}\left[ {f\left( a \right) + 4f\left( {{{a + b} \over 2}} \right) + f\left( b \right)} \right]} \\ E=&{C_2} h^5 f''\left( \xi \right) \end{aligned}$$ Para determinar $C_2$ se considera la función $f(x)=(x-a)^m=(x-a)^4 $. Se tiene que por un lado se cumple $$\int\limits_a^b {{(x-a)^4}dx} = {1 \over 5}{\left( {b - a} \right)^5} = { {(2h)^5} \over 5}$$ y por otro $${{b - a} \over 6}\left[ {0 + 4\, \cdot {h^4} + {(2h)^4}} \right] = {{2h^5} \over 6} \cdot 20$$
Por lo tanto, $${C_2}{h^5}{f^{iv}}\left( \xi \right) = {{{2^5 h^5}} \over 5} - {{20 h^5} \over 3}$$ es decir, $$4!{C_2} = {{{2^5}} \over 5} - {{20} \over 3} = - {4 \over {15}}\,\,\,\,\,\,\, \Rightarrow \,\,\,\,\,\,{C_2} = - {1 \over {90}}$$Se considera la fórmula de Newton-Cotes para $n=3$, que es impar y se toma $m=n+1=4$. Se tiene que $$E=\int\limits_a^b {f\left( x \right)dx} - $$ $${{\left( {b - a} \right)} \over 8}\left[ {f\left( a \right) + 3f\left( {{{2a + b} \over 3}} \right) + 3f\left( {{{a + 2b} \over 3}} \right) + f\left( b \right)} \right] $$
$$E={C_3} h^5 f^{(4}\left( \xi \right)$$Para determinar $C_3$ se considera la función $f(x)=(x-a)^m=(x-a)^4$. Se cumplirá $$\int\limits_a^b {{(x-a)^4}dx} = {1 \over 5}{\left( {b - a} \right)^5} = { {(3h)^5} \over 5}$$ $${{3h} \over 8}\left[ 0 + 3\, \cdot {h^4} + 3\, \cdot (2h)^4 + (3h)^4 \right] = {{99h^5} \over 2} $$ Por lo tanto, $$E={C_3} h^5 f^{(4}\left( \xi \right)=\frac{-9}{10}h^5$$ $$4!{C_3} = {{ - 9} \over {10}}\,\,\,\,\,\, \Rightarrow \,\,\,{C_3} = - {3 \over {80}}$$
Cuando la distancia entre los nodos aumenta, el error que se comete, de forma general, también aumenta considerablemente. Para conseguir una mejor aproximación, se puede dividir el intervalo $[a,b]$ en $N$ subintervalos y utilizar una fórmula de cuadratura en cada uno de los subintervalos. Por linealidad de la integral, se tendrá
$$a = {\alpha _o} < {\alpha _1} < ... < {\alpha _N} = b \,\,\,\,\,,\,\,\,\,\,\,\int\limits_a^b {f\left( x \right)dx} = \sum\limits_{i = 1}^N {\int\limits_{{\alpha _{i - 1}}}^{{\alpha _i}} {f\left( x \right)dx} } $$La aproximación de las fórmulas compuestas consiste en aplicar una fórmula de cuadratura en cada subintervalo $[{\alpha _{i-1}},{\alpha _i}]$.
En este caso, la fórmula quedaría de la forma siguiente, teniendo en cuenta que la longitud de cada subintervalo es $\frac{b-a}{N}$.
$$\int\limits_a^b {f\left( x \right)dx} \approx \frac{{\left( {b - a} \right)}}{{2N}}\sum\limits_{i = 1}^N {\left[ {f\left( {{\alpha _{i - 1}}} \right) + f\left( {{\alpha _i}} \right)} \right]} $$
La
Se define una función que calcule la regla de los trapecios compuesta.
function valor=TrapecioCompuesta1(f,a,b,N)
%Aproxima la integral de f en el intervalo [a,b]
h = (b-a)/N;x=linspace(a,b,N+1);I = 0;
for k = [1:N]
I = I + f(x(k))+f(x(k+1));
end
valor=I*h/2;
end
También se podría escribir esta función de la forma siguiente.
function valor = TrapecioCompuesta(f, a, b, N)
%Aproxima la integral de f en el intervalo [a,b]
%usando la regla compuesta de los trapecios
h = (b-a)/N;x=linspace(a,b,N+1); %Tambien: x=a:h:b;
valor = h/2*(f(a)+f(b))+h*sum(f(x(2:end-1)));
end
Para utilizar la función y calcular de forma aproximada la integral pedida:
f=@(x) sqrt(x).*log(sin(x))
%Regla compuesta de los trapecios con N=5
TrapecioCompuesta(f,1,pi/2,5)
%-0.034825244439641
%Con comando integral Matlab: -0.034221721637133
Una cota del error en la aproximación utilizando la regla compuesta del trapecio considerando $N$ subintervalos será
$${{M \cdot N} \over {12}}{\left( {{{b - a} \over N}} \right)^3} = {{M{{(b - a)}^3}} \over {12{N^2}}}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} con{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} M = \mathop {\max }\limits_{c \in \left( {a,b} \right)} \left| {f''\left( c \right)} \right|$$Teniendo en cuenta que,
$$f'\left( x \right) = - {e^{senx}}\cos x$$ $$f''\left( x \right) = {e^{senx}}{\cos ^2}x - {e^{senx}}senx$$aplicando la desigualdad triangular y que el seno y coseno toman como máximo el valor 1, se tiene $M \le 2e$. Una cota del error de aproximación será entonces
$$\ \frac{{{\pi ^3}}}{{12 \cdot {8^2}}}2e\, \approx {\rm{0}}{\rm{.2194}}$$El valor aproximado de la integral sería:
$$\int\limits_0^\pi {{e^{senx}}} dx \approx \frac{\pi }{{16}}\left[ {f\left( 0 \right) + 2f\left( h \right) + ... + 2f\left( {\pi - h} \right) + f\left( \pi \right)} \right]$$tomando $h=\pi/8$. Para realizar el cálculo, el código Matlab/Octave a utilizar es el siguiente.
f=@(x) exp(sin(x));
%Regla compuesta de los trapecios con N=8
valor=TrapecioCompuesta(f,0,pi,8)
%6.183057933280413
%Con comando integral Matlab: 6.208758035711110
Apartado a) Si se llama $M$ a la cota de la derivada segunda de $f(x)=e^{x^2}$ en el intervalo $[0,2]$, lo que nos piden es encontrar $N$ de forma que $$ \frac{{{{\left( {b - a} \right)}^3}}}{{12{N^2}}}M \le 10^{-4}$$
Esto es
$$\frac{{{{\left( {b - a} \right)}^3}}}{{12 \cdot {{10}^{ - 4}}^{}}}M \le {N^2} \Leftrightarrow N \ge \sqrt {\frac{{{{\left( {b - a} \right)}^3}}}{{12 \cdot {{10}^{ - 4}}^{}}}M} $$Se tiene $a=0$, $b=2$ y $M=18e^4$ ya que
$$\begin{array}{l}f'\left( x \right) = 2x{e^{{x^2}}}\\f''\left( x \right) = 2{e^{{x^2}}} + 4{x^2}{e^{{x^2}}} = \left( {2 + 4{x^2}} \right){e^{x^2}}\end{array}$$Para conseguir el error pedido, bastaría tomar tomar $N=2560$ y el valor de la integral sería:
f=@(x) exp(x.^2);
%Regla compuesta de los trapecios con N=2560
valor=TrapecioCompuesta(f,0,2,2560)
%16.452638873526805
%Con comando integral Matlab: 16.452627765507231
Apartado b). Si se llama $M$ a la cota de la derivada segunda de $f(x)=cos(\pi x^2)$ en el intervalo $[0,1]$, lo que nos piden es encontrar $N$ de forma que $$\frac{{{{\left( {b - a} \right)}^3}}}{{12{N^2}}}M \le {10^{ - 4}}$$
Se tiene $a=0$, $b=1$ y $M=2\pi+4\pi^2$ ya que
$$\begin{array}{l}f'\left( x \right) = sen\left( {\pi {x^2}} \right)2\pi x\\f''\left( x \right) = - \cos \left( {\pi {x^2}} \right){\left( {2\pi x} \right)^2} + sen\left( {\pi {x^2}} \right)2\pi \end{array}$$Luego,
$$N \ge \sqrt {\frac{{{1^3}}}{{12 \cdot {{10}^{ - 4}}^{}}}\left( {2\pi + 4{\pi ^2}} \right)} \approx 195.28$$Por lo tanto, se puede tomar $N=196$ para obtener la aproximación con el error dado.
f=@(x) cos(pi*x.^2);
%Regla compuesta de los trapecios con N=196
valor=TrapecioCompuesta(f,0,1,196) %0.373982833304262
%Con comando integral Matlab: 0.373982833415732
En este caso, si se divide el intervalo en $N$ subintervalos y se aplica la regla de Simpson compuesta a cada uno de ellos, se tendrá:
$$\int\limits_a^b {f\left( x \right)dx} = \sum\limits_{i = 1}^N {\left( {\int\limits_{{\alpha _{i - 1}}}^{{\alpha _i}} {f\left( x \right)dx} } \right)} $$ $$ \approx \sum\limits_{i = 1}^N {\left( \frac{{\left( {b - a} \right)}}{{6N}}\left[ {f\left( {{\alpha _{i - 1}}} \right) + 4f\left( {\frac{{{\alpha _{i-1}} + {\alpha _i}}}{2}} \right) + f\left( {{\alpha _i}} \right)} \right] \right)} $$
La
Se define una función que calcule la regla de los trapecios compuesta.
function valor = SimpsonCompuesta(f, a, b, N)
%Aproxima la integral de f en el intervalo [a,b]
h=(b-a)/N;
x=linspace(a,b,2*N+1); %También x=a:h/2:b
valor=(h/6)* (f(x(1))+ 2*sum(f(x(3:2:end-2)))+ 4*sum(f(x(2:2:end)))+f(x(end)))
end
Para utilizar la función y calcular de forma aproximada la integral pedida
f=@(x) sqrt(x).*log(sin(x))
%Regla compuesta de los trapecios con N=10
SimpsonCompuesta(f,1,pi/2,5) %-0.034221742037540
%Con comando integral Matlab: -0.034221721637133
| r (pies) | 0.308 | 0.325 | 0.342 | 0.359 | 0.376 | 0.393 | 0.410 | 0.427 | 0.444 | 0.461 | 0.478 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| T(r) (°F) | 640 | 794 | 885 | 943 | 1034 | 1064 | 1114 | 1152 | 1204 | 1222 | 1239 |
r=[0.308 0.325 0.342 0.359 0.376 0.393 0.410 0.427 0.444 0.461 0.478];
T=[640 794 885 943 1034 1064 1114 1152 1204 1222 1239]
%El número de subintervalos es N=5
%El número de nodos es 11=2*N+1 con N=5 subintervalos
%Aplicando la fórmula de Simpson compuesta se
%obtienen los siguientes valores
a=0.308;b=0.478;N=5;h=(b-a)/N;%Longitud de cada intervalo
%donde se aplica Simpson
f=0.7051*T.*r;
I1=(h/6)* (f(1)+ 2*sum(f(3:2:end-2))+ 4*sum(f(2:2:end))+f(end));
g=0.7051*r;
I2=(h/6)* (g(1)+ 2*sum(g(3:2:end-2))+ 4*sum(g(2:2:end))+f(end));
%El valor de la temperatura es
T=I1/I2 %20.602700006958784
Si se considera $M$ el máximo del valor absoluto de la derivada cuarta de la función en el intervalo $(a,b)$, una cota del error en la fórmula de cuadratura de Simpson considerando $N$ subintervalos es,
\[\left| E \right|\le \frac{N\cdot M}{90}{{\left( \frac{b-a}{2N} \right)}^{5}}=\frac{M{{\left( b-a \right)}^{5}}}{180{{\left( 2N \right)}^{4}}}\]
Para calcular el valor aproximado de la integral se considera el siguiente código.
f=@(x) exp(sin(x));
valor=SimpsonCompuesta(f,0,pi,8)
%6.208757412287802
%Con comando integral Matlab: 6.208758035711110
Para aplicar la expresión de la cota del error, se tiene $a=0$, $b=\pi$, $N=8$. El valor de $M$ se calcula acotando la derivada cuarta de la función $f(x)=e^{sin(x)}$
$$\begin{array}{l}f'\left( x \right) = \cos x\,\,{e^{senx}}\\f''\left( x \right) = {e^{senx}}\left( {cos^2(x)-sen(x) } \right)\\f'''\left( x \right) = -sen(2x){\frac{(sen(x)+3)}{2}} {e^{sen(x)} }\\{f^{iv}}\left( x \right) = \,
{e^{sen(x)}}\left( {5sen^2{{(x)}} - 5sin(x) + 6sen^3{{(x)}} + sen^4{{(x)}} - 3} \right) \end{array}$$
La derivada cuarta es menor que $11$, por lo que una cota del error es $$\left| E \right| \le \frac{{M{\pi ^3}}}{{180{{\left( {2 \cdot 8} \right)}^4}}} \le \frac{{11{\pi ^3}}}{{180{{\left( {2 \cdot 8} \right)}^4}}} \approx {\rm{2}}{\rm{.14345e - 05}}$$
El valor aproximado de la integral se puede calcular con el siguiente código
f=@(x) (1+sin(x.^2));
valor=SimpsonCompuesta(f,0,1,4)
%1.310248532388182
%Con comando integral Matlab: 1.310268301723381
En este caso, se tiene $a=0$, $b=1$, $N=4$. La derivada cuarta de la función $f(x)=1+sen(x^2)$ es
$$\begin{array}{l}f'\left( x \right) = 2x\cos \left( {{x^2}} \right)\\f''\left( x \right) = 2\cos \left( {{x^2}} \right) - 4{x^2}sen\left( {{x^2}} \right)\\f'''\left( x \right) = - 12x\,sen\left( {{x^2}} \right) - 8{x^3}\cos \left( {{x^2}} \right)\\{f^{iv}}\left( x \right) = sen\left( {{x^2}} \right)\left( {16{x^4} - 12} \right) - 48{x^2}\cos \left( {{x^2}} \right)\end{array}$$Teniendo en cuenta que $sen(x)$ y $cos(x)$ son menores que 1 y que $|16x^4-12|$ y $|48x^2|$ son menores que 4 y 48 respectivamente en el intervalo $[0,1]$, la derivada cuarta puede acotarse por
\[M = \mathop {\max }\limits_{x \in \left[ {0,1} \right]} \left| {{f^{iv}}\left( x \right)} \right| \leqslant 52\]Se puede obtener un valor más ajustado calculando el valor máximo de la derivada cuarta en este intervalo que es aproximadamente $28.4283$. Una cota del error sería entonces:
$$\left| E \right| \le \frac{{52}}{{180{{\left( {2 \cdot 4} \right)}^4}}} \approx {\rm{7}}{\rm{.052951388888888e - 05}}$$A continuación, se incluyen algunos ejemplos en los que a partir de ciertos datos tabulados, se realizan distintas aproximaciones del valor de una integral utilizando fórmulas simples o compuestas de cuadratura.
| x | 0 | 15 | 30 | 45 | 60 | 75 | 90 |
|---|---|---|---|---|---|---|---|
| Medida en vertical | 0 | 13 | 14 | 16 | 18 | 15 | 0 |
%Se utiliza la fórmula del trapecio compuesta
x=[0 15 30 45 60 75 90];
d=[0 13 14 16 18 15 0];
%Subintervalos N=6
h=15;%Longitud de cada subintervalo: 90/6
valor=(d(1)+2*sum(d(2:6))+d(7))*h/2
%Otra forma de obtener este valor
%aplicando trapecio a cada intervalo
I=0;
for k=1:6
I=I+(d(k)+d(k+1));
end
I*h/2
Para obtener el valor pedido, se debe tener en cuanta que la región es simétrica y que el valor pedido se solicita en $m^2$.
%Simetría de la región de integración
areaA=2*valor;
%Como el resultado debe estar en m^2
areaTotalA=areaA*10^-4 %0.228000000000000
El valor del área es aproximadamente $0.228 m^2$. Utilizando la fórmula 3/8, el área es $0.2385 \,m^2$.
x=[0 15 30 45 60 75 90];d=[0 13 14 16 18 15 0];
%Subintervalos 2 (en cada uno cuatro puntos)
lonI=45; I1=d(1)+3*d(2)+3*d(3)+d(4);
I2=d(4)+3*d(5)+3*d(6)+d(7);
I=(I1+I2)*lonI/8
%Simetría
areaB=2*I;
%Pasado a m^2
areaTotalB=areaB*10^-4 %0.2385
Utilizando la fórmula de Simpson, el código para calcular el área es el siguiente.
x=[0 15 30 45 60 75 90]; d=[0 13 14 16 18 15 0];
h=30;%Subintervalos 3 (en cada uno tres puntos)
I1=(d(1)+4*d(2)+d(3))*h/6;
I2=(d(3)+4*d(4)+d(5))*h/6;
I3=(d(5)+4*d(6)+d(7))*h/6;
valor=I1+I2+I3;
areaC=2*valor;%Simetría
areaTotalC=areaC*10^-4 %0.24
Se analiza el error absoluto y relativo considerando el valor exacto dado.
areaExacta=0.241356;
format long
errorAbs=abs([areaTotalA areaTotalB areaTotalC]-areaExacta)
errorRel=abs([areaTotalA areaTotalB areaTotalC]-areaExacta)/areaExacta
% errorRelativo1=abs((areaExacta-areaTotalA)/areaExacta)
% errorRelativo2=abs((areaExacta-areaTotalB)/areaExacta)
% errorRelativo3=abs((areaExacta-areaTotalC)/areaExacta)
Los errores calculados, dan como mejor resultado la regla de Simpson.
%Error absoluto
0.013356 0.002856 0.001356
%Error relativo
0.055337344006364 0.011833142743499 0.005618256848804
La concentración promedio de una sustancia que varía con la profundidad se puede calcular de la forma siguiente,
$${c_m} = \frac{{\int\limits_0^H {C\left( z \right)A\left( z \right)dz} }}{{\text{volumen total}}} = \frac{{\int\limits_0^H {C\left( z \right)A\left( z \right)dz} }}{{\int\limits_0^H {A\left( z \right)dz} }}$$Se pide determinar la concentración promedio para $H=16$ considerando los siguientes datos:
| z (m) | 0 | 4 | 8 | 12 | 18 |
|---|---|---|---|---|---|
| $C(z)$ ($g/m^3$) | 10.2 | 8.5 | 7.4 | 5.2 | 4.1 |
| $A(z)$ | 9,82 | 5.11 | 1,96 | 0.393 | 0 |
Utiliza al menos tres reglas de cuadratura.
%Cálculo utilizando la fórmula de los
%trapecios compuesta
z=[0 4 8 12 16];
c=[10.2 8.5 7.4 5.2 4.1];
A=[9.82 5.11 1.96 0.393 0];
%Utilizando la fórmula de los trapecios compuesta (3 subintervalos)
h=4;
masa1=(c(1)*A(1)+2*c(2)*A(2)+2*c(3)*A(3)+2*c(4)*A(4)+c(5)*A(5))*h/2;
vol1=(A(1)+2*A(2)+2*A(3)+2*A(4)+A(5))*h/2;
concentracion=masa1/vol1
%Cálculo utilizando Simpson compuesta (2 subintervalos)
h=8;
I1=c(1)*A(1)+4*c(2)*A(2)+c(3)*A(3);
I2=c(3)*A(3)+4*c(4)*A(4)+c(4)*A(5);
masa2=(I1+I2)*h/6;
I3=A(1)+4*A(2)+A(3);
I4=A(3)+4*A(4)+A(5);
vol2=(I3+I4)*h/6;
concentracion2=masa2/vol2
%Fórmula utilizando n=4 (5 nodos) Regla de Millne
h=16;
pesos=[7 32 12 32 7];
masa3=sum(pesos.*c.*A)*h/90;
vol3=sum(pesos.*A)*h/90;
concentracion3=masa3/vol3
Debido a restricciones experimentales, solo se ha registrado la siguiente información:
| x (m) | 0 | 2.5 | 5 | 10 | 12.5 | 15 | 20 | 25 | 30 |
|---|---|---|---|---|---|---|---|---|---|
| $F(x)$ (Newton) | 0 | 6 | 9 | 13 | 13.5 | 14 | 10.5 | 12 | 5 |
| $\theta(x)$ (radianes) | 0.5 | 0.76 | 1.4 | 0.75 | 0.57 | 0.9 | 1.3 | 1.48 | 1.5 |
Calcula el trabajo (W) realizado por el bloque en su recorrido considerando toda la información recogida en la tabla.
%Datos
x=[0 2.5 5 10 12.5 15 20 25 30];
F=[0 6 9 13 13.5 14 10.5 12 5];
theta=[0.5 0.76 1.4 0.75 0.57 0.9 1.3 1.48 1.5];
%Función a integrar
fxint=F.*cos(theta);
%En [0, 5] Regla de Simpson
lon1=5;
I1=(fxint(1)+4*fxint(2)+fxint(3))*lon1/6
%En [5,10] Regla del Trapecio
lon2=5;
I2=(fxint(3)+fxint(4))*lon2/2
%En [10, 15] Regla de Simpson 1/3
lon3=5;
I3=(fxint(4)+4*fxint(5)+fxint(6))*lon3/6
%En [15, 30] Regla 3/8
lon4=15;
I4=(fxint(6)+3*fxint(7)+3*fxint(8)+fxint(9))*lon4/8
%El Trabajo en [0, 30]
W=I1+I2+I3+I4
%Solución W=135.3398
En Los métodos compuestos se considera que la longitud de cada subintervalo es siempre igual, por lo que no se tiene en cuenta el comportamiento de la función. En este apartado se mostrarán métodos en los que se realizan subdivisiones del intervalo con mayor error estimado hasta alcanzar una tolerancia establecida. Así, dependiendo de la función, puede ser conveniente utilizar subintervalos más pequeños donde haya más variabilidad de la función.
En primer lugar, se calcula la aproximación $\color{blue}{I_1}$ de la integral de $f$ en $[a,b]$ mediante la cuadratura de los trapecios.
Además, se considera $\color{red}{I_2}$ la aproximación de la integral utilizando la regla del trapecio compuesta con $N=2$ siendo $ \color{red}{E}$ el error de esta aproximación.
Se tendrá:
$$\int\limits_a^b {f\left( x \right)dx} = I_1 - {\color{blue}{\frac{(b-a)^3}{12} f''(\xi _1)}}$$ $$\int\limits_a^b {f\left( x \right)dx} = I_2 {\color{red}{-\frac{(b-a)^3}{12 \cdot 4} f''(\xi _2)}}=I_2+ {\color{red}{E}}$$Si se considera $\color{red}{I_2}$ como valor de la integral, y se supone que $f''(\xi _1)\approx f''(\xi _2)$, restando las dos expresiones anteriores, una estimación del error sería
$$\left|I_2-I_1\right| \approx \left | \color{red}{E}-\color{blue}{4E} \right|= \left |3E\right|$$ $$\color{red}{\left |E\right|\approx \left |\frac{1}{3}(I_2-I_1)\right|}$$Teniendo en cuenta esta estimación del error, se puede establecer un método recursivo para calcular la integral de $f$ en $[a, b]$ con un error inferior a un valor dado. El método consiste en aplicar los siguientes pasos.
Calcula el volumen para $H=16$ utilizando la fórmula de cuadratura de los trapecios y la fórmula de cuadratura compuesta de los trapecios con $N=2$ a partir de los siguientes datos dando una estimación del error de cada aproximaicón.
| z (m) | 0 | 4 | 8 | 12 | 16 |
|---|---|---|---|---|---|
| $A(z)$ | 9.82 | 5.11 | 1.96 | 0.393 | 0 |
A=[9.82 5.11 1.96 0.393 0];
disp('Cálculos aproximados de la integral')
I2=(A(1)+2*A(3)+A(5))*8/2 %54.960000000000001
I1=(A(1)+A(5))*16/2 %78.560000000000002
Se calculan las estimaciones del error en cada caso.
%Considerando I2 como valor de la integral
estimE2=abs(I2-I1)/3
%7.866666666666667
%Considerando I1 como valor de la integral
estimE1=abs(I2-I1)*4/3
%31.466666666666669
f = @(x) log(1 + x) ./ (1 + x.^2);
a = 0; b = 1; tol = 1e-3;
Se define una función Matlab para calcular la fórmula de cuadratura de los trapecios para $N=2$ de $f$ en $[a,b]$, dando también la estimación del error que se obtendría al considerar este valor como aproximación. Además, según la estimación del error, se muestra un mensaje indicando si éste está por debajo de la tolerancia establecida o si, en caso contrario, es necesario subdividir el intervalo para lograrlo.
function [S,estE]=PasoTrapAdaptativo(f,a,b,tol)
I1=Trapecio(f,a,b);
xm=(a+b)/2;
I2=Trapecio(f,a,xm)+Trapecio(f,xm,b);
S=I2;
estE=abs(I1-I2)/3;
if estE>tolerancia
disp('Dividir el intervalo')
else
disp('Estimación inferior a la permitida')
end
end
Para aplicar el método adaptativo, se considera el intervalo $\color{magenta}[0,1]$ y se analiza, con ayuda de la función anterior, si la estimación de la aproximación es inferior a la tolerancia, tol.
[S,est]=PasoTrapAdaptativo(f,0,1,tol);
%Se debe dividir el intervalo [0,1]
Como no se cumple que el error sea menor que la tolerancia, se divide el intervalo $[0,1]$ y se repite el proceso en $[0, 0.5]$ y $[0.5,1]$ buscando que el error estimado sea inferior a tol/2 en cada intervalo.
Se repite el proceso para calcular la integral en $\color{red}{[0, 0.5]}$ con error inferior a tol/2.
%[0, 0.5] tol/2
[S,est]=PasoTrapAdaptativo(f,0,0.5,tol/2);
%Se debe dividir el intervalo [0, 0.5]
De nuevo, hay que dividir el intervalo $[0, 0.5]$ y repetir el proceso con los intervalos $[0,0.25]$ y $[0.25,0.5]$ buscando ahora que la estimación sea inferior a tol/4.
Se analiza $\color{green}[0, 0.25]$.
%[0, 0.25] tol/4
[S,est]=PasoTrapAdaptativo(f,0,0.25,tol/4);
%Se debe dividir el intervalo [0, 0.25]
Se debe dividir el intervalo $[0, 0.25]$ y repetir el proceso con los intervalos $[0, 0.125]$ y $[0.125,0.25]$ considerando tol/8.
%[0, 0.125] tol/8
[S,est]=PasoTrapAdaptativo(f,0,0.125,tol/8);
%Se cumple
Dado que sí se cumple con la tolerancia establecida, se considera el valor S como la aproximación de la integral en $[0, 0.125]$ .
val1=S %0.007398388926458
Se analiza $[0.125, 0.25]$ y se comprueba que también se cumple con la tolerancia permitida, así que se considera el valor de la integral en ese intervalo como S.
%[0.125, 0.25] tol/8
[S,est]=PasoTrapAdaptativo(f,0.125,0.25,tol/8);
%Se cumple
val2=S %0.020563003600857
Hasta este momento se tiene calculado el valor de la integral en $[0, 0.25]$ con la tolerancia adecuada. Se analiza $\color{green}{ [0.25,0.5]}$ con tol/4.
%[0.25, 0.5] tol/4
[S,est]=PasoTrapAdaptativo(f,0.25,0.5,tol/4);
%Se debe dividir el intervalo [0.25 0.5]
Como el error no es inferior, se divide el intervalo $[0.25, 0.5]$ buscando que el valor de la integral en $[0.25, 0.375]$ y $[0.375, 0.5]$ tenga un error inferior a tol/8.
%[0.25, 0.375] tol/8
[S,est]=PasoTrapAdaptativo(f,0.25,0.375,tol/8);
%Se cumple
val3=S %0.030771575660209
%[0.375, 0.5] tol/8
[S,est]=PasoTrapAdaptativo(f,0.375,0.5,tol/8);
%Se cumple
val4=S %0.037899052702097
Se ha calculado el valor de la integral en $[0.25, 0.5]$ con la tolerancia adecuada. Se analiza $\color{red}{ [0.5,1]}$ con una estimación del error inferior a tol/2.
%[0.5, 1] tol/2
[S,est]=PasoTrapAdaptativo(f,0.5,1,tol/2);
%Se debe dividir el intervalo [0.5 1]
Como el error no es inferior, se considera el valor de la integral en $[0.5, 0.75]$ y $[0.75, 1]$ con error inferior a tol/4.
Se analiza $\color{green}[0.5, 0.75]$.
%[0.5, 0.75] tol/4
[S,est]=PasoTrapAdaptativo(f,0.5,0.75,tol/4);
%Se debe dividir el intervalo [0.5 0.75]
Como el error no es inferior, se considera el valor de la integral en $[0.5, 0.625]$ y $[0.625, 1]$ con tol/8.
%[0.5, 0.625] tol/8
[S,est]=PasoTrapAdaptativo(f,0.5,0.625,tol/8);
%Se cumple
val5=S %0.042235620867100
%[0.625, 0.75] tol/8
[S,est]=PasoTrapAdaptativo(f,0.625,0.75,tol/8);
%Se cumple
val6=S %0.044309421526304
Se ha calculado el valor de la integral en $[0.5, 0.75]$ con la tolerancia adecuada. Se analiza $\color{green}{ [0.75,1]}$ con tol/4.
Se analiza $\color{green}[0.75, 1]$.
%[0.75, 1] tol/4
[S,est]=PasoTrapAdaptativo(f,0.75,1,tol/4);
%Se cumple
val7=S %0.088548748833623
Por lo tanto, el valor de la integral será la suma de los valores obtenidos en
disp('El valor de la integral es')
val1+val2+val3+val4+val5+val6+val7 %0.271725812116648
%Cálculo dado con Matlab/Octave
integral(f,0,1) % 0.272198261287950
En la siguiente imagen se representa las distintas divisiones realizadas en el ejemplo.
Se da a continuación el código del programa del método recursivo de la fórmula de cuadratura adaptativa que tendrá como argumentos, la función a integrar, el extremo inferior y superior del intervalo de integración, y la tolerancia permitida en la aproximación.
function valor=TrapecioAdaptativa(f,a,b,tol)
%Aproxima la integral de f en el intervalo [a,b]
%usando la regla del trapecio adaptativa
%en forma recursiva
%Trapecios en [a,b]
I1=(f(a)+f(b))*(b-a)/2;
%Punto medio del intervalo
xm=(a+b)/2;
%Trapecios en [a,xm] y en [xm,b]
I2=(f(a)+f(xm))*(xm-a)/2+(f(xm)+f(b))*(xm-a)/2;
%También: (f(a)+2*f(xm)+f(b))*(xm-a)/2;
%Estimación del error considerando I2
$como valor aproximado de la integral
error=abs(I1-I2)/3;
if error<tol
valor=I2;
else
%Si la estimación no es la deseada
%se aplica el proceso en [a, xm] y [xm, b]
%con error inferior en cada uno a tol/2
valor= TrapecioAdaptativa(f,a,xm,tol/2)+
TrapecioAdaptativa(f,xm,b,tol/2);
end
end
Para calcular el valor de la integral, se deberá escribir el siguiente código.
f=@(x) 1+sin(x.^2);
TrapecioAdaptativa(f,0,1,10^-5)
%Devuelve el valor 1.310271922110889
%Con comando integral de Matlab: 1.310268301723381
De forma análoga, llamando $I_1$ al cálculo de la integral de $f(x)$ en $[a,b]$ con la fórmula de cuadratura de Simpson e $I_2$ al cálculo con la fórmula de cuadratura de Simpson compuesta con $N=2$, se tendrá,
$$\int\limits_a^b {f\left( x \right)dx} = I_1 -{\color{blue}{ \frac{h^5}{90 } f^{iv}(\xi _1)}}$$ $$\int\limits_a^b {f\left( x \right)dx} = I_2 - {\color{red}{\frac{h^5}{90 \cdot 2^4 } f^{iv}(\xi _2)}}=I_2+\color{red}{E}$$siendo $h=(b-a)/2$.
Si se supone que $f^{(iv}(\xi _1)\approx f^{(iv}(\xi _2)$, restando las dos expresiones anteriores, se puede considerar que una estimación del error considerando como valor de la integral $I_2$ será
$$\left|I_2-I_1\right| \approx \left |E-16E \right|= \left |15E\right|$$ $$\color{red}{\left |E\right|\approx \left |\frac{1}{15}(I_2-I_1)\right|}$$Teniendo en cuenta la estimación anterior del error, el método recursivo para obtener una aproximación de la integral con una cierta tolerancia, consiste en aplicar los siguientes pasos.
A partir de los datos siguientes, se pide calcular la aproximación del volumen para $H=16$ empleando la cuadratura compuesta de Simpson con $N=2$.
| z (m) | 0 | 4 | 8 | 12 | 16 |
|---|---|---|---|---|---|
| $A(z)$ | 9.82 | 5.11 | 1.96 | 0.393 | 0 |
Dar una estimación del error que se comete al considerar como volumen para $H=16$ esta aproximación.
A=[9.82 5.11 1.96 0.393 0];
I2=(A(1)+4*A(2)+4*A(4)+2*A(3)+A(5))*8/6 %47.6693
%También:
%(A(1)+4*A(2)+A(3))*8/6+(A(3)+4*A(4)+A(5))*8/6
Una estimación del error será:
I1=(A(1)+4*A(3)+A(5))*16/6 %47.0933
%Considerando I2 como valor de la integral
estimE2=abs(I2-I1)/15 %0.0384
%De considerar I1 como valor de la integral
estimE1=abs(I2-I1)*16/15 %0.6144
f = @(x) log(1 + x) ./ (1 + x.^2);
a = 0; b = 1;
tol = 1e-5;
Se define una función Matlab para calcular la fórmula de cuadratura de Simpson para $N=2$ de $f$ en $[a,b]$, dando también la estimación del error que se obtendría al considerar ese valor como aproximación. Asimismo, tras comparar la estimación del error con la tolerancia establecida, se imprime un mensaje en pantalla que informa si el error está dentro del margen permitido o, de lo contrario, se debe dividir el intervalo para cumplir con dicha tolerancia.
function [S,estE]=PasoSimponAdaptativo(f,a,b,tol)
I1=Simpson(f,a,b);
xm=(a+b)/2;
I2=Simpson(f,a,xm)+Simpson(f,xm,b);
S=I2;
estE=abs(I1-I2)/15;
if estE>tolerancia
disp('Dividir el intervalo')
else
disp('Estimación inferior a la permitida')
end
end
Se considera en primer lugar el intervalo $\color{magenta}[0,1]$ y se estima el error para ver si es inferior a la tolerancia establecida, tol.
[S,est]=PasoSimponAdaptativo(f,0,1,tol)
%No se cumple que sea menor que tol
Como no se cumple, se divide el intervalo $[0,1]$ y se repite el proceso en $[0, 0.5]$ y $[0.5,1]$ buscando que el error estimado sea inferior a tol/2.
Se calcula la integral en $\color{red}{[0, 0.5]}$ con error inferior a tol/2.
[S,est]=PasoSimponAdaptativo(f,0,0.5,tol/2)
%No se cumple que es inferior a tol/2
Se divide el intervalo $[0,0.5]$ en dos subintervalos, $[0, 0.25]$ y $[0.25, 0.5]$, repitiendo el proceso considerando el error inferior a tol/4.
Se analiza $\color{green}{[0, 0.25]}$.
%Se ve si en [0,0.25] el error es menor que tol/4
[S,est]=PasoSimponAdaptativo(f,0,0.25,tol/4)
%Se cumple que es inferior a tol/4
En este caso, se toma S como el valor de la integral en $[0, 0.25]$
valor1=S
%Se obtiene en [0, 0.25]: 0.028074368412078
Se analiza $\color{green}{ [0.25, 0.5]}$.
%Se ve si en [0,25,0.5] el error es menor que tol/4
[S,est]=PasoSimponAdaptativo(f,0.25,0.5,tol/4)
%Se cumple que es inferior a tol/4
Como el error es inferior, se considera S como el valor de la integral en $[0.25, 0.5]$
valor2=S
%Resultado en [0.25, 0.5]: 0.068795007885837
Se analiza $\color{red}{ [0.5,1]}$
[S,est]=PasoSimponAdaptativo(f,0.5,1,tol/2)
%Se cumple que es inferior a tol/2
Como el error es inferior, se considera el valor de la integral en $[0.5, 1]$ el dado por S.
valor3=S
%Resultado en [0, 0.5]: 0.175328138427274
Por lo tanto, el valor de la integral será la suma de los valores obtenidos en
disp('El valor de la integral es')
valor1+valor2+valor3 %0.272197514725190
%Calculo dado con Matlab/Octave
integral(f,0,1) %0.272198261287950
En la siguiente imagen se representa las distintas divisiones realizadas en el ejemplo.
En primer lugar se considera la función que permite obtener de forma recursiva la aproximación de la integral con una cierta tolerancia aplicando el método recursivo adaptativo de Simpson. Se utiliza la función Simpson que calcula la aproximación de la integral de una función en un intervalo mediante esta fórmula de cuadratura.
function valor=SimpsonAdaptativa(f,a,b,tol)
%Simpson en [a,b]
I1=Simpson(f,a,b);
%Simpson en [a,puntoMedio] y [puntoMedio,b]
%Punto medio
xm=(a+b)/2;
I2=Simpson(f,a,xm)+Simpson(f,xm,b);
%Estimación del error al considerar
%I2 como aproximación de la integral
E=abs(I2-I1)/15;
if E<tol
valor=I2;
else
%Si la estimación del error es superior
%a la tolerancia se aplica el mismo
%proceso en [a,xm] y [xm,b] con tol/2
J1=SimpsonAdaptativa(f,a,xm,tol/2);
J2=SimpsonAdaptativa(f,xm,b,tol/2);
valor=J1+J2;
end
end
Para aproximar la integral pedida, bastará escribir el siguiente código.
f=@(x) 1+sin(x.^2);
SimpsonAdaptativa(f,0,1,10^-5)
%Devuelve: 1.310264088438636
Se define la función a integrar y se ejecuta SimpsonAdaptativa considerando $a=0$, $b=1$ y $tol=10^-12$.
f=@(x) exp(sin(x).*cos(x));
SimpsonAdaptativa(f,0,pi,10^-12)
%Devuelve el valor 3.341031544735790
Se define la función a integrar y se ejecuta SimpsonAdaptativa considerando $a=0$, $b=4$ y $tol=10^-12$.
f=@(x) exp(-x.^2);
SimpsonAdaptativa(f,0,4,10^-12)
%Devuelve el siguiente valor 0.886226911789732
En este apartado se verá cómo encontrar una estimación del error cuando se utiliza una fórmula de Newton-Cotes considerando dos pasos diferentes $h$ y $h/2$ y una estrategia para aplicar este método adaptativo en general.
Si se llama $I$ a la aproximación de la integral
$$\int\limits_a^b {f\left( x \right)dx} = I + E \,\,\, \text{con} \,\,E = {C_n}{h^{m + 1}}{f^{(m}}\left( \xi \right)$$ siendo $$m = \left\{ \begin{aligned} & n + 1\,\,si\,\,n\,\,impar \\ & n + 2\,\,si\,\,n\,\,par \\ \end{aligned} \right.$$Aplicando la misma fórmula a los intervalos $[a,\frac{a+b}{2}]$ y $[\frac{a+b}{2},b]$ se tendrá,
$$\begin{aligned} \int\limits_a^{\frac {a+b}{2}} {f\left( x \right)dx} &= {I_1} + {E_1} = {I_1} + {C_n}{\left( {{h \over 2}} \right)^{m + 1}}{f^{(m}}\left( {{\xi _1}} \right)\\ & {\xi _1} \in \left[ {a,{{a + b} \over 2}} \right] \end{aligned}$$ $$\begin{aligned} \int\limits_{{{a + b} \over 2}}^b {f\left( x \right)dx} &= {I_2} + {E_2} = {I_2} + {C_n}{\left( {{h \over 2}} \right)^{m + 1}}{f^{(m}}\left( {{\xi _2}} \right)\\ &{\xi _2} \in \left[ {{{a + b} \over 2},b} \right] \end{aligned}$$Entonces, $$I + E{\mkern 1mu} {\mkern 1mu} = {I_1} + {I_2} + {C_n}{{{h^{m + 1}}} \over {{2^m}}}\left[ {{{{f^{(m}}\left( {{\xi _1}} \right) + {f^{(m}}\left( {{\xi _2}} \right)} \over 2}} \right]$$ Si $[a,b]$ es pequeño, $$I + E{\mkern 1mu} {\mkern 1mu} \approx {I_1} + {I_2} + \underbrace {{C_n}{{{h^{m + 1}}} \over {{2^m}}}{f^{(m}}\left( \xi \right)}_{E/{2^m}}$$ $$I + E \approx {I_1} + {I_2} + {E \over {{2^m}}}$$ $${{{2^m} - 1} \over {{2^m}}}E \approx {I_1} + {I_2} - I$$ $$E \approx {{{2^m}} \over {{2^{m}-1}}}\left( {{I_1} + {I_2} - I} \right)$$
Por lo tanto, fijada una precisión $\epsilon$ deseada de la integral, se describe la estrategia para obtener la aproximación con la precisión deseada.
[itg error]=iehardy(a,b,f)
%Devuelve tanto la estimación de la integral como
%el error cometido. Requiere que la
%función f se programe vectorialmente.
Se definen los datos del problema.
a=0;b=pi;
format long
f=@(x) exp(sin(x).*cos(x));
error=10^-12;
Se divide el intervalo en dos partes y se aplica la fórmula de Newton-Cotes de Hardy. Se tendrá que
x=[a (a+b)/2 b];
[i1 e1]=iehardy(x(1),x(2),f);
[i2 e2]=iehardy(x(2),x(3),f);
E=[e1 e2];I=[i1 i2];
error=sum(E)
itg=sum(I)
Si el error es menor que $\epsilon_a$ se habrá terminado y el valor de la integral es itg. Como en este caso no es así, se considera el subintervalo con mayor error. Ejecutando la orden,
[s k]=max(E)
El valor que se obtiene es $k=1$, Se continúa repitiendo el proceso en el intervalo $[x(k),x(k+1)]$ hasta conseguir la precisión considerada.
Los vectores $x$, $E$, $I$ van creciendo según se van tomando subdivisiones en los intervalos.
xn=(x(k)+x(k+1))/2;
x=[x(1:k) xn x(k+1:end)];
[i1 e1]=iehardy(x(k),xn,f);
[i2 e2]=iehardy(xn,x(k+2),f);
E=[E(1:k-1) e1 e2 E(k+1:end)]
I=[I(1:k-1) i1 i2 I(k+1:end)];
itg=sum(I)
error=sum(E)
Se repite el proceso 26 veces obteniendo que el valor de la integral es $ 3.341031544735853$.
Nota: El
valor que devuelve matlab con el comando integral(f,0,pi) es $3.341031544735852$.
Usualmente, si la integral es un número grande, el algoritmo se detiene cuando el error relativo es inferior a $\epsilon_r$, mientras que si $|I|$ es pequeño, el algoritmo finaliza cuando el error absoluto es inferior a $\epsilon_a$.
Se muestra a continuación, el código general a ejecutar con Matlab/Octave.
%ea error absoluto
%er error relativo
%Se definen los extremos del intervalo
%y el punto medio
x=[a (a+b)/2 b]
%Se aplica la cuadratura de Hardy en [a, xm]
[i1 e1]=iehardy(x(1),x(2),f)
%Se aplica la cuadratura de Hardy en [xm, b]
[i2 e2]=iehardy(x(2),x(3),f)
%Se almacenan los valores de las integrales y
%la estimación de los errores
I=[i1 i2];E=[e1 e2];
error=sum(E);
%Se comprueba si el error es menor que
%el error absoluto considerado
if error<ea
itg=sum(I);
[itg error]
else
%Se considera el subintervalo con mayor error
[s,k]=max(E)
end
parar=0
%Se repite el proceso hasta conseguir la
%precisión dada
while parar==0
xn=(x(k)+x(k+1))/2
x=[x(1:k) xn x(k+1:end)]
[i1 e1]=iehardy(x(k),xn,f);
[i2 e2]=iehardy(xn,x(k+2),f);
E=[E(1:k-1) e1 e2 E(k+1:end)];
I=[I(1:k-1) i1 i2 I(k+1:end)];
error=sum(E);
if error < ea+er*abs(itg)
itg=sum(I);
[itg error]
parar=1;
else
[s,k]=max(E);
end
end
En este apartado, se verá cómo proceder cuando el intervalo $[a,b]$ no es acotado o cuando la función $f$ tiene una singularidad en un punto $x_0$ en $[a,b]$ de forma que $\mathop {\lim }\limits_{x \to {x_o}} \left| {f\left( x \right)} \right| = +
\infty $. En el primer caso, se denominan
Para estas integrales se considera que los límites de integración $a$ o $b$ o ambos, no son finitos.
con $f$ una función continua para la cual la integral es convergerte, esto es, el límite anterior existe. En consecuencia, se tendrá que
$$\mathop {\lim }\limits_{b \to \infty } \int\limits_b^\infty {f\left( x \right)dx} = 0$$Teniendo esto en cuenta, el valor aproximado de la integral con un error inferior a un valor fijado, $\epsilon$, se obtendrá siguiendo los siguientes pasos.
se tendrá en cuenta que $$\int\limits_{ - \infty }^\infty {f\left( x \right)dx} = \int\limits_{ - \infty }^0 {f\left( x \right)dx} + \int\limits_0^\infty {f\left( x \right)dx} $$
Se procederá entonces buscando una aproximación de cada una de ellas con un error menor que $\epsilon/2$. Alternativamente se pueden buscar números $a<0$ y $b>0$ de forma que
$$\left| {\int\limits_{ - \infty }^a {f\left( x \right)dx} } \right| < {\varepsilon \over 4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| {\int\limits_b^\infty {f\left( x \right)dx} } \right| < {\varepsilon \over 4}\,\,\,\,\,\,\,\,\,\left| {\int\limits_a^b {f\left( x \right)dx} } \right| < {\varepsilon \over 2}$$Esta integral es impropia de primera especie, del tipo I. Dado que
$$\int\limits_0^\infty {{e^{ - x}}{{\cos }^2}\left( x \right)dx} = \underbrace {\int\limits_0^b {{e^{ - x}}{{\cos }^2}\left( x \right)dx} }_{ = {I_1}} + \underbrace {\int\limits_b^\infty {{e^{ - x}}{{\cos }^2}\left( x \right)dx} }_{ = {I_2}}$$ se calculará el valor de la integral, siguiendo los siguientes pasos:Teniendo en cuenta que
\[\left| {\int\limits_b^\infty {{e^{ - x}}{{\cos }^2}xdx} } \right| \leqslant \int\limits_b^\infty {\left| {{e^{ - x}}{{\cos }^2}x} \right|dx} \leqslant \int\limits_b^\infty {{e^{ - x}}dx} = \frac{1}{{{e^b}}}\]basta obtener $b$ cumpliendo
\[\frac{1}{{{e^b}}} < \frac{{{{10}^{ - 12}}}}{2}\] Puede considerarse cualquier $b$ cumpliendo ${\log \left( {2 \cdot {{10}^{12}}} \right) \le b}$, por ejemplo, $b=28.4$.El valor de la integral siguiendo este proceso es $0.599999999999007$.
f=@(x) exp(-x).*cos(x).^2;
SimpsonAdaptativa(f,0,28.5,10^-12/2)
%Valor 0.599999999999479
En este caso, se considera $f\left( x \right) = {e^{ - x}}\log \left( {2 + {\text{sen}}x} \right)$. Se escribe la integral pedida de la forma siguiente,
\[\int\limits_0^\infty {f\left( x \right)dx} = \underbrace {\int\limits_0^b {f\left( x \right)dx} }_{{I_1}} + \underbrace {\int\limits_b^\infty {f\left( x \right)dx} }_{{I_2}}\]Se busca $b$ cumpliendo
\[\left| {\int\limits_b^\infty {{e^{ - x}}\log \left( {2 + {\text{sen}}x} \right)dx} } \right| \leqslant \int\limits_b^\infty {{e^{ - x}}\log 3\,dx} = \frac{{\log 3}}{{{e^b}}} \leqslant \frac{{{{10}^{ - 12}}}}{2}\]Despejando el valor de $b$ se debe cumplir,
\[b \geqslant \log \left( {2\log 3 \cdot {{10}^{12}}} \right) \approx {\text{11.978886494563813}}\]Se toma $b=11.98$ y se calcula $I_1$ con un error menor que $\frac{10^{ - 12}}{2}$.
f=@(x) exp(-x).*log(2+sin(x));
SimpsonAdaptativa(f,0,11.98,10^-12/2)
%Valor 0.902221166208351
La solución que da Matlab con el comando integral es 0.902221166208359
En este tipo de integrales la función $f$ es continua en $[a,b]$ salvo en un punto $x_0$ del intervalo donde $$\mathop {\lim }\limits_{x \to {x_0}} \left| {f\left( x \right)} \right| = + \infty $$
Se procede de la siguiente forma:
En este caso la singularidad está en el punto $0$ por lo que se deberá buscar un valor $\delta$ de forma que si se considera
\[\int\limits_0^1 {f\left( x \right)dx} = \underbrace {\int\limits_0^\delta {f\left( x \right)dx} }_{{I_1}} + \underbrace {\int\limits_\delta^1 {f\left( x \right)dx} }_{{I_2}}\] las dos integrales $I_1$ e $I_2$ cumplan que en valor absoluto son menores que $\epsilon/2$.Como $sen(x)$ es mayor que $2x/\pi$ en $[0,\pi/2]$ en el entorno de $0$ se tiene que se cumple,
\[\left| {\int\limits_0^\delta {\frac{{\cos x}}{{2\pi \,\,\,sen\left( {\sqrt x } \right)}}} } \right| \leqslant \int\limits_0^\delta {\frac{{dx}}{{\pi \,\,\pi \sqrt x }}} = \frac{{\sqrt \delta }}{{{2\pi ^2}\,}} \leqslant \frac{{{{10}^{ - 12}}}}{2}\]El valor de $\delta$ puede ser cualquier valor menor que $2.435227275850061e-23$. Con este valor se calcula $I_2$ para que sea menor que $\epsilon/2$.
Solución Matlab: 0.302993744656398En este capítulo, se aborda la integración numérica, una herramienta fundamental para calcular integrales cuando las soluciones analíticas no son posibles o resultan dificiles de obtener. Se describen métodos numéricos y se evalúa su precisión. Además, se estudian métodos específicos para tratar integrales impropias y se analizan los errores asociados a estas aproximaciones.
Los principales aspectos tratados en este tema son los siguientes.
Se muestran las fórmulas de cuadratura que aproximan la integral de una función en un intervalo mediante la interpolación polinómica en un número de nodos.
En particular, se analizan las fórmulas de Newton-Cotes donde los puntos se consideran equidistantes y se incluyen los extremos del intervalo. Se incluyen ejemplos donde se muestra su utilidad y se analizan los errores asociados.
Se extienden las fórmulas de Newton-Cotes a subintervalos más pequeños, mejorando la precisión para integrales de funciones complejas. Además, se introducen métodos adaptativos que ajustan dinámicamente los intervalos según la función.
Se presentan métodos para evaluar integrales impropias diferenciando entre las de primera y segunda especie. En el primer caso el intervalo de integración no es acotado y en el segundo la función presenta una singularidad dentro del intervalo de integración.
El capítulo incluye ejemplos prácticos y ejercicios para aplicar y comprender los conceptos, así como autoevaluaciones para reforzar el aprendizaje.

En Ingeniería, el comportamiento de un sistema suele describirse mediante ecuaciones que relacionan la tasa de cambio de una magnitud con la propia magnitud y otras variables asociadas. De hecho, muchas leyes físicas se establecen en términos de razones de cambio, como ocurre en fenómenos relacionados con la caída de un cuerpo o la variación de la temperatura, entre otros. Estas relaciones se representan comúnmente mediante ecuaciones diferenciales ordinarias (EDOs), unas ecuaciones que vinculan una función de una única variable independiente con sus derivadas, describiendo formalmente cómo cambia dicha función respecto de esa variable.
Dado que las EDOs suelen ser complejas y a menudo no tienen solución explícita o resulta difícil de obtener, se necesita recurrir a métodos numéricos para aproximarlas.
En este capítulo se estudiará la resolución numérica de dos problemas asociados a las ecuaciones diferenciales ordinarias:
Como ejemplo de ecuación diferencial, se muestra en el interactivo 6.1 un ejemplo de aplicación para el análisis de un sistema masa-resorte. Este sistema está compuesto por una masa \( m \) unida a un resorte que ejerce una fuerza proporcional al desplazamiento, según la ley de Hooke. Si además se considera una fuerza de amortiguamiento proporcional a la velocidad, se obtiene la siguiente ecuación diferencial de segundo orden:
\( m \frac{d^2x}{dt^2} + c \frac{dx}{dt} + kx = 0 \)
donde:
En el siguiente ejemplo, las ecuaciones diferenciales modelizan al vaciado de un tanque. Asumiendo que el flujo de salida obedece la ley de Torricelli, la velocidad de vaciado es proporcional a la raíz cuadrada de la altura del líquido. Esto lleva a una ecuación diferencial de la forma:
\( \frac{dh}{dt} = -k \sqrt{h} \)
donde:
En su forma general, se considera
$$y\left( t \right) = \left( \begin{aligned} &{{y_1}\left( t \right)} \\ & {{y_2}\left( t \right)} \\ &\vdots \\ & {{y_n}\left( t \right)} \\ \end{aligned} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,f\left( {t,y\left( t \right)} \right) = \left( \begin{aligned} & {{f_1}\left( {t,{y_1},{y_2},...,{y_n}} \right)} \\ &{{f_2}\left( {t,{y_1},{y_2},...,{y_n}} \right)} \\ & \vdots \\ &{{f_n}\left( {t,{y_1},{y_2},...,{y_n}} \right)} \\ \end{aligned} \right)$$ $$\begin{aligned} & y'_1={{f_1}\left( {t,{y_1},{y_2},...,{y_n}} \right)} \\ & y'_2={{f_2}\left( {t,{y_1},{y_2},...,{y_n}} \right)} \\ & \vdots \\ & y'_n={{f_n}\left( {t,{y_1},{y_2},...,{y_n}} \right)} \\ \end{aligned}$$Esta forma general permite escribir muchos problemas. Se muestran algunos ejemplos.
Llamando
$${y_1} = y \,\,\,\,\,\,\,\,{y_2} = y'$$ se puede escribir $$\left\{ \begin{aligned} & y{'_1} = {y_2} \\ & y{'_2} = 1 - {y_1} \\ & y_1(0)=1, \,\,\,\,y_2(0)=1 \end{aligned} \right.$$Considerando
$$y\left( t \right) = \left( \begin{aligned} {{y_1}\left( t \right)} \\ {{y_2}\left( t \right)} \\ \end{aligned} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,f\left( {t,y\left( t \right)} \right) = \left( \begin{aligned} {{y_2}} \\ {1- {y_1}} \\ \end{aligned} \right)$$la ecuación diferencial puede escribirse de la forma
$$ \left( \begin{aligned} {{y'_1}\left( t \right)} \\ {{y'_2}\left( t \right)} \\ \end{aligned} \right)=\left( \begin{aligned} {{y_2}} \\ {1- {y_1}} \\ \end{aligned} \right)$$con las siguientes condiciones en el punto inicial $t_0=0$
$$y\left( 0 \right) = \left( \begin{aligned} 1 \\ 1 \\ \end{aligned} \right)$$Llamando
$${y_1} = y \,\,\,\,\,\,\,\,{y_2} = y'$$ se puede escribir $$\left\{ \begin{aligned} & y{'_1} = {y_2} \\ & y{'_2} = 2t{y_1} +t^2\\ & y_1(0)=1, \,\,\,\,y_2(0)=0 \end{aligned} \right.$$Considerando
$$y\left( t \right) = \left( \begin{aligned} &{{y_1}\left( t \right)} \\ & {{y_2}\left( t \right)} \\ \end{aligned} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,f\left( {t,y\left( t \right)} \right) = \left( \begin{aligned} {{y_2}} \\ {2t{y_1} + {t^2}} \\ \end{aligned} \right)$$la ecuación diferencial puede escribirse de la forma
$$ \left( \begin{aligned} {{y'_1}\left( t \right)} \\ {{y'_2}\left( t \right)} \\ \end{aligned} \right)=\left( \begin{aligned} {{y_2}} \\ {2t {y_1}+t^2} \\ \end{aligned} \right)$$con las siguientes condiciones en el punto inicial
$$y\left( 0 \right) = \left( \begin{aligned} 1 \\ 0 \\ \end{aligned} \right)$$Considerando ${x_1} = x\left( t \right)\,\,\,\,\,{x_2} = x'\left( t \right)$, se podrá escribir
$$ \left( \begin{aligned} {{x'_1}\left( t \right)} \\ {{x'_2}\left( t \right)} \\ \end{aligned} \right)=\left( \begin{aligned} {{x_2}} \\ {-4x_1 +20 sen(0.5t)} \\ \end{aligned} \right)$$Las condiciones en el punto inicial son $\left( \begin{aligned} x_1(0) \\ x_2(0) \\ \end{aligned} \right)= \left( \begin{aligned} 0 \\ 0 \\ \end{aligned} \right)$
Para asegurar que un problema de valor inicial (PVI) tenga una única solución, se considera el
siguiente
Para que la solución sea única se puede exigir que la función cumpla la
En este apartado se estudiarán los métodos de Runge-Kutta de un solo paso, donde la solución aproximada se obtiene progresivamente de un punto al siguiente a partir de la información de la derivada en puntos intermedios dentro de cada intervalo, sin emplear los valores de pasos previos. Así, dado el problema
$$y'\left( t \right) = f\left( {t,y\left( t \right)} \right)\,\,\,\,\,\,\,\,\,t \in \left[ {{t_o},{t_f}} \right] $$la integración numérica del problema consiste en determinar unos instantes
$${t_o} < {t_1} < {t_2} < ... < {t_N} = {t_f} \,\,\,\,\,\,h_n=t_{n+1}-t_n$$y valores $$\left\{ {{y_o},\,\,{y_1},\,\,{y_2}, ...,\,\,{y_N}} \right\}$$ de forma que a partir de $$y\left( {{t_n}} \right) \approx {y_n}$$ se pueda obtener la aproximación de $y_{n+1}$.
En la imagen siguiente se muestra, para una ecuación diferencial ordinaria de primer orden, la solución analítica de un problema de valor inicial y la solución aproximada con 7 pasos considerando el intervalo $[0,4]$. El método numérico deberá indicar cómo obtener cada punto de la solución numérica a partir del anterior. En el caso del gráfico, el avance al siguiente punto utiliza la pendiente en el punto anterior.
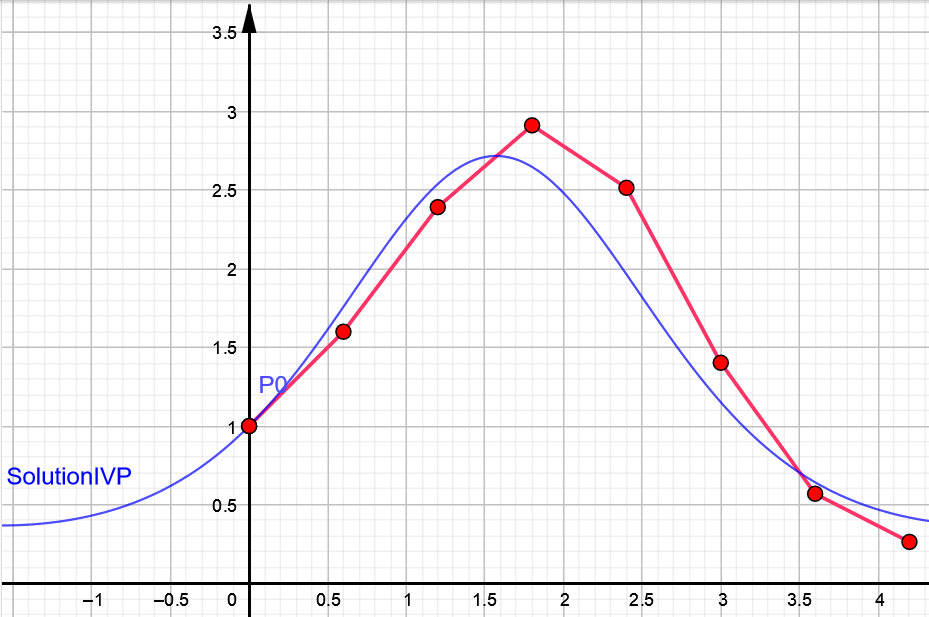
 Carl
David Tolmé Runge (30 de agosto de 1856 - 3 de enero de 1927) fue un matemático y físico
alemán conocido por su trabajo en análisis numérico y ecuaciones diferenciales. Nació en
Bremen, Alemania, y estudió matemáticas y física en las universidades de Múnich y Berlín,
obteniendo su doctorado en 1880. Runge es reconocido por desarrollar, junto con Martin
Kutta, los métodos de Runge-Kutta para resolver ecuaciones diferenciales ordinarias de
manera numérica. También realizó importantes contribuciones a la espectroscopía y la teoría
de aproximación. Fue profesor en la Universidad de Hannover y, más tarde, en la Universidad
de Gotinga.
Carl
David Tolmé Runge (30 de agosto de 1856 - 3 de enero de 1927) fue un matemático y físico
alemán conocido por su trabajo en análisis numérico y ecuaciones diferenciales. Nació en
Bremen, Alemania, y estudió matemáticas y física en las universidades de Múnich y Berlín,
obteniendo su doctorado en 1880. Runge es reconocido por desarrollar, junto con Martin
Kutta, los métodos de Runge-Kutta para resolver ecuaciones diferenciales ordinarias de
manera numérica. También realizó importantes contribuciones a la espectroscopía y la teoría
de aproximación. Fue profesor en la Universidad de Hannover y, más tarde, en la Universidad
de Gotinga.
 Martin
Wilhelm Kutta (3 de noviembre de 1867 - 25 de diciembre de 1944) fue un matemático alemán
conocido principalmente por su trabajo conjunto con Carl Runge en el desarrollo de los
métodos de Runge-Kutta para la solución numérica de ecuaciones diferenciales ordinarias.
Nacido en Pitschen (entonces parte de Prusia), estudió en las universidades de Breslavia y
Múnich, donde trabajó con destacados matemáticos de la época. Además de su contribución a
los métodos de Runge-Kutta, Kutta realizó estudios en mecánica y aerodinámica, desarrollando
la teoría de sustentación conocida como el "teorema de Kutta-Joukowski". Fue profesor en la
Universidad Técnica de Stuttgart., una familia de métodos numéricos ampliamente utilizados para resolver problemas de valor inicial en ecuaciones diferenciales ordinarias.
Martin
Wilhelm Kutta (3 de noviembre de 1867 - 25 de diciembre de 1944) fue un matemático alemán
conocido principalmente por su trabajo conjunto con Carl Runge en el desarrollo de los
métodos de Runge-Kutta para la solución numérica de ecuaciones diferenciales ordinarias.
Nacido en Pitschen (entonces parte de Prusia), estudió en las universidades de Breslavia y
Múnich, donde trabajó con destacados matemáticos de la época. Además de su contribución a
los métodos de Runge-Kutta, Kutta realizó estudios en mecánica y aerodinámica, desarrollando
la teoría de sustentación conocida como el "teorema de Kutta-Joukowski". Fue profesor en la
Universidad Técnica de Stuttgart., una familia de métodos numéricos ampliamente utilizados para resolver problemas de valor inicial en ecuaciones diferenciales ordinarias.
Su idea principal es aproximar la solución mediante una combinación ponderada de evaluaciones de la función derivada en puntos intermedios dentro de un intervalo. Estas evaluaciones permiten calcular el siguiente valor de la solución con más exactitud, sin necesidad de derivadas superiores.
El método de Euler
 Leonhard Euler (1707–1783), nacido en Basilea, Suiza, es considerado uno de los matemáticos más influyentes de la historia. Sus aportaciones en cálculo infinitesimal, análisis matemático, teoría de números y mecánica sentaron las bases para el desarrollo de múltiples disciplinas científicas.
es el procedimiento más sencillo para aproximar la solución de un problema de
valor inicial. Se analiza cómo obtener a partir de $y(t_n) \approx y_n$ el valor $y_{n+1}$. Dado que, $${y(t_{n + 1})} = {y(t_n)} +\color{blue}{ \int\limits_{{t_n}}^{{t_{n + 1}}} {f\left(
{t,y\left( t \right)} \right)dt}}$$
Leonhard Euler (1707–1783), nacido en Basilea, Suiza, es considerado uno de los matemáticos más influyentes de la historia. Sus aportaciones en cálculo infinitesimal, análisis matemático, teoría de números y mecánica sentaron las bases para el desarrollo de múltiples disciplinas científicas.
es el procedimiento más sencillo para aproximar la solución de un problema de
valor inicial. Se analiza cómo obtener a partir de $y(t_n) \approx y_n$ el valor $y_{n+1}$. Dado que, $${y(t_{n + 1})} = {y(t_n)} +\color{blue}{ \int\limits_{{t_n}}^{{t_{n + 1}}} {f\left(
{t,y\left( t \right)} \right)dt}}$$
se puede usar la fórmula de cuadratura con un nodo para obtener un valor aproximado de la integral de la forma siguiente
$${y(t_{n + 1})} \approx {y_{n+1}}={y_n} + \color{blue}{{h_n}f\left( {{t_n},{y_n}} \right)}$$La idea básica por tanto consiste en avanzar desde un valor conocido paso a paso, utilizando la pendiente de la función para estimar el siguiente valor.
En la siguiente figura se muestra gráficamente cómo obtener para un paso constante $h=1$ el punto $(t_1,y_1)$ a partir de $(t_0,y_0)$ y $(t_2,y_2)$ a partir de $(t_1,y_1)$ conocidas las derivadas en estos dos puntos.
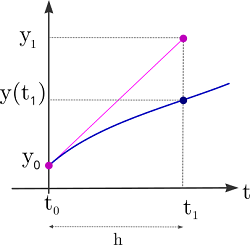
En este caso, $f(t,y)=0.7y-t^2+1$, el intervalo es $[1,2]$ y la condición inicial es $y(1)=1$.
Se calculan los cuatro primeros pasos de la aproximación de la curva solución del PVI. Se tiene $t_0=1$, $y_0=y(1)=1$.
$${t_1} = 1.1 \,\,\,\,\,\,\,\, y\left( {1.1} \right) \approx {y_1} = y_0 + 0.1 \cdot \,f\left( {1,\,\,y_0} \right) \approx 1.07$$ $${t_2} = 1.2 \,\,\,\,\,\,\,\, y\left( {1.2} \right) \approx {y_2} = y_1 + 0.1\, \cdot f\left( 1.1,\,\,y_1 \right) \approx 1.1239$$ $${t_3} = 1.3 \,\,\,\,\,\,\,\, y\left( {1.3} \right) \approx {y_3} = y_2 + 0.1 \cdot \,f\left( {1.2,\,\,y_2} \right) \approx 1.15857$$ $${t_4} = 1.4 \,\,\,\,\,\,\,\, y\left( {1.4} \right) \approx y_4=y_3 + 0.1\, \cdot f\left( {1.3,\,\,y_3} \right) \approx 1.17067$$ $$...$$Nótese que en cada paso se necesita el valor $y(t_n)$, por lo que cuanto más cercano sea el valor $y_n$ al real, $y(t_n)$, más preciso será el método. Así, para calcular $y_1$ se utiliza el valor $y_0$, para calcular $y_2$ se sustituye el valor exacto $y(t_1)$ desconocido por su valor aproximado $y_1$, para calcular $y_3$, se sustituye el valor $y(t_2)$ por su valor aproximado $y_2$, y así sucesivamente.
Se muestra seguidamente el código Matlab para obtener los cálculos de la solución aproximada del PVI anterior con 10 pasos.
clear all
f=@(t,y) 0.7*y-t.^2+1; %Función
a=1;b=2;y0=1; %Intervalo
N=10; %Pasos (N+1 puntos)
h=(b-a)/N; %Longitud del paso
t(1)=a;y(1)=y0;
for n=1:N
t(n+1)=t(n)+h;
% dy/dt=f(t,y)
y(n+1)=y(n)+h*f(t(n),y(n));
end
[t' y']
| t | 1 | 1.1 | 1.2 | 1.3 | 1.4 |
|---|---|---|---|---|---|
| y | 1.00000000 | 1.07000000 | 1.12390000 | 1.15857300 | 1.17067311 |
| t | 1.5 | 1.6 | 1.7 |
|---|---|---|---|
| y | 1.1566202277 | 1.112583643639000 | 1.034464498693729 |
| t | 1.8 | 1.9 | 2.0 |
|---|---|---|---|
| y | 0.917877013602290 | 0.758128404554450 | 0.550197392873262 |
Para dibujar tanto los valores obtenidos como la solución exacta en una misma gráfica en Matlab, se añadiría al código anterior el siguiente.
%Representación de los valores aproximados obtenidos
plot(t,y,'o')
xlabel(['Metodo de Euler con N=',num2str(N),' pasos'])
hold on
%Solución simbólica dada por Matlab
%Se define la función en simbólico
syms s(u)
%Se define la ecuación diferencial
eqn=diff(s)==f(u,s)
%Se define la condición inicial
cond=s(a)==y0
%Se resuelve con el comando dsolve
sol(u)=dsolve(eqn,cond)
%Representación de la solucion exacta
t1=linspace(a,b,50);
plot(t1,sol(t1))
hold off
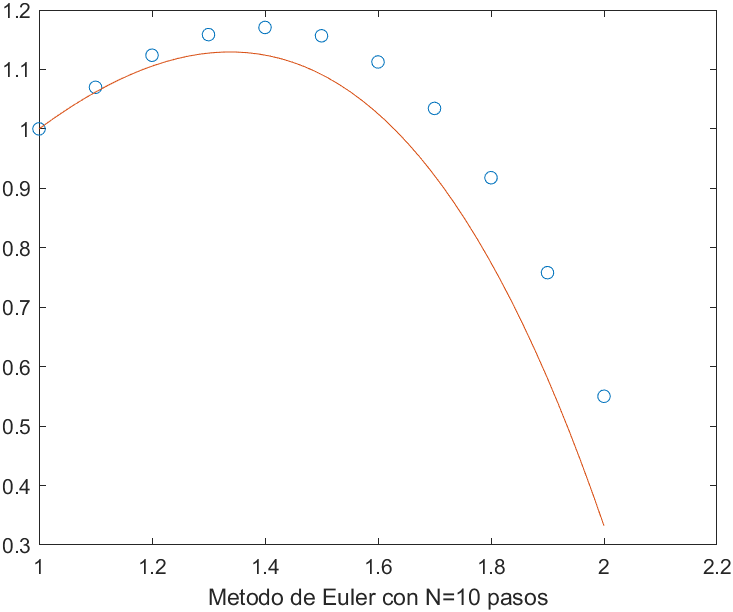
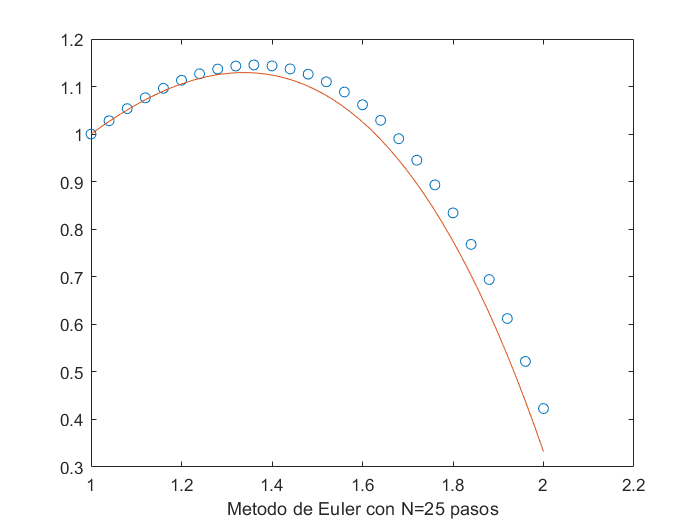
En forma general, se puede escribir el problema,
$$\begin{array}{l}{y_1} = \theta \,\,\,\,\,\,\,\,\,\,\,\,\,{y_2} = \theta '\\y = \left( {\begin{array}{ccccccccccccccc}{y{'_1}}\\{y{'_2}}\end{array}} \right) = \left( {\begin{array}{ccccccccccccccc}{{y_2}}\\{ - \frac{g}{L}sen\left( {{y_1}} \right)}\end{array}} \right)\,\,\,\,\,\,\,y\left( 0 \right) = \left( {\begin{array}{ccccccccccccccc}{{y_1}\left( 0 \right)}\\{{y_2}\left( 0 \right)}\end{array}} \right) = \left( {\begin{array}{ccccccccccccccc}{\frac{\pi }{6}}\\{ - 4}\end{array}} \right)\end{array}$$Escribiendo el cálculo con tres cifras decimales, se tendrá
$y\left( {0.5} \right) = y\left( 0 \right) + hf\left( {0,y\left( 0 \right)} \right)$ $$y\left( {0.5} \right) = \left( {\begin{array}{ccccccccccccccc}{\frac{\pi }{6}}\\{ - 4}\end{array}} \right) + h\left( {\begin{array}{ccccccccccccccc}{ - 4}\\{ - 9.81sen\left( {\frac{\pi }{6}} \right)}\end{array}} \right) = \left( {\begin{array}{ccccccccccccccc}{ - 1.476}\\{ - 6.452}\end{array}} \right)$$ $y\left( {1} \right) = y\left( 0.5 \right) + hf\left( {0.5,y\left( 0.5 \right)} \right)$ $$y\left( 1 \right) = \left( {\begin{array}{ccccccccccccccc}{ - 1.476}\\{ - 6.452}\end{array}} \right) + h\left( {\begin{array}{ccccccccccccccc}{ - 6.452}\\{ - 9.81sen\left( { - 1.476} \right)}\end{array}} \right) = \left( {\begin{array}{ccccccccccccccc}{ - 4.703}\\{ - 1.569}\end{array}} \right)$$
f=@(t,y) [y(2);-9.81*sin(y(1))]
y0=[pi/6;-4];h=0.5;t0=0;
%Valor en 0.5
y1=y0+h*f(t0,y0)
%Valor en 1
t1=t0+h; y2=y1+h*f(t1,y1) %Posición -4.703 rad, velocidad -1569 rad/s
Se calcula la deflexión para $1.5$ utilizando el método de Euler con un paso $h=0.1$, dando por tanto $N=15$ pasos.
Aplicando el método de Euler con $N$ pasos, se tendrá que $h=0.6/N$. El método de Euler, $y(n+1)=y(n)+hf(t(n),y(n))$, aplicado a cada componente de $y$ será
\[\begin{align} & {{y}_{1}}\left( n+1 \right)={{y}_{1}}\left( n \right)+h\,{{y}_{2}}\left( n \right) \nonumber\\ & {{y}_{2}}\left( n+1 \right)={{y}_{2}}\left( n \right)+h\,\left[ \frac{z\left( n \right)}{6.25\cdot {{10}^{4}}\left( 5+z\left( n \right) \right)}{{e}^{-\frac{z\left( n \right)}{15}}}{{\left( 30-z\left( n \right) \right)}^{2}} \right] \nonumber\\ & z\left( n+1 \right)=z\left( n \right)+h \nonumber \\ \end{align}\]En el código, se trabaja vectorialmente teniendo en cuenta que tanto $y$ como $f$ son vectores adaptando el código del ejemplo 6.4.
clear all
%Definición de la función
f=@(z,y) [y(2);z.*exp(-z/15)*10^-4.*(30-z).^2./(6.25*(5+z))]
h=0.1; % Longitud del paso
N=15; % Número de pasos
format long
z(1)=0;
y(:,1)=[0;0];
for n=1:N
z(n+1)=z(n)+h;
y(:,n+1)=y(:,n)+h*f(z(n),y(:,n));
end
%Resultados
[z' y(1,:)' y(2,:)']
%Representación de la solución
plot(z,y,'*')
legend('y1 aprox', 'y2 aprox')
La deflexión para 1.5 es $y(16)=0.001052773045811$ y su velocidad es $0.002241031532091$.
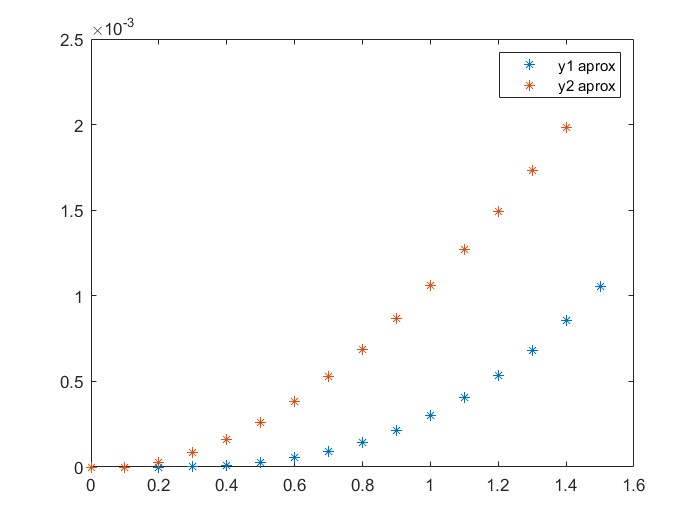
Las ecuaciones a resolver son las siguientes,
$$\begin{array}{l}\theta _1^{''} + 3\theta _1^{} - 2\theta _2^{} = 0\\2\theta _2^{''} - 2\theta _1^{} + 2\theta _2^{} = 0\end{array}$$Considerando $y_1=\theta_1$, $y_2=\theta_2$, $y_3=\theta_1^{'}$, $y_4=\theta_2^{'}$, el sistema a resolver es:
$$\left( {\begin{array}{ccccccccccccccc}{y{'_1}}\\{y{'_2}}\\{y{'_3}}\\{y{'_4}}\end{array}} \right) = \left( {\begin{array}{ccccccccccccccc}{{y_3}}\\{{y_4}}\\{ - 3{y_1} + 2{y_2}}\\{ {y_1} - {y_2}}\end{array}} \right)\,\,\,\,\,\,\,\,\,\left( {\begin{array}{ccccccccccccccc}{{y_1}\left( 0 \right)}\\{{y_2}\left( 0 \right)}\\{{y_3}\left( 0 \right)}\\{{y_4}\left( 0 \right)}\end{array}} \right) = \left( {\begin{array}{ccccccccccccccc}{0.1}\\{0.2}\\0\\0\end{array}} \right)$$Aplicando el método de Euler con $N$ pasos, se tendrá que $h=0.6/N$. El método de Euler, $y(n+1)=y(n)+hf(t(n),y(n))$, aplicado a cada componente de $y$ será
\[\begin{align} & {{y}_{1}}\left( n+1 \right)={{y}_{1}}\left( n \right)+h\,{{y}_{3}}\left( n \right) \nonumber \\ & {{y}_{2}}\left( n+1 \right)={{y}_{2}}\left( n \right)+h\,{{y}_{4}}\left( n \right) \nonumber \\ & {{y}_{3}}\left( n+1 \right)={{y}_{3}}\left( n \right)+h\,\left( -3{{y}_{1}}\left( n \right)+2{{y}_{2}}\left( n \right) \right) \nonumber\\ & {{y}_{4}}\left( n+1 \right)={{y}_{4}}\left( n \right)+h\,\left( {{y}_{1}}\left( n \right)-{{y}_{2}}\left( n \right) \right) \nonumber\\ & t\left( n+1 \right)=t\left( n \right)+h \nonumber\\ \end{align}\] En el código, se trabaja vectorialmente teniendo en cuenta que tanto $y$ como $f$ son vectores. Se definen los datos del problema.
clear all
%Definición de la función
f=@(t,y) [y(3);y(4);-3*y(1)+2*y(2);y(1)-y(2)]
h=0.1; %Longitud del paso
N=6; %Número de pasos
format long
t(1)=0;
y(:,1)=[0.1;0.2;0;0];
Se calculan los distintos pasos para obtener la solución aproximada.
for n=1:N
t(n+1)=t(n)+h;
y(:,n+1)=y(:,n)+h*f(t(n),y(:,n));
end
%Resultados
[t' y(1,:)' y(2,:)' y(3,:)' y(4,:)']
%Representación de la solución
plot(t,y,'*')
legend('theta1 aprox', 'theta2 aprox', 'theta1'' aprox', 'theta2'' aprox')
Se muestra a continuación los datos obtenidos en una tabla teniendo en cuenta que las componentes primera, segunda, tercera y cuarta de $y$ representan, respectivamente, $\theta_1$, $\theta_2$, $\theta'_1$ y $\theta'_2$
| t | $\theta_1$ | $\theta_2$ | $\theta'_1$ | $\theta'_2$ |
|---|---|---|---|---|
| 0 | 0.1 | 0.2 | 0 | 0 |
| 0.1 | 0.10000000 | 0.20000000 | 0.01000000 | -0.01000000 |
| 0.2 | 0.10100000 | 0.19900000 | 0.02000000 | -0.02000000 |
| 0.3 | 0.10300000 | 0.19700000 | 0.02950000 | -0.02980000 |
| 0.4 | 0.10595000 | 0.19402000 | 0.03800000 | -0.03920000 |
| 0.5 | 0.10975000 | 0.19010000 | 0.04501900 | -0.04800700 |
| 0.6 | 0.11425190 | 0.18529930 | 0.05011400 | -0.05604200 |
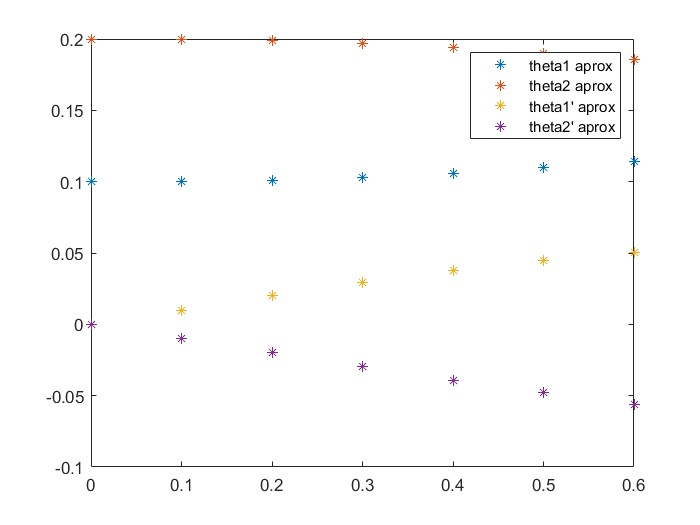
El interactivo muestra cómo evoluciona la aproximación de la solución (en azul) al aumentar el número de pasos, y permite ajustar tanto la EDO como las condiciones iniciales.
Para mejorar la precisión frente al esquema de Euler explícito, se puede recurrir a una regla de cuadratura que incorpore información en ambos extremos del intervalo como es el método de Heun
 Carl Friedrich Heun (1859-1932) fue un matemático alemán conocido por sus estudios sobre ecuaciones diferenciales de segundo orden y por desarrollar las funciones de Heun, que generalizan las funciones hipergeométricas. Su trabajo tiene aplicaciones en física teórica, especialmente en mecánica cuántica y relatividad..
Carl Friedrich Heun (1859-1932) fue un matemático alemán conocido por sus estudios sobre ecuaciones diferenciales de segundo orden y por desarrollar las funciones de Heun, que generalizan las funciones hipergeométricas. Su trabajo tiene aplicaciones en física teórica, especialmente en mecánica cuántica y relatividad..
Partiendo de la igualdad exacta
$${y(t_{n + 1})} = {y(t_n)} +\color{blue}{ \int\limits_{{t_n}}^{{t_{n + 1}}} {f\left( {t,y\left( t \right)} \right)dt}}$$se aproxima la integral mediante la regla del trapecio que para una función $g$ se expresa
$$\int\limits_{{t_n}}^{{t_n} + {h_n}} {g\left( t \right)dt} \approx {{{h_n}} \over 2}\left( {g\left( {{t_{_n}}} \right) + g\left( {{t_{n + 1}}} \right)} \right)$$Si se toma $g(t)=f(t,y(t))$ y se sustituye ${y_n} \approx y\left( {{t_n}} \right)$, se obtiene
$${y_{n + 1}} = {y_n} + {{{h_n}} \over 2}\left[ {f\left( {{t_n},{y_n}} \right) + f\left( {{t_{n + 1}},\color{red}{{y(t_{n + 1})}}} \right)} \right]$$ Como $y(t_{n+1})$ aparece en el término derecho, se reemplaza por su predicción por Euler $${y_{n + 1}} = {y_n} + {{{h_n}} \over 2}\left[ {f\left( {{t_n},{y_n}} \right) + f\left( {{t_n} + {h_n},\color{red}{\underbrace {{y_n} + {h_n}f\left( {{t_n},{y_n}} \right)}_{Euler}}} \right)} \right]$$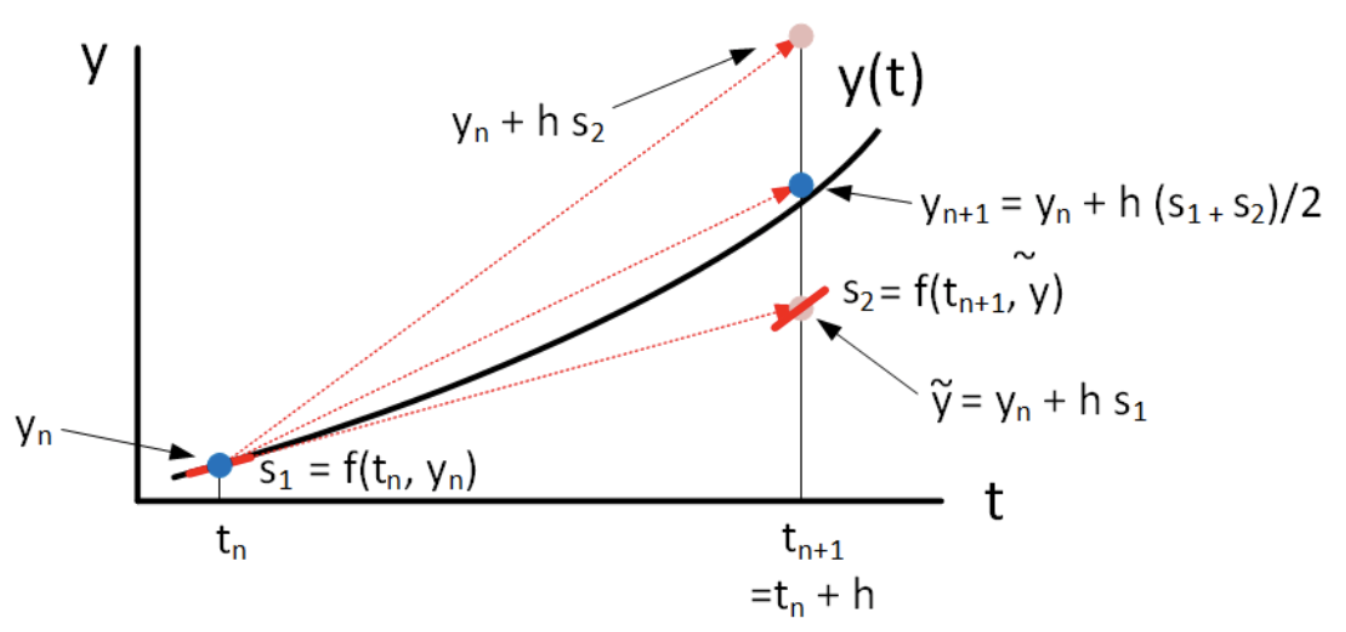
Tomando un paso $h=0.8$, obtener el valor aproximado de $y(1.8)$ utilizando el método de Heun.
En este caso se tiene que $f(t,y)=t-y$, $t_0=1$ e $y_0=0.5$. Tomando $h=0.8$, en el punto $t=1.8$ la solución aproximada se obtendrá como el promedio entre la pendiente en el punto inicial $(1, 0.5)$ y el previsto por el método de Euler para $t=1.8$.
asociando este algoritmo al siguiente tablero
$$\begin{array} {r|r r } 0 & 0 & 0 \\ \color{red}{1} & \color{green}{1} & 0 \\ \hline & \color{blue} {1/2} & \color{blue} {1/2} \\ \end{array}$$A continuación se muestra el código Matlab para calcular los pasos del método de Heun.
clear all
f=@(t,y) (t-y)/2 %Función
t0=0;tf=3; %Intervalo
N=30; %Número de Pasos
h=(tf-t0)/N; %Longitud del paso
%Condición inicial
t(1)=t0;y(1)=1;
%Se realizan N pasos
for n=1:N
t(n+1)=t(n)+h;
%Método de Heun
k1=f(t(n),y(n));
k2=f(t(n)+h,y(n)+h*k1);
y(n+1)=y(n)+(k1+k2)*h/2;
end
%Se representan los valores obtenidos
plot(t,y,'*')
%Se representa la solución exacta
hold on
t1=linspace(t0,tf,50);
plot(t1,3*exp(-t1/2)-2+t1)
hold off
%Se comparan los valores obtenidos entre
%la solución exacta y la obtenida
yexac=3*exp(-t/2)-2+t;
[y' yexac' (y-yexac)']
Llamando $y_1=y$, $y_2=y'$, se tiene
$$\begin{aligned} &{y'_1} = {y_2} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, {y'_2} = - 7seny - 0.1\cos t \\ &{y_1}\left( 0 \right) = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,{y_2}\left( 0 \right) = 1 \end{aligned} $$En este caso,
$$ \left( \begin{aligned} {{y'_1}\left( t \right)} \\ {{y'_2}\left( t \right)} \\ \end{aligned} \right)=\left( \begin{aligned} {{y_2}} \\ {-7sen({y_1})-0.1cos(t)} \\ \end{aligned} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \left( \begin{aligned} {{y_1}\left( 0 \right)} \\ {{y_2}\left( 0 \right)} \\ \end{aligned} \right)=\left( \begin{aligned} {{0}} \\ {1} \\ \end{aligned} \right)$$El código para resolver la EDO aplicando el método de Heun con matlab considerando $N=30$ pasos se muestra a continuación.
clear all
%Función
f=@(t,y) [y(2);-7*sin(y(1))-0.1*cos(t)]
t0=0;tf=5;%Intervalo
N=30;%Pasos
h=(tf-t0)/N; %Longitud del paso
%Condición inicial
t(1)=t0;y0=[0;1];y(:,1)=y0;
for n=1:N %
t(n+1)=t(n)+h;
k1=f(t(n),y(:,n));
k2=f(t(n)+h,y(:,n)+h*k1);
y(:,n+1)=y(:,n)+(k1+k2)*h/2;
end
%Representación de la solución aproximada obtenida
plot(t,y,'*')
hold on
legend('y_1','y_2')
xlabel(['Metodo de Heun con N=',num2str(N),' pasos'])
En la primera componente de la solución está la aproximación de $y(t)$, en la segunda, la aproximación de la derivada.
Dado el PVI siguiente
$$\begin{aligned} & y'\left( t \right) = f\left( {t,y\left( t \right)} \right)\,\,\,\,\,\,\,\,\,t \in \left[ {{t_o},{t_f}} \right] \\ & y\left( {{t_o}} \right) = {y_0} \end{aligned} $$ se muestra cómo calcular, $y(t_{n+1})$ a partir de $y(t_n)$. Para ello, se considera la siguiente igualdad $$y\left( {{t_{n + 1}}} \right) = y\left( {{t_n}} \right)\, + \int\limits_{{t_n}}^{{t_n+h_n}} {y'\left( t \right)dt} $$En la imagen se representa un ejemplo con $m=6$ donde se muestran los valores $\color{red}{c_i}$ y $t_{n,i}$.

En la expresión anterior se observa que se precisa también calcular una aproximación de los valores $y(t_n+{\color{red}{c_i}}h_n)$. Considerando de nuevo la siguiente igualdad
$$y_{n,i} = y\left( t_n + {\color{red}{c_i}} h_n \right) = y\left( t_n \right) + \int\limits_{t_n}^{t_n + {\color{red} {c_i}} h_n} f\left( t,y\left( t \right) \right)dt $$y utilizando alguna fórmula de cuadratura de $m$ pasos, se puede obtener una aproximación en estos puntos
$$y\left( t_n + {\color{red}{c_i}} h_n \right) \approx y_n + {h_n}\sum\limits_{j = 1}^m {\color{green}{a_{ij}}} {\underbrace {f(t_n + {\color{red}{c_j}} h_n, y_{n,j})}_{{K_{n,j}}} } $$Cuando los métodos son explícitos, la matriz $A$ es triangular inferior. Los métodos de Runge-Kutta pueden describirse a trávés del llamado
 John
Charles Butcher (nacido en 1933 en Auckland, Nueva Zelanda) es un matemático reconocido por
sus contribuciones a los métodos numéricos para ecuaciones diferenciales, en particular los
métodos de Runge-Kutta y el "Butcher tableau". Estudió en el Auckland University College y
la Universidad de Sídney, donde obtuvo su Ph.D. en 1961. En 2013, fue nombrado Oficial de la
Orden del Mérito de Nueva Zelanda por sus servicios a las matemáticas.
donde se pueden disponer los parámetros $A$, $b$ y $c$ de la forma siguiente:
John
Charles Butcher (nacido en 1933 en Auckland, Nueva Zelanda) es un matemático reconocido por
sus contribuciones a los métodos numéricos para ecuaciones diferenciales, en particular los
métodos de Runge-Kutta y el "Butcher tableau". Estudió en el Auckland University College y
la Universidad de Sídney, donde obtuvo su Ph.D. en 1961. En 2013, fue nombrado Oficial de la
Orden del Mérito de Nueva Zelanda por sus servicios a las matemáticas.
donde se pueden disponer los parámetros $A$, $b$ y $c$ de la forma siguiente:
Si se consideran el esquema explícito y el paso de longitud constante $h$, el método para obtener $y_{n+1}$ a partir de $y_n$ puede escribirse también de la forma siguiente,
$$ \begin{aligned} &\,\,\,\,\,\,\,\,\,{K_{1}} = f\left( {{t_{n}},{y_{n}}} \right)\\ &\,\,\,\,\,\,\,\,\, {K_{i}} = f\left( {t_n} + {\color{red} {c_i}} {h},y_n+{h} \sum\limits_{j = 1}^{m} {\color{green}{a_{ij}}} {K_{j}} \right) \,\,\,\,\,\,2 \le i \le m\\ &{y_{n + 1}} = {y_n} + {h}\sum\limits_{j = 1}^m {\color{blue}{b_j}}{K_{j}}\ \end{aligned} $$El método dado por el tablero se corresponde con el siguiente algoritmo
$$\begin{aligned} & K_1=f(t_n,y_n)\\ & K_2=f(t_n+{\color{red}{\frac{1}{2}}} h,y_n+{\color{green}{\frac{1}{2}}} h K_1)\\ & K_3=f(t_n+{\color{red}{\frac{3}{4}}} h,y_n+{\color{green}{\frac{3}{4}}} h K_2)\\ \end{aligned}$$ $$y_{n+1}=y_n+\frac{h}{{\color{blue}{9}}}({\color{blue}{2}} K_1+{\color{blue}{3}} K_2+{\color{blue}{4}} K_3)$$Para aproximar la solución del PVI del enunciado en $t=0.4$, partiendo de $t_0=0$ e $y_0=0$ con paso $h=0.2$, siendo $f(t,y)=t+e^y$, se deben realizar dos pasos.
Con el siguiente código Matlab/Octave se pueden realizar los cálculos. Al precisar dos pasos, se escribe cada paso directamente.
%Definición de la función
f=@(t,y) t+exp(y)
%Valores
h=0.2;t0=0;y0=0;
%Paso 1
K1=f(t0,y0)
K2=f(t0+h/2,y0+h/2*K1)
K3=f(t0+3*h/4,y0+3*h/4*K2)
y1=y0+h/9*(2*K1+3*K2+4*K3)
%Paso 2
t1=t0+h;
K1=f(t1,y1)
K2=f(t1+h/2,y1+h/2*K1)
k3=f(t1+3*h/4,y1+3*h/4*K2)
y2=y1+h/9*(2*K1+3*K2+4*k3)
clear all
%Definición función
f=@(t,y) 0.7*y-t.^2+1;
%Definición intervalo
t0=1;tf=2;%Intervalo
N=5;%Pasos (N+1 puntos)
h=(tf-t0)/N; %Longitud del paso
t(1)=t0;y0=1;y(1)=y0;
for n=1:N
k1=f(t(n),y(n));
k2=f(t(n)+h/2,y(n)+h*k1/2);
k3=f(t(n)+h*3/4,y(n)+h*k2*3/4);
y(n+1)=y(n)+(2*k1+3*k2+4*k3)*h/9;
t(n+1)=t(n)+h;
end
%Se representa la solución obtenida
plot(t,y,'*')
legend('y')
xlabel(['Metodo con tablero y N=',num2str(N),' pasos'])
hold on
%Se representa la solución dada por Matlab/Octave
%con el comando numérico ode45
[t,sol]=ode45(f,[t0,tf],y0);
plot(t,sol)
legend('y')
hold off
[t,x] = ode45(odefun, tinter, x0). Donde odefun es la función que define la EDO, tinter es el intervalo de tiempo y x0 son las condiciones iniciales.
En este caso la EDO es de orden 3. Llamando $y_1=y$, $y_2=y'$, el problema de valor inicial se escribirá
Llamando $y_1=y$, $y_2=y'$, $y_3=y''$, se tiene
$${y'_1} = {y_2}\,\,\,\,\,\,\,\,\,\,{y'_2} = {y_3}\,\,\,\,\,\,\,\,\,\,y'_3 = 4{y_2} + t + 3\cos \left( t \right){\mkern 1mu} {\mkern 1mu} + {e^{ - 2t}}$$ $${y_1}\left( 0 \right) = 2\,\,\,\,\,\,\,\,\,\,{y_2}\left( 0 \right) = - 23/40\,\,\,\,\,\,\,\,\,\,{y_3}\left( 0 \right) = 29/4$$En este caso,
$$ \left( \begin{aligned} {{y'_1}\left( t \right)} \\ {{y'_2}\left( t \right)} \\ {{y'_3}\left( t \right)} \\ \end{aligned} \right)=\left( \begin{aligned} {{y_2}} \\ {{y_3}} \\ {4{y_2} + t + 3\cos \left( t \right){\mkern 1mu} {\mkern 1mu} + {e^{ - 2t}}} \\ \end{aligned} \right)\,\,\,,\,\,\,\,\ \left( \begin{aligned} {{y_1}\left( 0 \right)} \\ {{y_2}\left( 0 \right)} \\ {{y_3}\left( 0 \right)} \\ \end{aligned} \right)=\left( \begin{aligned} {{2}} \\ {-23/40} \\{29/40} \\ \end{aligned} \right)$$ Trabajando en forma vectorial, la primera componente de $y$ es la solución del PVI, la segunda es la derivada primera y la tercera es la segunda derivada de la solución. El código Matlab/Octave a utilizar es el siguiente.
clear all
%Definición función
f=@(t,y) [y(2);y(3);4*y(2)+t+3*cos(t)+exp(-2*t)];
%Definición intervalo
t0=0;tf=1;%Intervalo
N=5;%Pasos (N+1 puntos)
h=(tf-t0)/N; %Longitud del paso
t(1)=t0;y0=[2;-23/40;29/4];
y(:,1)=y0;
for n=1:N
k1=f(t(n),y(:,n));
k2=f(t(n)+h/2,y(:,n)+h*k1/2);
k3=f(t(n)+h*3/4,y(:,n)+h*k2*3/4);
y(:,n+1)=y(:,n)+(2*k1+3*k2+4*k3)*h/9;
t(n+1)=t(n)+h;
end
plot(t,y,'*')
legend('y_1','y_2','y_3')
xlabel(['Metodo con tablero y N=',num2str(N),' pasos'])
hold on
%Se compara con la solución numérica dada con ode45
[t,sol]=ode45(f,[t0,tf],y0);
plot(t,sol)
legend('y_1','y_2','y_3')
hold off
En la siguiente imagen se muestra la solución obtenida con la solución dada por Matlab/Octave.
En este apartado se mostrarán algunos métodos de Runge -Kutta con su tablero de Butcher.
Método de Euler
$$\begin{array} {r|r } 0 & 0 \\ \hline & 1 \\ \end{array}$$Método de Heun
$$\begin{array} {r|r r } 0 & 0 & 0 \\ 1 & 1 & 0 \\ \hline & 1/2 & 1/2 \\ \end{array}$$Método de Kutta de Tres Etapas
$$\begin{array} {r|r r } 0 & 0 & 0 & 0 \\ {\color{red}{1/2}} & {\color{green}{1/2}} & 0 & 0 \\ {\color{red}{1}} & {\color{green}{-1}} & {\color{green}{2}} & 0 \\ \hline & {\color{blue}{1/6}} & {\color{blue}{4/6}} & {\color{blue}{1/6}} \\ \end{array}$$También podría escribirse de la forma siguiente.
Con el siguiente interactivo se pueden resolver EDOs de primer orden y comparar el resultado por distintos métodos de Runge-Kutta.
Se muestra a continuación ejemplos de aplicación de PVI resueltos con Matlab/Octave aplicando distintos métodos de Runge-Kutta.
Con los datos del problema, el PVI es,
$$\begin{array}{l}2\frac{{{d^2}x}}{{d{t^2}}} + 3\frac{{dx}}{{dt}} + 5x = sen\left( {2t} \right)\\x\left( 0 \right) = 1\,\,\,\,\,x'\left( 0 \right) = 0\end{array}$$Para escribir la EDO en su forma general, se considera $x_1=x$, $x_2=x'$ y se tendrá
Es decir,
$$\left( {\begin{array}{ccccccccccccccc}{x{'_1}}\\{x{'_2}}\end{array}} \right) = \left( {\begin{array}{ccccccccccccccc}{{x_2}}\\{ - \frac{3}{2}{x_2} - 5{x_1} + sen\left( {2t} \right)}\end{array}} \right)\,\,\,\,\,\,,\,\,\,\,\,\,\,\left( {\begin{array}{ccccccccccccccc}{{x_1}\left( 0 \right)}\\{{x_2}\left( 0 \right)}\end{array}} \right) = \left( {\begin{array}{ccccccccccccccc}0\\0\end{array}} \right)$$Utilizando el método de Euler con paso $h=0.01$, se calcula en que instante aproximadamente se obtendrá que $x=0$.
clear all
%Definición función
f=@(t,x) [x(2);-3/2*x(2)-5/2*x(1)+sin(2*t)/2];
%Definición intervalo
t0=0;
h=0.01; %Longitud del paso
t(1)=t0;x0=[1;0];
x(:,1)=x0;n=1; pos=1;
while pos>0
t(n+1)=t(n)+h;
x(:,n+1)=x(:,n)+h*f(t(n),x(:,n));
pos=x(1,n+1);
n=n+1;
end
t(n) %Aproximadamente en 1.85 segundos
Para resolver la EDO utilizando el método de Runge-Kutta de orden 4 con $h=0.01$, se puede considerar el siguiente código Matlab/Octave.
t0=0;
h=0.01; %Longitud del paso
t(1)=t0;x0=[1;0];
x(:,1)=x0;N=200;
Se implementa el tablero para obtener por el método de Runge-Kutta la solución aproximada.
for n=1:N %
k1=f(t(n),x(:,n));
k2=f(t(n)+h/2,x(:,n)+h*k1/2);
k3=f(t(n)+h/2,x(:,n)+h*k2/2);
k4=f(t(n)+h,x(:,n)+h*k3);
x(:,n+1)=x(:,n)+(k1+2*k2+2*k3+k4)*h/6;
t(n+1)=t(n)+h;
end
plot(t,x,'*')
legend('sol aprox')
En este caso la EDO es de orden 1. Se tiene $f(t,y)=yt^3-1.5y$, $y(0)=1$. Como se pide considerar 9 pasos, se tendrá $h=1.8/9$.
clear all
f=@(t,y) y*t^3-1.5*y;%Función
t0=0;tf=1.8;%Intervalo
N=5;%Pasos (N+1 puntos)
h=(tf-t0)/N; %Longitud del paso
t(1)=t0;y0=1;y(1)=y0;
Se escribe el código Matlab/Octave para resolver el problema definiendo los valores $K_i$ correspondientes al tablero.
for n=1:N %
k1=f(t(n),y(n));
k2=f(t(n)+h/2,y(n)+h*k1/2);
k3=f(t(n)+h/2,y(n)+h*k2/2);
k4=f(t(n)+h,y(n)+h*k3);
y(n+1)=y(n)+(k1+2*k2+2*k3+k4)*h/6;
t(n+1)=t(n)+h;
end
plot(t,y,'*')
legend('sol aprox')
En este ejemplo, como se puede obtener la solución exacta que es la función $y(t)={e^{{{t\left( {{t^3} - 6} \right)} \over 4}}}$, se representa en una misma gráfica esta curva y la aproximación obtenida.
hold on
x=linspace(t0,tf,30);
plot(x,exp((x.^4-6*x)/4),'r')
legend('sol aprox','sol exacta')
hold off
En el siguiente ejemplo, se programa el método de Runge-Kutta construyendo los valores $K_i$ a partir de la definición de las matrices del tablero de Butcher asociado.
f=@(t,y) y*t^3-1.5*y;%Función
t0=0;tf=1.9;%Intervalo
N=5;%Pasos (N+1 puntos)
h=(tf-t0)/N; %Longitud del paso
%Condiciones iniciales
t(1)=t0;y0=1;y(1)=y0;
%Definición tablero
C=[0 1/2 1/2 1];
A=[0 0 0 0;1/2 0 0 0;0 1/2 0 0;0 0 1 0];
B=[1/6 2/6 2/6 1/6];
m=length(B);
for n=1:N %
%Construcción Ki con datos tablero en cada paso
kn=[f(t(n),y(n))];
for j=2:m
kn = [kn, f(t(n)+h*C(j),y(n)+h*kn*A(j,1:j-1)')];
end
%Aproximación en punto siguiente
y(n+1)=y(n)+h*kn*B';
t(n+1)=t(n)+h;
end
plot(t,y,'*')
%Solución exacta
hold on
x=linspace(t0,tf,30);
plot(x,exp((x.^4-6*x)/4),'r')
legend('sol aprox','sol exacta')
hold off
En el siguiente ejemplo, se resuelve un sistema de ecuaciones diferenciales utilizando el método de Runge-Kutta de cuarto orden.
donde $(y_1,y_2)$ son las coordenadas de uno de los cuerpos (satélite) en un sistema con origen en el otro cuerpo central. Los valores $(y_3,y_4)$ representan el vector velocidad del cuerpo satélite.
Utiliza el método de Runge-Kutta clásico para encontrar la solución con las condiciones iniciales siguientes
$$y_1(0) = 1,\,\,y_2(0) =1,\,\,\, y_3(0) = 0,\,\,\,y_4(0) = 1$$Se muestra a continuación el código Matlab/Octave para resolver el problema.
El tablero de Butcher para el método de Runge-Kutta clásico de cuarto orden es
$$\begin{array} {r|r r r r } 0 & 0 & 0 & 0 & 0 \\ 1/2 & 1/2 & 0 & 0 & 0 \\ 1/2 & 0 & 1/2 & 0 & 0 \\ 1 & 0 & 0 & 1 & 0 \\ \hline & 1/6 & 2/6 & 2/6 & 1/6\\ \end{array}$$
clear all
%Definición de la función
f=@(t,y) [y(3);y(4);-y(1)/(y(1)^2+y(2)^2)^(3/2);-y(2)/(y(1)^2+y(2)^2)^(3/2)];
%Datos PVI
t0=0;tf=8*pi;
y(:,1)=[1;1;0;1];h=0.1;N=ceil(tf/h);t(1)=t0;
for n=1:N
k1=f(t(n),y(:,n));
k2=f(t(n)+h/2,y(:,n)+h*k1/2);
k3=f(t(n)+h/2,y(:,n)+h*k2/2);
k4=f(t(n)+h,y(:,n)+h*k3);
y(:,n+1)=y(:,n)+(k1+2*k2+2*k3+k4)*h/6;
t(n+1)=t(n)+h;
end
%Representación de la solución
plot(y(1,:),y(2,:),'r')
axis equal
En la siguiente imagen se muestra la trayectoria del satélite una vez resuelto el problema.
pasorkf(f,tn,hn,yn,a,b,c)
f, tn, hn, yn, a, b, c que son respectivamente, la función $f$, $t(n)$, el paso $h$, $y(n)$ y los parámetros $A$, $b$ y $c$ del método de Runge-Kutta que se considere.
Utilizando estas funciones, el código Matlab/Octave para encontrar la solución se muestra a continuación.
%Definición de la función
f=@(t,y) [y(3);y(4);-y(1)/(y(1)^2+y(2)^2)^(3/2);-y(2)/(y(1)^2+y(2)^2)^(3/2)];
%Datos PVI
t0=0;tf=8*pi;
y0=[1;1;0;1];
y(1)=y0;t(1)=t0;
N=100;h=tf/N;
%Se definen el tablero
[a,b,c]=mirkf4c;
for iter=1:N
%Se ejecuta el paso utilizando la función pasokf.m
y(:,n+1)=pasorkf(f,t(n),h,y(:,n),a,b,c);
t(n+1)=t(n)+h;
end
%Representación de la solución
plot(y(1,:),y(2,:),'r')
axis equal
A continuación, se estudiará el error en los métodos de Runge–Kutta. Para ello, se comienza por observar que dichos métodos pueden expresarse de la siguiente forma:
$${y_{n + 1}} = {y_n} + {h_n}{\Phi _f}\left( {{t_n},{y_n},{h_n}} \right)\,\,\,\,\,\,\,0 \le n \le N - 1$$Se introduce el concepto de orden de un método numérico para ecuaciones diferenciales ordinarias para medir la rapidez con la que decrece el error global al reducir el tamaño del paso $h$. Se presentan los conceptos fundamentales para caracterizar este orden
El
El
Se puede observar que:
Para determinar el orden de un método de Runge-Kutta se emplean las
Los métodos vistos hasta este momento tienen una dependencia directa con el paso $h$
considerado, por lo que su elección puede condicionar enormemente el funcionamiento del propio
método. Se plantea en este apartado cómo determinar cuál es el paso de tiempo $h$ mas
indicado analizando los llamados
Estos métodos consisten en una variación del paso $h$ a partir del control de los errores de aproximacion obtenidos a medida que se calculan las diferentes iteraciones del método.
Así, si llegado el momento, el error de aproximación supera la tolerancia establecida para ́este, el método varía el paso para tener una mejor aproximacion. Por el contrario, si el error es menor que la tolerancia, el ḿetodo amplía el paso con el fin de acelerar el rendimiento.
Estos métodos emplean dos fórmulas de diferente orden, que comparten evaluaciones intermedias de la función derivada, para calcular dos aproximaciones del siguiente paso: una más precisa y otra menos precisa. La diferencia entre ambas proporciona una estimación del error, que puede usarse para ajustar automáticamente el tamaño del paso en los métodos de paso variable, optimizando el equilibrio entre precisión y número de operaciones a realizar para encontrar la solución.
donde las matrices $A$ y $c$ del método de orden $p$ están encajados en $\widehat A$ y $\widehat c$ del método de orden $q > p$.
Al ser el método de orden $q$ más preciso, el valor ${\varepsilon _n} = \left\| {{{\widetilde y}_{n + 1}} - {y_{n + 1}}} \right\|$ es una estimación del error local cometido por el primer método. No obstante, como ${\widehat y_{n + 1}}$ es mejor aproximación de la solución que $ y_{n + 1}$, entonces se tomará como aproximación ${\widehat y_{n + 1}}$ y la cantidad ${\varepsilon _n} = \left\| {{{\widetilde y}_{n + 1}} - {y_{n + 1}}} \right\|$ será una cota superior de la integración.
A modo de ejemplo, se verán los métodos de Fehlberg que son una familia de métodos de Runge–Kutta encajados que proporcionan dos aproximaciones de distinto orden. En este libro, se consideran únicamente los métodos de orden 4 y 5. Su esquema más conocido es el RKF45, usado ampliamente en librerías como ode45 de MATLAB.
En estos métodos los parametros $A$ y $c$ del esquema de orden 4 coinciden con las 5 primeras filas de $\widehat A$ y $\widehat c$ del esquema de orden 5. Por tanto, las etapas $K_{n,i}$ para $1 \le i \le 5$ son idénticas en ambos metodos, lo que reduce el número de evaluaciones de $f$.
Runge-Kutta-Felhberg 4-5 #1
Para pasar de $t_n$ a $t_{n+1}$ y hallar una cota del error local de aproximación de $y(t_{n+1})$, se aplica el método de orden 5 para obtener $\widehat y_{n+1}$ y el método de orden 4 para obtener $y_{n+1}$. La estimación del error será $\left\| {{{\widehat y}_{n + 1}} - {y_{n+1}}} \right\|$.
Además, si $${y_{n + 1}} = {y_n} + {h_n}\sum\limits_{j = 1}^m {{b_j}{K_{n,j}}} $$ $${\widehat y_{n + 1}} = {y_n} + {h_n}\sum\limits_{j = 1}^{\widehat m} {{{\widehat b}_j}{K_{n,j}}} \,\,\,\,\,\,\,\,\,\,\,\widehat m > m$$la estimación del error se puede obtener de la forma siguiente
$$\left\| {{{\widehat y}_{n + 1}} - {y_{n+1}}} \right\| = {h_n}\sum\limits_{j = 1}^{\widehat m} {\left( {{{\widehat b}_j} - {b_j}} \right){K_{n,j}}} $$
En consecuencia, basta conocer los parámetros del esquema de orden $q$ y el
La información que se precisa para el esquema Runge-Kutta-Felhberg 4-5 #1 se incluye en el siguiente tablero.
$$ {\begin{array} {r|r r r r r} 0 & & & & & \\ 2/9 & 2/9 & & & & \\ 1/3 & 1/12 & 1/4 & & & \\ 3/4 & 69/128 & -243/128 & 135/64 & & \\ 1 & -17/12 & 27/4 & -27/5 & 16/15 & \\ 5/6 & 65/432 & -5/16 & 13/16 & 4/27 & 5/144 & \\ \hline orden 5 & 47/450 & 0 & 12/25 & 32/225 & 1/30 & 6/25\\ estimadores & 1/150 & 0 & -3/100 & 16/75 & 1/20 & -6/25\\ \end{array}}$$La función rkf45a.m desarrollada por Eduardo Casas (ficheros Matlab) devuelve los valores $A$, $b$, $c$, $est$ para el par de métodos encajados de orden 4 y 5 del método de Runge-Kutta-Fehlberg #1.
Runge-Kutta-Felhberg 4-5 #2
El siguiente tablero describe otro método Runge-Kutta-Fehlberg donde se encajan también un esquema de orden 4 y otro de orden 5.
La función rkf45b.m desarrollada por Educardo Casas devuelve los valores $A$, $b$, $c$, $est$ para el par de métodos encajados de orden 4 y 5 del método de Runge-Kutta-Fehlberg #2.
Algoritmo esquemas Runge-Kutta encajados
A partir de dos métodos encajados de órdenes $p$ y $q$ con $p <q$, el algoritmo para cálcular un paso y los estimadores es el siguiente.
La función rkf.m, desarrollada por Eduardo Casas (ficheros Matlab), implementa un paso con la estimación del error. La sintáxis es la siguiente
[yn1,en]=rkf(f,tn,hn,yn,a,b,c,est);
Los parámetros de entrada son:
Los parámetros de salida son
A partir de la estimación del error, el método encajado ajusta dinámicamente el tamaño del paso basándose en un umbral de tolerancia. En cada iteración se calculan dos soluciones de distinto orden y, al comparar su diferencia (el estimador de error local) con un umbral que combina tolerancias absoluta y relativa, se decide si aceptar o rechazar el paso. Si el error queda dentro del umbral, se avanza; si no, se descarta la aproximación y se reduce el paso. Por último, se actualiza $h$ para asegurar que el siguiente paso cumpla la precisión requerida.
La tolerancia adaptativa deseada se define a partir del error absoluto $\varepsilon_a$ y el error relativo $\varepsilon_r$. Dado que el error de $q$ es menor que el de $p$, se considera para la tolerancia el del método de orden mayor
$$TOL=\varepsilon_a+\varepsilon_r||{\hat y_{n + 1}}||$$A continuación se muestra el control adaptativo del paso, que consiste en estimar el error local en cada iteración y ajustar automáticamente el siguiente paso para mantenerlo dentro de la tolerancia establecida.
Previsión del paso siguiente. Se calcula $r_n$ de la forma indicada en el punto 3 y se toma
A continuación se ilustra el proceso con varios ejemplos usando el método Runge–Kutta–Felhberg 4-5 #1.
Se considera $y_1(t)=y(t)$, $y_2(t)=z(t)$, $y_3(t)=y'(t)$, $y_4(t)=z'(t)$ y se incluye en el código Matlab/Octave los datos del problema.
format long
%Problema a resolver
f=@(t,y) [y(3);y(4);-y(1)./(y(1).^2+y(2).^2).^1.5;-y(3)./(y(1).^2+y(2).^2).^1.5];
t0=0;tf=20;y0=[0.5;0;0;sqrt(3)];
%Error absoluto y relativo
ea=10^-12;er=10^-10;
%Métodos encajados
[a b c est]=rkf45a;
Se define el paso inicial.
hmin=(tf-t0)/10^6;p1=0.2; % p1=1/(1+4) p=4 en RKF 4-5
hn=max(hmin,(ea+er*norm(y0))^p1);
Se comienza a iterar y se comprueba si la estimación del error es inferior a la tolerancia. Si se cumple, se avanza estableciendo el nuevo paso.
%Cálculo del paso con estimación error
tn=t0;yn=y0;t=[t0];y=[y0];
[yn1,en]=rkf(f,tn,hn,yn,a,b,c,est);
%Cálculo de la tolerancia
TOL=ea+er*norm(yn1);
if en<TOL
%Se acepta el paso
tn=tn+hn;yn=yn1;
t=[t tn];
y=[y yn];
%Se establece el nuevo paso
rn=0.9*(TOL/en)^p1;
if rn<1|rn>1.1
hn=min(rn,5)*hn;
end
else
disp('Fallo del paso ')
[en TOL]
end
Este bloque de código se itera hasta que se detecte un rechazo de paso, en cuyo caso se reduce su tamaño, o hasta haberse completado el intervalo de integración. Se modifica el código para detectar si se ha llegado al final del intervalo de integración.
fallo=0;
while (tn<=tf)&(fallo==0)
%Cálculo del paso con estimación error
[yn1,en]=rkf(f,tn,hn,yn,a,b,c,est);
%Cálculo de la tolerancia
TOL=ea+er*norm(yn1);
if en<TOL
%Se acepta el paso
tn=tn+hn;yn=yn1;
%Si se ha llegado al final del intervalo
%Se deja de iterar
if tn>=tf
disp('FIN')
break
end
%Se acepta la aproximación
t=[t tn];
y=[y yn];
%Se establece el nuevo paso
rn=0.9*(TOL/en)^p1;
if rn<1|rn>1.1
hn=min(rn,5)*hn;
end
else
disp('Fallo del paso ')
fallo=1;
[en TOL]
end
end
En este ejemplo, al ejecutar el código anterior, se ha aceptado siempre el paso y no es necesario hacer reducción de $h$ en ningún momento.
Teniendo en cuenta el ejemplo 6.17, este PVI modeliza el movimiento de dos cuerpos que se mueven atraidos según la ley de la gravitación universal de Newton. Las coordenadas $(y_1(t),y_2(t))=(y(t),z(t))$ son las de uno de los cuerpos (satélite) con origen el otro cuerpo central. Para representar la solución, que en este caso es una elipse, se debe considerar la primera y segunda componente del vector $y$.
%Representación de la solución aproximada del movimiento
plot(y(1,:),y(2,:),'*')
axis equal
legend('(y(t),z(t))')
El siguiente ejemplo ilustra el procedimiento a seguir cuando resulta necesario reducir el tamaño de paso en algún momento.
Se define en primer lugar el PVI.
f=@(t,y) [1+y(1).^2*y(2)-4*y(1);3*y(1)-y(1)^2.*y(2)];
t0=0;tf=20;y0=[3/2;3];
Se consideran los errores absolutos y relativos y el esquema RKF 4-5.
%Error absoluto y relativo
ea=10^-12;er=10^-10;
%Métodos encajados
[a b c est]=rkf45a;
Se considera el paso inicial.
hmin=(tf-t0)/10^6;p1=0.2; % p1=1/(1+4) p=4 en RKF 4-5
hn=max(hmin,(ea+er*norm(y0))^p1);
Se itera con el mismo código que en el ejemplo anterior, hasta que se produzca un fallo en el paso o se llegue al final del intervalo de integración.
tn=t0;yn=y0;t=[t0];y=[y0];
fallo=0;
while (tn<=tf)&(fallo==0)
%Cálculo del paso con estimación error
[yn1,en]=rkf(f,tn,hn,yn,a,b,c,est);
%Cálculo de la tolerancia
TOL=ea+er*norm(yn1);
if en<TOL
%Se acepta el paso
tn=tn+hn;yn=yn1;
%Si se ha llegado al final del intervalo
%Se deja de iterar
if tn>=tf
disp('FIN')
break
end
%Se acepta la aproximación
t=[t tn]; y=[y yn];
%Se establece el nuevo paso
rn=0.9*(TOL/en)^p1;
if rn<1|rn>1.1
hn=min(rn,5)*hn;
end
else
disp('Fallo del paso ')
fallo=1;
[en TOL]
end
end
Tras varias iteraciones, se produce fallo en el paso, por lo que hay que reducirlo.
%Se reduce el paso
rn=0.9*(TOL/en)^0.2;
hn=min(rn,0.5)*hn;
%Se calcula con el nuevo paso la aproximación
%y le estimación del error
[yn1,en]=rkf(f,tn,hn,yn,a,b,c,est);
TOL=ea+er*norm(yn1);
[en TOL]
Se comprueba que en es menor que TOL por lo que se acepta la aproximación y por prevención se reducen también los siguientes dos pasos.
%Se acepta la aproximación
tn=tn+hn;yn=yn1;t=[t tn];y=[y yn];
%==== Reducción 1
%Se reduce el paso para la siguiente aproximación
rn=0.9*(TOL/en)^0.2;hn=min(rn,1)*hn;
[yn1,en]=rkf(f,tn,hn,yn,a,b,c,est);
TOL=ea+er*norm(yn1);
[en TOL] %Se comprueba que en>TOL
%Dado que en<TOL se acepta la aproximación
tn=tn+hn;yn=yn1;t=[t tn];y=[y yn];
%==== Reducción 2
%Se reduce el paso para la siguiente aproximación
rn=0.9*(TOL/en)^0.2;hn=min(rn,1)*hn;
[yn1,en]=rkf(f,tn,hn,yn,a,b,c,est);
TOL=ea+er*norm(yn1);
[en TOL] %Se comprueba que en<TOL
Como el error es menor que la tolerancia, se acepta el paso y se vuelve a iterar hasta terminar o hasta que se produzca otro fallo.
%Se acepta yn1 y tn calculados anteriormente
tn=tn+hn;yn=yn1;t=[t tn];y=[y yn];
%Se itera hasta que se termine o se produzca fallo
rn=0.9*(TOL/en)^0.2;hn=min(rn,5)*hn;
fallo=0;
while (tn<=tf)&(fallo==0)
%Cálculo del paso con estimación error
[yn1,en]=rkf(f,tn,hn,yn,a,b,c,est);
%Cálculo de la tolerancia
TOL=ea+er*norm(yn1);
if en<TOL
tn=tn+hn;yn=yn1;
%Se acepta la aproximación
t=[t tn]; y=[y yn];
%Se deja de iterar, si es final del intervalo
if tn>=tf
disp('FIN')
break
end
%Se establece el nuevo paso
rn=0.9*(TOL/en)^p1;
if rn<1|rn>1.1
hn=min(rn,5)*hn;
end
else
disp('Fallo del paso ')
fallo=1; [en TOL]
end
end
Vuelve a producirse un fallo, por lo que de nuevo se debe hacer una reducción de $h$ y dos pasos más con reducción por prevención.
rn=0.9*(TOL/en)^0.2; %Se reduce el paso
hn=min(rn,0.5)*hn;
%Calculo nuevo paso y estimación del error
[yn1,en]=rkf(f,tn,hn,yn,a,b,c,est);
TOL=ea+er*norm(yn1);
[en TOL] %Se comprueba que en<TOL
%Se acepta la aproximación
tn=tn+hn;yn=yn1;t=[t tn];y=[y yn];
% ==== Reducción 1
%Se reduce el paso para la siguiente aproximación
rn=0.9*(TOL/en)^0.2;hn=min(rn,1)*hn;
[yn1,en]=rkf(f,tn,hn,yn,a,b,c,est);
TOL=ea+er*norm(yn1);
[en TOL] %Se comprueba que n<TOL
%Dado que en<TOL se acepta la aproximación
tn=tn+hn;yn=yn1;t=[t tn];y=[y yn];
% ==== Reducción 2
%Se reduce el paso para la siguiente aproximación
rn=0.9*(TOL/en)^0.2;hn=min(rn,1)*hn;
[yn1,en]=rkf(f,tn,hn,yn,a,b,c,est);
TOL=ea+er*norm(yn1);
[en TOL] %Se comprueba que en<TOL
tn=tn+hn;yn=yn1;t=[t tn];y=[y yn];
Comprobado que en<TOL, se vuelve a iterar hasta terminar o hasta que haya que hacer una nueva reducciónd e $h$.
%Se establece el nuevo paso
rn=0.9*(TOL/en)^p1;
if rn<1|rn>1.1
hn=min(rn,5)*hn;
end
%Se itera
fallo=0;
while (tn<=tf)&(fallo==0)
%Cálculo del paso con estimación error
[yn1,en]=rkf(f,tn,hn,yn,a,b,c,est);
%Cálculo de la tolerancia
TOL=ea+er*norm(yn1);
if en<TOL
%Se acepta el paso
tn=tn+hn;yn=yn1;
t=[t tn]; y=[y yn];
if tn>=tf
disp('FIN')
break
end
%Se establece el nuevo paso
rn=0.9*(TOL/en)^p1;
if rn<1|rn>1.1
hn=min(rn,5)*hn;
end
else
disp('Fallo del paso ')
fallo=1; [en TOL]
end
end
Como no se vuelve a producir ningún fallo en el paso, se llega al final del intervalo. El número de pasos realizados es 61, basta ver el número de componentes del vector t escribiendo el código Matlab/Octave length(t)-1.
En la siguiente figura se muestra la solución del PVI en el intervalo $[0,1]$.
Considerando $y_1=y$, $y_2=y'$, $y_3=y''$, el PVI se podrá escribir de la forma
$$\left( {\begin{array}{ccccccccccccccc}{y{'_1}}\\{y{'_2}}\\{y{'_3}}\end{array}} \right) = \left( {\begin{array}{ccccccccccccccc}{{y_2}}\\{{y_3}}\\{1 - {e^t}{y_3} + 10t{y_2} - {y_1}}\end{array}} \right)\,\,\,\,\,\,\,\,\,\left( {\begin{array}{ccccccccccccccc}{{y_1}\left( 0 \right)}\\{{y_2}\left( 0 \right)}\\{{y_3}\left( 0 \right)}\end{array}} \right) = \left( {\begin{array}{ccccccccccccccc}1\\{ - 2}\\0\end{array}} \right)$$En Matlab/Octave se definirá la función de la EDO y las condiciones iniciales de la forma siguiente.
f=@(t,y) [y(2);y(3);1-exp(t)*y(3)+10*t*y(2)-y(1)];
t0=0;tf=8.9;y0=[1;-2;0];
Se consideran los errores absolutos y relativos y el esquema RKF 4-5.
%Error absoluto y relativo
ea=10^-12;er=10^-10;
%Métodos encajados
[a b c est]=rkf45a;
Se considera el paso inicial.
hmin=(tf-t0)/10^6;p1=0.2; % p1=1/(1+4) p=4 en RKF 4-5
hn=max(hmin,(ea+er*norm(y0))^p1);
Se itera con el mismo código visto en ejemplos anteriores, hasta que se produzca un fallo en el paso o se llegue al final del intervalo de integración.
tn=t0;yn=y0;t=[t0];y=[y0];
fallo=0;
while (tn<=tf)&(fallo==0)
%Cálculo del paso con estimación error
[yn1,en]=rkf(f,tn,hn,yn,a,b,c,est);
%Cálculo de la tolerancia
TOL=ea+er*norm(yn1);
if en<TOL
%Se acepta el paso
tn=tn+hn;yn=yn1;
%Si se ha llegado al final del intervalo
%Se deja de iterar
if tn>=tf
disp('FIN')
break
end
%Se acepta la aproximación
t=[t tn]; y=[y yn];
%Se establece el nuevo paso
rn=0.9*(TOL/en)^p1;
if rn<1|rn>1.1
hn=min(rn,5)*hn;
end
else
disp('Fallo del paso ')
fallo=1; [en TOL]
end
end
Tras varias iteraciones, se produce fallo en el paso, por lo que hay que reducirlo.
%Se reduce el paso
rn=0.9*(TOL/en)^0.2;
hn=min(rn,0.5)*hn;
%Se calcula con el nuevo paso la aproximación
%y le estimación del error
[yn1,en]=rkf(f,tn,hn,yn,a,b,c,est);
TOL=ea+er*norm(yn1); [en TOL]
Se comprueba que en es menor que TOL por lo que se acepta la aproximación y por prevención se reducen también los siguientes dos pasos.
%Se acepta la aproximación
tn=tn+hn;yn=yn1;t=[t tn];y=[y yn];
% ==== Reducción 1
%Se reduce el paso para la siguiente aproximación
rn=0.9*(TOL/en)^0.2;hn=min(rn,1)*hn;
[yn1,en]=rkf(f,tn,hn,yn,a,b,c,est);
TOL=ea+er*norm(yn1);
[en TOL] %Se comprueba que en>TOL
%Dado que en<TOL se acepta la aproximación
tn=tn+hn;yn=yn1;t=[t tn];y=[y yn];
% ==== Reducción 2
%Se reduce el paso para la siguiente aproximación
rn=0.9*(TOL/en)^0.2;hn=min(rn,1)*hn;
[yn1,en]=rkf(f,tn,hn,yn,a,b,c,est);
TOL=ea+er*norm(yn1);
[en TOL] %Se comprueba que en<TOL
Como el error es menor que la tolerancia, se acepta el paso y se vuelve a iterar no produciéndose ningún fallo y llegando al final del intervalo. En la gráfica siguiente se muestra la solución del problema.
En este apartado se estudiará el problema de contorno siguiente:
$$\begin{aligned} & y''\left( t \right) = f\left( {t,y\left( t \right),y'\left( t \right)} \right)\,\,\,\,\,\,\,\,t \in \left[ {{t_o},{t_f}} \right] \cr & y\left( {{t_o}} \right) = {y_o}\,\,\,\,\,,\,\,\,\,y\left( {{t_f}} \right) = {y_f} \end{aligned}$$Al carecer de la condición $y'(t_0)$, no es posible integrar directamente con Runge-Kutta. En su lugar, se formula y resuelve el siguiente problema de valor inicial:
$$(P) \,\,\,\,\left\{ \begin{aligned} & y{'_1}\left( t \right) = {y_2}\left( t \right) \\ & y{'_2}\left( t \right) = f\left( {t,{y_1}\left( t \right),{y_2}\left( t \right)} \right)\,\,\,\,\,\,\,t \in \left[ {{t_o},{t_f}} \right] \\ & y_1\left( {{t_o}} \right) = {y_o}\,\,\,\,\,,\,\,\,\,y_2\left( {{t_o}} \right) = x \end{aligned} \right.$$buscando el valor de
$x$ de forma que la solución $y_x=(y_{x,1},y_{x_2})^T$ cumpla que $y_{x,1}$ para el valor de $t=t_f$
sea $y_f$
Para resolver este problema con Matlab/Octave se puede utilizar la función oderkf.m desarrollada por Eduardo Casas (ficheros Matlab que resuelve el problema de valor inicial (P) para un valor de $x$ dado. Esta función tiene la siguiente sintáxis:
[t,y]=oderkf(f,t0,y0,tf,ea,er)
Una vez resuelto el problema de valor inicial P con pendiente inicial $x$, el siguiente paso es encontrar el valor de $x$ que haga que la solución satisfaca la condición en el extremo, es decir, $y_1(t_f)=y_f$. Para ello se define la función $g(x)$ buscando el cero de $g(x)=y_1(t_f)-y_f$ por el método de la secante.
function [gx,tx,yx]=g(x)
f=...; $función que define la EDO
to=...;tf=...; %Intervalo
y0=...; % Valor inicial de y1 en to
yo=[y0;x];
ea=...; er=...; %Error absoluto y relativo
%Resolución del problema de valor inicial P
[tx,yx]=oderkf(f,to,yo,tf,ea,er);
%La condición es y1(tf)=yf;
gx=yx(1,end)-yf;
end
Se ilustra este procedimiento en el siguiente ejemplo.
Paso 1. Se considera el problema de valor inicial a resolver en $[to,tf]=[1,2]$ considerando $y_1=y$, $y_2=y'$
$$\left( {\begin{array}{ccccccccccccccc}{y{'_1}}\\{y{'_2}}\end{array}} \right) = \left( {\begin{array}{ccccccccccccccc}{{y_2}}\\{\frac{{{{\left( {{y_1} - t{y_2}} \right)}^3}}}{{{t^3}}}}\end{array}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {\begin{array}{ccccccccccccccc}{{y_1}\left( 0 \right)}\\{{y_2}\left( 0 \right)}\end{array}} \right) = \left( {\begin{array}{ccccccccccccccc}0\\x\end{array}} \right)$$La solución vectorial del problema $y_x(t)$ tiene como primera componente la función solución y la segunda su derivada
$$y_x(t)=(y(t),y'(t))$$Paso 2. Se define la función $g(x)=y_{x1}(t_f)-y_f$ siendo $t_f=2$ e $y_f=y(2)=2$. A continuación se aplica el método de la secante para encontrar el valor de $x$ que hace $g(x)=0$.
function [gx,tx,yx]=g(x)
f=@(t,y) [y(2);1/t^3*(y(1)-t*y(2))^2];
to=1;
tf=2;
yo=[0;x];
ea=10^-14;
er=10^-12;
%Se resuelve el problema de valor inicial
[tx yx]=oderkf(f,to,yo,tf,ea,er);
gx=yx(1,end)-2; %Valor final igual a tf
end
Paso 3. Se aplica el método de la secante a la función $g(x)$ para hallar $x$ de forma que $g(x)=0$.
format long
%se busca cambio de signo
[g(1) g(1.5)]
%Se aplica el método de la secante
x0=1;x1=1.5;tol=10^-12;
gx0 = g(x0);
gx1 = g(x1);
em =eps/2;
maxiter=1000;
for i = 1:maxiter
mk = (gx1-gx0)/(x1-x0);
if abs(mk)>em*abs(gx1)
xk = x1 - gx1/mk;
else
disp('Error secante')
break
end
if abs(xk - x1) < tol
disp('Solución raíz')
[x1 g(x1)]
break;
end
x0=x1;gx0=gx1;
x1=xk;gx1=g(xk);
end
%Solución: 1.264241117657183
Paso 4. Encontrado $x$, la solución del problema se obtiene con la función $g$ que devuelve en el segundo parámetro de salida el vector $t$ y en el tercero el vector $y$.
x=1.264241117657183;
%tx es el vector t, yx es la solución del problema
[gx,tx,yx]=g(x);
Se dibuja la solución del problema de contorno.
%Se dibuja la solución
plot(tx,yx(1,:),'o')
Se compara con la solución general, que en este caso es conocida. La solución es $y\left( t \right) = t\log \left( {\frac{t}{{{C_1}t + 1}}} \right) + {C_2}t\,\,$ con ${C_1} = \frac{{2 - e}}{{2e - 2}}\,$ y $\,{C_2} = \log \left( {{C_1} + 1} \right)$.
%Solución real:
tsol=1:0.05:2;
C1=(2-exp(1))/(2*exp(1)-2);C2=log(C1+1);
ysol=tsol.*log(tsol./(C1*tsol+1))+C2*tsol;
hold on
plot(tsol,ysol)
hold off
legend('Sol Met. Tiro', 'Solución exacta')
Paso 1. Se considera el problema de valor inicial a resolver en $[to,tf]=[1,2]$ considerando $y_1=y$, $y_2=y'$
$$\left( {\begin{array}{ccccccccccccccc}{y{'_1}}\\{y{'_2}}\end{array}} \right) = \left( {\begin{array}{ccccccccccccccc}{{y_2}}\\ {t{y^3}\left( t \right) - 1 - sen\left( t \right)}\end{array}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {\begin{array}{ccccccccccccccc}{{y_1}\left( 0 \right)}\\{{y_2}\left( 0 \right)}\end{array}} \right) = \left( {\begin{array}{ccccccccccccccc}0\\x\end{array}} \right)$$La solución vectorial del problema $y_x(t)$ tiene como primera componente la función solución y la segunda su derivada
$$y_x(t)=(y(t),y'(t))$$Paso 2. Se define la función $g(x)=y_{x1}(t_f)-y_f$ siendo $t_f=\pi/2$ e $y_f=y(\pi/2)=1$. A continuación se aplica el método de la secante para encontrar el valor de $x$ que hace $g(x)=0$.
function [gx,tx,yx]=ga(x)
f=@(t,y) [y(2);t*y(1)^3-1-sin(t)];
to=0;
tf=pi/2;
yo=[0;x];
ea=10^-14;
er=10^-12;
%Se resuelve el problema de valor inicial
[tx yx]=oderkf(f,to,yo,tf,ea,er);
gx=yx(1,end)-1; %Valor final igual a tf
end
Paso 3. Se aplica el método de la secante a la función $ga(x)$ para hallar $x$ de forma que $ga(x)=0$.
%se busca cambio de signo
[ga(1) ga(2)]
%Se aplica el método de la secante
x0=1;x1=2;tol=10^-12;
gx0 = ga(x0);
gx1 = ga(x1);
em =eps/2;
maxiter=1000;
for i = 1:maxiter
mk = (gx1-gx0)/(x1-x0);
if abs(mk)>em*abs(gx1)
xk = x1 - gx1/mk;
else
disp('Error secante')
break
end
if abs(xk - x1) < tol
disp('Solución raíz')
[x1 ga(x1)]
break;
end
x0=x1;gx0=gx1;
x1=xk;gx1=ga(xk);
end
%Valor x=1.809633743684593
Paso 4. Encontrado $x$, la solución del problema se obtiene con la función $ga$ que devuelve en el segundo parámetro de salida el vector $t$ y en el tercero el vector $y$.
x=1.809633743684593;
%tx es el vector t, yx es la solución del problema
[gx,tx,yx]=ga(x);
Se dibuja la solución del problema de contorno.
%Se dibuja la solución
plot(tx,yx(1,:),'o')
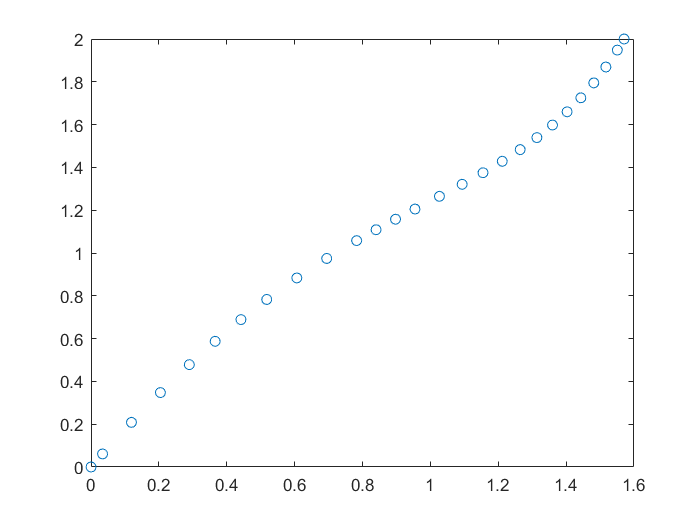
El método puede adaptarse fácilmente al siguiente ejemplo.
pudiendo escribirse el problema de la forma siguiente
$$\begin{aligned} & y'_1 = {y_2}\\ & y'_2 = sen\left( {{y_1}} \right) + 0.01\,\, t\,\, {y_1} + 0.1\,\, {y_3}\\ & y'_3\left( t \right) = sen\left( {{y_1} + {y_3}} \right) + {y_4}\\ & y'_4\left( t \right) = \cos \left( {{y_1} + {y_3} + {y_4}} \right)\\ & {y_1}\left( 0 \right) = 0 = {y_3}\left( 0 \right),\,\,\,\,\,{y_4}\left( 0 \right) = 1\,\,,\,\,\,\,\,\,{y_2}\left( 0 \right) = x \end{aligned}$$El procedimiento buscará $x$ para que la solución del PVI, $yx$, verifique
$${y_{x,1}}\left( \pi \right) + {y_{x,3}}\left( \pi \right)+ {y_{x,4}}\left( \pi \right) = 0$$ La función a la que aplicar el método de la secante será la siguiente.
function [gx,tx,yx]=ge(x)
f=@(t,y) [y(2);sin(y(1))+0.01*t*y(1)+0.1*y(3);
sin(y(1)+y(3))+y(4);cos(y(1)+y(3)+y(4)]
to=0;
tf=pi;
yo=[0;x;0;1];
ea=10^-14;
er=10^-12;
%Se resuelve el problema de valor inicial
[tx yx]=oderkf(f,to,yo,tf,ea,er);
gx=yx(1,end)+yx(3,end)+yx(4,end); %Condición en el extremo
end
ode45 considerando como tolerancia absoluta y relativa respectivamente:\(10^{-8}\) y \(10^{-6}\):
\[ \begin{aligned} y'' &= -\,0.65\,y' \;+\; 0.1\,z \;-\; 0.5\,\cos(t), \\[6pt] z'' &= -\,\sin(t) \;+\; 0.1\,z \;+\; w, \\[6pt] w'' &= \cos(t) \;+\; 0.1\,w, \quad t \in [0,\,10], \end{aligned} \] con condiciones iniciales \[ y(0) = 1,\; y'(0) = 0,\quad z(0) = 0,\; z'(0) = 1,\quad w(0) = 0,\; w'(0) = 0. \]
ode45 usando el método de Runge-Kutta-Fehlberg con tolerancia \( \varepsilon_a =10^{-12} \), \( \varepsilon_r = 10^{-10} \).
En este capítulo se trata la integración numérica de ecuaciones diferenciales, una herramienta fundamental en la resolución de problemas matemáticos y científicos que no tienen solución analítica. Este capítulo presenta diversas técnicas para resolver problemas de valor inicial mediante métodos numéricos y analiza sus características, errores y aplicabilidad.
Los contenidos principales del capítulo son los siguientes.
Se introduce el concepto de ecuaciones diferenciales ordinarias (EDO) y su resolución a través de condiciones iniciales dadas, planteando el problema como una base para aplicar métodos numéricos.
Explicación de las condiciones bajo las cuales las soluciones de las EDO están garantizadas y son únicas, un punto clave para entender la validez de los métodos numéricos.
Este es el método numérico más básico para resolver EDO. Se describe su implementación, ventajas y desventajas, además de discutir el error global acumulado.
Una mejora del método de Euler que utiliza una corrección iterativa para aumentar la precisión. También conocido como método del trapecio, es un ejemplo de método de orden 2.
Se analizan los métodos de mayor precisión basados en evaluaciones de la pendiente intermedia, destacando el método de cuarto orden como estándar debido a su equilibrio entre precisión y esfuerzo computacional.
Se detalla cómo se evalúan y minimizan los errores locales y globales en los métodos Runge-Kutta, incluyendo estrategias para ajustar el tamaño del paso.
Introducción a los métodos adaptativos que ajustan dinámicamente el tamaño del paso en función de una estimación del error, optimizando la eficiencia y precisión del cálculo.
Este apartado aborda problemas de contorno, en los cuales las condiciones iniciales y finales están especificadas. Se introduce el método de tiro como técnica para aproximar soluciones.