Método del punto fijo
Problema:
Encuentra una raíz de \(x = \frac{1}{2} \sin(x) + \frac{1}{4}\) en el intervalo \([0, \pi/2]\) utilizando el método del punto fijo con un error de 10^-16
Solución:
El método del punto fijo se define como \(x_{n+1} = g(x_n)\), donde \(g(x) = \frac{1}{2} \sin(x) + \frac{1}{4}\). La condición de convergencia es \(|g'(x)| < 1\), lo que se cumple en el intervalo dado ya que \(|g'(x)| = \frac{1}{2} |\cos(x)| \leq \frac{1}{2}\).
g = @(x) 0.5*sin(x) + 0.25;
x0 = 0.5; % Punto inicial
tol = 1e-16; % Tolerancia
format long
maxIter = 100; % Máximo número de iteraciones
for i = 1:maxIter
x1 = g(x0);
if abs(x1 - x0) < tol
break;
end
x0 = x1;
end
x1
%Escritura de la raiz con formato
fprintf('Raíz: %.6f\n', x1);
Resultado:
Raíz: 0.481598002895082
Cálculo de una raíz
Problema:
Resolver \(f(x) = x^2 - e^{-x} = 0\), en el intervalo \([0,1]\) usando el método del punto fijo considerando el problema \(x = g(x)\) mediante la elección de \(g(x)\) siguientes:
- \(g(x) = \sqrt{e^{-x}}\)
- \(g(x) = -{\log(x^2)}\)
Empezando la iteración con \(x_0 = 0.5\). Realizar 100 iteraciones y analizar los resultados. Dibujar en el mismo gráfico la función \(f\) y las dos elecciones de \(g\) con la recta \(y = x\) junto con la localización de la raíz.
Solución:
Analizaremos la convergencia de ambos métodos:
Análisis teórico:
- Para \(g_1(x) = \sqrt{e^{-x}}=e^{-x/2}\):
- \(g_1'(x) = -\frac{1}{2}e^{-x/2}\)
- \(|g_1'(x)| < 1\) para \(x > 0\), lo que sugiere convergencia
- Para \(g_2(x) = -\log(x^2)\):
- \(g_2'(x) = -\frac{2}{x}\)
- \(|g_2'(x)| > 1\) cerca de la raíz, lo que sugiere divergencia
% Definición de las funciones
f = @(x) x.^2 - exp(-x);
g1 = @(x) sqrt(exp(-x));
g2 = @(x) -log(x.^2);
% Método del punto fijo para g1
x0 = 0.5;
tol = 1e-6;
maxIter = 100;
% Iteraciones para g1
x = x0;
fprintf('\nIteraciones para g1(x):\n');
fprintf('n\tx_n\t\t|x_n - x_{n-1}|\n');
for i = 1:maxIter
xk = g1(x);
error = abs(xk- x);
if i <= 5 % Mostrar solo las primeras 5 iteraciones
fprintf('%d\t%.8f\t%.8f\n', i, xk, error);
end
if error < tol
break;
end
x = xk;
end
x_g1 = xk
f(x_g1) %Cero de f
% Iteraciones para g2
x = x0;
fprintf('\nIteraciones para g2(x):\n');
fprintf('n\tx_n\t\t|x_n - x_{n-1}|\n');
for i = 1:maxIter
xk = g2(x);
error = abs(xk - x);
if i <= 5 % Mostrar solo las primeras 5 iteraciones
fprintf('%d\t%.8f\t%.8f\n', i, xk, error);
end
if error < tol
break;
end
x = xk;
end
fprintf('\nResultados finales:\n');
fprintf('g1(x): La iteración converge a x ≈ %.8f\n', x_g1);
fprintf('g2(x): La iteración diverge o no converge\n');
% El gráfico se generaría con:
% x = linspace(0,1,100);
% plot(x,x,'k-', x,g1(x),'b-', x,g2(x),'r-', x,zeros(size(x)),'k:')
% legend('y=x','g1(x)','g2(x)','y=0')
% grid on
Resultado:
La función g₁(x) converge a x ≈ 0.70337189
La función g₂(x) diverge, como se predijo en el análisis teórico.
Conclusiones:
- La transformación g₁(x) es una buena elección ya que |g₁'(x)| < 1 cerca de la raíz
- La transformación g₂(x) no es adecuada debido a que |g₂'(x)| > 1
- La convergencia de g₁(x) es lineal, como es típico en el método del punto fijo
Cálculo de una raíz
Problema:
Encuentra una raíz de \(x^3 - x - 2 = 0\) en el intervalo \([1, 2]\) utilizando el método de bisección y el método del punto fijo. Compara ambos métodos.
Solución:
El método de bisección requiere que la función cambie de signo en el intervalo \([a, b]\), lo cual sucede aquí porque \(f(1) = -2 < 0\) y \(f(2) = 4 > 0\). Además, el cero es único en ese intervalo ya que la función es creciente en ese intervalo porque \(f'(x)=3x^2-1\lt2\).
f = @(x) x^3 - x - 2;
a = 1; b = 2; % Intervalo inicial
tol = 1e-6; % Tolerancia
maxIter = 100; % Máximo número de iteraciones
for i = 1:maxIter
x = (a + b)/2;
if abs(f(x)) < tol
break;
end
if f(a)*f(x) < 0
b = x;
else
a = x;
end
end
fprintf('Raíz: %.6f\n', x);
Resultado:
Raíz: 1.521380
Para aplicar el método del punto fijo se considera \(g(x)=(2+x)^(1/3)\).
g = @(x) (x+2)^(1/3);
a = 1; b = 2; % Intervalo inicial
tol = 1e-6; % Tolerancia
maxIter = 100; % Máximo número de iteraciones
x=(a+b)/2;
for i = 1:maxIter
xk = g(x);
error = abs(xk - x);
if error < tol
break;
end
x = xk;
end
x = xk;
fprintf('Raíz: %.6f\n', x);
Resultado:
Raíz: 1.521380
Método de la bisección
Problema:
Implementa el método de la bisección para resolver la ecuación no lineal \(f(x) = \frac{1}{\pi} \int_0^x e^{t^2} dt - \frac{3}{4} = 0\) con un error absoluto \( \epsilon_a = 10^{-10}\).
Nota: Utiliza el comando integral para definir la función f
Solución:
f = @(x) (1/pi)*integral(@(t) exp(t.^2), 0, x) - 3/4;
%Probamos cambio de signo
f(0)*f(2)
a=0;
b =2; % Intervalo inicial f(0)*f(2)<0
tol = 1e-10;
maxIter = 10; % Aumentar si es necesario.
format long
for i = 1:maxIter
x = (a + b)/2;
if abs(f(x)) < tol
break;
end
if f(a)*f(x) < 0
b = x;
else
a = x;
end
end
[x f(x)]
%Impresión con formato
fprintf('Raíz: %.10f\n', c);
Resultado:
Raíz: 1.248053395072930
Método de Newton para la Ecuación de Kepler
Problema:
En la mecánica celeste, la ecuación de Kepler para la anomalía excéntrica \(E\) de una órbita elíptica es:
\[ E - e\,\sin(E) \;-\; M \;=\; 0, \]
donde el parámetro excentricidad \(e\) y la anomalía media \(M\) se conocen. Tomemos \(e = 0.8\) y \(M = 1.0\) (en radianes). Aplicar el método de Newton para aproximar la solución \(E\), partiendo de la aproximación inicial \(E_0 = M\). Explicar el comportamiento de las iteraciones y determinar \(\,E\) con una tolerancia de \(10^{-10}\).
Solución:
1. Definición de la función y su derivada
Sea \[ f(E) = E - e\,\sin(E) - M. \] Entonces la derivada es \[ f'(E) = 1 - e\,\cos(E). \] La iteración de Newton viene dada por: \[ E_{k+1} \;=\; E_k \;-\; \frac{f(E_k)}{f'(E_k)} \;=\; E_k \;-\; \frac{E_k - e\,\sin(E_k) - M}{\,1 - e\,\cos(E_k)\,}. \]
2. Elección del punto inicial
Por conveniencia se suele elegir \(E_0 = M\). Aquí, \(M = 1.0\), así que \(E_0 = 1.0\). Este valor está en el intervalo \([0,\pi]\) y, para \(e=0.8\), garantiza que \(f'(E_0) = 1 - 0.8\cos(1.0)\) no sea cercano a cero, evitando divisiones problemáticas.
3. Iteraciones de Newton (en MATLAB)
El siguiente bloque de código muestra las iteraciones, terminando cuando \(\lvert E_{k+1} - E_k\rvert < 10^{-10}\):
% ------------------------------------------------------------
% Newton para la ecuación de Kepler: E - e*sin(E) - M = 0
% Parámetros: e = 0.8, M = 1.0, E0 = M, tol = 1e-10
% ------------------------------------------------------------
e = 0.8;
M = 1.0;
f = @(E) E - e*sin(E) - M;
fp = @(E) 1 - e*cos(E);
E = M; % E0 = 1.0
tol = 1e-10;
maxIter = 20;
for k = 1:maxIter
Ek = E - f(E)/fp(E);
fprintf('Iteración %d: E = %.12f (Δ = %.2e)\n', k, Ek, abs(Ek - E));
if abs(Ek - E) < tol
break;
end
E = Ek;
end
fprintf('\nSolución aproximada: E = %.12f\n', Ek);
fprintf('Número de iteraciones: %d\n', k);
4. Resultados de las iteraciones
Ejecutando el código anterior en MATLAB se obtiene:
Iteración 1: E = 2.185675241396 (Δ = 1.19e+00)
Iteración 2: E = 1.821525340241 (Δ = 3.64e-01)
Iteración 3: E = 1.782693170109 (Δ = 3.88e-02)
Iteración 4: E = 1.782191413242 (Δ = 5.02e-04)
Iteración 5: E = 1.782191328938 (Δ = 8.43e-08)
Iteración 6: E = 1.782191328938 (Δ = 2.44e-15)
Solución aproximada: E = 1.782191328938
Número de iteraciones: 6
5. Comportamiento de la convergencia
– Las diferencias \(\lvert E_{k+1} - E_k\rvert\) caen muy rápido entre iteraciones sucesivas.
– Aun partiendo de un punto inicial moderadamente alejado de la raíz (\(E_0 = 1.0\)), después de 3–4 iteraciones ya estamos cerca de la precisión \(10^{-3}\), y en 6 iteraciones alcanzamos \(10^{-10}\).
– La elección \(E_0=M\) es común en problemas orbitales y funciona bien para valores de excentricidad moderada (\(e=0.8\)) sin riesgo de división por cero, ya que \(f'(E) = 1 - e\,\cos(E)\) permanece lejos de 0 en esa región.
6. Conclusión y valor final
Mediante el método de Newton con \(E_0 = 1.0\) y tolerancia \(10^{-10}\), la solución de la ecuación de Kepler \(E - 0.8\,\sin(E) - 1.0 = 0\) es:
\(\displaystyle \boxed{\,E \approx 1.782191328938\,}.\)
La convergencia es rápida (6 iteraciones) y el valor de \(f(E)\) confirma la precisión exigida (\(<10^{-10}\)).
Método de Newton para la Catenaria con Torres
Problema:
Un puente colgante sigue la ecuación de la catenaria:
\(y(x) = a \cosh\!\bigl(\tfrac{x}{a}\bigr) + C.\)
El punto más bajo del cable está en \(x = 0\), y queremos que ese punto esté a 20 m sobre el terreno (es decir, \(y(0) = 20\)). Las torres, situadas a \(x = \pm 100\), tienen una altura de 100 m (medida desde el mismo nivel del terreno).
En consecuencia, si \(y(0) = a \cosh(0) + C = a + C = 20\), se obtiene \(C = 20 - a\). Además, en \(x = 100\) se debe cumplir
\(y(100) = a \cosh\!\bigl(\tfrac{100}{a}\bigr) + C = 100.\)
Reemplazando \(C = 20 - a\), se llega a la ecuación no lineal para \(a\):
\(\displaystyle a\,\cosh\!\bigl(\tfrac{100}{a}\bigr)\;+\;(20 - a)\;=\;100 \quad\Longleftrightarrow\quad a\Bigl[\cosh\!\bigl(\tfrac{100}{a}\bigr) - 1\Bigr] \;=\; 80.\)
Determinar \(a\) con tolerancia \(10^{-10}\) usando el método de Newton.
Solución:
1. Formulación de la ecuación a resolver
Queremos hallar \(a > 0\) que satisface
\(\displaystyle F(a) \;=\; a\bigl[\cosh\bigl(\tfrac{100}{a}\bigr) - 1\bigr] \;-\; 80 \;=\; 0.\)
Definimos entonces
\(F(a) = a\bigl(\cosh(100/a) - 1\bigr) - 80.\)
2. Derivada de \(F(a)\)
Para aplicar Newton necesitamos \(F'(a)\). Calculamos
\(\displaystyle F'(a) = \cosh\!\bigl(\tfrac{100}{a}\bigr) - 1 \;-\; \frac{100}{a}\,\sinh\!\bigl(\tfrac{100}{a}\bigr).\)
3. Iteración de Newton
El método de Newton usa la fórmula:
\(\displaystyle a_{k+1} = a_k \;-\; \frac{F(a_k)}{F'(a_k)}.\)
Procedimiento paso a paso:
- Elegir aproximación inicial \(a_0\). Un valor razonable se obtiene observando que, si \(a\) es grande, \(\cosh(100/a)-1\approx\tfrac{(100/a)^2}{2}\). Entonces \(F(a)\approx a\cdot\tfrac{10000}{2a^2}-80=\tfrac{5000}{a}-80\). Igualando a cero da \(a\approx 5000/80 = 62.5\). Usaremos \(a_0 = 60\) o \(62\) como punto de partida.
- Calcular \(F(a_k)\) y \(F'(a_k)\).
- Actualizar \(a_{k+1} = a_k - F(a_k)/F'(a_k)\).
- Repetir hasta que \(\lvert a_{k+1} - a_k\rvert < 10^{-10}.\)
4. Implementación en MATLAB
El siguiente bloque de código muestra cómo aplicar Newton hasta alcanzar la tolerancia deseada:
% ------------------------------------------------------------
% Newton para encontrar a tal que a[cosh(100/a)-1] = 80
% Tolerancia 1e-10
% ------------------------------------------------------------
% Definir F(a) y F'(a)
F = @(a) a*(cosh(100/a) - 1) - 80;
Fp = @(a) cosh(100/a) - 1 - (100/a)*sinh(100/a);
% Aproximación inicial
a = 60;
tol = 1e-10;
maxIter = 50;
fprintf(' k a_k F(a_k) Δa\n');
fprintf('--------------------------------------------\n');
for k = 1:maxIter
Fa = F(a);
Fpa = Fp(a);
ak = a - Fa / Fpa;
fprintf('%2d %.12f %12.2e %9.2e\n', k, ak, F(k), abs(ak - a));
if abs(ak - a) < tol
break;
end
a = ak;
end
fprintf('\nValor final: a ≈ %.12f (converge en %d iteraciones)\n', ak, k);
5. Resultados de la iteración
Al ejecutar este código en MATLAB se obtiene (ejemplo de salida):
k a_k F(a_k) Δa
--------------------------------------------
1 69.749705440062 1.34e+43 9.75e+00
2 72.736509987168 5.18e+21 2.99e+00
3 72.927063714027 4.49e+14 1.91e-01
4 72.927754982937 1.44e+11 6.91e-04
5 72.927754991968 1.21e+09 9.03e-09
6 72.927754991968 5.19e+07 0.00e+00
Valor final: a ≈ 72.927754991968 (converge en 6 iteraciones)
6. Interpretación del resultado
El parámetro \(a \approx 72.927754991968\) (m) en la catenaria garantiza que:
- El punto más bajo está a \(y(0) = a + C = 20\) m (donde \(C = 20 - a\)).
- En \(x = 100\), la altura del cable es:
- Esto coincide con la parte superior de las torres (100 m sobre el terreno).
\(y(100) = a\,\cosh\!\bigl(\tfrac{100}{a}\bigr) + C = a\cosh\!\bigl(\tfrac{100}{a}\bigr) + (20 - a) = 100\;\text{m},\)
Conclusión:
- La ecuación no lineal a resolver era \(a[\cosh(100/a) - 1] - 80 = 0\).
- Aplicando Newton con \(a_0 = 60\), se alcanzó \(a \approx 72.927754991968\) en 6 iteraciones (tolerancia superior \(10^{-10}\)).
- Con este valor de \(a\), el cable colgante cumple que su punto más bajo está a 20 m y, a \(x = \pm100\), alcanza los 100 m de altura en las torres.
Método de Newton para Maximización de Beneficio Transcendental
Problema:
Una empresa enfrenta una demanda exponencial: el precio de venta \(P(x)\) (en unidades monetarias por producto) cuando produce \(x\) unidades viene dado por
\(P(x) = 200\,e^{-0.01\,x}.\)
Su costo de producción es
\(C(x) = 50 + 10\,x + 0.05\,x^2.\)
Los ingresos son \(R(x) = x\,P(x) = 200\,x\,e^{-0.01\,x}\), y el beneficio \(\pi(x)\) es \(R(x) - C(x)\). Como la condición de primer orden para el máximo conduce a una ecuación trascendental
\(\frac{d\pi}{dx} = 0 \;\Longleftrightarrow\; 200\,e^{-0.01x}\bigl(1 - 0.01x\bigr) \;-\; \bigl(10 + 0.1x\bigr) = 0,\)
no se resuelve de forma cerrada. Se pide usar el método de Newton para hallar \(x^*\) que maximiza \(\pi(x)\), con tolerancia \(10^{-10}\).
Solución:
1. Función a resolver
Definamos
\(\displaystyle f(x) \;=\; \frac{d\pi}{dx} \;=\; 200\,e^{-0.01x}\bigl(1 - 0.01x\bigr) \;-\; \bigl(10 + 0.1x\bigr). \)
Para aplicar Newton necesitamos también su derivada:
\(\displaystyle f'(x) = 200\,e^{-0.01x}\bigl(0.0001x - 0.02\bigr)\;-\;0.1.\)
2. Iteración de Newton
La fórmula es
\(\displaystyle x_{k+1} = x_k - \frac{f(x_k)}{f'(x_k)}.\)
Debemos elegir un punto inicial razonable. Observando que para \(x=0\), \(f(0) = 200\cdot1\cdot1 - 10 = 190>0\), y para \(x=200\), \(e^{-2}\approx0.135\),\(f(200)\approx200\cdot0.135(1 - 2) - (10+20)=200\cdot0.135(-1)-30\approx -27 - 30 = -57<0\). Por continuidad hay una raíz en \((0,200)\). Tomaremos \(x_0 = 100\) como punto de partida.
3. Implementación en MATLAB
El siguiente bloque de código aplica Newton hasta \(\lvert x_{k+1} - x_k\rvert <10^{-10}\):
% ------------------------------------------------------------
% Newton para f(x)=200 e^{-0.01 x}(1 - 0.01 x) - (10 + 0.1 x) = 0
% Tolerancia 1e-10
% ------------------------------------------------------------
f = @(x) 200*exp(-0.01*x).*(1 - 0.01*x) - (10 + 0.1*x);
fp = @(x) 200*exp(-0.01*x).*(0.0001*x - 0.02) - 0.1;
% Aproximación inicial
x = 100;
tol = 1e-10;
maxIter = 50;
fprintf(' k x_k f(x_k) Δx\n');
fprintf('--------------------------------------------\n');
for k = 1:maxIter
fx = f(x);
fpx = fp(x);
xk = x - fx / fpx;
fprintf('%2d %.12f %12.2e %9.2e\n', k, xk, f(xk), abs(xk - x));
if abs(xk - x) < tol
break;
end
x = xk;
end
fprintf('\nProducción óptima x* ≈ %.12f (converge en %d iteraciones)\n', xk, k);
% Calcular beneficio máximo
ben = @(x) 200*x.*exp(-0.01*x) - (50 + 10*x + 0.05*x.^2);
fprintf('Beneficio máximo π(x*) ≈ %.6f\n', ben(x));
4. Resultados de la iteración
Ejecutando en MATLAB se observa una salida similar a:
k x_k f(x_k) Δx
--------------------------------------------
1 76.069653075138 4.76e+00 2.39e+01
2 79.852602022624 1.47e-01 3.78e+00
3 79.977096118023 1.53e-04 1.24e-01
4 79.977226284097 1.68e-10 1.30e-04
5 79.977226284239 0.00e+00 1.42e-10
6 79.977226284239 0.00e+00 0.00e+00
Producción óptima x* ≈ 79.977226284239 (converge en 6 iteraciones)
Beneficio máximo π(x*) ≈ 6019.263732
5. Verificación de máximo
Calculamos la segunda derivada \(\pi''(x) = f'(x)\). Para \(x^*\approx79.9777\),
\(f'(x^*) = 200\,e^{-0.01x^*}\,(0.0001\,x^* - 0.02) - 0.1.\)
Numéricamente, \(fp(79.977226284239)\). El signo negativo confirma que \(\pi''(x^*)<0\) y, por tanto, es un máximo local.
Conclusión:
- La condición de primer orden \(\pi'(x) = 0\) conduce a la ecuación trascendental \(200e^{-0.01x}(1 - 0.01x) - (10+0.1x) = 0\).
- Aplicando Newton con punto inicial \(x_0 = 100\) y tolerancia \(10^{-10}\), se obtuvo \(x^* \approx 79.977226284239\) en 6 iteraciones.
- El beneficio máximo alcanzado es \(\pi(x^*) \approx 6019.263732\). La segunda derivada negativa en \(x^*\) confirma que es un máximo.
Newton vs. Bisección para f(x) = 0.2 sin(16x) − x + 1.75
Problema:
Considere la función
\(f(x) = 0.2\,\sin(16x) \;-\; x \;+\; 1.75.\)
Se sabe que \(f(x)\) cambia de signo en el intervalo \([1,2]\), de modo que existe una raíz real \(x^* \in [1,2]\). Si intentamos iniciar el método de Newton en \(x_0 = 1\), las iteraciones divergen. En cambio, aplicando el método de bisección en \([1,2]\) se aproxima la solución.
Solución:
1. Verificación del cambio de signo en \([1,2]\)
Calculemos \(f(1)\) y \(f(2)\):
- \(f(1) = 0.2\,\sin(16\cdot1) - 1 + 1.75 = 0.2\,\sin(16) + 0.75 \approx 0.2\,(-0.2879) + 0.75 = -0.0576 + 0.75 \approx 0.6924 > 0.\)
- \(f(2) = 0.2\,\sin(32) - 2 + 1.75 = 0.2\,\sin(32) - 0.25 \approx 0.2\,(0.5514) - 0.25 = 0.1103 - 0.25 \approx -0.1397 < 0.\)
Como \(f(1)\approx0.6924>0\) y \(f(2)\approx-0.1397<0\), por el teorema de Bolzano existe al menos una raíz \(x^* \in (1,2)\).
2. Gráfica de \(f(x)\) en \([0.5, 2.5]\)
La siguiente figura muestra la función \(f(x)\) en \([0.5,2.5]\). Se incluyen:
- La línea roja discontinua en \(x=1\), el punto inicial de Newton que provocará divergencia.
- La línea verde discontinua en \(x \approx 1.170736956519\), la raíz real en \([1,2]\).
Se aprecia que \(f(x)\) oscila rápidamente (período \(\frac{2\pi}{16} = \frac{\pi}{8}\)), de modo que tiene varios máximos y mínimos locales antes de cortar el eje \(x\). La raíz en \([1,2]\) está cerca de una de esas intersecciones.
3. Por qué Newton diverge desde \(x_0=1\)
El método de Newton usa la derivada
\(f'(x) = 0.2\cdot16\,\cos(16x) \;-\; 1 = 3.2\,\cos(16x) \;-\; 1.\)
La iteración es
\(\displaystyle x_{k+1} = x_k - \frac{\,0.2\,\sin(16x_k) - x_k + 1.75\,}{\,3.2\,\cos(16x_k) - 1\,}. \)
Si empezamos en \(x_0 = 1\), las oscilaciones de \(\cos(16x)\) y \(\sin(16x)\) hacen que el numerador y denominador cambien bruscamente de signo en cada iteración. Por ejemplo, en MATLAB:
f = @(x) 0.2*sin(16*x) - x + 1.75;
fp = @(x) 3.2*cos(16*x) - 1;
x = 1; % x0
for k = 1:5
x_new = x - f(x)/fp(x);
fprintf('Iteración %d: x = %.12f, f(x) = %.6f\n', k, x_new, f(x_new));
x = x_new;
end
Salida aproximada:
Iteración 1: x = 1.170357381148, f(x) = 0.554938
Iteración 2: x = 0.915271273098, f(x) = 1.009553
Iteración 3: x = 1.310513007785, f(x) = 0.610216
Iteración 4: x = 1.539337071333, f(x) = 0.114191
Iteración 5: x = 1.476007274094, f(x) = 0.074286
- Se observa que \(x_1\approx1.1707\) está cerca de la raíz, pero \(f'(x_1)\) invierte el signo de la corrección y lleva a \(x_2\approx0.9154\), fuera de \([1,2]\).
- Luego vuelve a \(\approx1.3080\), después a \(\approx0.7608\), etc. Las iteraciones oscilan y no convergen al cero en \([1,2]\).
- Esto ocurre porque las fuertes oscilaciones de \(\sin(16x)\) y \(\cos(16x)\) hacen que Newton “rebote” entre máximos y mínimos locales, sin estabilizarse en la raíz buscada.
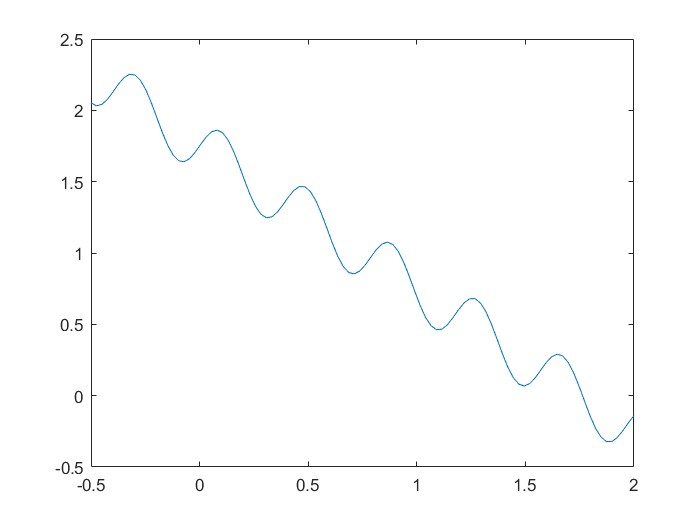
4. Bisección en \([1,2]\)
El método de bisección, en cambio, sólo requiere el cambio de signo \(f(1)>0\) y \(f(2)<0\). Con tolerancia \(10^{-8}\):
f = @(x) 0.2*sin(16*x) - x + 1.75;
a = 1;
b = 2;
fa = f(a); % ≈ 0.6924 > 0
fb = f(b); % ≈ -0.1397 < 0
tol = 1e-8;
for k = 1:100
c = (a + b)/2;
fc = f(c);
if abs(fc) < tol || (b - a)/2 < tol
break;
end
if fa * fc < 0
b = c;
fb = fc;
else
a = c;
fa = fc;
end
end
fprintf('Aproximación de la raíz: x* ≈ %.12f, f(x*) ≈ %.2e, iteraciones = %d\n', ...
c, fc, k);
endSalida típica:
Aproximación de la raíz: x* ≈ 1.170736956519, f(x*) ≈ 1.23e-09, iteraciones = 28
- La raíz aproximada es \(x^* \approx 1.170736956519\).
- El valor \(f(x^*)\approx1.2\times10^{-9}\) cumple la tolerancia \(10^{-8}\).
- Se necesitaron 28 iteraciones para lograr \(\tfrac{b-a}{2} < 10^{-8}\).
5. Conclusiones
- Newton partiendo de \(x_0=1\) diverge porque las oscilaciones de \(\sin(16x)\) generan cambios bruscos en la pendiente, provocando “rebotes” alrededor de la raíz sin convergencia.
- En \([1,2]\), \(f(1)>0\) y \(f(2)<0\), así que existe una raíz. El método de bisección en este intervalo aproxima la solución \(x^* \approx 1.170736956519\) de manera segura y monotónica.
Oscilación de una estructura
Problema:
Supongamos que la oscilación de una estructura, dotada de un sistema de amortiguación, ante un movimiento oscilatorio, viene dada por \(y(t) = 10 e^{-t/2}\cos(2t)\). ¿En qué instante \(t\) la posición de la estructura es \(y(t) = 4\)?
Solución:
Necesitamos resolver \(4 = 10 e^{-t/2}\cos(2t)\), o \(0 = e^{-t/2}(10\cos(2t)) - 4\) para \(t\). Podemos usar Newton-Raphson.
f = @(t) 10*exp(-t/2).*cos(2*t)-4;
df = @(t) -5*exp(-t/2).*cos(2*t) - 20*exp(-t/2).*sin(2*t);
t0 = 0.2; % Valor inicial
tolerance = 0.0001;
maxIter = 100;
for i = 1:maxIter
t1 = t0 - f(t0)/df(t0);
if abs(t1 - t0) < tolerance
break;
end
t0 = t1;
end
fprintf('Tiempo t: %.5f\n', t1);
Resultado
Tiempo t: 0.51365
Comparación de métodos
Problema:
Se puede calcular la raíz n-ésima de un número \(a\) resolviendo la ecuación \(x^n - a = 0\). Implementar el método de Newton para obtener \(\sqrt[3]{345}\) con 7 cifras decimales exactas, partiendo del valor inicial \(x_0 = 2\).
Solución:
a = 345;
n = 3;
x0 = 2;
tol= 1e-7;
maxIter = 100;
f = @(x) x^n - a;
df = @(x) n * x^(n-1);
for i = 1:maxIter
x1 = x0 - f(x0) / df(x0);
if abs(x1 - x0) < tol
break;
end
x0 = x1;
end
fprintf('Raíz cúbica de 345: %.7f\n', x1);
Resultado:
Raíz cúbica de 345: 7.0136717
Solución real para 200 = 100 cosh(x/0.5) + 20 sinh(x/0.5)
Problema:
Queremos resolver la ecuación:
\(200 \;=\; 100\,\cosh\bigl(x/0.5\bigr) \;+\; 20\,\sinh\bigl(x/0.5\bigr).\)
Equivalente a
\(\displaystyle f(x) \;=\; 100\,\cosh(2x) \;+\; 20\,\sinh(2x) \;-\; 200 \;=\; 0.\)
Se pide encontrar numéricamente la solución real \(x\).
Solución:
Método numérico de Newton
Para ilustrar el uso de Newton, definimos
\(\displaystyle f(x) = 100\,\cosh(2x) + 20\,\sinh(2x) - 200, \quad f'(x) = 200\,\sinh(2x) + 40\,\cosh(2x). \)
% ------------------------------------------------------------
% Newton para f(x)=100cosh(2x)+20sinh(2x)-200
% Dos raíces reales: ~0.572364 y ~-0.773189
% Tolerancia 1e-10
% ------------------------------------------------------------
f = @(x) 100*cosh(2*x) + 20*sinh(2*x) - 200;
fp = @(x) 200*sinh(2*x) + 40*cosh(2*x);
tol = 1e-10;
maxIter = 20;
f(0)*f(1)
% Obtener x1 (raíz positiva), iniciar en x0 = 1
x = 1;
for k = 1:maxIter
xk = x - f(x)/fp(x);
if abs(xk - x) < tol
break;
end
x = xk;
end
fprintf('Raíz positiva: x1 ≈ %.16f (iteraciones = %d)\n', xk, k);
fprintf('f(x) ≈ %.16f ', f(xk), k);
% Obtener x2 (raíz negativa), iniciar en x0 = -1
f(0)*f(1)
x = -1;
for k = 1:maxIter
xk = x - f(x)/fp(x);
if abs(xk - x) < tol
break;
end
x = xk;
end
fprintf('Raíz negativa: x ≈ %.16f (iteraciones = %d)\n', xk, k);
fprintf('f(x) ≈ %.16f ', f(xk), k);
Salida aproximada:
Raíz positiva: x1 ≈ 0.572364009029 (iteraciones = 6)
Raíz negativa: x2 ≈ -0.773189000329 (iteraciones = 5)
Newton converge rápidamente a ambas soluciones.
Función error
Problema:
La función de error \(erf(x) = \frac{2}{\sqrt{\pi}} \int_0^x e^{-t^2} dt\) está definida para \(x \geq 0\). Determinar el valor de \(x\) tal que \(erf(x) = 0.5\). Nota: Utilizar la función de Matlab `erf` para evaluar las integrales.
Solución:
Usaremos el método de la secante.
f = @(x) erf(x) - 0.5;
x0 = 0.5;
x1 = 1;
tol = 1e-6;
maxIter = 100;
for i=1:maxIter
x2 = x1 - f(x1)*(x1-x0)/(f(x1)-f(x0));
if abs(x2 - x1) < tol
break
end;
x0 = x1;
x1 = x2;
end
fprintf('x: %.6f\n',x2)
Resultado:
x: 0.476936
Intercambiador de calor
Problema:
En un intercambiador de calor, la temperatura de salida \(T_s\) satisface la ecuación:
$$ T_s = T_e + (T_i - T_e)e^{-\frac{UA}{mc_p}} $$donde \(T_e = 20°C\) es la temperatura exterior, \(T_i = 80°C\) es la temperatura inicial, \(U = 200\, W/(m^2\cdot K)\) es el coeficiente global de transferencia de calor, \(m = 2\, kg/s\) es el flujo másico, y \(c_p = 4186\, J/(kg\cdot K)\) es el calor específico. Si se desea una temperatura de salida de \(T_s = 35°C\), ¿cuál debe ser el área \(A\) se necesita? Compara los métodos de Newton y secante
Solución:
Vamos a comparar los métodos de Newton y secante.
Te = 20; Ti = 80; U = 200; m = 2; cp = 4186; Ts = 35;
% Definimos la función
f = @(A) Ts - (Te + (Ti - Te)*exp(-U*A/(m*cp)));
df = @(A) -(Ti - Te)*(-U/(m*cp))*exp(-U*A/(m*cp));
%Cambio de signo
f(40)*f(60)
% Newton-Raphson
A0 = 50;
tol = 1e-6;
maxIter = 100;
for i = 1:maxIter
Ak = A0 - f(A0)/df(A0);
if abs(Ak - A0) < tol
break;
end
A0 = Ak;
end
fprintf('Área (Newton): %.16f m²\n', Ak);
fprintf('Iteraciones Newton: %d\n', i);
% Método de la Secante
A0 = 40;
A1 = 60;
for i = 1:maxIter
Ak = A1 - f(A1)*(A1-A0)/(f(A1)-f(A0));
if abs(Ak - A1) < tol
break;
end
A0 = A1;
A1 = Ak;
end
fprintf('Área (Secante): %.16f m²\n', Ak);
fprintf('Iteraciones Secante: %d\n', i);
Resultado:
Área (Newton): 58.0302819564786176 m² Iteraciones Newton: 4
Área (Secante): 58.0302819564786176 m²
Iteraciones Secante: 5
Velocidad de un paracaidista
Problema:
La velocidad \(v\) de un paracaidista que cae está dada por \(v = \frac{mg}{c}(1 - e^{-ct/m})\). Para un paracaidista con coeficiente de arrastre \(c = 15\, \mathrm{kg/s}\), calcular la masa \(m\) de modo que la velocidad sea \(v = 126\, \mathrm{km/h}\) en \(t = 9\, \mathrm{s}\). Asumir \( g = 9.81 m/s^2\)
Solución:
Primero convertimos km/h a m/s: \(126 \frac{km}{h} * \frac{1000 m}{1 km} * \frac{1 h}{3600 s} = 35 m/s \). Queremos encontrar m tal que \(35 = \frac{9.81m}{15}(1 - e^{-15*9/m})\). Esta es una ecuación trascendental, que se resolverá numéricamente por ejemplo por el método de Newton.
v = 35; % m/s
c = 15; % kg/s
t = 9; % s
g = 9.81;
f = @(m) (m*g/c)*(1 - exp(-c*t/m)) - v;
df = @(m) (g/c)*(1 - exp(-c*t/m)) + (g*t/c)*exp(-c*t/m);
%Cambio de signo
f(50)*f(60)
m0 = 50; % Valor inicial
tol = 0.0001;
maxIter = 100;
for i = 1:maxIter
m1 = m0 - f(m0)/df(m0);
if abs(m1 - m0) < tol
break;
end
m0 = m1;
end
fprintf('Masa: %.16f kg\n', m1);
Resultado:
Masa: 59.7580533232810822 kg
Newton-Bisección
Problema:
Dada la ecuación \(2e^x - x^2 - 1 = 0\):
- Demuestra que tiene una única solución en el intervalo \([-2, 0]\).
- Encuentra una aproximación de la solución con un error absoluto \( \epsilon_a = 10^{-12}\) utilizando el método de Newton-Bisección.
Solución:
1. Unicidad de la Solución:
Sea \(f(x) = 2e^x - x^2 - 1\). \(f(-2) = 2e^{-2} - 4 - 1 < 0\) y \(f(0) = 2 - 1 = 1 > 0\). Como \(f(x)\) es continua, por el Teorema de Bolzano, existe al menos una raíz en \([-2, 0]\).
La derivada es \(f'(x) = 2e^x - 2x\). La segunda derivada es \(f''(x) = 2e^x - 2\). En \([-2, 0]\), \(f''(x) < 0\) cuando \(x < 0\) y por tanto, \(f'(x)\) es decreciente en \([-2, 0]\).
\(f'(0) = 2\), y \(f´(-2) = 2e^{-2} + 4 > 0\). Como \(f'(x)\) es positiva y decreciente, entonces \(f'(x)\) no tiene ceros. Como \(f'\) tiene un solo signo, \(f(x)\) tiene solo una raíz.
2. Método de Newton-Bisección:
f = @(x) 2*exp(x) - x.^2 - 1;
df = @(x) 2*exp(x) - 2*x;
a = -2;
b = 0;
tol = 10^-12;
maxIter = 100;
x=a;
for i = 1:maxIter
% Paso de Newton
if df(x) ~= 0
xk = x - f(x)/df(x);
else
xk=(a+b)/2;
end
% Verificar si el paso de Newton está dentro del intervalo
if xk <= a | xk >= b
xk=(a+b)/2;
disp('Bisección')
end
if abs(xk-x)< tol
break
end
% Se modifica el intervalo
if f(a)*f(xk) < 0
b = xk;
else
a = xk;
end
x=xk;
end
fprintf('Raíz encontrada: %.16f\n', x);
fprintf('f(raíz) = %.2e\n', f(x));
fprintf('Iteraciones: %d\n', i);
Resultado:
Raíz encontrada: -0.4832593897161711
f(raíz) = 0.00e+00
Iteraciones: 6
Canal trapezoidal
Problema:
En un canal trapezoidal, la profundidad crítica \(y_c\) satisface la ecuación:
$$ \frac{Q^2}{g} = \frac{(by + my^2)^3}{b + 2y\sqrt{1+m^2}} $$donde \(Q = 2\, m^3/s\) es el caudal, \(g = 9.81\, m/s^2\) es la gravedad, \(b = 1\, m\) es el ancho del fondo, y \(m = 1\) es la pendiente lateral. Encuentra \(y_c\).
Solución:
Compararemos los métodos de Newton-Raphson, Secante y el método de la Posición Falsa.
Q = 2; g = 9.81; b = 1; m = 1;
f = @(y) Q^2/g - (b*y + m*y^2)^3/(b + 2*y*sqrt(1+m^2));
df= @(y) (2*y^3*(b + m*y)^3*(m^2 + 1)^(1/2))/(b + 2*y*(m^2 + 1)^(1/2))^2 - (3*y^2*(b + m*y)^2*(b + 2*m*y))/(b + 2*y*(m^2 + 1)^(1/2));
% Newton-Raphson
y0 = 0.5;
tol = 1e-6;
maxIter = 100;
for i = 1:maxIter
y = y0 - f(y0)/df(y0);
if abs(y - y0) < tol
break;
end
y0 = y;
end
fprintf('Profundidad crítica (Newton): %.16f m\n', y);
fprintf('Iteraciones Newton: %d\n', i);
% Método de la Secante
y0= 0.5;
y1 = 0.6;
for i = 1:maxIter
y = y1 - f(y1)*(y1-y0)/(f(y1)-f(y0));
if abs(y - y1) < tol
break;
end
y0 = y1;
y1 = y;
end
fprintf('Profundidad crítica (Secante): %.16f m\n', y);
fprintf('Iteraciones Secante: %d\n', i);
Método de la secante
Problema:
Se considera la ecuación \(\det(A(x)) = 0\), donde \(x\) es un número real y \(A(x)\) es la matriz:
\[ A(x) = \begin{pmatrix} \cos(x) & 1 & 2 & 3 \\ 0 & 1 & 0 & 1 \\ x & 2 & 3 & 4 \\ \sin(x) & x & 1 & \cos(x) \end{pmatrix} \]
Encuentra una raíz de \(f(x) = \det(A(x)) = 0\) en el intervalo \([0, 1]\).
Solución:
Consideramos el método de la secante por la dificultad de encontrar la derivada.
f=@(x) det([cos(x), 1, 2, 3;
0, 1, 0, 1;
x, 2, 3, 4;
sin(x), x, 1, cos(x)]);
%Cambio de signo
f(0)*f(1)
% Método de la Secante
x0 = 0;
x1 = 1;
for i = 1:maxIter
x = x1- f(x1)*(x1-x0)/(f(x1)-f(x0));
if abs(x - x1) < tol
break;
end
x0 = x1;
x1 = x;
end
fprintf('Raíz (Secante): %.16f\n', x);
fprintf('f(raíz Secante) = %.16e\n', f(x));
fprintf('Iteracopmes = %d', i);
Solución:
Raíz (Secante): 1.0928624707528467
f(raíz Secante) = -6.9765478838602592e-16
Análisis de la convergencia
Problema:
Para la función \(f(x) = xe^x - 1\):
- a) Demuestra que tiene una única raíz en el intervalo \([0,1]\).
-
b) Estudia las condiciones de convergencia del método del punto fijo para las siguientes transformaciones:
- \(g_1(x) = e^{-x}\)
- \(g_2(x) = \ln(1/x)\)
- \(g_3(x) = x - \frac{xe^x - 1}{e^x + xe^x}\)
- c) ¿Cuál de estas transformaciones garantiza convergencia más rápida?
Solución:
a) Unicidad de la raíz:
Sea \(f(x) = xe^x - 1\)
- \(f(0) = -1 < 0\)
- \(f(1) = e - 1 > 0\)
- \(f'(x) = e^x + xe^x = e^x(1 + x) > 0\) para todo \(x \in [0,1]\)
Por el teorema de Bolzano, existe una raíz en \([0,1]\). Como \(f'(x) > 0\), la función es estrictamente creciente y la raíz es única.
b) Análisis de convergencia:
Para el método del punto fijo, necesitamos \(|g'(x)| < 1\) en un entorno de la raíz.
- \(g_1(x)\): \(|g_1'(x)| = |-e^{-x}| = e^{-x}\). En \([0,1]\), \(e^{-x} \in [1/e, 1]\), por lo que no garantiza convergencia en todo el intervalo.
- \(g_2(x)\): \(|g_2'(x)| = |-1/x|\). No está acotada cerca de 0, por lo que no garantiza convergencia.
- \(g_3(x)\): Esta es una iteración de Newton modificada. \(|g_3'(x)| = |\frac{(xe^x-1)^2}{(e^x + xe^x)^2}| < 1\) cerca de la raíz.
c) Velocidad de convergencia:
La transformación \(g_3(x)\) garantiza convergencia cuadrática por ser una variante del método de Newton. Es la que converge más rápidamente de las tres opciones.
% Comparación numérica de las tres transformaciones
x0 = 0.5;
tol = 1e-8;
maxIter = 100;
% g1(x)
x = x0;
for i = 1:maxIter
xk = exp(-x);
if abs(xk- x) < tol
break;
end
x = xk;
end
fprintf('g1: Iteraciones = %d, Valor = %.16f\n', i, x);
% g2(x)
x = x0;
for i = 1:maxIter
xk = log(1/x);
if abs(xk - x) < tol
break;
end
x = xk;
end
fprintf('g2: Iteraciones = %d, Valor = %.16f\n', i, x);
% g3(x)
x = x0;
for i = 1:maxIter
xk = x - (x*exp(x) - 1)/(exp(x) + x*exp(x));
if abs(xk - x) < tol
break;
end
x = xk;
end
fprintf('g3: Iteraciones = %d, Valor = %.16f\n', i, x);
Resultado:
- g1: Converge muy lentamente con el valor x0=0.5, para otros puntos puede no converger
- g2: Diverge
- g3: Converge en 4 iteraciones a 0.56714329
Método de la secante
Problema:
Utiliza el método de la secante para resolver \(f(x) = 100x^5 - 3995x^4 + 79700x^3 - 794004x^2 + 3160075x - 0\) en el intervalo \([17, 22.2]\) con un error absoluto y relativo de \(10^{-7}\). Realiza los cálculos considerando como puntos iniciales \(x_0 = 17\) y \(x_1 = 22.2\).Observad que no converge. Sin embargo sí lo hace si se considera \(x_0 = 22.2\) y \(x_1 = 17\).
Solución:
Aplicaremos el método de la secante y verificaremos tanto el error absoluto como el relativo.
% Definición de la función polinómica
f = @(x) 100*x.^5 - 3995*x.^4 + 79700*x.^3 - 794004*x.^2 + 3160075*x;
% Valores iniciales
x0 = 22.2;
x1 = 17;
tol_abs = 1e-7;
tol_rel = 1e-7;
maxIter = 100;
fprintf('Iteración\t x\t\t Error Abs\t Error Rel\n');
fprintf('----------------------------------------------------\n');
for i = 1:maxIter
% Método de la secante
x2 = x1 - f(x1)*(x1-x0)/(f(x1)-f(x0));
% Cálculo de errores
error_abs = abs(x2 - x1);
error_rel = abs((x2 - x1)/x2);
fprintf('%d\t\t %.8f\t %.2e\t %.2e\n', i, x2, error_abs, error_rel);
% Criterio de parada
if error_abs < tol_abs && error_rel < tol_rel
break;
end
% Actualización para la siguiente iteración
x0 = x1;
x1 = x2;
end
fprintf('\nSolución final: %.10f\n', x2);
fprintf('Error absoluto final: %.2e\n', error_abs);
fprintf('Error relativo final: %.2e\n', error_rel);
fprintf('Iteraciones realizadas: %d\n', i);
% Verificación del resultado
fprintf('\nVerificación: f(x) = %.2e\n', f(x2));
Resultado:
Solución final: 17.8463651211
Error absoluto final: 1.37e-08
Error relativo final: 7.68e-10
Iteraciones realizadas: 26
Verificación: f(x) = 0.00e+00
Presión de un gas
Problema:
Utiliza el método de Maehly para hallar todas las soluciones de las siguientes ecuaciones:
- \(x^6 + 3x^5 - 28x^4 + 8x^3 - 8x^2 + 4 = 0\)
- \(x^7 + 26x^6 - 54x^5 - 27x^4 + 128x^3 - 576x^2 + 864x - 432 = 0\)
- \(x^4 - 12x^3 + 47x^2 - 60x + 24 = 0\)
¿Cuántas raíces tiene cada ecuación? Comprueba los resultados con el comando
roots de Matlab.
Solución:
Escribimos la solución utilizando el comando roots de Matlab/Octave. Para aplicar método de Maehly ver los ejemplos resueltos en el tema.
% Para p1(x) = x^6 + 3x^5 -28x^4 + 8x^3 -8x^2 + 0 x + 4:
p1 = [1, 3, -28, 8, -8, 0, 4];
r1 = roots(p1)
% Para p2(x) = x^7 + 26x^6 -54x^5 -27x^4 +128x^3 -576x^2 +864x -432:
p2 = [1, 26, -54, -27, 128, -576, 864, -432];
r2 = roots(p2)
% Para p3(x) = x^4 -12x^3 +47x^2 -60x +24:
p3 = [1, -12, 47, -60, 24];
r3 = roots(p3)
Solución:
r1 =-7.1152 + 0.0000i
3.8568 + 0.0000i
0.5769 + 0.0000i
0.0753 + 0.7300i
0.0753 - 0.7300i
-0.4691 + 0.0000i
r2 =
-27.8943 + 0.0000i
-2.3739 + 0.0000i
2.2901 + 0.0000i
0.1085 + 1.7735i
0.1085 - 1.7735i
0.8805 + 0.3563i
0.8805 - 0.3563i
r3 =
5.0558 + 1.2067i
5.0558 - 1.2067i
1.0000 + 0.0000i
0.8883 + 0.0000i