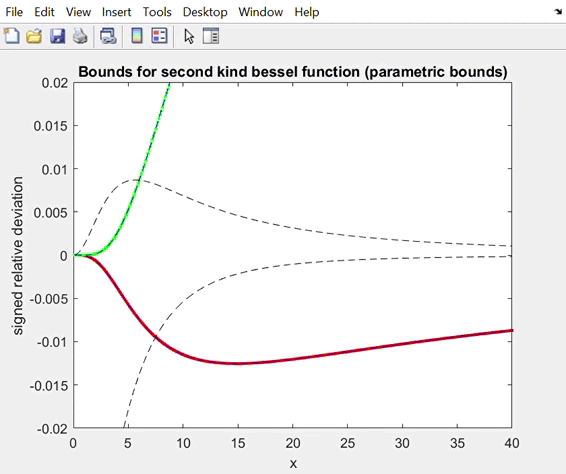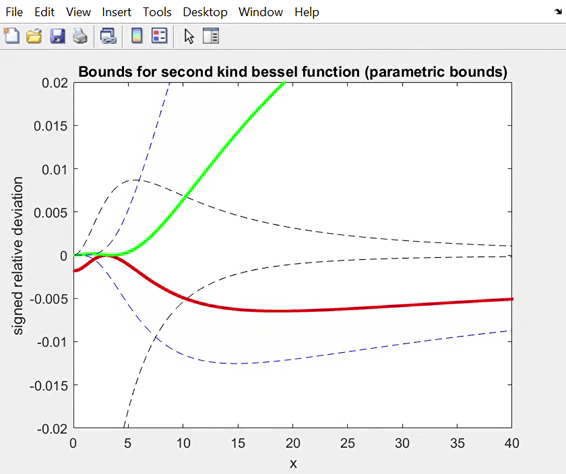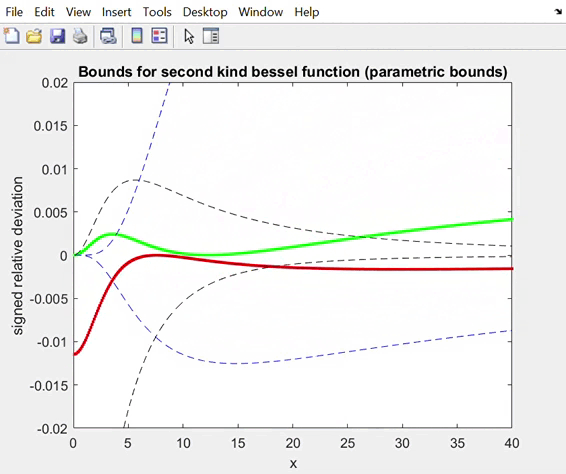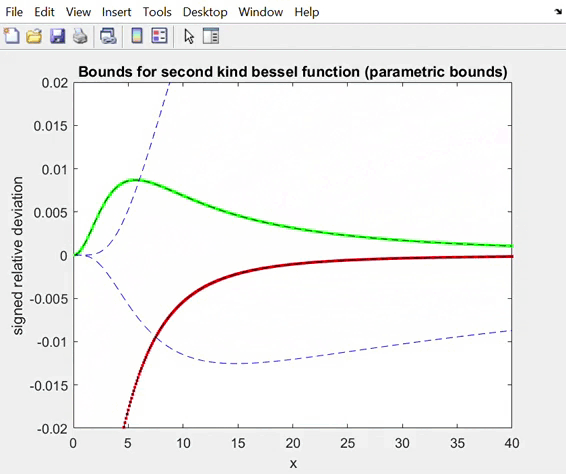
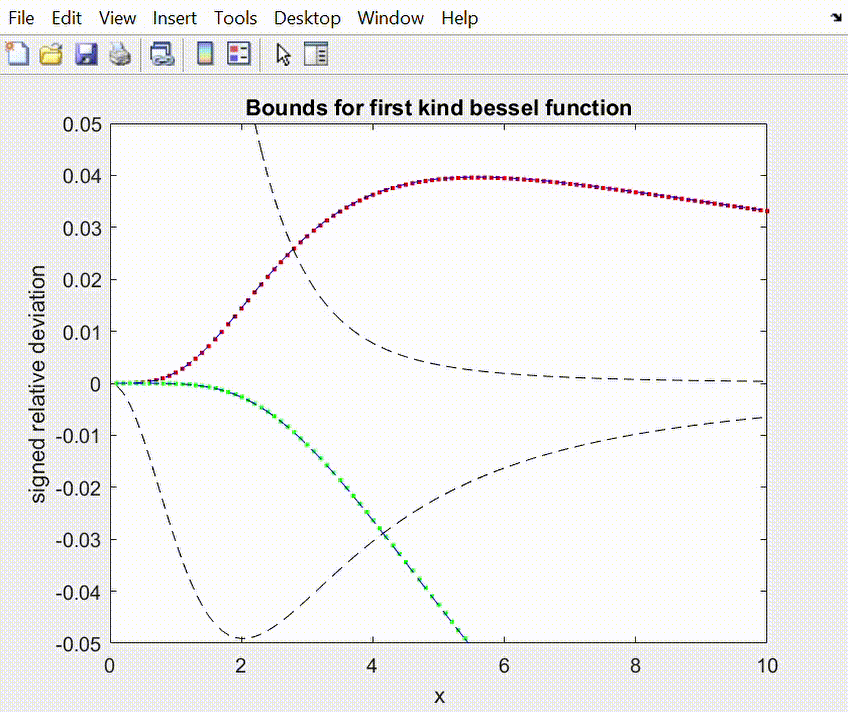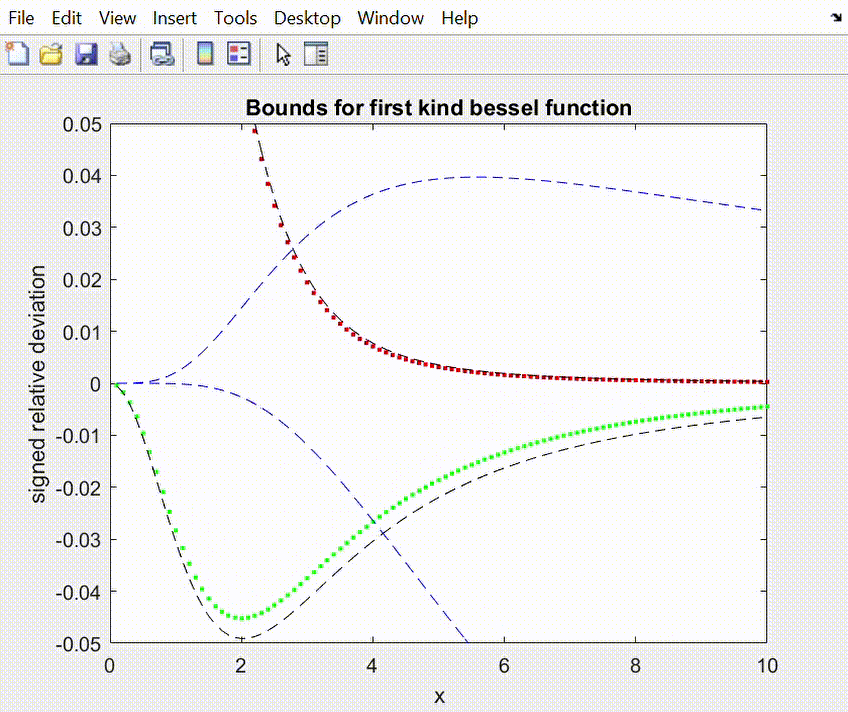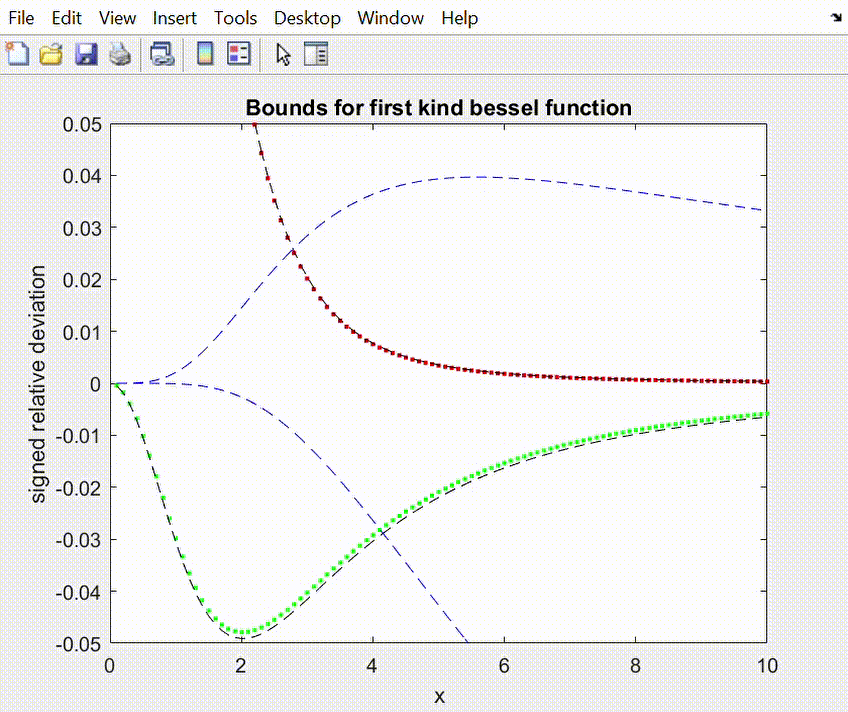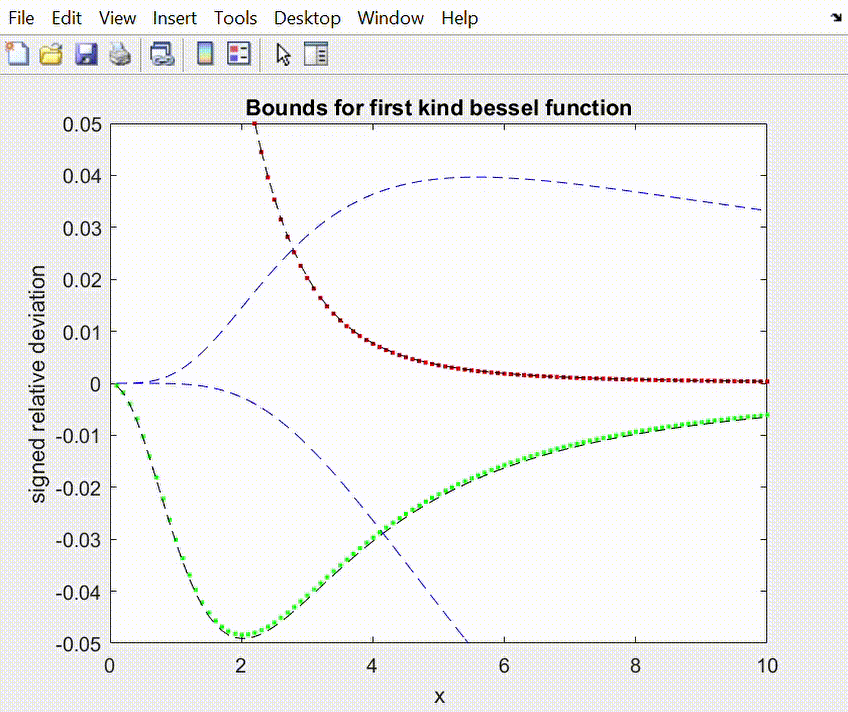
Relative deviation for the lower and upper best bounds with respect to the ratio of first kind Bessel functions.

We represent the relative deviation (R – B)/B with R the ratio of Bessel functions and B the bound. R=I_n(x)/I_n-1(x), n=0.95

From left to right:

1. Osculatory (best) bounds with the osculatory point running from 0 to +infinity. Initially the best lower (red) and upper (green) bounds coincide with the best posible bounds at x=0, and they approach to the best bounds at +infinity as the tangency points moves to the right.

2. Same as before, but with a faster speed of movement of the tangency point.

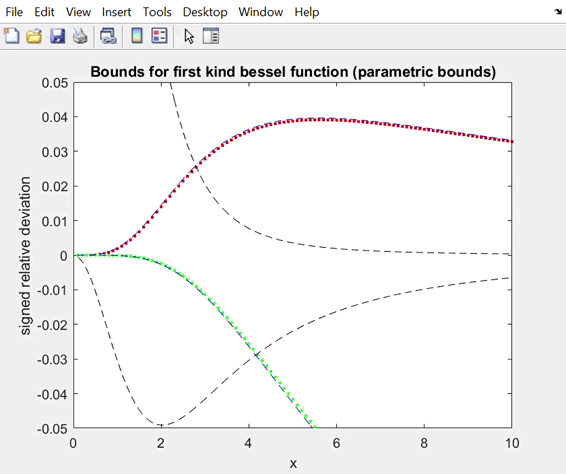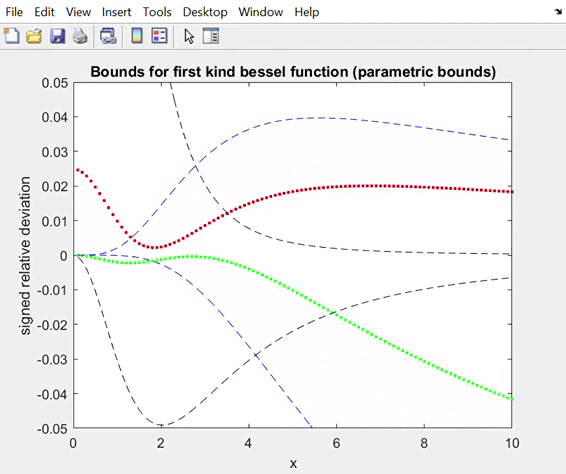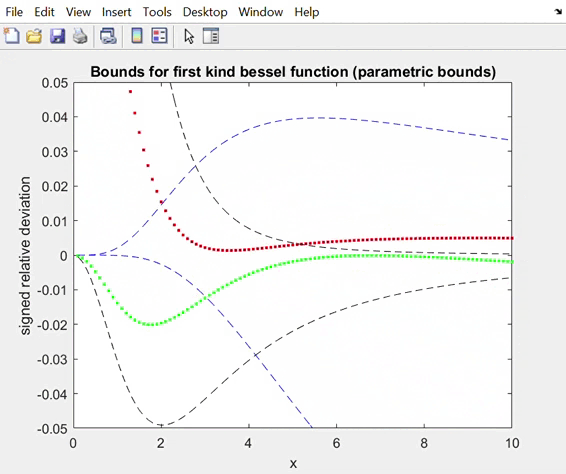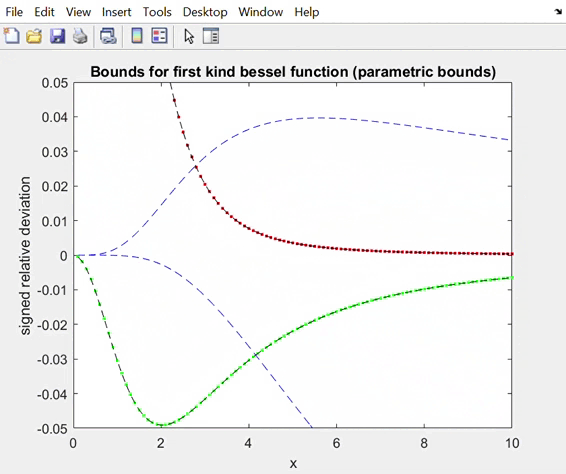
3. Approximations to the best osculatory bounds by parametric bounds. Notice that the parameters for the upper and lower bounds are not “synchronized”.

Below, we show the analogous results for second kind Bessel functions R=K_n+1(x)/K_n(x), n=5