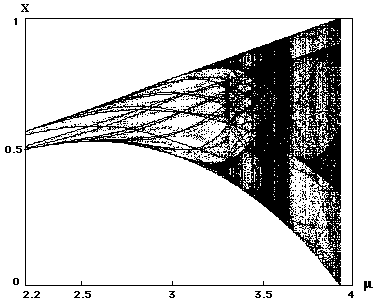
Bifurcation diagrams and invariant densities are computed and interpreted for a Logistic map driven by Dichotomic Noise. Two deterministic limits are analyzed. Changes in the stability of such a system when varying the correlation time of the noise are numerically studied. Peaks of the invariant density in the white noise case are identified as originating from most stable attractors among those appearing in the deterministic limits.
The influence of noise on discrete dynamical systems has been investigated from several points of view. There are several investigations where the shift, broadening and suppression of bifurcations have been analysed [1]. Others deal with the scaling of Lyapunov exponents and invariant densities near the onset of chaos (see [2,3]). Most of these effects have been investigated with a Gaussian white noise with small intensity. The noise acts as a perturbation of the original system and obviously their effects must be related with changes on this system.
In this paper, we consider a different kind of noise acting on discrete systems. Instead of a Gaussian white noise, we deal with multilevel processes with arbitrary intensity and correlation time.
A colored noise with sufficient intensity can induce dramatic effects on the original attractors, changing their character or creating new ones. These changes can be produced by randomness and by memory effects. Changes due only to memory effects on a Logistic map have been reported in a recent paper (see [4]). In fact, the bifurcation scenario found in the afore-mentioned paper is rather similar to our scenario for some values of the correlation time. Changes due to colored noise have been extensively studied in continuous systems with Gaussian or Markovian noise but only a few works are devoted to maps. It is worth remarking on the recent work of Ref(5), analyzing the noise induced transitions in a class of bistable oscillators driven by dichotomous noise. As pointed out in this paper, a dichotomic noise is a good candidate for studying such a complicated problem. As is well known from the study of one-dimensional stochastic continous models (see [6]), the simplicity of this noise allows one to derive analytical expressions for the probability density or transition rates for some nonlinear models. We show that also, in discrete systems with dichotomic noise, one is able to derive analytical results.
The following figure shows a bifurcation diagram of the Logistic map driven by a dichotomic noise.

References: 1. S.J. Linz and M. Lucke, Phys. Rev. A33, 2694 (1986).
2. J. Crutchfield, M. Nauenberg and J. Rudnick, Phys. Rev. Lett 46, 933 (1981);
B. Shraiman, C.E. Wayne and P.C. Martin, Phys. Rev. Lett 46, 935 (1981).
3. P. Reimann and P. Talkner, Helv. Phys. Acta 64, 946 (1991);
R. Graham, A. Hamm and T. Tel, Phys. Rev. Lett 66, 3089 (1991).
4. E. Fick, M. Fick, G. Hausmann, Phys. Rev. A44, 2469 (1991).
5. A. J. Irwin, S. J. Fraser and R. Kapral, Phys. Rev. Lett. 64, 2343 (1990);
S. J. Fraser and R. Kapral, Phys. Rev. A45, 3412 (1992).
6. C. Van den Broeck and P. Hanggi, Phys. Rev. A30, 2730 (1984);
J. Masoliver, K. Lindenberg and B. West, Phys. Rev. A33, 2177 (1986);
M. A. Rodriguez and L. Pesquera, Phys. Rev. A34, 4532 (1986).
7. J.M. Gutiérrez, A. Iglesias, M.A. Rodríguez, in "Second Granada Lectures in Computational Physics'', World Scientific.
8. L. Schimansky-Geier, H. Herzel, "Positive Lyapunov Exponents in Kramers Oscillaror". Preprint.
9. T. Kapitaniak, "Chaos in systems with noise". World Scientific, (1990) and references included therein.
10. J.M. Sancho, in "Stochastic Processes Applied to Physics". World Scientific, (1984), p. 96.