The paper presents a new efficient method for uncertainty propagation in discrete Bayesian networks in symbolic, as opposed to numeric, form, when considering some of the probabilities of the Bayesian network as parameters. The algebraic structure of the conditional probabilities of any set of nodes, given some evidence, is characterized as ratios of linear polynomials in the parameters. We use this result to carry out these symbolic expressions efficiently by calculating the coefficients of the polynomials involved, using standard numerical algorithms. The numeric canonical components method is proposed as an alternative to symbolic computations, gaining in speed and simplicity. It is also shown how to avoid redundancy when calculating the numeric canonical components probabilities using standard message-passing methods. The canonical components can also be used to obtain lower and upper bounds for the symbolic expression associated with the probabilities. Finally, we analyze the problem of symbolic evidence, which allows answering multiple queries regarding a given set of evidential nodes. In this case, the algebraic structure of the symbolic expressions obtained for the probabilities are shown to be ratios of non-linear polynomial expressions. Then we can perform symbolic inference with only a small set of symbolic evidential nodes. The methodology is illustrated by examples.
Bayesian networks are powerful tools both for graphically representing the relationships among a set of variables and for dealing with uncertainties in expert systems. A key problem in Bayesian networks is evidence propagation, that is, obtaining the posterior distributions of variables when some evidence is observed. Several efficient methods for propagation of evidence in Bayesian networks have been proposed in recent years. Exact methods exploit the independence structure contained in the network to efficiently propagate uncertainty (see, for example, Kim and Pearl (1983), Lauritzen and Spiegelhalter (1988), Jensen, Olesen, and Andersen (1990), Pearl (1988), and Shachter, Andersen, and Szolovits (1994)). Stochastic simulation constitute an interesting alternative in highly connected networks, where exact algorithms may become inefficient (Pearl (1986), Henrion (1988), Shachter and Peot (1990a), Fung and Chang (1990), Bouckaert, Castillo, and Gutiérrez (1996)). Recently, search-based approximation algorithms, which search for high probability configurations through a space of possible values, have emerged as an alternative to the above methods in special cases as, for example, in Bayesian networks with extreme probabilities (Poole (1993), Santos and Shimony (1994), Li and D'Ambrosio (1995)).
However, all exact and approximate methods require that the joint probabilities of the nodes be specified numerically, that is, all the parameters must be assigned numeric values. In practice, exact numeric specification of these parameters may not be available or it may happens that the subject matter specialists can specify only ranges of values for the parameters rather than their exact values. In such cases, there is a need for symbolic methods which are able to deal with the parameters themselves, without assigning them numeric values. Symbolic propagation leads to solutions which are expressed as functions of the parameters in symbolic form. Thus, the answers to general queries can be given symbolically in terms of the parameters and the answers to specific queries can then be obtained by plugging the values of the parameters in the solution which is given in symbolic form, without need to redo the propagation. Furthermore, symbolic propagation allows one to study the sensitivity of the results to changes in parameter values with little additional computational effort.
Recently, two main approaches have been proposed for symbolic inference in Bayesian networks. The symbolic probabilistic inference algorithm (SPI) (Shachter, D'Ambrosio, and DelFabero (1990b), Li and D'Ambrosio (1994)) is a goal directed method which performs only those calculations that are required to respond to queries. Symbolic expressions can be obtained by postponing evaluation of expressions, maintaining them in symbolic form. On the other hand, Castillo, Gutiérrez and Hadi (1995a, 1995b, 1996) perform symbolic calculations using slightly modified versions of standard numerical propagation algorithms by first replacing the values of the initial probabilities by symbolic parameters, then using computer packages with symbolic computational capabilities (such as, Mathematica and Maple) to propagate uncertainty. As opposed to SPI algorithm, this method is not goal oriented, but allows us to obtain symbolic expressions for all the nodes in the network.
However, both methods suffer from the same problem: they need to use special programs, or extra computational efforts implementing the necessary code, to carry out the symbolic computations. Furthermore, computing and simplifying symbolic expressions is a computationally expensive task, and it becomes increasingly inefficient when dealing with large networks, or large numbers of symbolic parameters. In this paper we present an efficient approach to symbolic propagation that takes advantage of the polynomial structure of the probabilities of the nodes to avoid symbolic computations. The main idea of the method is obtaining the symbolic expressions through a numerical algorithm to compute the coefficients of the associated polynomials. Then, all the computations are carried out numerically, avoiding the use of the computationally expensive symbolic manipulations. The main findings of this paper are the following:
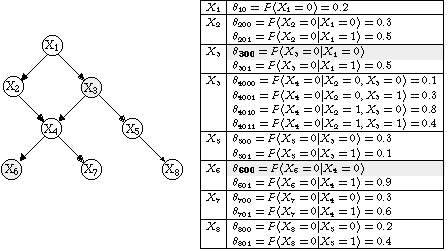
For example, consider the following Bayesian network defined using some symbolic parameters:

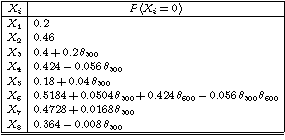
References: