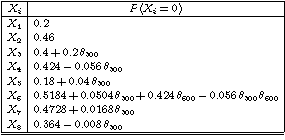Probabilistic Reasoning and Bayesian Networks
Expert systems and uncertainty in artificial intelligence have seen a great surge of research activity during the last decade. Bayesian networks are powerful tools both for graphically representing the relationships among a set of variables and for dealing with uncertainties in expert systems (see Pearl (1988) or Castillo, Gutiérrez, and Hadi (1997) for an introduction to this field). A key problem in Bayesian networks is evidence propagation, that is, obtaining the posterior distributions of variables when some evidence is observed. Several efficient methods for propagation of evidence in Bayesian networks have been proposed in recent years. Exact methods exploit the independence structure contained in the network to efficiently propagate uncertainty (see, for example, Kim and Pearl (1983), Lauritzen and Spiegelhalter (1988), Jensen, Olesen, and Andersen (1990), Pearl (1988), and Shachter, Andersen, and Szolovits (1994)). Stochastic simulation constitute an interesting alternative in highly connected networks, where exact algorithms may become inefficient (Pearl (1986), Henrion (1988), Shachter and Peot (1990a), Fung and Chang (1990), Bouckaert, Castillo, and Gutiérrez (1996)). Recently, search-based approximation algorithms, which search for high probability configurations through a space of possible values, have emerged as an alternative to the above methods in special cases as, for example, in Bayesian networks with extreme probabilities (Poole (1993)).
However, all exact and approximate methods require that the joint probabilities of the nodes be specified numerically, that is, all the parameters must be assigned numeric values. In practice, exact numeric specification of these parameters may not be available or it may happens that the subject matter specialists can specify only ranges of values for the parameters rather than their exact values. In such cases, there is a need for symbolic methods which are able to deal with the parameters themselves, without assigning them numeric values. Symbolic propagation leads to solutions which are expressed as functions of the parameters in symbolic form. Thus, the answers to general queries can be given symbolically in terms of the parameters and the answers to specific queries can then be obtained by plugging the values of the parameters in the solution which is given in symbolic form, without need to redo the propagation. Furthermore, symbolic propagation allows one to study the sensitivity of the results to changes in parameter values with little additional computational effort.
Recently, two main approaches have been proposed for symbolic inference in Bayesian networks. The symbolic probabilistic inference algorithm (SPI) (Shachter, D'Ambrosio, and DelFabero (1990), Li and D'Ambrosio (1994)) is a goal directed method which performs only those calculations that are required to respond to queries. Symbolic expressions can be obtained by postponing evaluation of expressions, maintaining them in symbolic form. On the other hand, Castillo, Gutiérrez and Hadi (1996) perform symbolic calculations using slightly modified versions of standard numerical propagation algorithms by first replacing the values of the initial probabilities by symbolic parameters, then using computer packages with symbolic computational capabilities (such as, Mathematica and Maple) to propagate uncertainty. As opposed to SPI algorithm, this method is not goal oriented, but allows us to obtain symbolic expressions for all the nodes in the network.
However, both methods suffer from the same problem: they need to use special programs, or extra computational efforts implementing the necessary code, to carry out the symbolic computations. Furthermore, computing and simplifying symbolic expressions is a computationally expensive task, and it becomes increasingly inefficient when dealing with large networks, or large numbers of symbolic parameters. Castillo, Gutiérrez and Hadi (1996) present an efficient approach to symbolic propagation that takes advantage of the polynomial structure of the probabilities of the nodes to avoid symbolic computations. The main idea of the method is obtaining the symbolic expressions through a numerical algorithm to compute the coefficients of the associated polynomials. Then, all the computations are carried out numerically, avoiding the use of the computationally expensive symbolic manipulations.
For example, consider the following Bayesian network defined using some symbolic parameters:
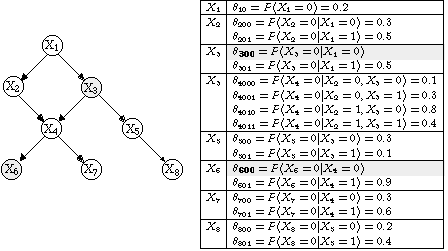
The symbolic marginal probabilities of the nodes obtained by using the above symbolic method are