Estos contenidos están protegidos © Alberto González Díez, 27-01-2015.
Umbrales de precipitación
¿Cuál es la precipitación o intensidad de lluvia mínima requerida para producir roturas en laderas?
La experiencia señala que los umbrales de lluvia pueden cambiar de una región a otra. Por ejemplo, se han citado en la literatura roturas con umbrales de precipitación muy diferentes, así:
•precipitaciones de 200 mm en 24 horas producen deslizamientos inminentes (Bhandari et al., 1991).
•En Hong Kong se han originado “debris flows” con 70 mm de precipitación (Brand, 1985, Au, 1998)
•En Hawai, se requieren, al menos precipitaciones entre 250-300 mm (Pierson et a., 1991).
•En Cantabria 100 mm/24 h (años 1983, 1994, González, 1995).
Caine (1980), usando registros de precipitaciones locales definió un umbral máximo para la inicialización de deslizamientos de I=14.82 D-0.39
, donde I es la intensidad de precipitación medida en mm/h y D es la duración de la precipitación medida en horas. Los datos del ajuste son muy buenos entre 10 minutos y 3 días. Los datos fueron compilados para una gran variabilidad de condiciones geológicas y climáticas.
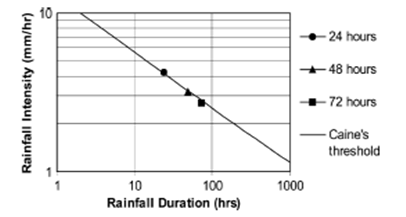
Fig. 1. Es una reproducción tomada de Shakoor y Smithmyer (2005),
en la que se muestran los umbrales de intensidad y duración de
precipitación, para tormentas que generan deslizamientos; basados en
(Caine, 1980). Esa función se ha construido usando los datos de
precipitaciones tomados a 24, 48 y 72 horas en Marietta, Ohio.
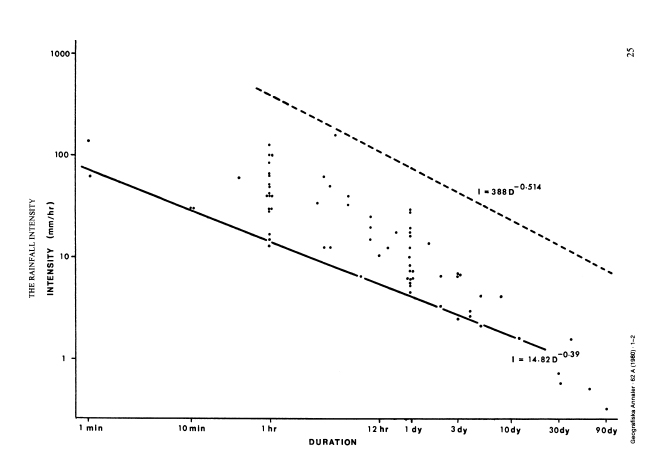
Fig. 2. Umbrales mínimo y máximo de precipitación definidos por Caine,
1980
que investigó un total de 73 deslizamientos
superficiales (<
A partir de esta idea otros autores han trabajado tratando de mejorar el conocimiento entre las relaciones existentes entre lluvias y deslizamientos. Lógicamente, las primeras fases de esta mejora provienen del análisis crítico del trabajo de Caine. Así por ejemplo, Crozier (1997) plantea que el tratamiento de los datos efectuado por Caine esta sesgado ya que no incluye eventos climáticos en los que no se hayan desarrollado deslizamientos. Efectivamente, para saber qué lluvias podrían producir deslizamientos se tienen que tomar en consideración tanto las lluvias que producen deslizamientos (lluvias efectivas) como las que no producen deslizamientos (lluvias no efectivas), teniendo en cuenta toda la información del registro climático posible. Sin embargo, es dificil encontrar registro documental de lluvias que hayan producido deslizamientos; esta tarea es más dificil si los deslizamientos se producen en zonas elevadas de las montañas que no afectan a vidas o bienes.
No obstante, justificando la aportación realizada por Caine, hay que tener presente que su intención fue la de conocer, en primera aproximación, cuál es la relación existente entre lluvias y movimientos de laderan, el se encontro con la idea del umbral al analizar los datos. Naturalmente, una vez conocida existencia de esa relación, es el momento, a partir de un correcto análisis estadístico de la información, de conocer cuál es el umbral para lluvias efectivas.
Otra crítica adicional planteada con anterioridad (González Díez et al., 2005) es que la cantidad de lluvia infiltrada necesaria para que se produzcan argayos varia de una ladera a otra, por lo tanto, el establecimiento de umbrales de precipitación en amplias zonas depende de la homogeneidad de las laderas y no tanto de las lluvias.
Tomando como base la idea inical de Caine, otros autores llevaron a cabo análisis sismilares. Cannon y Ellen (1985); Wieczoreck (1987) o Wieczoreck et al., (2000), realizaron propuestas de mayor precisión sobre el desarrollo de deslizamientos por lluvias. Estos autres proponen considrar también la lluvia antecedente además de a la intensidad-duración. La comparación de los datos demuestra la variabilidad de las condiciones hidroclimáticas responsables de la ocurrencia de deslizamientos y enfatiza que los umbrales requieren calibración para regiones específicas, dado que los valores de estos autores se sitúan sobre la línea de Caine.
Posteriormente, Shakoor y Smithmyer (2005) llevaron a cabo un tratamiento similar al de Caine pero considerando roturas en taludes construidos sobre depósitos coluviales. Estos autores encuentran valores coherentes con los de Caine (1980) con ligeras variaciones que se describen a continuación:
-
Los deslizamientos, provocados por tormentas, son fundamentalmente roturas translacionales que se originaron a lo largo del contacto entre el depósito superficial y la roca del sustrato (corresponden al modelo de talud infinito).
-
Estos movimientos se producen cuando el material tiene un porcentaje de saturación entre el 90 y 100%, dependiendo de los ángulos de la ladera. Sobre esta idea surge una línea de investigación interesante en sistemas de alerta que es la de analizar el grado de saturación de laderas con el tiempo y su comportamiento frente a lluvias intensas.
-
En estos movimientos la vegetación juega un importante papel desviándo las rotura alrededor de los árboles y arbustos.
-
Las litologías del sustrato son más propensas que el depósito superficial a sufrir deslizamientos, (Shakoor y Smithmyer, 2005).
Sin embargo, hay que tener presente que las características hidrológicas, geométricas y geotécnicas de las laderas cortadas artificialmente difieren de las naturales, por lo que no se puede extender directamente este aprendizaje.
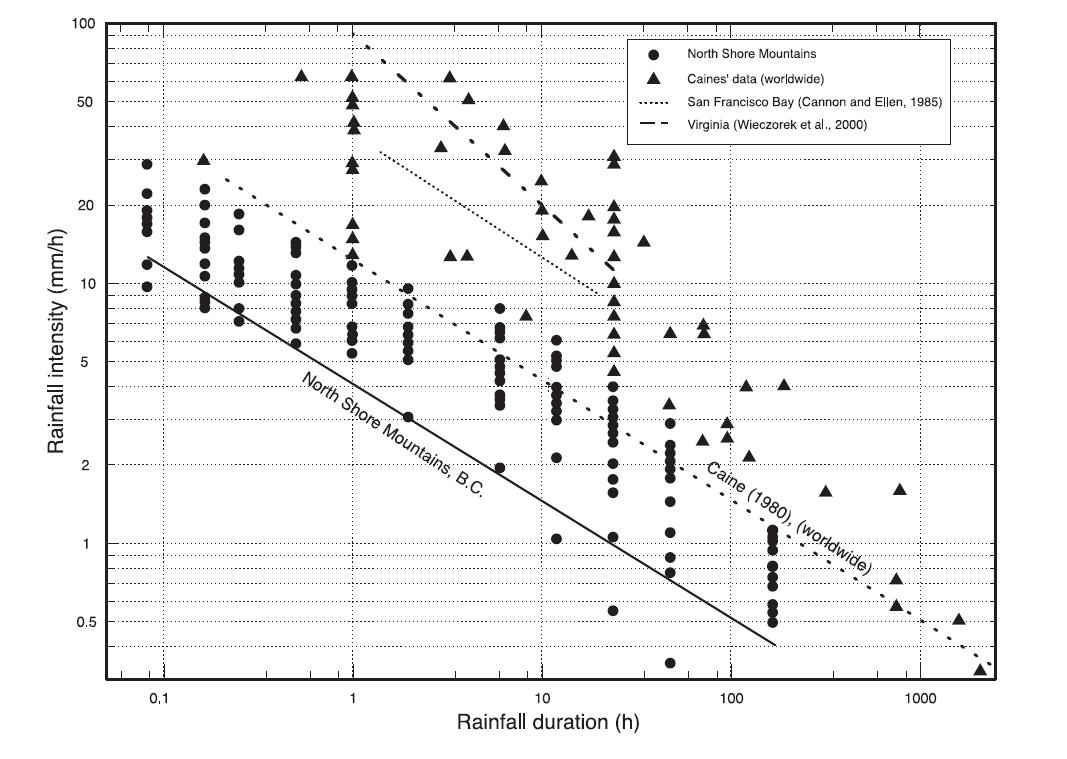
Fig. 3. Caine’s (1980) rainfall intensity– duration graph for
shallow landslides worldwide. Shallow landslides from the North
Shore Mountains of British Columbia are superimposed, as are
thresholds established for the San Francisco Bay area (Cannon
and Ellen, 1985) and the Blue Mountains of Virginia (Wieczorek
et al., 2000). Note that the majority of data points from this
study lie below Caine’s threshold, which renders it unusable for
the North Shore Mountains of Vancouver.
Sin embargo, no hay muchos estudios que permitan poder extender los análisis de Caine a nuestra región. Como ya se ha citado algunos trabajos reflejan que hay roturas con 100 mm en 24 horas, pero a veces con intensidades mucho mas reducidas (González Díez et al., 2012) se han registrado roturas.
No obstante, se podría extender el umbral propuesto por Caine, en primera aproximación, como nivel de referencia de alerta, antes de tener un nivel definido para cantabria. Un ejemplo se presenta a continuación. El pasado viernes 30 de enero de 2015, se registraron lluvias muy intensas en Cantabria que ocasionaron muchos argayos. Por ejemplo, en nuestra zona de estudio de Villafufre, se alcanzó el umbral de Caine a las 18:40. Evidentemente, si ese umbral se sobrepasa debe de comenzar la aparición de roturas en las laderas de la zona como así fue.
Otros autores (Guidicini y Iwasa, 1997), proponen otros
indicadores para normalizar el papel de la lluvia. De esta
namera nace el denominado coeficiente del evento, que mide la
relación existente entre el total de precipitación del evento y
la precipitación media anual. Este indicador se ha mostrado muy
útil en varios trabajos (Govi y Sorzana, 1980; Cannon y Ellen,
1988; Mark y Newman, 1988; Pierson et al. 1991). Aunque este
coeficiente varia según la zona de estudio entre 0,16 y 0,06
como señalan diversos autores (Guidicini y Iwasa, 1997; Polloni et al. 1996; Harp y Savage,
1998).
La utilización de este umbral, en primera aproximación, podría
ser de gran ayuda para la gestión del riesgo pues permite avisar
a la población y comenzar a prepararse ante lo que pueda
ocurrir.
Pero, ¿se puede ir mas allá? ¿se puede conocer más sobre estos umbrales? Un aspecto que llama la atención de la aplicación de este umbral en Cantabria es que si bien, superado el mismo, se han producido deslizamientos en muchas partes de la región, espacialmente su distribución espacial es heterogénea. No todas las laderas estaban igaulmente saturadas y han funcionado de la misma manera. Por lo tanto, las intensidades de lluvia tomadas de manera individual no son del todo apropiadas para la predicción de deslizamientos, si no van acompañadas de medidas de la humedad del antecedente que tienen los materiales que forman las laderas. Intentanto ajustar más esta idea Jacob y Weatherly (2003) proponen un sistema de alerta ante lluvias, a través de un análisis discriminante que considere todas las precipitaciones que se desarrollan en un área de estudio, produzcan o no deslizamientos (con el fin de hacer un correcto tratamiento estadístico).
Los autores obtienen una función discriminante:
CSL= -11,71+ 0,14 QM1+ 0,02 A4W+0,35
I6h
CSNL =-8,18 -0,06 QM1 + 0,01 A4W + 0,50 I6h
Donde: QM1 son los caudales medidos en estación de aforo; A4w es la lluvia antecedente 4 semanas previas a la precipitación (en mm), y I6h es la intensidad de lluvia en las últimas 6 horas (en mm).
CSL y CSNL representan las puntuaciones discriminantes para tormentas desencadenantes de deslizamientos y no desencadenantes. Si el valor CSL es mayor que la puntuación CSNL, la combinación de condiciones antecedentes y actuales son similares para desencadenar deslizamientos superficiales; si el número CSL es inferior, estas condiciones no son similares para producir deslizamientos superficiales. Las diferencias entre CSL y CSNL pueden expresarse como DCS, que es una medida directa de la posibilidad de que ocurran deslizamientos. Así, si DCS=CSL-CSNL es positiva, es probable que ocurran deslizamientos y viceversa.
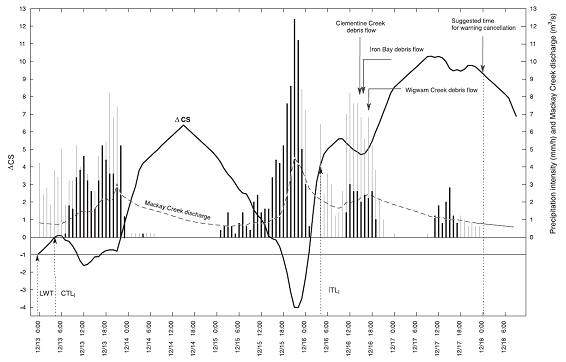
Fig. 4. Changes of DCS, rainfall intensity, and discharge at Mackay Creek during the storm of December 15 and 16, 2001. Thick vertical bars indicate unadjusted rainfall intensities at the District Hall rain gage. Thin vertical bars indicate rainfall intensities at the Seymour Falls rain gage. LWT is the landslide warning threshold, CTLI is the conditional landslide initiation threshold, and ITLI is the imminent landslide initiation threshold.
Extendiendo este concepto a la evolución de una ladera, un
cálculo continuo de DCS representa una medida integrada
hidroclimática para la probabilidad de deslizamientos en un
momento específico del tiempo que puede usarse para el diseño de
sistemas de alerta.
El problema que plantea su uso es la dispersión que pueden tener las células convectivas de alta intensidad y precipitación en el área de estudio. Una aproximación equivalente es la planteada por Aleotti (2004) Italia.
¿Se sabe algo de cuáles son las frecuencias temporales de producción de tormentas importantes en Cantabria, que hayan causado roturas en sus laderas? Ésta es una línea de conocimiento en la varios investigadores están trabajando. Parece ser que hay como dos tendencias superpuestas. Hay un registro de alta frecuencia temporal, obtenido a partir de los datos registrados por nuestras estaciones meteorológicas que distinguen cuantro periodos del año en el que se registran lluvias intensas generadoras de movimientos de ladera (1º, a finales de Enero; 2º, al principio-mediados de junio; 3º, a finales del verano; 4º, a finales de noviembre). Hay otra señal de alta frecuencia temporal que se deduce del catálogo de inundaciones históricas y mapa de riesgos potenciales del MOPU (1985), en la que se aprecia como el mes en el que aparecen mayor numero de registros altamente catastróficos es septiembre. Aunque también aparecen fenómenos en noviembre y junio-julio.
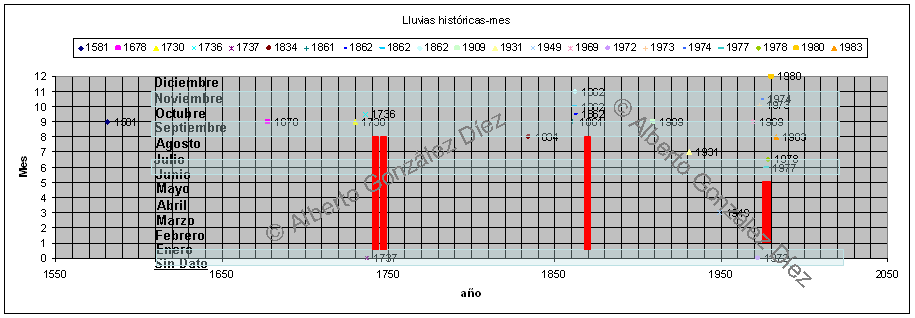
Fig. 5. Distribución temporal de las inundaciones históricas registradas en Cantabria [fuente MOPU (1985). Cuenca Norte de España. Inundaciones Históricas y Mapa de Riesgos Potenciales. (informe encargado a la Asociación de Arquitectos e Ingenieros Consultores, AICASA); en la que se han remarcado en azul claro los periodos del año más lluviosos deducidos del registro y en rojo aquellas inundaciones que ocasionaron daños notables en el relieve y que de los mismos queda constancia en archivos.
Otro aspecto igualmente importante es conocer la distribución media de la precipitación a lo largo del año. La precipitación constituye un importante agente erosivo. Es de suponer que en las zonas donde se concentra mayor intensidad de precipitación sus laderas estarán más frecuentmente saturadas y deberían estár sujetas a mayor número de deslizamientos. En 1999 se desarrolló un modelo de erosividad de la precipitación basado en el índice de Fournier (1960), Este índice está basado en la relación entre la precipitación media mensual del mes más lluvioso (pmax) y la precipitación media anual (P) IF= p2max / P.
La representación espacial de ese modelo se presenta en la Figura 6. El modelo obtenido del índice de Fournier al que se le ha superpuesto el inventario de movimientos de ladera de Cantabria (Grupo Geodinámica externa DCITIMAC, realizado a escala 1/50.000) muestra como hay una cierta relación entre la localización espacial de movimientos de ladera inventariados y la localización espacial de las lluvias mas intensas. Sin embargo, la aparición de numerosos deslizamientos fuera de las áreas de mayor IF indica que otros factores están jugando también de manera importante en la ocurrencia de deslizamientos en Cantabria, no solo la lluvia.
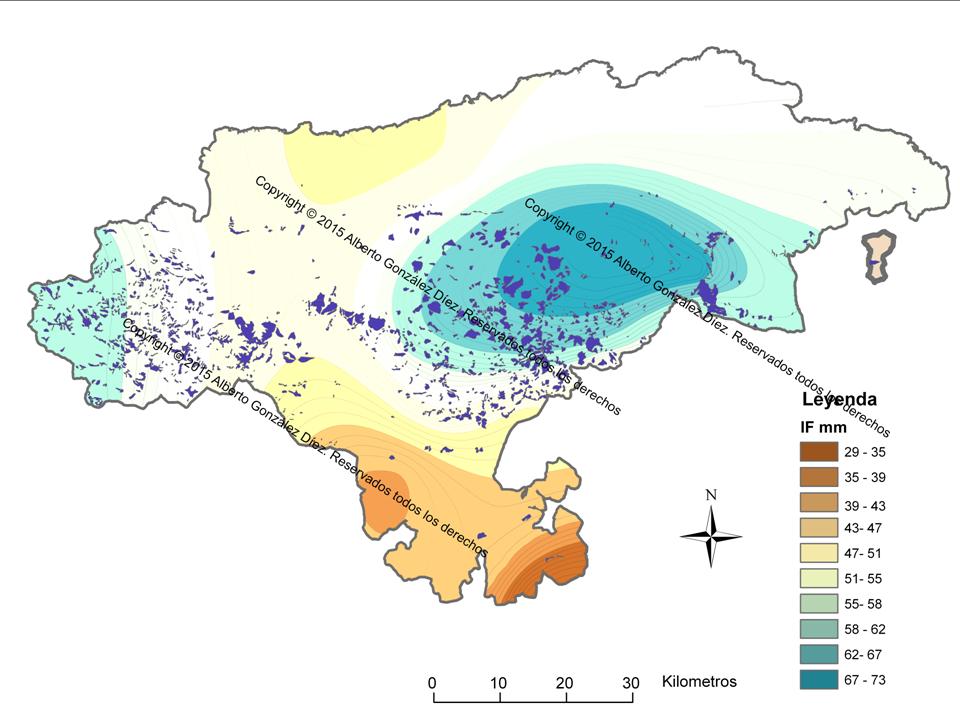
Fig. 6. Modelo de intensidad de la precipitación (basado en IF de Fournier, 1960) sobre el que se ha impreso el inventario de movimientos de ladera a escala 1/50.000 del DCTIMAC.
Bibliografía:
Aleotti, P. (2004). “Awarning system for rainfall-induced shallow failures” Engineerin Geology 73, 247-265.
Bhandari, R.K., Senanayake, K.S. & Thayalan, N. (1991). “Pitfalls in the
prediction on landslide through rainfall data”.
6th International Symposium on Landslides.
Brand, E.W. (1985). “Predicting the performance
of residual soil slopes”.
Proceedings 11th Int. Conf. Soil Mech. y Found.
Engineering.
Cannon,
Guidicini, G. & Iwasa, O. Y. (1977). “Tentative correlation between rainfall and landslides in humid tropical environment”. Bull. Int. Assoc. Eng. Geologists, 16: 13-30.
Govi, M. & Sorzana, P.F. (1980). “Landslide susceptibility as function of critical rainfall amount in Piedmont basins (North-Western Italy). Studia Geomorphologica Carpatho-Balcanica. 14: 43-61
Harp, E.L. & Savage, W.Z. (1998). “Landslides triggered by the April 1997
tropical storms on
Mark, R.K. & Newman, E.B. (1988).
“Rainfall totals before and during the storm: distribution and
correlation with damaging landslides”. En: S.D. Ellen & G.F.
Wieczorek (Eds.). “Landslides, floods and marine effects of
the storm of
Ministerio de Obras Públicas y Transportes, MOPT (1988). Las Inundaciones
en
Pierson, T.C.; Iverson, R.M. & Ellen, S.D. (1991).
“Spatial and temporal distribution of shallow landsliding during
intense rainfall, southeastern
Polloni, G.; Aleotti, P.; Baldelli, P. & Nosetto, A.
(1996).
“Heavy rain triggered landslides in the Alba area
during November 1994 flooding event in the Piemonte Region (
Shakoor A. & Smithmyer A.J. (2005). “An analysis
of storm-induced landslides in colluvial soils overlying mudrock
sequences, southeastern
Jakob, M. & Weatherly, H. (2003). “A hydroclimatic
threshold for landslide initiation on the
Wieczorek, G.F. (1987). “Effect of rainfall intensity and duration on
debris flows in central
Wieczorek, G.F. (1996). “Landslide triggering mechanisms”. En: A.K.
Turner & R.L. Schuster (Eds.) “Landslides: investigation and
mitigation”. TRB Special Report, 247.
Wieczorek, G.F. & Jäger, S. (1996).
“Triggering mechanisms and depositional rates of postglacial
slope-movement processes in the Yosemite Valley,
Wieczorek, G.F., Morgan, B.A.,
Se está actualizando
 |
LA
CIENCIA SE COMPONE DE ERRORES, QUE A SU VEZ, SON LOS PASOS HACIA LA VERDAD ‹Julio Verne› |
Pensar, es facil. Actuar
es un poco mas dificil. Pero actuar como pensamos es mucho mas dificil. (Johann Wolfgang von Goethe). |
Los procesos terrestres externos no solamente aportan información del funcionamiento interno del planeta, sino también de la actividad del sol y de la influencia del hombre
Inicio-Home |
Perfil-Profile |
documentación-documentation |
Mapa de la web-Web_map
Copyright © 2015 Alberto González Díez. Reservados todos los derechos.