Chequeo de tipos

1 Aumentando los árboles de sintaxis

La forma de aumentar la capacidad expresiva de los árboles de derivación es añadir información en los nodos, mientras se recorre el árbol en profundidad.

2 Aumentando los árboles de sintaxis

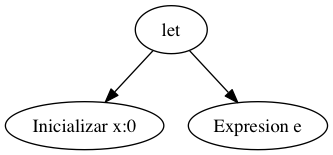
AST.png

Figura 1: Ejemplo de AST let x: Int <- 0 in e

3 Tablas de símbolos

Una tabla de símbolos es una estructura que permite almacenar, eliminar y consultar de forma eficiente símbolos definidos en un programa. Tiene las siguientes operaciones:

  • add-symbol(x)
  • remove-symbol()
  • find-symbol(x)

4 Tablas de símbolos

Añadimos dos operaciones a la tabla de símbolos:

  • enter-scope()
  • add-symbol(x)
  • find-symbol(x)
  • check-scope(x)
  • exit-scope()

5 Tipos

Si tenemos la siguiente porción de código de ensamblador: 

add $r1 ,$r2, $r3

¿Qué tipos tienen los registros?

6 Chequeo de tipos

El objetivo del chequeo de tipos es comprobar que todos los métodos que se utilizan en un programa utilizan los tipos correctos.

  • Chequeo estático.
  • Chequeo dinámico.

7 Chequeo de tipos

  • Chequeo estático.
    • Es más rápido ejecutandose.
    • No hay que preocuparse de errores cuando se ejecuta el programa.
  • Chequeo dinámico.
    • Es más fácil realizar prototipos.
    • Requieren restringir los programas.

8 Tipos en cool

  • Hay dos tipos: SELF-TYPE y las clases.
  • El usuario declara el tipo de cualquier identificador.
  • El compilador deduce el tipo de cualquier expresión.

9 Lógica para los tipos

\begin{eqnarray*} &\vdash& e_2:Int\\ &\vdash& e_1:Int\\ \hline &\vdash& e_1+e_2:Int \end{eqnarray*}

10 Lógica para los tipos

\begin{eqnarray*} &\vdash& \text{ e es un entero}\\ \hline &\vdash& e:Int \end{eqnarray*}

11 Pregunta

Demostrar que \(1+2*3\) tiene tipo \(INT\), añadiendo las reglas necesarias.

12 Lógica para los tipos

Un conjunto de reglas para la inferencia de tipos tiene la propiedad de solidez si, cada vez que se deduce un tipo, entonces el objeto tiene ese tipo para cualquier entrada.

13 Lógica para los tipos

\begin{eqnarray*} &\vdash& \text{ e es un entero}\\ \hline &\vdash& e:Object \end{eqnarray*}

14 Lógica para los tipos

\begin{eqnarray*} \\ \hline &\vdash& false:Boolean \end{eqnarray*}
\begin{eqnarray*} \\ \hline &\vdash& new\ T:T \end{eqnarray*}

15 Lógica para los tipos

\begin{eqnarray*} &\vdash& e1:Boolean\\ &\vdash& e2:T\\ \hline &\vdash& while\ e1\ loop\ e2\ pool:Object \end{eqnarray*}

16 Lógica para los tipos

Si \(x\) es el nombre de la variable, y tenemos que ponerle tipo, ¿cual es la regla que debemos escribir?

17 Ambiente de tipos

Un ambiente de tipos (type environment) es una estructura que da tipos a las variables libres.

18 Ambiente de tipos

Sea \(O\) una estructura de datos que, a cada identificador devuelve el tipo del objeto.

Utilizaremos la siguiente notación:

\begin{eqnarray*} &O\ \vdash& e: T \end{eqnarray*}

19 Ambiente de tipos (nuevas reglas)

\begin{eqnarray*} &O(x) =& T\\ \hline &O\ \vdash& x: T \end{eqnarray*}
\begin{eqnarray*} &O(T0/x)\ \vdash& e1: T\\ \hline &O\ \vdash& let\ x:T0:\ e1: T1 \end{eqnarray*}