Tablas de parsing

1 Representación de las tablas de parsing

\begin{eqnarray*} N &:& D\ |\ N\ D\\ D &:& 0\ |\ 1\ |\ 2\ |\ 3\ |\ 4\ |\ 5\ |\ 6\ |\ 7\ |\ 8\ |\ 9 \end{eqnarray*}

	dígito	$
€	desplazar
digito	reducir a D	reducir a D
€N	desplazar	aceptar
ND	reducir por N: ND	reducir por N: ND
€D	reducir por N: D	reducir a N:D

2 ¿Por qué funcionan los analizadores LR?

Un analizador sintáctico acepta una entrada si y solamente si la entrada se puede generar por la gramática.

El analizador LR aceptará si y solamente si en la pila tenemos el euro, la variable inicial y el fin de datos.

3 Problemas con las tablas de parsing

¿Cómo queda el algoritmo LR en general?
¿Qué pasa cuando hay una λ-producción?
¿Qué pasa cuando el autómata con pila no es determinista?

4 ¿Qué pasa cuando hay una λ-producción?

\begin{eqnarray*} S &:& (S)S \mid \lambda \end{eqnarray*}

En esta gramática, ¿cuando hay que reducir por la λ-producción?

5 Prefijo viables

Para cada regla de la gramática: Hemos de decidir cuándo conviene usarla para reducir, es decir,

sabiendo ``lo que hay en la pila'',
y sabiendo cuál es el próximo símbolo de la entrada,

saber si hemos de reducir por esa regla o no.

Consideramos un paso intermedio de la derivación derecha: ¿qué es necesario conocer para saber cuál fue el paso anterior?

La dificultad es cuando tenemos ambigüedad y que haya varios candidatos al paso anterior.

6 Definición de prefijo viable

Dada una gramática libre de contexto, se dice que

$\alpha\beta_1\in\{V\cup \Sigma \}^*$

es un prefijo viable si

\begin{eqnarray*} S\mapsto_{rm}\ldots \mapsto_{rm}\alpha A\omega\mapsto_{rm}\alpha\beta_1\beta_2\omega \end{eqnarray*}

7 Idea del LR

La idea del análisis ascendente expresada de otra forma es:

leer la palabra de izquierda a derecha,
encontrar el mayor prefijo viable,
reducir cuando en el próximo símbolo deje de ser prefijo viable.

8 Identifiquemos los prefijos viables en un caso práctico

(Omitimos las reducciones de dígito, operador y de numero para mayor claridad)

E
E OP E
E OP E OP E
E OP E OP 3
E OP E + 3
E OP 2 + 3
E * 2 + 3
1 * 2 + 3

9 Identifiquemos los prefijos viables en otro caso práctico

Tomamos la siguiente gramática

\begin{eqnarray*} T &:& S ;\\ S &:& S A\ \mid\ A\\ A &:& (A)\ \mid\ ()\\ \end{eqnarray*}

La derivación a la izquierda de la palabra () (()) ; es \[T \mapsto S ; \mapsto S A ; \mapsto S (A) ; \mapsto S (()) ; \mapsto A (()) ; \mapsto () (()) ; \]

¿Cuales son aquí los prefijos viables?

10 La clave de boveda

Todo lenguaje libre de contexto determinista, en el que ninguna palabra sea prefijo de otra, admite una gramática en la cual el conjunto de prefijos viables para cada regla es un lenguaje regular.

11 La clave de boveda

Como siempre tendremos una marca de fin, en la práctica nunca una palabra aceptada es prefijo de otra.

12 La clave de boveda

Consecuencia: Para cada regla, existe un autómata finito que puede recorrer la pila y decirnos si hay que reducir usándola. Podemos combinarlos todos en uno solo, que recorre la pila y nos indica si hay que reducir o no, y cuál es la regla para utilizar.

13 Items LR(0)

Dada una gramática libre de contexto, un ítem LR(0) es un par formado por una regla de la gramática y un número natural entre 0 y la longitud de la parte derecha.

14 Items LR(0)

Lo escribimos con frecuencia entre corchetes. Cuando el número sea i, en vez de escribirlo explícitamente, pondremos un punto a continuación del i-ésimo símbolo de la parte derecha.

Por ejemplo, esto es un item LR(0) representando la regla \[A\mapsto AA,\ i = 1,\]

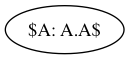
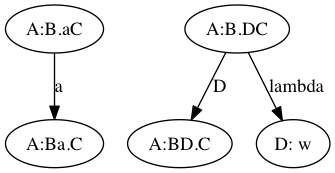
15 Autómata LR(0) (versión indeterminista)

Estados: todos los ítems LR(0).
Estado inicial:

Estados finales: todos los items LR(0) donde el punto este al final de la regla.
Transiciones de dos tipos: