Clases y herencia
1 Estudio de let con inicialización
Dado este código
let x: T0 <- e0 in e1
Tenemos que deducir el tipo del objeto:
\begin{eqnarray*}
&O(T0/x)\ \vdash& e1: T\\
&O\ \vdash& e0: T0\\
\hline
&O\ \vdash& let\ x:\ T0\ <- e0\ in\ e1: T
\end{eqnarray*}
2 Subtipos
Un orden parcial en una jerarquía de tipos es una relación binaria \(\le\) tal que cumple:
- \(X\le X\)
- \(X\le Y\) si \(X\) es un subtipo de \(Y\)
- Si \(X\le Y\) y \(Y\le Z\) entonces \(X\le Z\)
3 Subtipos
\begin{eqnarray*}
&O(T0/x)\ \vdash& e1: T\\
&O\ \vdash& e0\ : T1\\
&& T1\le T0\\
\hline
&O\ \vdash& let\ x:\ T0\ <- e0\ in\ e1: T
\end{eqnarray*}
4 Subtipos
\begin{eqnarray*}
&& O(x) = T0\\
&O\ \vdash& e0\ : T1\\
&& T1\le T0\\
\hline
&O\ \vdash& x <- e0: T1
\end{eqnarray*}
5 Subtipos
\begin{eqnarray*}
&& O_C(x) = T0\\
&O\ \vdash& e0\ : T1\\
&& T1\le T0\\
\hline
&O\ \vdash& x: T0 <- e0: T1
\end{eqnarray*}
6 Un ejemplo más complicado
if e0 then e1 else e2 fi
Si \(e1\) tiene tipo \(T1\) y \(e2\) tiene tipo \(T2\), ¿qué tipo tiene que devolver esta expresión?
7 Mínimo común ancestro
El mínimo común ancestro (least common ancestor) de dos clases \(X,Y\) es la única clase \(Z\) que cumple \(X\le Z\) y \(Y\le Z\) y si otra clase \(W\) cumple \(X\le W\), \(Y\le W\) entonces \(Z\le W\).
8 Mínimo común ancestro
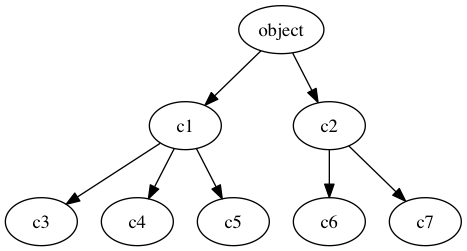
Figura 1: Árbol de clases
9 Tipos y evaluación de métodos
Cuando tenemos un método, ¿qué tipo tenemos que inferir?
\begin{eqnarray*}
&O\ \vdash& e0: T0\\
&O\ \vdash& e1: T1\\
&& \vdots\\
&O\ \vdash& en: Tn\\
\hline
&O\ \vdash& e0.f(e1,\ldots, en):?
\end{eqnarray*}
10 Notas sobre cool
- Métodos y objetos pueden tener el mismo identificado
- Hay dos ámbitos, uno para metodos y otro para objetos.
- Para los métodos, lo llamaremos \(M\) y para objetos \(O\)
- \(M(C,f)=(T_1,\ldots,T_{n+1})\) da información de los argumentos y el retorno
11 Reglas
\begin{eqnarray*}
&O,M\ \vdash& e0: T0\\
&O,M\ \vdash& e1: T1\\
&& \vdots\\
&O,M\ \vdash& en: Tn\\
M(T0,f) &= &(T1,\ldots, Tn,Tn+1)\\
\hline
&O\,M \vdash& e0.f(e1,\ldots, en):Tn+1
\end{eqnarray*}
12 Pregunta
Demostrar que, con el siguiente árbol:
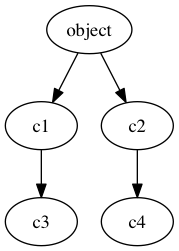
si \(O(x) = c3, O(y) = c1\) y \(M(f,c1)= (c1,c1)\), el tipo de \(x.f(y.f(x))\) es \(c1\).
13 Implementación de inferencia de tipos
\begin{eqnarray*}
&O,M,C\ \vdash& e0: INT\\
&O,M,C\ \vdash& e1: INT\\
\hline
&O\,M,C \vdash& e0+e1: INT
\end{eqnarray*}
Se traduce a código a:
typecheck(Environment,e1+e2){ T1 = typecheck(Environment, e1); T2 = typecheck(Environment, e1); Check T1 == T2 == Int; return Int; }
14 Implementación de inferencia de tipos
\begin{eqnarray*}
&O,M,C\ \vdash& e0: T0\\
&O(T/x),M,C\ \vdash& e1: T1\\
&&T0\le T\\
\hline
&O\,M,C \vdash& let\ x:T <- e0\ in\ e1: T1
\end{eqnarray*}
Se traduce a código a:
typecheck(Environment, let x:T <- e0 in e1 ){ T1 = typecheck(Environment, e0); T2 = typecheck(Environment.add(x:T), e1); Check(T0,T1); return T1; }