 Capítulo 2 :
Capítulo 2 :

 Estado del arte
Estado del arte



En muchas áreas del saber, el conocimiento se ha venido obteniendo por el clásico método hipotético-deductivo de la ciencia positiva. En él es fundamental el paso inductivo inicial: a partir de un conjunto de observaciones y de unos conocimientos previos, la intuición del investigador le conduce a formular la hipótesis. Esta "intuición" resulta inoperante cuando no se trata de observaciones aisladas y casuales, sino de millones de datos almacenados en soporte informático. En el fondo de todas las investigaciones sobre inducción en bases de datos subyace la idea de automatizar ese paso inductivo.
Las técnicas de análisis estadístico, desarrolladas hace tiempo, permiten obtener ciertas informaciones útiles, pero no inducir relaciones cualitativas generales, o leyes, previamente desconocidas; para esto se requieren técnicas de análisis inteligente ( [Frawley et al., 91] ) que todavía no han sido perfectamente establecidas. Por ello, se incrementa de forma continua la diferencia existente entre la cantidad de datos disponibles y el conocimiento extraído de los mismos. Pero cada vez más investigaciones dentro de la inteligencia artificial están enfocadas a la inducción de conocimiento en bases de datos. Consecuencia de esta creciente necesidad ha aparecido un nuevo campo de interés: la minería de datos (data mining), que incluye los nuevos métodos matemáticos y técnicas software para análisis inteligente de datos. La minería de datos surge a partir de sistemas de aprendizaje inductivo en ordenadores, al ser aplicados a bases de datos ( [Holsheimer y Siebes, 94] ), y su importancia crece de tal forma que incluso es posible que, en el futuro, los sistemas de aprendizaje se usen de forma masiva como herramientas para analizar datos a gran escala.
Se denomina descubrimiento de conocimiento en bases de datos (KDD) al proceso global de búsqueda de nuevo conocimiento a partir de los datos de una base de datos. Este proceso incluye no sólo el análisis inteligente de los datos con técnicas de minería de datos, sino también los pasos previos, como el filtrado y preprocesado de los datos, y los posteriores, como la interpretación y validación del conocimiento extraído.
Normalmente el término minería de datos lo usan estadísticos, analistas de datos, y la comunidad de sistemas de gestión de información, mientras que KDD es más utilizado en inteligencia artificial y aprendizaje en ordenadores.
El término descubrimiento de conocimiento en bases de datos (knowledge discovery in databases, o KDD para abreviar) empezó a utilizarse en 1989 1 para referirse al amplio proceso de búsqueda de conocimiento en bases de datos, y para enfatizar la aplicación a "alto nivel" de métodos específicos de minería de datos ( [Fayyad et al., 96b] ).
En general, el descubrimiento es un tipo de inducción de conocimiento, no supervisado ( [Michalski, 87] ), que implica dos procesos:
Entre la literatura dedicada al tema, se pueden encontrar varias definiciones para descubrimiento:
Los conceptos de lenguaje, certeza, simplicidad e interés, con los que se define el descubrimiento de conocimiento, son lo suficientemente vagos como para que esta definición cubra una amplia variedad de tendencias. Sin embargo, son ideas fundamentales que diferencian el KDD de otros sistemas de aprendizaje ( [Frawley et al., 91] ):
Cualquier algoritmo usado en un proceso de KDD debe considerar que conocimiento es una sentencia S expresada en un lenguaje L, cuyo interés I (según criterios del usuario) supera cierto umbral i (definido también por el usuario). A su vez, el interés depende de criterios de certeza, simplicidad y utilidad, establecidos por el usuario. Según se definan los umbrales para estos criterios, se puede enfatizar la búsqueda de información precisa (gran certeza), o útil, etc.
En [Brachman y Anand, 96] se define el proceso de KDD, desde un punto de vista práctico, como "una tarea intensiva en conocimiento que consta de complejas interacciones, prolongadas en el tiempo, entre un humano y una (gran) base de datos, posiblemente con la ayuda de un conjunto heterogéneo de herramientas".
Los principales pasos dentro del proceso interactivo e iterativo del KDD pueden verse en la figura 2-1 , y son los siguientes ( [Fayyad et al., 96b] y [Fayyad, 96] ):
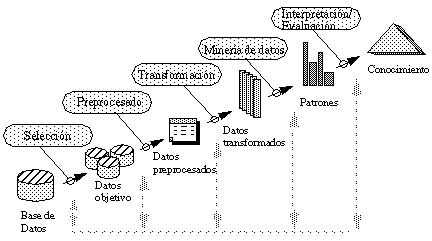
Muchas veces los pasos que constituyen el proceso de KDD no están tan claramente diferenciados como se muestra en la figura anterior. Las interacciones entre las decisiones tomadas en diferentes pasos, así como los parámetros de los métodos utilizados y la forma de representar el problema suelen ser extremadamente complejos. Pequeños cambios en una parte pueden afectar fuertemente al resto del proceso.
Sin quitar importancia a ninguno de estos pasos del proceso de KDD, se puede decir que la minería de los datos es la parte fundamental, en la que más esfuerzos se han realizado.
Históricamente, el desarrollo de la estadística nos ha proporcionado métodos para analizar datos y encontrar correlaciones y dependencias entre ellos. Sin embargo, el análisis de datos ha cambiado recientemente y ha adquirido una mayor importancia, debido principalmente a tres factores ( [Decker y Focardi, 95] ):
Estos nuevos métodos matemáticos y técnicas software, para análisis inteligente de datos y búsqueda de regularidades en los mismos, se denominan actualmente técnicas de minería de datos o data mining. A su vez, la minería de datos ha permitido el rápido desarrollo de lo que se conoce como descubrimiento de conocimiento en bases de datos.
Las técnicas de minería de datos han surgido a partir de sistemas de aprendizaje inductivo en ordenadores, siendo la principal diferencia entre ellos los datos sobre los que se realiza la búsqueda de nuevo conocimiento ( [Holsheimer y Siebes, 94] ). En el caso tradicional de aprendizaje en ordenadores (machine learning), se usa un conjunto de datos pequeño y cuidadosamente seleccionado para entrenar al sistema. Por el contrario, en la minería de datos se parte de una base de datos 2 , generalmente grande, en la que los datos han sido generados y almacenados para propósitos diferentes del aprendizaje con los mismos.
Podría parecer que una simple traducción de términos es suficiente para poder aplicar sobre las bases de datos técnicas tradicionales de aprendizaje en ordenadores ( tabla 2-1 ), realizando el aprendizaje sobre las tuplas de la base de datos en vez de sobre el conjunto de ejemplos. Sin embargo, la inducción de conocimiento en bases de datos se encuentra con dificultades no previstas por los tradicionales sistemas de aprendizaje, pues en el mundo real, las bases de datos suelen ser dinámicas, incompletas, ruidosas y muy grandes ( [Frawley et al., 91] ).
|
Base de datos = colección ficheros dinámicos, lógicamente integrados |
|
Por estos motivos, la mayoría de los algoritmos de aprendizaje son ineficientes al ser aplicados sobre bases de datos y gran parte del trabajo que se realiza en la inducción de conocimiento en bases de datos trata de solucionar estos problemas:
En la mayoría de las bases de datos, los datos son modificados de forma continua. Cuando el valor de los datos almacenados es función del tiempo, el conocimiento inducido varía según el instante en que se obtenga, y por ello es deseable un sistema que funcione de forma continua, en modo secuencial, para tener siempre actualizado el conocimiento extraído.
El manejo de datos incompletos en una base de datos puede deberse a pérdida de valores de algún atributo (al que se asigna entonces el valor desconocido), o a la ausencia del mismo en la vista que el sistema posee sobre los datos. En ambos casos, la incidencia en el resultado dependerá de si el dato incompleto es relevante o no para el objetivo del sistema de aprendizaje. Por ejemplo, un sistema para aprender a diagnosticar arritmias cardíacas no se verá afectado por la pérdida de datos como el color del pelo del paciente, pero sí por otros como el ritmo cardíaco.
El ruido existente en los datos viene determinado tanto por el tipo de valores de los atributos: real (ej. presión arterial), entero (ritmo cardíaco), cadena de caracteres (nombre del paciente) o nominal (tipo de arritmia), como por la exactitud en la medida de dichos valores (especialmente para atributos numéricos).
Por otro lado, es frecuente que las regularidades que se encuentran entre los datos de partida no se verifiquen siempre, sino con cierta probabilidad. Este efecto se debe no sólo a la presencia de ruido en la base de datos, sino también a la indeterminación existente en muchos aspectos de la realidad y a imprecisiones en el modelado de la misma (no hay que olvidar que en el diseño de la base de datos se modela la realidad, y todo modelo no es sino una aproximación más o menos precisa).
El tamaño de las bases de datos suele ser muy superior al de los conjuntos de entrenamiento de muchos sistemas de aprendizaje, por ello, en las bases de datos muy grandes es inabordable un análisis completo de todos los datos, y deben emplearse técnicas específicas que aceleren el aprendizaje sobre las mismas. Esto marca una importante diferencia entre los sistemas de inducción aplicables en uno y otro caso:
La viabilidad del aprendizaje en bases de datos ya ha empezado a ser reconocida por algunos gobiernos y empresas, como indica [Piatetsky-Shapiro, 91] , a pesar de que todavía es un tema que presenta algunas limitaciones. Por ejemplo, algunos bancos analizan bases de datos sobre créditos para encontrar los mejores criterios para su concesión o predecir situaciones de bancarrota. Otro ejemplo es la empresa General Motors, que construye de forma automática sistemas expertos para diagnosticar averías, partiendo para ello de bases de datos que recogen síntomas en los vehículos y problemas detectados. Cada vez se encuentran más referencias bibliográficas sobre aplicaciones prácticas de la minería de datos, como puede verse en [Decker y Focardi, 95] , [Shortland y Scarfe, 94] , [Mesrobian et al., 96] , [John et al., 96] , etc.
Por definición, se considera el KDD como un campo interdisciplinario en el que se reúnen investigadores de diferentes campos ( [Frawley et al., 91] , [Fayyad, 96] ). A continuación veremos cómo están relacionados cada uno de ellos con las distintas partes del proceso de KDD:
Aunque la estadística proporciona una valiosa ayuda en el análisis de datos, generalmente no es suficiente, y presenta algunos inconvenientes: mala adecuación a datos de tipo nominal, sus resultados pueden ser difíciles de interpretar, y requiere que el usuario decida dónde y cómo analizar los datos. Sin embargo, juega un importante papel en algunos pasos dentro del proceso de KDD, sobre todo en la selección y muestreo de datos, en la minería de datos y en la evaluación del conocimiento extraído.
Las técnicas de reconocimiento de patrones, especialmente las utilizadas para agrupamiento de conceptos (clustering) han contribuido en el proceso de KDD, sobre todo en la minería de datos. Estas técnicas utilizan estructuras de datos más sofisticadas que las técnicas estadísticas, a la vez que métodos más completos de búsqueda de conocimiento.
Las técnicas procedentes de la inteligencia artificial se centran casi exclusivamente en el manejo de datos de tipo simbólico, aportando algoritmos basados en la búsqueda heurística y en modelos no paramétricos.
Dentro de la inteligencia artificial, hay que destacar la importancia del aprendizaje en los ordenadores, sobre todo en la minería de datos, por sus técnicas para descubrir leyes, que describen relaciones cualitativas existentes en los datos. Otras áreas de la inteligencia artificial, como las relacionadas con el manejo de incertidumbre (por ej. redes bayesianas), representación del conocimiento o búsqueda, también tienen importancia en otros pasos dentro del KDD, como la transformación, selección y preprocesado de datos.
Un sistema gestor de datos es un programa que permite el almacenamiento, acceso y modificación de los datos almacenados en una base de datos. Mediante el lenguaje de manipulación de datos permite realizar de forma sencilla algunas operaciones, como la selección de tuplas que cumplen cierta condición, pudiendo dar lugar a inducir reglas interesantes, por ejemplo "el número de accidentes de tráfico ha crecido linealmente en los últimos 5 años". Sin embargo, es el usuario el que decide qué operaciones realizar en cada momento sobre los datos, y el que induce la regla ante la respuesta obtenida. Las bases de datos deductivas ( [Leung y Lee, 88] ) y orientadas a objetos proporcionan nuevas posibilidades de análisis inteligente de los datos e inducción de conocimiento ( [Silverschatz et al., 95] ).
Los almacenes de datos o warehouses son una de las nuevas áreas de interés dentro de las bases de datos. No son más que copias de los datos de una o varias bases de datos, con integración de esquemas, que proporcionan un acceso a los mismos de una forma sencilla y uniforme.
Pueden emplearse diferentes criterios para clasificar los sistemas de minería de datos y, en general, los sistemas de aprendizaje inductivo en ordenadores:
A continuación describiremos con más detalle los diferentes métodos de representación del conocimiento que se emplean en la minería de datos, dado que el lenguaje de representación es uno de los aspectos importantes para el proceso de KDD.
También veremos otro de los aspectos importantes para la minería de datos: el aprendizaje en los ordenadores, del que ha heredado las técnicas para extraer conocimiento a partir de los datos.
Los tradicionales sistemas de aprendizaje han utilizado con gran asiduidad, para representar el conocimiento, una extensión de la lógica de proposiciones, denominada lógica "0+" o representación objeto-atributo-valor. Dentro de la misma, pueden englobarse métodos de representación equivalentes como los árboles de decisión, las reglas de producción y las listas de decisión:
Los árboles de decisión son una forma de representación sencilla, muy usada entre los sistemas de aprendizaje supervisado, para clasificar ejemplos en un número finito de clases. Se basan en la partición del conjunto de ejemplos según ciertas condiciones que se aplican a los valores de los atributos. Su potencia descriptiva viene limitada por las condiciones o reglas con las que se divide el conjunto de entrenamiento; por ejemplo, estas reglas pueden ser simplemente relaciones de igualdad entre un atributo y un valor, o relaciones de comparación ("mayor que", etc.), etc.
Los sistemas basados en árboles de decisión forman una familia llamada TDIDT (Top-Down Induction of Decision Trees), cuyo representante más conocido es ID3 ( [Quinlan, 86] ).
ID3 (Interactive Dichotomizer) se basa en la reducción de la entropía media para seleccionar el atributo que genera cada partición (cada nodo del árbol), seleccionando aquél con el que la reducción es máxima. Los nodos del árbol están etiquetados con nombres de atributos, las ramas con los posibles valores del atributo, y las hojas con las diferentes clases. Existen versiones secuenciales de ID3, como ID5R ( [Utgoff, 89] ).
C4.5 ( [Quinlan, 93] , [Quinlan, 96] ) es una variante de ID3, que permite clasificar ejemplos con atributos que toman valores continuos.
Una desventaja de los árboles de decisión es que tienden a ser demasiado grandes en aplicaciones reales y, por tanto, se hacen difíciles de interpretar desde el punto de vista humano. Por ello, se han realizado diversos intentos para convertir los árboles de decisión en otras formas de representación, como las reglas de producción. Aquí consideramos reglas de producción del tipo si-entonces, basadas en lógica de proposiciones. El consecuente es una clase, y el antecedente es una expresión proposicional, que puede estar en forma normal conjuntiva (CNF) o ser simplemente un término.
En [Quinlan, 87] se propone una técnica para construir reglas de decisión, basadas en lógica de proposiciones, a partir de árboles de decisión. El problema es que incluso las reglas de producción así obtenidas pueden resultar demasiado complejas para un experto humano.
Algunos sistemas como PRISM, descrito en [Cendrowska, 88] , generan directamente reglas algo más sencillas, sin tener que construir el árbol previamente, mediante un algoritmo parecido a ID3 y con una precisión similar.
La familia AQ ( [Michalski, 87] ) la forman sistemas (AQ11, AQ15, etc.) que generan descripciones estructurales, por diferenciarlas de las descripciones de atributos de los sistemas anteriormente mencionados. Estas descripciones son también reglas de producción, aunque con mayor capacidad descriptiva, pues su antecedente es una fórmula lógica. La notación utilizada en estas reglas se denomina VL1 (Variable-valued Logic system 1, véase [Dietterich y Michalski, 84] ), y permite utilizar selectores (igualdad entre un atributo y un valor o conjunto de valores), complejos (conjunciones de selectores) y disyunciones de complejos para construir las reglas de producción.
Las listas de decisión son otra forma de representación basada en lógica de proposiciones. Es una generalización de los árboles de decisión y de representaciones conjuntivas (CNF) y disyuntivas (DNF). Una lista de decisión es una lista de pares de la forma
donde cada di es una descripción elemental, cada Ci es una clase, y la última descripción Cn es el valor verdadero. La clase de un objeto será Cj cuando dj sea la primera descripción que lo satisface. Por tanto, se puede pensar en una lista de decisión como en una regla de la forma "si d1 entonces C1, sino si d2..., sino si dn entonces Cn".
Se usan por ejemplo en el sistema CN2 ( [Clark y Niblett, 89] ) que es una modificación del sistema AQ, que pretende mejorar el aprendizaje a partir de ejemplos con ruido (al evitar la dependencia de ejemplos específicos e incorporar una poda del espacio de búsqueda). Las descripciones elementales de los pares que forman la lista de decisión tienen la misma forma que los complejos de AQ.
Aunque las representaciones basadas en lógica de proposiciones han sido usadas con éxito en muchos sistemas de aprendizaje en ordenadores, tienen algunas importantes limitaciones ( [Muggleton, 92] ), superadas por la lógica de predicados de primer orden, que restringen su campo de aplicación:
Todas estas limitaciones pueden superarse con una representación del conocimiento más potente: la lógica de predicados de primer orden. Cada vez hay más sistemas de aprendizaje en ordenadores que utilizan de algún modo la lógica de primer orden, surgiendo así un nuevo área de interés llamado programación lógica inductiva (en inglés Inductive Logic Programming o ILP). El objetivo de la programación lógica inductiva es construir un programa lógico (en lógica de predicados de primer orden) que, junto al conocimiento que se tenga del dominio, tenga como consecuencia lógica el conjunto de entrenamiento del sistema.
La presente tesis se enmarca dentro del paradigma de la programación lógica inductiva, por ello, en el apartado 2.4 , desarrollaremos este punto en mayor detalle, fijándonos en algunos de sus sistemas más representativos.
Las representaciones estructuradas de conocimiento tienen una gran potencia expresiva (aunque, en teoría, no mayor que la de la lógica de predicados de primer orden) y permiten una fácil interpretación del mismo. Entre las representaciones estructuradas se pueden incluir las redes semánticas y los marcos. En cualquier caso, el conocimiento expresado mediante una de estas representaciones estructuradas puede ser traducido fácilmente a lógica de predicados de primer orden.
El término de red semántica surge a partir del modelo de memoria semántica de Quillian (1968), con el que pretendía representar el significado de los vocablos del idioma inglés. En una red semántica la representación consta de un conjunto de nodos (conceptos), unidos entre sí por diferentes clases de enlaces asociativos (relaciones). A su vez, las relaciones entre un concepto y su clase, denominadas relaciones de subtipo (ej. instancia_de, es_un), a veces se representan en una red separada.
La principal ventaja de las redes semánticas es que toda la información relativa a un objeto concreto se obtiene fácilmente a partir del mismo, siguiendo los arcos que parten de él.
Para aplicar la minería de datos con redes semánticas, se representa cada ejemplo como una red semántica, y las operaciones que se realizan consisten en manipular los grafos, para encontrar los patrones (subgrafos) que cumplen todos los ejemplos de la misma clase.
Es práctica común el denominar red semántica a todo formalismo con forma de red usado para representar conocimiento. Sin embargo, es más preciso considerar como tales sólo las que se dedican a la representación del lenguaje natural, y denominar, en general, redes asociativas a todas ellas ( [Mira et al., 95] ).
Una red asociativa es una red (conjunto de nodos unidos entre sí por enlaces) en la que los nodos representan conceptos y los enlaces representan relaciones (de pertenencia, inclusión, causalidad, etc.) entre los conceptos. Dentro de las redes asociativas se incluyen: las redes semánticas (destinadas a representar o comprender el lenguaje natural), las redes de clasificación (representan conceptos mediante una jerarquía de clases y propiedades) y las redes causales (representan relaciones de influencia, generalmente de causalidad, entre variables).
Las redes de clasificación pueden considerarse redes semánticas sólo cuando representan conocimiento taxonómico de conceptos, pero no cuando se utilizan dentro de un sistema experto basado en marcos para definir clases e instancias.
Las redes causales representan un modelo en el que los nodos corresponden a variables y los enlaces a relaciones de influencia, generalmente de causalidad. Los modelos causales se orientan, sobre todo, a problemas de diagnóstico. Las redes bayesianas pueden considerarse como redes causales a las que se ha añadido una distribución de probabilidad sobre sus variables.
El concepto de marco fue introducido por Minsky (1975) como método de representación del conocimiento y de razonamiento, intentando superar las limitaciones de la lógica a la hora de abordar problemas como la visión artificial, la comprensión del lenguaje o el razonamiento de sentido común ( [Mira et al., 95] ).
Un marco es una estructura de datos, formada por un nombre y un conjunto de campos (o ranuras, del inglés slots), que se rellenan con valores para cada ejemplo concreto. Las ranuras pueden llenarse con valores de atributos o con referencias a otros marcos para expresar las relaciones de subtipo, como la relación es_un, en cuyo caso se heredan los atributos del marco de nivel superior.
Basándose en el concepto de marco, se desarrolló el lenguaje de programación KRL (Knowledge Representation Language), para representar el conocimiento de forma estructurada. La ingeniería del software también heredó de la inteligencia artificial el concepto de marco para construir la orientación a objetos (puede observarse el gran parecido entre los objetos de la programación orientada a objetos y los marcos).
Entre los sistemas de aprendizaje que utilizan marcos para representar el conocimiento adquirido, podemos mencionar el sistema EURISKO ( [Lenat., 84] ).
El conocimiento expresado mediante marcos puede traducirse fácilmente a lógica de predicados de primer orden, aunque perdiendo la ventaja de ser estructurado.
Los sistemas de aprendizaje basado en ejemplos (Instance-Based Learning algorithms) representan el conocimiento mediante ejemplos representativos, basándose en "similitudes" entre los datos ( [Aha et al., 91] ). El aprendizaje consiste en la selección de los ejemplos que mejor representan a los conceptos existentes en la base de datos (se trata de aprendizaje supervisado); estos ejemplos representativos serán los únicos que se almacenen, reduciendo así considerablemente el espacio necesario. El principal problema de estos sistemas es que se necesita una función de "similitud", a veces difícil de definir, para clasificar los nuevos ejemplos según sea su parecido con los ejemplos prototipo.
Los algoritmos de aprendizaje basado en ejemplos surgieron a partir de los clasificadores por vecindad (nearest-neighbor classifier), y han adquirido importancia más recientemente con los sistemas de razonamiento basado en casos (case-based reasoning), para diagnóstico y resolución de problemas. Además, pueden utilizarse como paso previo a otros sistemas de aprendizaje a partir de ejemplos, para entrenarlos con conjuntos de ejemplos más pequeños y representativos.
Las redes neuronales ( [Lippmann, 87] , [Freeman y Skapura, 93] , [Hertz et al., 91] ), incluidas dentro de los modelos conexionistas, son sistemas formados por un conjunto de sencillos elementos de computación llamados neuronas artificiales. Estas neuronas están interconectadas a través de unas conexiones con unos pesos asociados, que representan el conocimiento en la red. Cada neurona calcula la suma de sus entradas, ponderadas por los pesos de las conexiones, le resta un valor umbral y le aplica una función no lineal (por ej. una sigmoide); el resultado sirve de entrada a las neuronas de la capa siguiente (en redes como el perceptrón multicapa).
Uno de los algoritmos más usado para entrenar redes neuronales es el back-propagation, que utiliza un método iterativo para propagar los términos de error (diferencia entre valores obtenidos y valores deseados), necesarios para modificar los pesos de las conexiones interneuronales. El back-propagation puede considerarse como un método de regresión no lineal ( [Fayyad et al., 96b] ), en el que aplica un descenso de gradiente en el espacio de parámetros (pesos), para encontrar mínimos locales en la función de error.
Las redes neuronales han sido utilizadas con éxito en diferentes tipos de problemas:
Las tasas de error de las redes neuronales son equivalentes a las de las reglas generadas por los métodos de aprendizaje simbólicos, aunque son algo más robustas cuando los datos son ruidosos. Las principales desventajas para usar redes neuronales en la minería de datos son:
Entre la gran variedad de sistemas de aprendizaje desarrollados en ingeniería del conocimiento, se pueden distinguir dos claras tendencias desde un punto de vista psicológico: el enfoque conductista y el enfoque cognoscitivo. Esto marca diferentes actitudes de los sistemas ante el proceso de aprendizaje, así como su empleo en diferentes aplicaciones y el uso de diferentes lenguajes para representar el conocimiento.
Según la Psicología conductista, el aprendizaje es la capacidad de experimentar cambios adaptativos para mejorar el rendimiento. Siguiendo este enfoque, un sistema de aprendizaje será como una caja negra (de la que no interesa su estructura interna) capaz de adecuar su comportamiento para que el rendimiento de sus respuestas ante los datos de entrada aumente durante el proceso de aprendizaje.
Los sistemas de aprendizaje conductistas hacen mayor énfasis en modelos de comportamiento que en la representación interna del conocimiento, que muchas veces es opaca e ininteligible. Los lenguajes de descripción suelen ser diferentes para los objetos y para el conocimiento: los objetos se describen por vectores de características, mientras que para el conocimiento se emplean parámetros o tablas. En cualquier caso, esta representación del conocimiento hace difícil su traducción a reglas que expliquen de forma racional el comportamiento del sistema.
Las aplicaciones de los sistemas de aprendizaje conductista se extienden por varios campos relacionados con la IA: autómatas de aprendizaje, control adaptativo, reconocimiento de formas y clasificación. En general, presentan buena inmunidad al ruido.
Entre los sistemas conductistas de aprendizaje, hay que destacar los sistemas conexionistas y los sistemas evolucionistas, que realizan inducción de conocimiento.
Según el enfoque cognoscitivo de la Psicología, el aprendizaje consiste en la construcción y modificación de la representación del conocimiento. Durante el proceso de aprendizaje se produce un incremento del conocimiento, que no supone un simple cambio cuantitativo, sino también cualitativo; es decir, no hay un mero aumento del volumen de conocimiento almacenado, sino, sobre todo, una reorganización del mismo.
La "calidad" del aprendizaje vendrá dada no sólo por el aumento de precisión del conocimiento almacenado (en una base de conocimiento), sino también por la utilidad del mismo para los objetivos del usuario y por el nivel de abstracción empleado. Por tanto, la representación del conocimiento jugará un papel principal en los sistemas que sigan este enfoque.
Los lenguajes de descripción usados por estos sistemas suelen coincidir para representar a los objetos y al conocimiento. Están basados, normalmente, en la lógica (de proposiciones o de predicados) o en representaciones estructuradas (como los marcos).
Las aplicaciones de los sistemas de aprendizaje cognoscitivo dependen del tipo de aprendizaje que realicen, siendo los más importantes los que utilizan deducción (sistemas EBL, basados en explicaciones), analogía (sistemas expertos basados en casos) o inducción (adquisición y formación de conceptos). Los sistemas inductivos en los que el conocimiento se expresa mediante reglas sencillas se suelen denominar simbólico, y tienen gran importancia para construir bases de conocimiento en sistemas expertos y para extraer conocimiento de grandes bases de datos.
En cualquier proceso de aprendizaje, el aprendiz aplica el conocimiento poseído a la información que le llega, procedente de un maestro o del entorno, para obtener nuevo conocimiento, que es almacenado para poder ser usado posteriormente.
Dependiendo del esfuerzo requerido por el aprendiz (o número de inferencias que necesita sobre la información que tiene disponible) han sido identificadas varias estrategias, aunque, en la práctica, muchos procesos de aprendizaje aplican de forma simultánea varias de ellas. Una clasificación ya "clásica" de los diferentes tipos de aprendizaje, en orden creciente de esfuerzo inferencial por parte del aprendiz, es ( [Michalski, 87] ):
Se pueden diferenciar dos etapas en la evolución del conocimiento ( [Klir y Folger, 88] ): un esfuerzo orientado a conocer aspectos del mundo y un posterior esfuerzo por conocer aspectos del propio conocimiento. Se puede suponer que ésta segunda etapa, en la que nos encontramos hoy en día, surge a consecuencia de los fallos de la primera, para delimitar el alcance y validez del conocimiento adquirido previamente. Nuestra preocupación no se centra en la mera adquisición de conocimiento, sino que, además, se intenta determinar en qué medida conocemos algo, qué grado de certeza podemos asignar a nuestro conocimiento. Hemos desviado nuestros problemas desde cómo manipular el mundo a cómo manipular el conocimiento (y la ignorancia) en sí mismo.
Se ha calificado a la nuestra como la sociedad de la información, y se destinan gran cantidad de recursos a la adquisición, manejo, procesado, selección, almacenamiento, distribución, protección, recopilación, análisis y clasificación de la información, para lo cual el ordenador resulta una herramienta de gran ayuda.
La gran cantidad de información de que disponemos, unida al grado de incertidumbre que lleva asociada, constituye la base de muchos de los problemas actuales: la complejidad.
El estudio de la información basado en su incertidumbre asociada 11 ha dado lugar a diferentes teorías matemáticas. La primera de ellas fue la conocida teoría de la información de Shannon (1948), construida a partir de la teoría clásica de conjuntos y de la teoría de la probabilidad.
Desde comienzos de los 80 se han realizado diferentes avances orientados a la construcción de una teoría general de la información. Dentro de ésta se incluyen, además de la teoría clásica de conjuntos y de la teoría de la probabilidad, otras como la teoría de conjuntos borrosos, la teoría de la posibilidad y la teoría de la evidencia.
Con las nuevas teorías se ha conseguido romper la relación única que existía entre incertidumbre y teoría de la probabilidad, y se ha pasado a considerar la incertidumbre en los términos mucho más genéricos de la teoría de conjuntos borrosos y de medidas borrosas. Además, ha quedado demostrado que la incertidumbre puede manifestarse en diferentes formas o, dicho de otro modo, que existen diferentes tipos de incertidumbre y que en la teoría de la probabilidad sólo se manifestaba una de ellas.
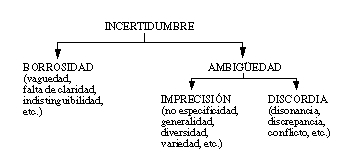
Los tres tipos de incertidumbre identificados con estas cinco teorías incluidas en la teoría general de la información son los siguientes:
La imprecisión y la discordia pueden considerarse como diferentes modos de ambigüedad, asociando esta última con cualquier situación en la que no quede clara la alternativa correcta de un conjunto de ellas. Ésta puede deberse a una defectuosa caracterización de un objeto (imprecisión) o a distinciones conflictivas (discordias). Por otro lado, la borrosidad es diferente de la ambigüedad, y se produce cuando existen conceptos cuyos límites no están perfectamente determinados.
Es posible que, en el futuro, se identifiquen otros tipos de incertidumbre, como resultado de la investigación de nuevas teorías sobre la incertidumbre.
Dentro de cada una de las teorías actualmente existentes es posible medir diferentes tipos de incertidumbre, como se muestra en la tabla 2-2 ( [Klir y Yuan, 95] ) para conjuntos finitos.
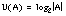 |
|||
 | |||
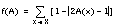 |
 |
||
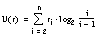 |
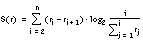 | ||
 |
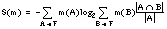 | ||
En el caso de conjuntos infinitos, no existen ecuaciones aplicables para algunas de las medidas de incertidumbre, en particular en las teorías de la probabilidad y de la evidencia. Otras, como la borrosidad en la teoría de los conjuntos borrosos, son fácilmente obtenidas a partir de la expresión para conjuntos finitos; en el caso de un conjunto infinito pero acotado en [a, b], este valor será:

El concepto de conjunto borroso fue introducido por [Zadeh, 65] , motivado por su interés por el análisis de sistemas complejos de control. En los conjuntos borrosos desaparece la drástica distinción entre miembros y no miembros de la teoría clásica de conjuntos, permitiendo que los elementos de un subconjunto A del conjunto universal U tengan asociado un grado de pertenencia comprendido en el intervalo [0, 1]. La función de pertenencia m sustituye a la función característica de los conjuntos clásicos:
Por este motivo, los conjuntos borrosos constituyen un método natural de representar la imprecisión y subjetividad propias de la actividad humana.
En el apartado A.1 pueden verse diferentes conceptos relacionados con los conjuntos borrosos, desde la definición del conjunto de pertenencia hasta la definición de diferentes operaciones aplicables sobre conjuntos borrosos, algunas de ellas también existentes para conjuntos clásicos (intersección, unión, complementación, etc.) y otras más específicas.
Del mismo modo que la teoría clásica de conjuntos y la lógica de proposiciones son isomorfas entre sí (ambas tienen estructura de álgebra de Boole), [Zadeh, 75] propone una lógica borrosa isomorfa con la teoría de conjuntos borrosos.
Conviene distinguir entre dos conceptos parecidos que pueden llevar a confusión: los conjuntos borrosos y las medidas borrosas.
Una medida borrosa representa incertidumbre en la pertenencia de un elemento a un conjunto, pero ésta no se debe a que el conjunto en sí mismo tenga naturaleza imprecisa o borrosa, sino a que no se conoce con precisión (aunque podría conocerse) en qué medida pertenece cada elemento a dicho conjunto. Las medidas borrosas se pueden realizar sobre conjuntos ordinarios (no borrosos). Por el contrario, los conjuntos borrosos tienen límites imprecisos, y por su propia definición no se puede determinar con precisión el grado de pertenencia de los elementos.
Sean tres conjuntos ordinarios, con las personas de edad menor que 20 años, entre 20 y 40 años, y mayor de 40 años. Estos conjuntos son ordinarios, pues no existe ninguna incertidumbre en sus límites. Sin embargo, para una persona concreta puede que no conozcamos su edad exacta sino sólo una estimación de la misma y, por tanto, no podamos clasificarla con total seguridad en ninguno de los conjuntos definidos. En ese caso, asignaremos un cierto grado de certeza o incertidumbre a su pertenencia a cada conjunto; esta representación de la incertidumbre se conoce como medida borrosa.
Por otro lado, también podríamos definir los conjuntos de las personas jóvenes y las viejas. En este caso, tendríamos conjuntos borrosos, pues los conceptos de joven y viejo no pueden separarse de forma rigurosa, sino que sus límites son difusos. Aunque conociéramos con precisión la edad de una persona, ésta tendría asociada un grado de pertenencia a cada uno de estos conjuntos borrosos.
Una medida borrosa se define ( [Klir y Yuan, 95] ) como una función de la forma
siendo C una familia no vacía de subconjuntos dentro de un conjunto universal U. La función g debe cumplir:
Puesto que para cualquier par de
conjuntos A y B se cumple que  y
y 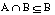 , aplicando la condición de monotonicidad se
comprueba que
, aplicando la condición de monotonicidad se
comprueba que
y, de modo análogo, se demuestra que
Dentro de la teoría de medidas borrosas se incluyen, entre otras, la teoría de la evidencia, la teoría de la posibilidad y la teoría de la probabilidad ( figura 2-5 ). La teoría de medidas borrosas (así como cualquiera de sus ramas) puede ser aplicada tanto sobre conjuntos ordinarios como sobre conjuntos borrosos.
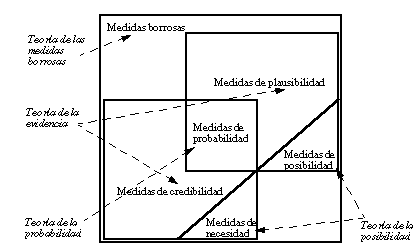
La teoría de la evidencia, de Dempster-Shafer, se basa en dos medidas duales no aditivas: medidas de credibilidad ( belief measures ) y medidas de plausibilidad ( plausibility measures ).
siendo P(U) el conjunto de subconjuntos de U (conjunto potencia). La función Bel debe cumplir:
Esta segunda expresión también se conoce como condición de superaditividad. Si U es infinito, entonces se requiere también que Bel sea continua desde arriba.
Para cualquier conjunto  , Bel(A) se interpreta como el grado de
credibilidad (basado en la evidencia disponible) de que un elemento dado de U
pertenezca al conjunto A.
, Bel(A) se interpreta como el grado de
credibilidad (basado en la evidencia disponible) de que un elemento dado de U
pertenezca al conjunto A.
Las medidas de plausibilidad y de credibilidad son duales entre sí. Se puede comprobar que
Para cualquier conjunto 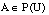 , Pl(A) se interpreta como el grado de
credibilidad (basado en la evidencia disponible) de que un elemento dado de U
pertenezca al conjunto A o a cualquier subconjunto cuya intersección con A sea
no vacía. Por tanto,
, Pl(A) se interpreta como el grado de
credibilidad (basado en la evidencia disponible) de que un elemento dado de U
pertenezca al conjunto A o a cualquier subconjunto cuya intersección con A sea
no vacía. Por tanto,
Las medidas de credibilidad y plausibilidad pueden ser caracterizadas por una función:
Esta función se denomina asignación de probabilidad básica. Dada una asignación básica m, los valores de credibilidad y plausibilidad se determinan de forma única:
Un caso particular de teoría de la evidencia es la teoría de la posibilidad. La teoría de la posibilidad maneja únicamente conjuntos anidados; dentro de ella caben mencionar las medidas de necesidad y de posibilidad, como casos particulares de las medidas de credibilidad y plausibilidad respectivamente.
Las medidas de necesidad (Nec) y posibilidad (Pos) cumplen:
que puede comprobarse que son casos particulares de las ecuaciones [EC. 2.32] y [EC. 2.33] .Cada medida de posibilidad Pos en el conjunto potencia P(U) se define de forma unívoca por una función distribución de posibilidad:
Otra forma alternativa de formular la teoría de la posibilidad es en términos de conjuntos borrosos. Las medidas de posibilidad están directamente conectadas con los conjuntos borrosos a través de las funciones de distribución de posibilidad:
Consideremos el conjunto borroso F, formado por los posibles valores de una variable V, y la expresión V = v, con el valor v F, para indicar que el valor de V es v. Entonces, para un valor concreto v, se puede interpretar mF(v) como el grado de compatibilidad de v con el concepto descrito por F; por otro lado, dada la proposición "V es F", es más sencillo interpretar mF(v) como el grado de posibilidad de la condición V = v. Es decir, para cada valor v se cumple que la posibilidad de V = v es numéricamente igual al grado de pertenencia de v al conjunto F:
Por tanto, la función distribución de posibilidad puede considerarse como una función de pertenencia normalizada (con al menos un grado de pertenencia igual a 1) 12 .
Una medida de probabilidad, Pro, debe satisfacer la condición de aditividad
que no es más que un caso particular (más restrictivo) de la condición de superaditividad. Las medidas de probabilidad son un tipo especial de medidas de credibilidad, como expresa el siguiente teorema: "una medida de credibilidad Bel en un conjunto potencia P(U) es una medida de probabilidad si y sólo si la función asignación de probabilidad básica m es tal que: m({x}) = Bel({x}) y m(A) = 0, para todo subconjunto A de U con más de un elemento".
Bajo estas condiciones, las medidas de credibilidad y plausibilidad coinciden:
No debe confundirse la probabilidad con el grado de pertenencia a un conjunto borroso (a diferencia de lo que ocurre con la posibilidad). Una forma rápida de comprobar que el grado de pertenencia de un elemento a un conjunto no se corresponde con su probabilidad de pertenecer a dicho conjunto, es viendo que los grados de pertenencia a los diferentes conjuntos borrosos no tienen por qué sumar uno y, sin embargo, la suma de las probabilidades de pertenecer a diferentes conjuntos debe ser igual a la unidad.
Por tanto, la teoría de la probabilidad, al igual que la teoría de la posibilidad, es un caso particular de la teoría de la evidencia, que a su vez está incluida en la teoría más general de las medidas borrosas ( figura 2-5 ).
El método que empleamos habitualmente para manejar con éxito la complejidad del mundo real consiste en simplificarla, buscando un compromiso entre la información de que disponemos y la incertidumbre que podemos permitir. Una opción es incrementar la cantidad de incertidumbre permitida, sacrificando parte de la información precisa en favor de una información más vaga pero más robusta.
Por ejemplo, en vez de describir el tiempo que hace hoy en términos de un porcentaje exacto de la porción de cielo cubierto por las nubes (que sería demasiado complejo), podemos decir simplemente que está soleado, lo cual reduce la complejidad añadiendo incertidumbre, aunque es una descripción mucho más útil. El lenguaje humano es típicamente impreciso o borroso y, sin embargo, no por ello carece de significación. El término "soleado" introduce cierto grado de imprecisión, dado que no lo usamos para indicar únicamente un 0% de nubes en el cielo, sino también un 10% de nubes, por ejemplo, o incluso un 20% de nubes. Por otro lado, sería inaceptable usarlo para un cielo cubierto de nubes en su totalidad, ni siquiera para un 80% de nubes. ¿Dónde establecemos entonces el límite entre un día soleado y un día cubierto?
Debemos aceptar que "soleado" introduce cierta imprecisión y que existe una separación vaga o borrosa (dependiente del porcentaje de cielo cubierto) entre los días soleados y los no soleados. Éste es precisamente el concepto de conjunto borroso o difuso (fuzzy set, [Zadeh, 65] ), que no es más que una generalización del tradicional conjunto ordinario ( crisp set ).
En [Fernández y Sáez-Vacas, 87] se defiende que la lógica borrosa va más allá que las lógicas multivaloradas con infinitos valores de verdad, porque no sólo considera que hay una infinidad de valores semánticos entre "verdadero" y "falso", sino que también tiene en cuenta que esos mismos valores de verdad son imprecisos. Así, por ejemplo, en lógica multivalorada se podría asignar el valor de verdad 0.7 a la sentencia "este párrafo es de difícil comprensión", pero no nos permitiría hacer inferencias imprecisas como "si alguien encuentra muy difícil comprender un párrafo, es probable que abandone su lectura". La lógica multivalorada no nos lo permite porque intervienen matices (relaciones entre "difícil", "muy difícil", "probable") imposibles de abordar con la simple extensión del conjunto de valores de verdad.
Ese tipo de inferencia imprecisa es el que pretende abordar la lógica borrosa, y para ello parte de la reconsideración del concepto matemático de conjunto . En la realidad pueden encontrarse infinidad de situaciones en las que resulta difícil determinar la pertenencia o no de un elemento a un conjunto:
Por tanto, en la lógica borrosa encontramos un método natural de representar la información del mundo real, gracias a la similitud existente entre los conceptos humanos y los conjuntos borrosos.
Podemos encontrar otros muchos ejemplos en los que el lenguaje humano introduce imprecisión, sin perder por ello significado. Es más, las relaciones imprecisas existentes entre el hombre y su entorno son mucho más significativas para el hombre que otro tipo de relaciones que podrían medirse con más precisión. Por ejemplo, cualquiera puede entender una orden imprecisa como "levanta ligera y lentamente el pie del embrague", mientras que es difícil realizar otras como "levanta el pie 10° a una velocidad de 2°30' por segundo".
De modo similar, en cualquier otro sistema complejo distinto del hombre, como las sociedades, una central térmica, etc. que se pretenda analizar, será imprescindible introducir en los modelos esta imprecisión y subjetividad utilizadas desde el punto de vista humano. Además, en este tipo de sistemas complejos, se cumple que significación y precisión son términos incompatibles ( [Zadeh, 73] ). Los resultados muy precisos suelen tener poco significado, y lo que interesa más bien son resultados cualitativos.
En la mayoría de los actuales sistemas expertos se presenta este problema: es necesario representar en la máquina los conocimientos y procedimientos inciertos e imprecisos que utilizan los expertos humanos para resolver problemas, y para ello se adoptan normalmente técnicas ad hoc . Pero existen intentos teóricos para introducir en la lógica formal la imprecisión y subjetividad característica de la actividad humana, y puede esperarse que en el futuro el diseño de sistemas expertos se base en tales teorías.
Parece claro que el conocimiento humano se basa en apreciaciones tanto de naturaleza probabilística (basada en la repetición de un fenómeno) como de tipo subjetivo o particular, que hacen necesario trabajar simultáneamente con probabilidades y con posibilidades para modelar de forma adecuada este conocimiento. Por ejemplo, en medicina es frecuente encontrar reglas probabilísticas como:
basadas en un estudio previo de pacientes a los que se ha suministrado dicha medicina. Sin embargo, reglas como:
están basadas en apreciaciones más o menos subjetivas sobre la atracción de las personas. Por tanto, es deseable utilizar un modelo en el que se puedan manipular conjuntamente ambos tipos de incertidumbre, como se propone en [Pons et al., 94] .
En un sistema experto borroso, el proceso de inferencia es una combinación de cuatro subprocesos ( [Horstkotte, 96] ):
En un plano de mayor abstracción cabe mencionar el trabajo de [González, 89] , en el que se propone una nueva arquitectura para la construcción de un entorno de desarrollo de sistemas expertos. Esta arquitectura está diseñada para ser utilizada en dominios en los que la incertidumbre es un factor esencial a considerar. Mediante esta arquitectura se pretende facilitar la aplicación de distintas metodologías de razonamiento aproximado, entre ellas la basada en conjuntos y lógica borrosa, el enfoque probabilista, etc.
El modelo relacional de base de datos, propuesto por Codd a principios de los años 70 ( [Codd, 70] ), es el predominante dentro de las bases de datos que existen en la actualidad. Quizá por ello, la mayoría de las bases de datos borrosas que se describen en la literatura se basan también en dicho modelo relacional.
En [Klir y Yuan, 95] se describe un modelo de base de datos borrosa (propuesto por Buckles y Petry en 1982), que incluye, como caso particular, al clásico modelo relacional. Las únicas diferencias incluidas en este nuevo modelo son dos:
La primera de estas diferencias permite, por ejemplo, representar diferentes opiniones de varios expertos, mediante un conjunto que las incluya a todas ellas dentro de una tupla. Por ejemplo, una relación que describa diferentes mercados para una empresa podría ser:
La segunda aportación de este modelo se basa en la suposición de que en el modelo relacional clásico existe una relación de equivalencia para cada dominio, de modo que se establecen clases de equivalencia (que coinciden con cada uno de los valores atómicos) en cada dominio. La generalización de esta idea conduce a la definición de relaciones de equivalencia borrosas (o relaciones de similitud) para cada dominio. Por ejemplo, para el dominio correspondiente al atributo "potencial" de la anterior relación, se pueden definir la siguiente relación de similitud, para los valores "excelente" (E), "bueno" (B), "regular" (R) y "malo" (M):
El álgebra relacional utilizada en este modelo de base de datos borrosa incluye las mismas operaciones que en el caso ordinario y, además, permite definir el mínimo grado de similitud aceptable entre elementos de cada dominio, para las operaciones de consulta a la base de datos.
Otra interesante extensión del modelo relacional para bases de datos borrosas se debe a Umano (1982). En este modelo, las relaciones que se utilizan son borrosas, ya que sus tuplas tienen un grado de pertenencia asociado.
También se introduce incertidumbre en las consultas a la base de datos, mediante la utilización de conjuntos borrosos para los dominios implicados en las mismas. De este modo, a partir de una relación ordinaria de la base de datos, se puede obtener una nueva relación borrosa añadiendo a cada tupla un grado de pertenencia dado por su similitud con el valor borroso utilizado en la consulta.
La selección de tuplas para una consulta dependerá del umbral de similitud que se defina.
En [Medina et al., 94] se propone una generalización que incluye los dos modelos anteriores de bases de datos relacionales borrosas. Para ello se utilizan nuevas estructuras de datos y un álgebra relacional modificada.
Los nuevos tipos de datos dentro de este modelo tienen como objetivo la representación de información borrosa, mediante distribuciones de posibilidad, números borrosos y etiquetas lingüísticas. Mediante estos nuevos tipos de datos se construyen las relaciones de la base de datos, denominadas "relaciones borrosas generalizadas".
Este modelo describe también un "Álgebra Relacional Borrosa Generalizada", con operaciones como la unión, intersección, diferencia producto cartesiano, proyección, join y selección, aplicables sobre las nuevas relaciones borrosas generalizadas.
En este modelo se pueden representar, por ejemplo, relaciones como la siguiente:
donde el símbolo & representa una distribución de posibilidad, y # significa "aproximadamente"; los valores "media", "buena", "normal" y "excelente" son etiquetas lingüísticas.
Y se pueden realizar consultas borrosas como: "dados el nombre, edad, productividad y salario, así como un grado de satisfacción mínimo para cada atributo, seleccionar las tuplas en las que se cumpla que la productividad es buena (en grado mayor que 0.9) y el salario es alto (en grado menor que 0.7)".
1. Según indica [Fayyad, 96] , la comunidad de KDD ha crecido de forma significativa en los últimos años, como muestra el creciente número de congresos organizados sobre este tema. La primera de estas reuniones (workshop) tuvo lugar en 1989, surgiendo a partir de ella el primer libro: [Piatetsky-Shapiro y Frawley, 91] . Hubo otras reuniones posteriores hasta la de 1994 (KDD-94 workshop) con 80 participantes, a partir de la cual se cambió el formato de las mismas para permitir la asistencia de público. En la última de ellas (Second International Conference on Knowledge Discovery and Data Mining o KDD-96) hubo unos 500 participantes.
2. En terminología de bases de datos, se conoce por base de datos al conjunto de datos lógicamente integrados, que pueden pertenecer a uno o más ficheros y residir en uno o varios nodos. En una base de datos relacional, los datos están organizados en tablas, con tuplas de tamaño fijo. El almacenamiento, actualización y recuperación de los datos la realiza el sistema gestor de la base de datos, usando información contenida en el diccionario de datos, como nombre de los atributos, dominios de los mismos, etc.
Por el contrario, en aprendizaje en ordenadores y, en general, en inteligencia artificial ( [Nilsson, 82] ) se entiende por base de datos una colección de ejemplos almacenados en un único fichero. Estos ejemplos son generalmente vectores de características de longitud fija. En ocasiones se dispone de información sobre los nombres de las características y sus rangos de valores, como si de un diccionario de datos se tratara.
3. Usaremos el término conocimiento de base (en inglés background knowledge) para designar todo lo que es conocido de antemano, para realizar el proceso de aprendizaje. Aunque, como señalan [Mira et al., 95] sería más acertado denominarlo información previa.
4. Parece que Michalski incluye aquí la implantación directa para completar la tabla pero, en general, nadie la considera un tipo de aprendizaje.
5. Estamos siguiendo aquí la interpretación dada por [Michalski, 84] , según la cual, cabe distinguir entre el conjunto de hechos u observaciones de partida y el conocimiento de base. El conocimiento de base está formado tanto por las suposiciones y restricciones en las observaciones de partida o en la forma del conocimiento que se puede inducir, como por cualquier conocimiento del problema que sea relevante. De acuerdo con este criterio, el conjunto de hechos lo forman las relaciones explícitas de la base de datos, mientras que las implícitas pertenecen al conocimiento de base.
Sin embargo, otros autores ( [Dzeroski, 96] ) consideran un conjunto de ejemplos, formado por hechos verdaderos y falsos de un predicado p, y un conocimiento de base, compuesto por el resto de predicados existentes (distintos de p) que pueden utilizarse para construir la definición de p. Según esta interpretación, el conocimiento de base vendría definido por todas las relaciones (intensionales y extensionales), con la excepción de la relación objetivo, que constituiría el conjunto de ejemplos.
6. La suposición de mundo cerrado o closed world assumption establece que todas las tuplas pertenecientes a P se declaran de forma explícita, por tanto, las no definidas se supondrán no pertenecientes a P. En FOIL es posible también declarar explícitamente las tuplas que no pertenecen a la relación P.
7. El significado intensional se refiere a la definición de un concepto, mientras que el extensional se refiere a los elementos a los que se les puede aplicar el concepto dentro de un universo determinado ( [Mira et al., 95] ). Por ejemplo, para "planetas solares":
- significado intensional: planetas que giran alrededor del Sol;
- significado extensional: {Mercurio, Venus, Tierra, Marte, Júpiter, Saturno, Urano, Neptuno, Plutón}
El significado intensional no varía (salvo que se redefina el concepto). Sin embargo el alcance extensional puede variar en el tiempo: el número de planetas puede aumentar o disminuir por un fenómeno cósmico o porque aumente nuestro conocimiento de la realidad.
9. Suponemos que el conjunto de entrenamiento local Ti es el que sirve para evaluar y seleccionar el literal i-ésimo Li de la cláusula en construcción. Las tuplas de Ti que satisfacen Li son seleccionadas para formar el nuevo conjunto Ti+1, tal como se describe en el apartado 2.5.3.2
10. Se define la precisión de una cláusula como la relación del número de tuplas positivas cubiertas respecto del total de tuplas cubiertas:
11. Existen diferentes enfoques para medir la información ( [Klir y Yuan, 95] ):
- Información como longitud de descripción: se basa en la teoría de la computación, y considera que la información representada por un objeto se puede medir por su longitud de descripción en algún lenguaje.
- Información basada en la incertidumbre: considera que la información y la incertidumbre son conceptos muy relacionados, pues ésta se produce como resultado de alguna deficiencia en la información. La información obtenida por una acción puede calcularse como la reducción de incertidumbre que produce, asumiendo que ésta se puede medir dentro de una teoría matemática concreta.
12. En el caso de que el conjunto F, del que se deriva el valor rF, no estuviera normalizado, no se podría aplicar la función de asignación de probabilidad básica, como se demuestra en [Klir y Yuan, 95] .