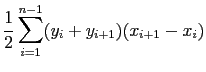Si tenemos unos valores 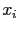$x_i$ en los que conocemos el valor de la función 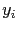$y_i$ , la fórmula que nos da la integral es:

$$\dfrac{1}{2}\sum_{i=1}^{n-1}(y_i + y_{i+1})(x_{i+1}-x_{i})$$

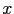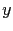Una forma práctica de plantear lo anterior en una hoja de cálculo es tener las $x$ y las $y$ , por ejemplo en columnas, y proceder de la siguiente forma:

1. crear otra columna donde se ponga la diferencia de cada 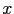$x$ con la superior (último factor de la fórmula); en la primera fila no se pone nada
2. crear otra columna donde se ponga la suma de cada 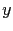$y$ con la superior (penúltimo factor de la fórmula); en la primera fila no se pone nada
3. crear otra columna donde se multiplican los dos valores de las columnas precedentes
4. sumar toda la columna y dividir por 2: ése es el resultado