Notes about Number Theory
(from book Number Theory with Programming, Authors: Marty Lewinter and Jeanine Meyer)
Triangular numbers
Triangular numbers are those that can be written as the sum of a consecutive
series of (whole) numbers beginning with 1. Thus 6 is triangular
because it is the sum of the first three numbers: 6 = 1 + 2 + 3. The first
few triangular numbers are 1, 3, 6, 10, 15, 21, 28, 36, 45, and 55. We
denote the nth triangular number by tn. Thus t5 = 1 + 2 + 3 + 4 + 5 =15.
More generally,
tn =1+2+3+ ... + (n−2) + (n−1) + n
The nth triangular number is given by the formula:
tn =1+2+3+ ... + n = n(n+1)/2
It should be noted that
tn − tn − 1 = n
The sum of any two consecutive triangular numbers is a square:
tn + tn − 1 = n2
Oblong numbers and Squares
A positive integer of the form n(n + 1) is called oblong. The nth oblong
number is the sum of the first n even numbers. To see this, observe that
the nth even number is 2n. Then we have 2 + 4 + 6 + ... + 2n =
2 (1+2+ ... + n) = 2(n (n+1)/2)= n (n+1) , the nth oblong number.
The sum of the first n odd numbers: The nth odd number is 2n − 1.
So 1+3+5+ ... + (2n−1) = (2×1−1) + (2×2−1) + (2×3−1) + ... + 2n−1 , in which -1 appears n times.
We then get
2 (1+2+3+ ... + n) - n = 2(n (n+1)/2) - n = n (n+1) - n = n2 + n - n = n2
So the sum of the first n odd numbers is n2
Deficient, Abundant, Perfect numbers
The Pythagoreans classified all numbers as deficient, abundant, or perfect. Given a number, find all of its proper factors, that is, all numbers that go into it (with the exclusion of the given number). The proper factors of 30, for example, are 1, 2, 3, 5, 6, 10, and 15.
If the sum of the proper factors of n is less than n, we call n deficient. If the sum exceeds n, it is called abundant. If the sum equals n, we call it perfect. For example, 8 is deficient since 1 + 2 + 4 < 8, 18 is abundant since 1 + 2 + 3 + 6 + 9 > 18, and 28 is perfect since 1 + 2 + 4 + 7 + 14 = 28. The smallest perfect number is 6. The first few perfect numbers are 6, 28, 496, and 8128.
Primes, Fibonacci sequence and the Pell equation
A prime number is a number that has no divisors other than itself or 1.
A number that has divisors (or factors) other than itself and 1 is called composite.
A composite number must have a prime divisor.
In the sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,…, each term is the
sum of the preceding two terms. We denote these Fibonacci numbers by
u1, u2, u3, …. Thus, un is the nth Fibonacci number. Now, u1 = 1 and
u2 = 1 are the seed since they determine the rest of the terms.
The relationship between the general term and the two preceding terms is called the recursive relation and is
written as
un + 2 = un + un + 1
The sequence of ratios of the form
un + 1/ un, that is, the ratios consisting
of each term divided by its predecessor approach a limit. The limit is the famous irrational
number, denoted by the Greek letter Φ, known as the golden ratio (its approximate value is 1.618).
An equation of the form
x2 − ky2 = ±1
where k ≥ 2, is called a Pell equation.
Goldbach's conjecture:
Goldbach conjectured that every even number
greater than 4 is the sum of two odd primes.
Factorials
n! or n factorial, is the product of the first n
positive integers, that is,
n! = n × n−1 × n−2 × ... × 3 × 2 × 1
\[
n! = \prod_{i=1}^{n}i
\]
We define 0! to be 1. There are n! permutations of n distinct objects.
Using recursion, factorial is
\begin{align}
0! = 1 \\
n! = n \cdot (n-1)! \hspace{1em} when \hspace{1em} n \geq 1
\end{align}
The combinatorial numbers n choose k
Given n distinct objects, in
how many ways can we select k of them where order does not matter?
We can deduce the following expression
\begin{align}
\binom{n}{k} = \frac{n!}{k!\left ( n-k \right )!} \\
equivalence: \hspace{1em} \binom{n}{n-k} = \binom{n}{k} \\
\end{align}
Pascal's Triangle
Each entry is the sum of the two entries immediately above it.
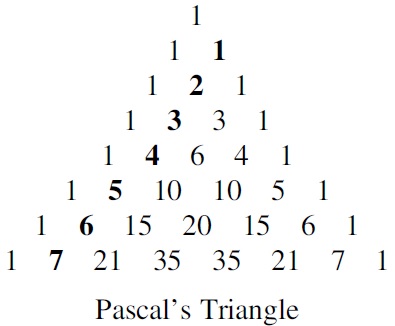
The Pascal's Triangle has many interesting properties.
Binomial coefficients
the entries of the nth row of Pascal’s triangle
consist of the n + 1 combinatorial numbers:
\begin{align}
\binom{n}{0},\,\binom{n}{1}, \,\binom{n}{2}, ... , \binom{n}{n-2}, \,\binom{n}{n-1},\,\binom{n}{n}
\end{align}
These combinatorial numbers are the coefficients in the expansion
of (a + b)n and are often called binomial coefficients.
Catalan numbers
The Catalan numbers are defined by \[ c_{n} = \frac{1}{n+1}\binom{2n}{n} \] and are useful in combinatorics, number theory, and computer science. They satisfy the recurrence relation \[c_{n} = \frac{2(2n-1)}{n+1}c_{n-1}\] Find the first 100 Catalan numbers (i) using this recurrence and (ii) using the definition. Which is faster?
Divisors and Prime decomposition
Divisors
A factor of a number is called a divisor. Thus, 10 has the divisors 1, 2, 5, and 10. The divisors of n other than n are called proper divisors. The proper divisors of 10 are, therefore, 1, 2, and 5, while its divisors are 1, 2, 5, and 10. A divisor of n is said to divide n. Thus, 5 divides 10, while 7 does not divide 10. The symbol for “divides” is a vertical line. When a divides b, we write a | b. Whenever a divides b, observe that b is a multiple of a, that is, b = ka, for some integer k. Thus, 5 | 10, while 10 = 2 × 5. In fact, this is an “if and only if” statement: a divides b if and only if b is a multiple of a.
Here are a few laws of divisibility. All letters represent integers (whole numbers) unless otherwise stated:
- a | b and b | c \( \Rightarrow \) a | c.
- a | b and b | a \( \Leftrightarrow \) a = ±b.
- a | b and c | d \( \Rightarrow \) ac | bd.
- a | b \( \Rightarrow \) ac | bc (where c \( \neq \) 0).
- a | r and a | s \( \Rightarrow \) a | (mr + ns).
- a | r and a does not divide s \( \Rightarrow \) a does not divide r + s.
- If a and b are positive integers such that a | b, then a \( \leqslant \) b.
Greatest Common Divisor (GCD)
Given a and b, we call d the greatest common divisor of a and b, denoted gcd(a,b), if:
- d | a and d | b.
- d is the greatest number that divides both a and b.
If gcd(a,b) = 1, we say that a and b are relatively prime, that is, they have no common divisor other than 1.
Division: Given integers a and b, where a is positive, there exists a pair of numbers, q (for quotient) and r (for remainder), where 0 \( \leq \)r < a, such that b = qa + r.
So we can state gcd(a,b) = gcd(a, b − qa)
Euclid's algorithm pseudocode for finding the gcd of two numbers:
Division-based version
function gcd(a, b)
while b ≠ 0
t = b
b = a mod b
a = t
return a
Subtraction-based version
function gcd(a, b)
while a ≠ b
if a > b
a = a − b
else
b = b − a
return a
Recursive version
function gcd(a, b)
if b = 0
return a
else
return gcd(b, a mod b)
Least Common Multiple (LCM)
Given integers a and b, the smallest positive integer, c, such that a | c and b | c is called their least common multiple and is denoted lcm (a,b).
Relation LCM and GCD: \[ lcm(a,b) = \frac{a \times b}{gcd(a,b)} \]
Modular arithmetic
Modular arithmetic sheds light on the relation of integers to their remainders when they are divided by a given positive integer.
Modular equation
ax = b (mod n), where a, b, and n are given, is a modular equation
Number theoretic functions
The tau function
The function \(\tau (n)\) counts how many divisors \(n\) has. This count includes 1 and \(n\).
The Sigma function
The sum of the divisors of \(n\) is denoted \(\sigma (n)\).
The first few values of \(\sigma (n)\) are given by \(\sigma (1)\) = 1, \(\sigma (2)\) = 1 + 2 = 3, \(\sigma (3)\) = 1 + 3 = 4, \(\sigma (5)\) = 1 + 5 = 6, \(\sigma (6)\) = 1 + 2 + 3 + 6 = 12, \(\sigma (7)\) = 1 + 7 = 8, and \(\sigma (9)\) = 1 + 3 + 9 = 13.
Multiplicative function
A multiplicative function, f, satisfies:
1. f(1) = 1.
2. f(mn) = f(m)f(n) whenever gcd(m,n) = 1.
\(\tau (n)\) and \(\sigma (n)\) are examples of multiplicative functions.
Perfect numbers revisited
Recall that a perfect number is the sum of its proper divisors. It follows that \(n\) is perfect if and only if \(\sigma (n) = 2n\), since \(\sigma\) counts \(n\) as a divisor.
For example, the perfect number 6 satisfies \(\sigma (6) = 1 + 2 + 3 + 6 = 12 = 2 × 6\)
The Riemann Zeta Function
The Riemann zeta function is defined by
\[ \zeta (s) = \sum_{n=1}^{\infty }\frac{1}{n^{s}}=1 +\frac{1}{2^{s}}+\frac{1}{3^{s}}+\frac{1}{4^{s}}+\cdots \]where \(s \) is a complex number with certain restrictions. If we restrict \(s \) to positive integer values, for example when s = 1, we obtain a divergent series. The eighteenth-century mathematician Euler showed, using calculus, that \( \zeta (2) = \frac{\pi^{2}}{6} \)
The Phi Function
The number of positive integers less than \(n\) that are relatively prime to \(n\) is denoted \( \phi (n) \). The first few values of this important function, called the Euler \( \phi \) function, are given by \( \phi (1)=1 \), \( \phi (2)=1 \), \( \phi (3)=2 \), \( \phi (4)=2 \), \( \phi (5)=4 \), \( \phi (6)=2 \) (since only 1 and 5 are relatively prime to 6), \( \phi (7)=6 \), \( \phi (8)=4 \), \( \phi (9)=6 \), and \( \phi (10)=4 \).
Computing the Euler phi function from the definition can be done using a gcd function.
Factoring large number - Fermat method
Fermat developed the following method of factoring large numbers:
If we wish to factor a large even number, \(n\), we observe that 2 is a factor and therefore divide by 2 and consider \( \frac{n}{2} \). If \( \frac{n}{2} \) is even, divide it by 2, note that \(4 = 2^{2} \) is a factor of \(n\), and consider \( \frac{n}{4} \). After k divisions by 2, we will reach an odd number, \(m\), and realize that \(n = 2^{k}m \). If m = 1, we are done. Otherwise, the problem of factoring \(n\) boils down to factoring the odd number \(m\). So Fermat dealt exclusively with the problem of factoring a large odd number.
If \(m = a^{2} - b^{2}\), where \(a - b \gt 1\), we have the nontrivial factorization \(m = (a + b)(a − b)\). Fermat developed a way to express m as the difference of two squares. That is, he tried to find \(a\) and \(b\) such that the given odd number \(m = a^{2} - b^{2}\) or \(a^{2} - m = b^{2}\). To do this, he found the smallest \(N\) for which \(N^{2} \gt m\). Then he considered the sequence \(N^{2} - m\), \((N + 1)^{2} - m\), \((N + 2)^{2} - m\),…, until he found a square. This enabled him to write \(m = a^{2} - b^{2} = (a + b)(a − b)\).
Example: Factor 119 using Fermat’s method. The smallest N for which \(N^{2} \gt 119\) is 11. Now, 112 − 119 = 121 − 119 = 2, which is not a square. We then examine 122 − 119 = 144 − 119 = 25, which is a square. Then 119 = 144 − 25 = (12 − 5)(12 + 5) = 7 × 17.
Programs of Number Theory
Computing specific triangular number using sum and measuring time
import time
start = time.time()
n = 1000000
sum = 0
for i in range(1,n+1):
sum+=i
print("The "+ str(n)+" th triangular number is "+ str(sum))
end = time.time()
elapsed = end-start
print("Elapsed time was "+ str(elapsed))
Listing the proper factors of a number
# Listing the proper factors of a number (30)
def countUpFactors(n):
count = 0
print("Proper factors of "+ str(n) + " are: ")
for i in range(1,n):
if ((n%i)==0):
count+=1
print(i)
print("The number of proper factors of "+ str(n)+" is "+ str(count))
n = 30;
countUpFactors(n)
Characterizing a number as deficient, perfect, or abundant, for specific small set of number
# Characterizing a number as deficient, perfect, or abundant, for specific small set of number ( 6, 8, 18, 28, 945, 8128)
#
#n = int(input('Numero?: '))
n =[6,8,18,28,945,8128]
for num in n:
i = 1
suma = 0
print('Proper factors of ',num, ' are: ' )
while i < num:
if (num % i == 0):
print (i)
suma += i
i += 1
print('The sum of the proper factors of ',num,' is ',suma, end = '')
if (suma == num):
print(', so ', num,' is perfect')
elif (suma < num):
print(', so ', num,' is deficient')
else:
print(', so ', num,' is abundant')
Checking conjecture on no odd number being perfect for first 1000 odd numbers
# Checking conjecture on no odd number being perfect for first 1000 odd numbers
def classify(n):
sum = 0
for i in range (1,n):
if ((n%i)==0):
sum += i
if (sum
Simple program generating primes up to 10000
# Simple program generating primes up to m
import math
def primes(m):
for n in range(2,m+1):
#check if n is a prime
#first obtain its square root. We make use of a built-in function in math
s=int(math.sqrt(n));
#we have proved n is NOT a prime if we find a factor.
#we set up what is termed a flag variable. It starts out being true.
noFactorSoFar = True;
for f in range (2,s+1):
#is f a factor of n? We make use of the modulo operator, %.
#It essentially produces the remainder
r = n % f
#r being zero means no remainder, n was divisible by f
if (r==0):
noFactorSoFar = False
break # leave the inner f loop because we found a factor
# continue with f loop
# ends the f loop
if (noFactorSoFar):
#never found a factor
print(n, end=", ")
primes(10000)
Listing primes, counting steps
# Improved listing of primes: just using primes, counting steps
import math
def fprimes(m):
primes=[2] # we treat 2 as a prime
count = 0
np = 0
for n in range(3,m):
#check if n is a prime
#first obtain its square root. We make use of a built-in function in JavaScript
s=int(math.sqrt(n));
#we have proved n is NOT a prime if we find a factor.
#we set up what is termed a flag variable. It starts out being true.
noFactorSoFar = True
# instead of checking all the numbers, we just check the primes
# the && does a logical AND test BUT it will only calculate the second term
# if the first is true. This is sometimes called "lazy".
fi = 0
while fi < len(primes) and primes[fi]<=s :
#is f a factor of n? We make use of the modulo operator, %.
#It essentially produces the remainder
f=primes[fi]
r = n % f
count+=1
#r being zero means no remainder, n was divisible by f
if (r==0):
noFactorSoFar = False
break # leave the inner f loop because we found a factor
# continue with f loop
# ends the f loop
fi += 1
for f in range (2,s+1):
#is f a factor of n? We make use of the modulo operator, %.
#It essentially produces the remainder
r = n % f
#r being zero means no remainder, n was divisible by f
if (r==0):
noFactorSoFar = False
break # leave the inner f loop because we found a factor
# continue with f loop
# ends the f loop
if (noFactorSoFar):
#never found a factor
print(n, end=", ")
primes.append(n) #add n to our list (array) of primes
np+=1
print("Number of % operations performed: ", count, end="\n")
print("Number of primes (starting with 3): ", np)
fprimes(1000)
Solve a Pell equation using crude check on x, y values
# Solve a Pell equation using crude check on x, y values
import math
print("Solutions of x**2 - 3*y**2 = 1")
print("------------------------------")
# k is 3
k=3
# start with n set to 1. This will produce the x=a and y=b values (3,1)
for x in range(1, 1000+1):
h = (x*x-1)/k
yy = math.sqrt(h)
y = math.floor(yy + .5)
#idea is that the rounded off integer value won't work
if ((x*x-3*y*y)==1):
print("x = ", str(x), ", y = ",str(y))
Find pairs of primes adding to given even number
# Find pairs of primes adding to given even number
import math
def fprimes(m):
global primes
primes=[2] # we treat 2 as a prime
for n in range(3,m):
#check if n is a prime
#first obtain its square root. We make use of a built-in function in JavaScript
s=int(math.sqrt(n));
#we have proved n is NOT a prime if we find a factor.
#we set up what is termed a flag variable. It starts out being true.
noFactorSoFar = True
# instead of checking all the numbers, we just check the primes
# the && does a logical AND test BUT it will only calculate the second term
# if the first is true. This is sometimes called "lazy".
fi = 0
while fi < len(primes) and primes[fi]<=s :
#is f a factor of n? We make use of the modulo operator, %.
#It essentially produces the remainder
f=primes[fi]
r = n % f
#r being zero means no remainder, n was divisible by f
if (r==0):
noFactorSoFar = False
break # leave the inner f loop because we found a factor
# continue with f loop
# ends the f loop
fi += 1
if (noFactorSoFar):
#never found a factor
primes.append(n) #add n to our list (array) of primes
def isPrime(c) :
global primes
return (c in primes)
def findpairs(number):
global primes
answer = "" #will use to construct the answer
count = 0
if ((number%2)>0):
print("Your number must be even. Try again")
return False
if (number > limit) :
print("Your number is greater than ",limit,". Please try a smaller number.")
return False
h = int(number / 2)
for f in range(1,h+1):
#need to check if f and (number-f) both primes. Use lazy evaluation
if (isPrime(f) and isPrime(number-f)) :
answer += str(f)+ " and "+ str(number-f)+" \n"
count+=1
if (len(answer)>0) : #were any pairs found?
answer += str(count)+" pairs of primes adding up to " + str(number)
else:
answer = "No pairs of primes adding up to " + str(number)
print(answer)
return False # required to prevent the broswer from re-loading original document
limit = 10000
n = int(input('Numero?: '))
fprimes(n)
findpairs(n)
Factorial using iteration
# Factorial using iteration
import time
n = int(input('Numero?: '))
start = time.time()
ans = 1
for j in range(1,n+1):
ans *= j
end = time.time()
elapsed = end-start
print("Factorial(", n,") = ", ans, " Elapsed time was "+ str(elapsed) )
Factorial using recursion
# Factorial using recursion
import time
def factr(n):
if (n<=1):
return 1
else :
return n*factr(n-1)
n = int(input('Numero?: '))
start = time.time()
ans = factr(n)
end = time.time()
elapsed = end-start
print("Factorial(", n,") = ", ans, " Elapsed time was "+ str(elapsed) )
Pascal's triangle
#Pascal's triangle
def triangle(limit):
output =" 1 \n"
last = [1]
val = []
limit -= 1
while (limit>=0):
#add at 0 and append each change the array itself. Each returns new length
last.insert(0,0)
count = len(last)
last.append(0)
next = []
for i in range(count):
val = last[i]+last[i+1]
next.append(val)
output = output + " " + str(val)
output += "\n"
last = next
limit -= 1
print(output)
n = int(input('Numero?: '))
triangle(n)
Greatest Common Divisor
#gcd
def gcd(a,b):
if (b < a):
a,b = b,a
r = b % a
if (r==0):
return a
else:
return gcd(r,a)
a,b = [int(x) for x in input("Enter two integer value: ").split()]
print("GCD is ", gcd(a,b))
Prime decomposition of a number
# Prime decomposition of a number
import math
table = [] #each element will be an array of length 2
def produceFactors(n):
ans = [] #start off with empty array
#notice start with 2, not 1
for i in range(2, n+1):
if ((n%i)==0):
ans.append(i)
return ans
def onlyprimes(factors):
ans = []
for i in range(len(factors)):
if (isPrime(factors[i])):
ans.append(factors[i])
return ans
def makeTable(m,facs):
global table
while (len(facs)>0):
f = facs[0] #always using first, that is, 0th element
if ((m % f)>0):
#f, the ith element of facs does NOT divide m
facs.pop(0) #remove this factor
else:
m = m / f
e=1
#need to see if exponent is more than 1
while (0 == (m%f) ):
m = m /f
e+=1
table.append([f,e])
facs.pop(0)
return
def isPrime(n):
lim = int(math.sqrt(n))
for i in range (2, lim+1):
if (0 == n % i):
return False
return True
def displaydecomp(n):
global table
table = [] #reset table to empty array
factors = produceFactors(n)
pfactors = onlyprimes(factors)
makeTable(n, pfactors) # this function will add to table
messages = "The prime decomposition is \n"
for i in range(len(table)):
messages += str(table[i][0])+"**"+str(table[i][1])+" "
print(messages)
n = int(input('Numero?: '))
displaydecomp(n)
Display list of proper factors
# Display list of proper factors
def produceFactors(n):
ans = [] #start off with empty array
for i in range(1,n):
if ((n%i)==0):
ans.append(i)
return ans;
def getfactors(n):
messages = "The proper factors are \n"
factors = produceFactors(n)
for i in range (len(factors)):
messages += str(factors[i])+"\n"
print(messages)
n = int(input('Numero?: '))
getfactors(n)
Tau from definition
# Tau from definition
def produceFactors(n):
ans = [] #start off with empty array
for i in range(1,n):
if ((n%i)==0):
ans.append(i)
return ans;
def tau(n):
t = len(produceFactors(n))+1
messages = "The value of tau for "+ str(n)+" is "+ str(t)
print(messages)
n = int(input('Numero?: '))
tau(n)
Counting letters
# Counting letters
# console:
# >python cuentacar.py < texto.txt
def countLetters(txt):
counts= {}
for i in range(len(txt)):
if (txt[i].isalnum()):
if (counts.get(txt[i])==None):
counts.update({txt[i]: 1})
else :
count= counts.get(txt[i])
count += 1
counts.update({txt[i]: count})
for key, value in counts.items():
print(key, ' : ', value)
txt = input('Enter text: ').lower()
countLetters(txt)