## module jacobi
''' lam,x = jacobi(a,tol = 1.0e-8).
Solution of std. eigenvalue problem [a]{x} = lam{x}
by Jacobi's method. Returns eigenvalues in vector {lam}
and the eigenvectors as columns of matrix [x].
'''
import numpy as np
import math
def jacobi(a,tol = 1.0e-8): # Jacobi method
def threshold(a):
sum = 0.0
for i in range(n-1):
for j in range (i+1,n):
sum = sum + abs(a[i,j])
return 0.5*sum/n/(n-1)
def rotate(a,p,k,l): # Rotate to make a[k,l] = 0
aDiff = a[l,l] - a[k,k]
if abs(a[k,l]) < abs(aDiff)*1.0e-36: t = a[k,l]/aDiff
else:
phi = aDiff/(2.0*a[k,l])
t = 1.0/(abs(phi) + math.sqrt(phi**2 + 1.0))
if phi < 0.0: t = -t
c = 1.0/math.sqrt(t**2 + 1.0); s = t*c
tau = s/(1.0 + c)
temp = a[k,l]
a[k,l] = 0.0
a[k,k] = a[k,k] - t*temp
a[l,l] = a[l,l] + t*temp
for i in range(k): # Case of i < k
temp = a[i,k]
a[i,k] = temp - s*(a[i,l] + tau*temp)
a[i,l] = a[i,l] + s*(temp - tau*a[i,l])
for i in range(k+1,l): # Case of k < i < l
temp = a[k,i]
a[k,i] = temp - s*(a[i,l] + tau*a[k,i])
a[i,l] = a[i,l] + s*(temp - tau*a[i,l])
for i in range(l+1,n): # Case of i > l
temp = a[k,i]
a[k,i] = temp - s*(a[l,i] + tau*temp)
a[l,i] = a[l,i] + s*(temp - tau*a[l,i])
for i in range(n): # Update transformation matrix
temp = p[i,k]
p[i,k] = temp - s*(p[i,l] + tau*p[i,k])
p[i,l] = p[i,l] + s*(temp - tau*p[i,l])
n = len(a)
p = np.identity(n,float)
for k in range(20):
mu = threshold(a) # Compute new threshold
for i in range(n-1): # Sweep through matrix
for j in range(i+1,n):
if abs(a[i,j]) >= mu:
rotate(a,p,i,j)
if mu <= tol: return np.diagonal(a),p
print('Jacobi method did not converge')
## module sortJacobi
''' sortJacobi(lam,x).
Sorts the eigenvalues {lam} and eigenvectors [x]
in order of ascending eigenvalues.
'''
import swap
def sortJacobi(lam,x):
n = len(lam)
for i in range(n-1):
index = i
val = lam[i]
for j in range(i+1,n):
if lam[j] < val:
index = j
val = lam[j]
if index != i:
swap.swapRows(lam,i,index)
swap.swapCols(x,i,index)
## module stdForm
''' h,t = stdForm(a,b).
Transforms the eigenvalue problem [a]{x} = lam[b]{x}
to the standard form [h]{z} = lam{z}. The eigenvectors
are related by {x} = [t]{z}.
'''
import numpy as np
from choleski import *
def stdForm(a,b):
def invert(L): # Inverts lower triangular matrix L
n = len(L)
for j in range(n-1):
L[j,j] = 1.0/L[j,j]
for i in range(j+1,n):
L[i,j] = -np.dot(L[i,j:i],L[j:i,j])/L[i,i]
L[n-1,n-1] = 1.0/L[n-1,n-1]
n = len(a)
L = choleski(b)
invert(L)
h = np.dot(b,np.inner(a,L))
return h,np.transpose(L)
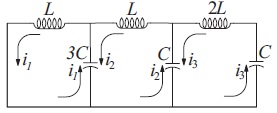
(1) Show that the analysis of the electric circuit shown leads to a matrix eigenvalue problem. (2) Determine the circular frequencies and the relative amplitudes of the currents.

Solution:

The circular frequencies are given by \( w_{i}=\sqrt{\lambda _{i}/LC} \)
## example9_3
# Determine the circular frequencies and the relative amplitudes of the
# currents.
import numpy
from jacobi import *
import math
from sortJacobi import *
from stdForm import *
A = np.array([[ 1/3, -1/3, 0.0], \
[-1/3, 4/3, -1.0], \
[ 0.0, -1.0, 2.0]])
B = np.array([[1.0, 0.0, 0.0], \
[0.0, 1.0, 0.0], \
[0.0, 0.0, 2.0]])
H,T = stdForm(A,B) # Transform into std. form
lam,Z = jacobi(H) # Z = eigenvecs. of H
X = np.dot(T,Z) # Eigenvecs. of original problem
sortJacobi(lam,X) # Arrange in ascending order of eigenvecs.
for i in range(3): # Normalize eigenvecs.
X[:,i] = X[:,i]/math.sqrt(np.dot(X[:,i],X[:,i]))
print('Eigenvalues:\n',lam)
print('Eigenvectors:\n',X)
input ("Press return to exit")
## module inversePower
''' lam,x = inversePower(a,s,tol=1.0e-6).
Inverse power method for solving the eigenvalue problem
[a]{x} = lam{x}. Returns 'lam' closest to 's' and the
corresponding eigenvector {x}.
'''
import numpy as np
from LUdecomp import *
import math
from random import random
def inversePower(a,s,tol=1.0e-6):
n = len(a)
aStar = a - np.identity(n)*s # Form [a*] = [a] - s[I]
aStar = LUdecomp(aStar) # Decompose [a*]
x = np.zeros(n)
for i in range(n): # Seed [x] with random numbers
x[i] = random()
xMag = math.sqrt(np.dot(x,x)) # Normalize [x]
x =x/xMag
for i in range(50): # Begin iterations
xOld = x.copy() # Save current [x]
x = LUsolve(aStar,x) # Solve [a*][x] = [xOld]
xMag = math.sqrt(np.dot(x,x)) # Normalize [x]
x = x/xMag
if np.dot(xOld,x) < 0.0: # Detect change in sign of [x]
sign = -1.0
x = -x
else: sign = 1.0
if math.sqrt(np.dot(xOld - x,xOld - x)) < tol:
return s + sign/xMag,x
print('Inverse power method did not converge')
## example9_4
# The stress matrix describing the state of stress at a point is
# S =[−30 10 20
# 10 40 −50
# 20 −50 −10]MPa
# Determine the largest principal stress (the eigenvalue of S farthest from zero) by the
# power method
import numpy as np
import math
s = np.array([[-30.0, 10.0, 20.0], \
[ 10.0, 40.0, -50.0], \
[ 20.0, -50.0, -10.0]])
v = np.array([1.0, 0.0, 0.0])
for i in range(100):
vOld = v.copy()
z = np.dot(s,v)
zMag = math.sqrt(np.dot(z,z))
v = z/zMag
if np.dot(vOld,v) < 0.0:
sign = -1.0
v = -v
else: sign = 1.0
if math.sqrt(np.dot(vOld - v,vOld - v)) < 1.0e-6: break
lam = sign*zMag
print("Number of iterations =",i)
print("Eigenvalue =",lam)
input("Press return to exit")
## example9_5
# Determine the smallest eigenvalue λ1 and the corresponding eigenvector of
# A =[11 2 3 1 4
# 2 9 3 5 2
# 3 3 15 4 3
# 1 5 4 12 4
# 4 2 3 4 17]
# Use the inverse power method with eigenvalue shifting knowing that λ1 ≈ 5
import numpy as np
from inversePower import *
s = 5.0
a = np.array([[ 11.0, 2.0, 3.0, 1.0, 4.0], \
[ 2.0, 9.0, 3.0, 5.0, 2.0], \
[ 3.0, 3.0, 15.0, 4.0, 3.0], \
[ 1.0, 5.0, 4.0, 12.0, 4.0], \
[ 4.0, 2.0, 3.0, 4.0, 17.0]])
lam,x = inversePower(a,s)
print("Eigenvalue =",lam)
print("\nEigenvector:\n",x)
input("\nPrint press return to exit")
## module inversePower5
''' lam,x = inversePower5(Bv,d,e,f,tol=1.0e-6).
Inverse power method for solving the eigenvalue problem
[A]{x} = lam[B]{x}, where [A] is pentadiagonal and [B]
is sparse. User must supply the function Bv(v) that
returns the vector [B]{v}.
'''
import numpy as np
from LUdecomp5 import *
import math
from numpy.random import rand
def inversePower5(Bv,d,e,f,tol=1.0e-6):
n = len(d)
d,e,f = LUdecomp5(d,e,f)
x = rand(n) # Seed x with random numbers
xMag = math.sqrt(np.dot(x,x)) # Normalize {x}
x = x/xMag
for i in range(30): # Begin iterations
xOld = x.copy() # Save current {x}
x = Bv(xOld) # Compute [B]{x}
x = LUsolve5(d,e,f,x) # Solve [A]{z} = [B]{x}
xMag = math.sqrt(np.dot(x,x)) # Normalize {z}
x = x/xMag
if np.dot(xOld,x) < 0.0: # Detect change in sign of {x}
sign = -1.0
x = -x
else: sign = 1.0
if math.sqrt(np.dot(xOld - x,xOld - x)) < tol:
return sign/xMag,x
print('Inverse power method did not converge')
The propped cantilever beam carries a compressive axial load P. The lateral displacement
u(x) of the beam can be shown to satisfy the differential equation
$$ u^{(4)}+\frac{P}{EI}{u}''=0 $$
where EI is the bending rigidity. The boundary conditions are
u(0) = u''(0) = 0 u(L) = u'(L) = 0
(1) Show that buckling analysis of the beam results in a matrix eigenvalue problem if
the derivatives are approximated by finite differences. (2)Write a program that computes
the smallest buckling load of the beam, making full use of banded matrices.
Run the program with 100 interior nodes (n = 100)

Solution:


## example9_6
import numpy as np
from inversePower5 import *
def Bv(v): # Compute {z} = [B]{v}
n = len(v)
z = np.zeros(n)
z[0] = 2.0*v[0] - v[1]
for i in range(1,n-1):
z[i] = -v[i-1] + 2.0*v[i] - v[i+1]
z[n-1] = -v[n-2] + 2.0*v[n-1]
return z
n = 100 # Number of interior nodes
d = np.ones(n)*6.0 # Specify diagonals of [A] = [f\e\d\e\f]
d[0] = 5.0
d[n-1] = 7.0
e = np.ones(n-1)*(-4.0)
f = np.ones(n-2)*1.0
lam,x = inversePower5(Bv,d,e,f)
print("PLˆ2/EI =",lam*(n+1)**2)
input("\nPress return to exit")
## module householder
''' d,c = householder(a).
Householder similarity transformation of matrix [a] to
tridiagonal form].
p = computeP(a).
Computes the acccumulated transformation matrix [p]
after calling householder(a).
'''
import numpy as np
import math
def householder(a):
n = len(a)
for k in range(n-2):
u = a[k+1:n,k]
uMag = math.sqrt(np.dot(u,u))
if u[0] < 0.0: uMag = -uMag
u[0] = u[0] + uMag
h = np.dot(u,u)/2.0
v = np.dot(a[k+1:n,k+1:n],u)/h
g = np.dot(u,v)/(2.0*h)
v = v - g*u
a[k+1:n,k+1:n] = a[k+1:n,k+1:n] - np.outer(v,u) \
- np.outer(u,v)
a[k,k+1] = -uMag
return np.diagonal(a),np.diagonal(a,1)
def computeP(a):
n = len(a)
p = np.identity(n)*1.0
for k in range(n-2):
u = a[k+1:n,k]
h = np.dot(u,u)/2.0
v = np.dot(p[1:n,k+1:n],u)/h
p[1:n,k+1:n] = p[1:n,k+1:n] - np.outer(v,u)
return p
## example9_8
# Use the function householder to tridiagonalize the matrix
# A =[7 2 3 −1
# 2 8 5 1
# 3 5 12 9
# −1 1 9 7]
# also determine the transformation matrix P.
import numpy as np
from householder import *
a = np.array([[ 7.0, 2.0, 3.0, -1.0], \
[ 2.0, 8.0, 5.0, 1.0], \
[ 3.0, 5.0, 12.0, 9.0], \
[-1.0, 1.0, 9.0, 7.0]])
d,c = householder(a)
print("Principal diagonal {d}:\n", d)
print("\nSubdiagonal {c}:\n",c)
print("\nTransformation matrix [P]:")
print(computeP(a))
input("\nPress return to exit")
## module sturmSeq
''' p = sturmSeq(c,d,lam).
Returns the Sturm sequence {p[0],p[1],...,p[n]}
associated with the characteristic polynomial
|[A] - lam[I]| = 0, where [A] is a n x n
tridiagonal matrix.
numLam = numLambdas(p).
Returns the number of eigenvalues of a tridiagonal
matrix that are smaller than 'lam'.
Uses the Sturm sequence {p} obtained from 'sturmSeq'.
'''
import numpy as np
def sturmSeq(d,c,lam):
n = len(d) + 1
p = np.ones(n)
p[1] = d[0] - lam
for i in range(2,n):
p[i] = (d[i-1] - lam)*p[i-1] - (c[i-2]**2)*p[i-2]
return p
def numLambdas(p):
n = len(p)
signOld = 1
numLam = 0
for i in range(1,n):
if p[i] > 0.0: sign = 1
elif p[i] < 0.0: sign = -1
else: sign = -signOld
if sign*signOld < 0: numLam = numLam + 1
signOld = sign
return numLam
## module gerschgorin
''' lamMin,lamMax = gerschgorin(d,c).
Applies Gerschgorin's theorem to find the global bounds on
the eigenvalues of a symmetric tridiagonal matrix.
'''
def gerschgorin(d,c):
n = len(d)
lamMin = d[0] - abs(c[0])
lamMax = d[0] + abs(c[0])
for i in range(1,n-1):
lam = d[i] - abs(c[i]) - abs(c[i-1])
if lam < lamMin: lamMin = lam
lam = d[i] + abs(c[i]) + abs(c[i-1])
if lam > lamMax: lamMax = lam
lam = d[n-1] - abs(c[n-2])
if lam < lamMin: lamMin = lam
lam = d[n-1] + abs(c[n-2])
if lam > lamMax: lamMax = lam
return lamMin,lamMax
## module lamRange
''' r = lamRange(d,c,N).
Returns the sequence {r[0],r[1],...,r[N]} that
separates the N lowest eigenvalues of the tridiagonal
matrix; that is, r[i] < lam[i] < r[i+1].
'''
import numpy as np
from sturmSeq import *
from gerschgorin import *
def lamRange(d,c,N):
lamMin,lamMax = gerschgorin(d,c)
r = np.ones(N+1)
r[0] = lamMin
# Search for eigenvalues in descending order
for k in range(N,0,-1):
# First bisection of interval(lamMin,lamMax)
lam = (lamMax + lamMin)/2.0
h = (lamMax - lamMin)/2.0
for i in range(1000):
# Find number of eigenvalues less than lam
p = sturmSeq(d,c,lam)
numLam = numLambdas(p)
# Bisect again & find the half containing lam
h = h/2.0
if numLam < k: lam = lam + h
elif numLam > k: lam = lam - h
else: break
# If eigenvalue located, change the upper limit
# of search and record it in [r]
lamMax = lam
r[k] = lam
return r
## module eigenvals3
''' lam = eigenvals3(d,c,N).
Returns the N smallest eigenvalues of a symmetric
tridiagonal matrix defined by its diagonals d and c.
'''
from lamRange import *
from ridder import *
from sturmSeq import sturmSeq
from numpy import zeros
def eigenvals3(d,c,N):
def f(x): # f(x) = |[A] - x[I]|
p = sturmSeq(d,c,x)
return p[len(p)-1]
lam = zeros(N)
r = lamRange(d,c,N) # Bracket eigenvalues
for i in range(N): # Solve by Brent's method
lam[i] = ridder(f,r[i],r[i+1])
return lam
## example9_12
# Use eigenvals3 to determine the three smallest eigenvalues of the 100 × 100 matrix:
# A =[2 −1 0 · · · 0
# −1 2 −1 · · · 0
# 0 −1 2 · · · 0
# . . . .
# . . . .
# . . . .
# 0 0 · · · −1 2]
import numpy as np
from eigenvals3 import *
N = 3
n = 100
d = np.ones(n)*2.0
c = np.ones(n-1)*(-1.0)
lambdas = eigenvals3(d,c,N)
print (lambdas)
input("\nPress return to exit")
## module inversePower3
''' lam,x = inversePower3(d,c,s,tol=1.0e-6)
Inverse power method applied to a symmetric tridiagonal
matrix. Returns the eigenvalue closest to s
and the corresponding eigenvector.
'''
from LUdecomp3 import *
import math
import numpy as np
from numpy.random import rand
def inversePower3(d,c,s,tol=1.0e-6):
n = len(d)
e = c.copy()
cc = c.copy()
dStar = d - s # Form [A*] = [A] - s[I]
LUdecomp3(cc,dStar,e) # Decompose [A*]
x = rand(n) # Seed x with random numbers
xMag = math.sqrt(np.dot(x,x)) # Normalize [x]
x = x/xMag
for i in range(30): # Begin iterations
xOld = x.copy() # Save current [x]
LUsolve3(cc,dStar,e,x) # Solve [A*][x] = [xOld]
xMag = math.sqrt(np.dot(x,x)) # Normalize [x]
x = x/xMag
if np.dot(xOld,x) < 0.0: # Detect change in sign of [x]
sign = -1.0
x = -x
else: sign = 1.0
if math.sqrt(np.dot(xOld - x,xOld - x)) < tol:
return s + sign/xMag,x
print('Inverse power method did not converge')
return
## example9_13
# Compute the 10th smallest eigenvalue of the matrix:
# A =[2 −1 0 · · · 0
# −1 2 −1 · · · 0
# 0 −1 2 · · · 0
# . . . .
# . . . .
# . . . .
# 0 0 · · · −1 2]
import numpy as np
from lamRange import *
from inversePower3 import *
N = 10
n = 100
d = np.ones(n)*2.0
c = np.ones(n-1)*(-1.0)
r = lamRange(d,c,N) # Bracket N smallest eigenvalues
s = (r[N-1] + r[N])/2.0 # Shift to midpoint of Nth bracket
lam,x = inversePower3(d,c,s) # Inverse power method
print("Eigenvalue No.",N," =",lam)
input("\nPress return to exit")
## example9_14
# Compute the three smallest eigenvalues and the corresponding eigenvectors of the
# matrix
# A = [11 2 3 1 4
# 2 9 3 5 2
# 3 3 15 4 3
# 1 5 4 12 4
# 4 2 3 4 17]
from householder import *
from eigenvals3 import *
from inversePower3 import *
import numpy as np
N = 3 # Number of eigenvalues requested
a = np.array([[ 11.0, 2.0, 3.0, 1.0, 4.0], \
[ 2.0, 9.0, 3.0, 5.0, 2.0], \
[ 3.0, 3.0, 15.0, 4.0, 3.0], \
[ 1.0, 5.0, 4.0, 12.0, 4.0], \
[ 4.0, 2.0, 3.0, 4.0, 17.0]])
xx = np.zeros((len(a),N))
d,c = householder(a) # Tridiagonalize [A]
p = computeP(a) # Compute transformation matrix
lambdas = eigenvals3(d,c,N) # Compute eigenvalues
for i in range(N):
s = lambdas[i]*1.0000001 # Shift very close to eigenvalue
lam,x = inversePower3(d,c,s) # Compute eigenvector [x]
xx[:,i] = x # Place [x] in array [xx]
xx = np.dot(p,xx) # Recover eigenvectors of [A]
print("Eigenvalues:\n",lambdas)
print("\nEigenvectors:\n",xx)
input("Press return to exit")