## module goldSearch
''' a,b = bracket(f,xStart,h)
Finds the brackets (a,b) of a minimum point of the
user-supplied scalar function f(x).
The search starts downhill from xStart with a step
length h.
x,fMin = search(f,a,b,tol=1.0e-6)
Golden section method for determining x that minimizes
the user-supplied scalar function f(x).
The minimum must be bracketed in (a,b).
'''
import math
def bracket(f,x1,h):
c = 1.618033989
f1 = f(x1)
x2 = x1 + h; f2 = f(x2)
# Determine downhill direction and change sign of h if needed
if f2 > f1:
h = -h
x2 = x1 + h; f2 = f(x2)
# Check if minimum between x1 - h and x1 + h
if f2 > f1: return x2,x1 - h
# Search loop
for i in range (100):
h = c*h
x3 = x2 + h; f3 = f(x3)
if f3 > f2: return x1,x3
x1 = x2; x2 = x3
f1 = f2; f2 = f3
print("Bracket did not find a mimimum")
def search(f,a,b,tol=1.0e-9):
nIter = int(math.ceil(-2.078087*math.log(tol/abs(b-a))))
R = 0.618033989
C = 1.0 - R
# First telescoping
x1 = R*a + C*b; x2 = C*a + R*b
f1 = f(x1); f2 = f(x2)
# Main loop
for i in range(nIter):
if f1 > f2:
a = x1
x1 = x2; f1 = f2
x2 = C*a + R*b; f2 = f(x2)
else:
b = x2
x2 = x1; f2 = f1
x1 = R*a + C*b; f1 = f(x1)
if f1 < f2: return x1,f1
else: return x2,f2
## example10_1
# Use goldSearch to find x that minimizes
# f (x) = 1.6x^3 + 3x^2 − 2x
# subject to the constraint x >= 0. Compare the result with the analytical solution
#(the global minimum occurs at x = 0.273494)
from goldSearch import *
def f(x):
lam = 1.0 # Constraint multiplier
c = min(0.0, x) # Constraint function
return 1.6*x**3 + 3.0*x**2 - 2.0*x + lam*c**2
xStart = 1.0
h = 0.01
x1,x2 = bracket(f,xStart,h)
x,fMin = search(f,x1,x2)
print("x =",x)
print("f(x) =",fMin)
input ("\nPress return to exit")
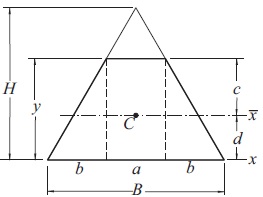
The trapezoid shown below is the cross section of a beam. It is formed by removing the top from a triangle of base B = 48mm and height H = 60 mm. The problem is to find the height y of the trapezoid that maximizes the section modulus \(S=I_{\bar{x}}/c \) where \(I_{\bar{x}}\) is the second moment of the cross-sectional area about the axis that passes through the centroid C of the cross section. By optimizing the section modulus, we minimize the maximum bending stress σmax = M/S in the beam, M being the bending moment.

Solution: Considering the area of the trapezoid as a composite of a rectangle and two triangles, the section modulus is found through the following sequence of computations:
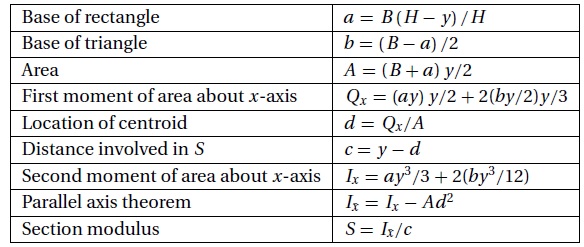
Because we wish to maximize S with a minimization algorithm, the merit function is −S. There are no constraints in this problem.
## example10_2
# calculates the height y of a trapezoid that maximizes the section modulus cross section of a beam
from goldSearch import *
def f(y):
B = 48.0
H = 60.0
a = B*(H - y)/H
b = (B - a)/2.0
A = (B + a)*y/2.0
Q = (a*y**2)/2.0 + (b*y**2)/3.0
d = Q/A
c = y - d
I = (a*y**3)/3.0 + (b*y**3)/6.0
Ibar = I - A*d**2
return -Ibar/c
yStart = 60.0 # Starting value of y
h = 1.0 # Size of first step used in bracketing
a,b = bracket(f,yStart,h)
yOpt,fOpt = search(f,a,b)
print("Optimal y =",yOpt)
print("Optimal S =",-fOpt)
print("S of triangle =",-f(60.0))
input("Press return to exit")
## module powell
''' xMin,nCyc = powell(F,x,h=0.1,tol=1.0e-6)
Powell's method of minimizing user-supplied function F(x).
x = starting point
h = initial search increment used in 'bracket'
xMin = mimimum point
nCyc = number of cycles
'''
import numpy as np
from goldSearch import *
import math
def powell(F,x,h=0.1,tol=1.0e-6):
def f(s): return F(x + s*v) # F in direction of v
n = len(x) # Number of design variables
df = np.zeros(n) # Decreases of F stored here
u = np.identity(n) # Vectors v stored here by rows
for j in range(30): # Allow for 30 cycles:
xOld = x.copy() # Save starting point
fOld = F(xOld)
# First n line searches record decreases of F
for i in range(n):
v = u[i]
a,b = bracket(f,0.0,h)
s,fMin = search(f,a,b)
df[i] = fOld - fMin
fOld = fMin
x = x + s*v
# Last line search in the cycle
v = x - xOld
a,b = bracket(f,0.0,h)
s,fLast = search(f,a,b)
x = x + s*v
# Check for convergence
if math.sqrt(np.dot(x-xOld,x-xOld)/n) < tol: return x,j+1
# Identify biggest decrease & update search directions
iMax = np.argmax(df)
for i in range(iMax,n-1):
u[i] = u[i+1]
u[n-1] = v
print("Powell did not converge")
## example10_3
# Find the minimum of the function
# F = 100(y − x^2)^2 + (1 − x)^2
from powell import *
from numpy import array
def F(x): return 100.0*(x[1] - x[0]**2)**2 + (1 - x[0])**2
xStart = array([-1.0, 1.0])
xMin,nIter = powell(F,xStart)
print("x =",xMin)
print("F(x) =",F(xMin))
print("Number of cycles =",nIter)
input ("Press return to exit")
Use powell to determine the smallest distance from the point (5, 8) to the curve
xy = 5.
Solution: This is a constrained optimization problem:Minimize F(x, y) = (x − 5)^2 + (y − 8)^2
(the square of the distance) subject to the equality constraint xy − 5 = 0.
## example10_4
# Use powell to determine the smallest distance from the point (5, 8) to the curve
# xy = 5
from powell import *
from numpy import array
from math import sqrt
def F(x):
lam = 1.0 # Penalty multiplier
c = x[0]*x[1] - 5.0 # Constraint equation
return distSq(x) + lam*c**2 # Penalized merit function
def distSq(x): return (x[0] - 5)**2 + (x[1] - 8)**2
xStart = array([ 1.0,5.0])
x,numIter = powell(F,xStart,0.1)
print("Intersection point =",x)
print("Minimum distance =", sqrt(distSq(x)))
print("xy =", x[0]*x[1])
print("Number of cycles =",numIter)
input ("Press return to exit")
Check: Since we have an equality constraint, the optimal point can readily be found
by calculus. The function is (here λ is the Lagrangian multiplier)
F*(x, y, λ) = (x − 5)2 + (y − 8)2 + λ(xy − 5) so we derive:
∂F*/∂x = 2(x − 5) + λy = 0
∂F*/∂y = 2(y − 8) + λx = 0
g(x) = xy − 5 = 0
which can be solved with the Newton-Raphson method
## example10_4_check
import numpy as np
from newtonRaphson2 import *
def F(x):
return np.array([2.0*(x[0] - 5.0) + x[2]*x[1], \
2.0*(x[1] - 8.0) + x[2]*x[0], \
x[0]*x[1] - 5.0])
xStart = np.array([1.0, 5.0, 1.0])
print("x = ", newtonRaphson2(F,xStart))
input("Press return to exit")
The displacement formulation of the truss shown results in the following simultaneous
equations for the joint displacements u:
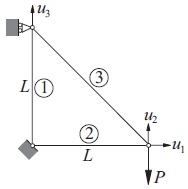
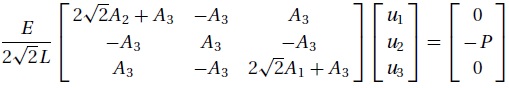
where E represents the modulus of elasticity of the material and Ai is the cross sectional
area of member i. Use Powell’s method to minimize the structural volume
(the weight) of the truss while keeping the displacement u2 below a given
value δ.
## example10_5
# minimize the structural volume(the weight) of the truss
from powell import *
from numpy import array
from math import sqrt
from gaussElimin import *
def F(x):
global v, weight
lam = 100.0
c = 2.0*sqrt(2.0)
A = array([[c*x[1] + x[2], -x[2], x[2]], \
[-x[2], x[2], -x[2]], \
[ x[2], -x[2], c*x[0] + x[2]]])/c
b = array([0.0, -1.0, 0.0])
v = gaussElimin(A,b)
weight = x[0] + x[1] + sqrt(2.0)*x[2]
penalty = max(0.0,abs(v[1]) - 1.0)**2 \
+ max(0.0,-x[0])**2 \
+ max(0.0,-x[1])**2 \
+ max(0.0,-x[2])**2
return weight + penalty*lam
xStart = array([1.0, 1.0, 1.0])
x,numIter = powell(F,xStart)
print("x = ",x)
print("v = ",v)
print("Relative weight F = ",weight)
print("Number of cycles = ",numIter)
input("Press return to exit")
## module downhill
''' x = downhill(F,xStart,side=0.1,tol=1.0e-6)
Downhill simplex method for minimizing the user-supplied
scalar function F(x) with respect to the vector x.
xStart = starting vector x.
side = side length of the starting simplex (default is 0.1)
'''
import numpy as np
import math
def downhill(F,xStart,side=0.1,tol=1.0e-6):
n = len(xStart) # Number of variables
x = np.zeros((n+1,n))
f = np.zeros(n+1)
# Generate starting simplex
x[0] = xStart
for i in range(1,n+1):
x[i] = xStart
x[i,i-1] = xStart[i-1] + side
# Compute values of F at the vertices of the simplex
for i in range(n+1): f[i] = F(x[i])
# Main loop
for k in range(500):
# Find highest and lowest vertices
iLo = np.argmin(f)
iHi = np.argmax(f)
# Compute the move vector d
d = (-(n+1)*x[iHi] + np.sum(x,axis=0))/n
# Check for convergence
if math.sqrt(np.dot(d,d)/n) < tol: return x[iLo]
# Try reflection
xNew = x[iHi] + 2.0*d
fNew = F(xNew)
if fNew <= f[iLo]: # Accept reflection
x[iHi] = xNew
f[iHi] = fNew
# Try expanding the reflection
xNew = x[iHi] + d
fNew = F(xNew)
if fNew <= f[iLo]: # Accept expansion
x[iHi] = xNew
f[iHi] = fNew
else:
# Try reflection again
if fNew <= f[iHi]: # Accept reflection
x[iHi] = xNew
f[iHi] = fNew
else:
# Try contraction
xNew = x[iHi] + 0.5*d
fNew = F(xNew)
if fNew <= f[iHi]: # Accept contraction
x[iHi] = xNew
f[iHi] = fNew
else:
# Use shrinkage
for i in range(len(x)):
if i != iLo:
x[i] = (x[i] - x[iLo])*0.5
f[i] = F(x[i])
print("Too many iterations in downhill")
return x[iLo]
The figure shows the cross section of a channel carrying water. Use the downhill simplex to determine h, b, and θ that minimize the length of the wetted perimeter while maintaining a cross-sectional area of 8m2. (Minimizing the wetted perimeter results in the least resistance to the flow.)
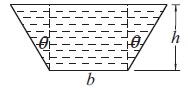
Solution: The cross-sectional area of the channel is
A = 1/2[b + (b + 2htan θ)]h = (b + htan θ)h
the length of the wetted perimeter is
S = b + 2(hsec θ)
The optimization problem is to minimize S subject to the constraint A − 8 = 0. Using
the penalty function to take care of the equality constraint, the function to be
minimized is
S* = b + 2hsec θ + λ[(b + htan θ)h − 8]2
## example10_7
# minimize the length of the wetted perimeter
import numpy as np
import math
from downhill import *
def S(x):
global perimeter,area
lam = 10000.0
perimeter = x[0] + 2.0*x[1]/math.cos(x[2])
area = (x[0] + x[1]*math.tan(x[2]))*x[1]
return perimeter + lam*(area - 8.0)**2
xStart = np.array([4.0, 2.0, 0.0])
x = downhill(S,xStart)
area = (x[0] + x[1]*math.tan(x[2]))*x[1]
print("b = ",x[0])
print("h = ",x[1])
print("theta (deg) = ",x[2]*180.0/math.pi)
print("area = ",area)
print("perimeter = ",perimeter)
input("Finished. Press return to exit")
The fundamental circular frequency of the stepped shaft shown is required to be higher than
ω0 (a given value). Use the downhill simplex to determine the diameters d1
and d2
that minimize the volume of the material without violating the frequency constraint.
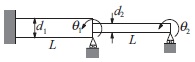
The approximate value of the fundamental frequency can be computed by solving
the eigenvalue problem (obtainable from the finite element approximation)

Solution: We start by introducing the dimensionless variables xi = di/d0,
where d0 is
an arbitrary “base” diameter. As a result, the eigenvalue problem becomes
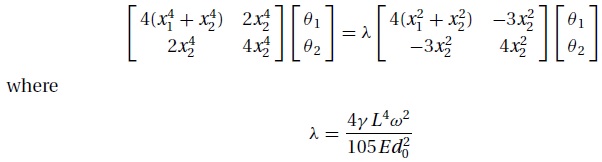
## example10_8
# Use the downhill simplex to determine the diameters d1 and d2
# that minimize the volume of the material without violating the
# frequency constraint.
import numpy as np
from stdForm import *
from inversePower import *
from downhill import *
def F(x):
global eVal
lam = 1.0e6
eVal_min = 0.4
A = np.array([[4.0*(x[0]**4 + x[1]**4), 2.0*x[1]**4], \
[2.0*x[1]**4, 4.0*x[1]**4]])
B = np.array([[4.0*(x[0]**2 + x[1]**2), -3.0*x[1]**2], \
[-3*x[1]**2, 4.0*x[1]**2]])
H,t = stdForm(A,B)
eVal,eVec = inversePower(H,0.0)
return x[0]**2 + x[1]**2 + lam*(max(0.0,eVal_min - eVal))**2
xStart = np.array([1.0,1.0])
x = downhill(F,xStart,0.1)
print("x = ", x)
print("eigenvalue = ",eVal)
input ("Press return to exit")