Los vectores u e v se dice que son ortogonales si y
solamente si su producto escalar es cero, es decir,
u•v=0
|
En
ℝ
n
con el producto escalar euclídeo, si dos
vectores no nulos u y v son ortogonales entonces el ángulo entre
u y
v es
π
2
.
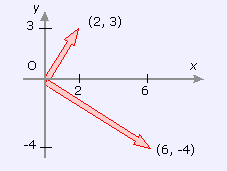
Por ejemplo en
ℝ
2
los dos vectores del gráfico son ortogonales:
(
2,3
)•(
6,−4
)=0
En el siguiente gráfico puedes introducir las coordenadas
x e y
de los vectores u y v de
ℝ
2
, y comprobar si son ortogonales:
|
Una base
{
v
1
,
v
2
,...,
v
n
}
de
E
n
se dice ortonormal si y solamente sí todos son vectores son de norma 1 y dos a
dos son ortogonales.
|
Por
ejemplo la base canónica,
{
e
1
,
e
2
,...,
e
n
}
es una base ortonormal de
E
n
.
|