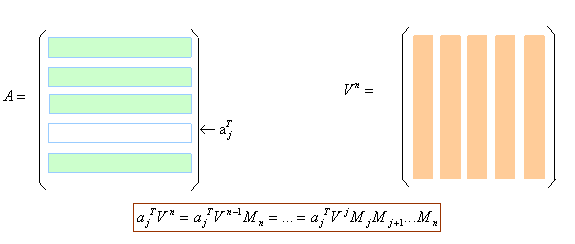
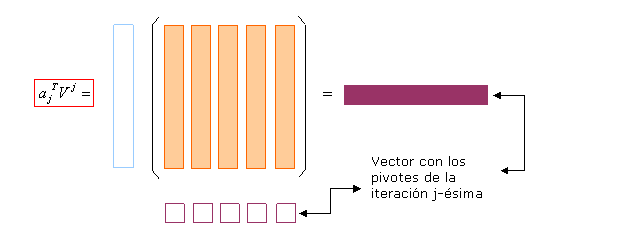En cada paso del método propuesto anteriormente se
obtiene una matriz que es el producto de la matriz del paso anterior por
matrices elementales.
Si se denota por
V
j
,
a la matriz de partida en el paso j-ésimo, la matriz que se obtiene es
V
j+1
=
V
j
M
j
donde
M
j
es producto de matrices elementales.
Por ejemplo, en el segundo paso, j=2, se tiene una vez calculados los
pivotes:
V
2
=
(
1
0
−1
1
−1
0
0
1
1
−1
−1
1
0
0
−1
0
)
pivote→
3
0
2
−1
→
transformación
V
3
=(
−1/2
−1
1/2
1/2
3/2
0
−1/2
−1/2
1/2
0
−1/2
−3/2
−1/2
1
1/2
1/2
)
V
3
=
V
2
M
2
siendo
M
2
=(
1
0
0
0
0
1
0
0
−3/2
0
1/2
1/2
0
0
0
1
)
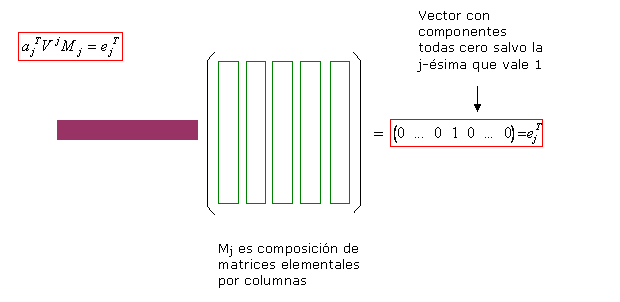
La matriz
M
2
es el producto de cuatro matrices elementales
M
2
=
(
1
0
0
0
0
1
0
0
0
0
1/2
0
0
0
0
1
)
︸
C
3
(
2
)
(
1
0
0
0
0
1
0
0
−3
0
1
0
0
0
0
1
)
︸
C
13
(
−1
)
(
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
)
︸
C
23
(
0
)
(
1
0
0
0
0
1
0
0
0
0
1
−1
0
0
0
1
)
︸
C
43
(
1
)
=(
1
0
0
0
0
1
0
0
−3/2
0
1/2
1/2
0
0
0
1
)
|