Métodos numéricos
Elena E. Álvarez Saiz
Red Educativa Digital Descartes.
Universidad de Cantabria
Título de la obra:
Métodos numéricos
Autora:
Elena E. Alvarez Saiz
Diseño del libro: Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Primera Edición
LICENCIA
Tabla de contenido
Prefacio
Cuestiones básicas sobre
aritmética computacional
Introducción
En un curso de cálculo numérico se estudian por lo general métodos o modelos matemáticos que permiten hallar la solución numérica a problemas relacionados entre otros con Ecuaciones diferenciales, Integrales definidas, Sistemas de ecuaciones simultáneas, Raíces de ecuaciones, Interpolación. Como criterio general de trabajo, el objetivo será llegar a la solución correcta (con un error aceptable) de forma eficiente (en un tiempo razonable).
En la aproximación de un fenómeno físico mediante un modelo matemático y su posterior solución numérica, se cometen diferentes clases de errores. Algunos de ellos se debe a errores en los datos iniciales (por ejemplo de medida con algún instrumento), errores de discretización del problema, errores de redondeo debidos a la forma en la que el computador almacena los números, etc. El objetivo de este tema es analizar este último tipo de errores.
Algunos ejemplos de situaciones reales provocadas por errores computacionales
Misiles Patriot
El 25 de febrero de 1991, durante la Guerra del Golfo, una batería de misiles Patriot estadounidense en Dharan, Arabia Saudita, no pudo interceptar un misil Scud iraquí entrante. El Scud atacó un cuartel del ejército estadounidense y mató a 28 soldados.
Un informe de la entonces Oficina General de Contabilidad titulado "Patriot Missile Defense: Problema de software conducido a una falla del sistema en Dhahran, Arabia Saudita" informó sobre la causa del fallo: un cálculo inexacto del tiempo desde el inicio debido a errores aritméticos del computador.

Específicamente, el tiempo en décimas de segundo, medido por el reloj interno del sistema, se multiplicó por 10 para producir el tiempo en segundos. Este cálculo se realizó utilizando un registro de punto fijo de 24 bits. En particular, el valor 1/10, que tiene una expansión binaria infinita, se cortó a 24 bits después del punto de base. El pequeño error de corte, cuando se multiplica por el gran número que da el tiempo en décimas de segundo, conduce a un error significativo Douglas N. Arnold, “ The Patriot Missile Failure ,” Institute for Mathematics and its Applications,Minneapolis (2000). Fuente http://www.ima.umn.edu/~arnold/disasters/patriot.html.
La explosión del cohete Ariane
El Programa Ariane, es un programa emprendido por Europa en 1973 para dotarse de un lanzador que le permitiera un acceso independiente al espacio.
El desarrollo del lanzador Ariane se efectúa bajo la dirección de la Agencia Espacial Europea (ESA, por sus siglas en inglés); el Centro Nacional de Estudios Espaciales(CNES) francés fue el contratista principal hasta mayo de 2003, fecha en la que pasó a actuar como tal el consorcio europeo EADS (European Aeronautic Defenceand Space Company). La explotación comercial es gestionada por la sociedad Arianespace, creada en 1980. En total, unas 40 compañías europeas están comprometidas en el desarrollo y construcción del lanzador Ariane.
Todos los lanzamientos se efectúan desde el centro espacial de Kourou, en la Guayana Francesa, que cuenta con varias rampas de lanzamiento, y en el que trabajan de forma permanente varios cientos de personas.
El 4 de junio de 1996, el cohete Ariane 5 Flight 501,de la Agencia Europea del Espacio (ESA) explotó 40 segundos después de su despegue a una altura de 3.7km. tras desviarse de la trayectoria prevista.

Era su primer viaje tras una década de investigación que costó más de 7000 millones de euros. El cohete y su carga estaban valorados en más de 500 millones de euros. La causa del error fue un fallo en el sistema de guiado de la trayectoria provocado 37 segundos después del despegue. Este error se produjo en el software que controlaba el sistema de referencia inercial (SRI).
En concreto, se produjo una excepción debido al intento de convertir un número en punto flotante de 64 bits, relacionado con la velocidad horizontal del cohete respecto de la plataforma de lanzamiento, en un entero con signo de 16 bits. El número mas grande que se puede representarde esta forma es 32767 Douglas N. Arnold, “ The Explosion of the Ariane 5 Rocket ,” Institute for Mathematics and its Applications,Minneapolis (2000). Fuente Fuente http://www.ima.umn.edu/~arnold/disasters/ariane.html.
Más información en: SIAM News, Vol. 29. Number 8, October 1996
El hundimiento de la plataforma petrolífera Sleipner A
El 23 de agosto de 1991, la plataforma petrolífera Sleipner A propiedad de la empresa noruega Statoil situada en el mar del Norte a 82 metros de profundidad se hundió. La causa del error fue un fallo en el modelado numérico de la plataforma utilizando elementos finitos. En concreto se produjo una fuga de agua en una de las paredes de uno de los 24 tanques de aire de 12 metros de diámetro que permitían la flotación de la plataforma de 57000 toneladas de peso que además soportaba a mas de 20 0personas y a equipamiento de extracción con un peso adicional de unas 40000 toneladas. Las bombas de extracción de agua no fueron capaces de evacuar toda el agua. El fallo tuvo un coste económico total de 700 millones de euros.
Para modelar los tanques de la plataforma se utilizó el programa NASTRAN de elementos finitos y una aproximación mediante un modelo elástico lineal. Esta aproximación no era correcta y subestimó en un 47% los esfuerzos que debían soportar las paredes de los tanques. En particular, ciertas paredes fueron diseñadas con un grosor insuficiente. Un análisis con elementos finitos correcto, pero posterior al accidente, demostró que el diseño de la plataforma provocaría fugas en algunas de los tanques cuando ésta estuviese sobre agua a 62 metros de profundidad.La fuga real se produjo cuando ésta estaba sobre 65 metros de agua, lo que ratifica la supuesta causa del fallo. Douglas N. Arnold, “ The sinking of the Sleipner A o®shore platform ,” Institute for Mathematics and itsApplications, Minneapolis (2000). Fuente http://www.ima.umn.edu/~arnold/disasters/sleipner.html.

Ejemplos de errores numéricos cometidos por el ordenador
El objetivo de este apartado es describir como el computador almacena los números y opera con ellos. Esto es fundamental para comprender los errores que comete durante este proceso y cómo afecta al resultado de un algoritmo numérico.
Ver ejemplo 1 a 6 de los apuntes.
Ejemplo. Analiza el siguiente código Matlab  .
.
for k=1:n
suma=suma+0.1;
end
format longEng;suma
El resultado debería ser $100$ pero se obtiene un número próximo a $100$: $99.9999999999986e+000$
Ejemplo. Analiza el siguiente código Matlab. 
g=@(x) x.^6-6 * x.^5+15 * x.^4-20 * x.^3+15 * x.^2-6 * x+1
x1=0.996:0.0001:1.005;format longEng;
[x1' f(x1)' g(x1)']
plot(x1,f(x1),x1,g(x1))
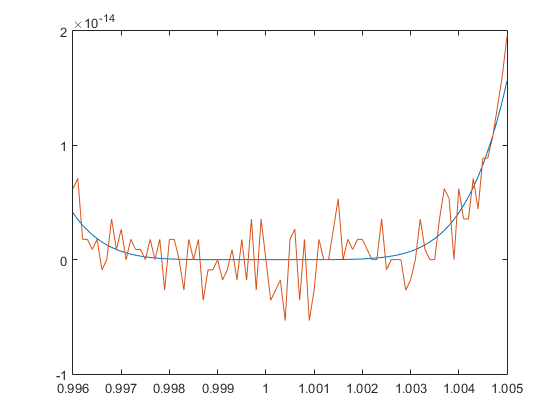
¿Por qué ocurre esto? La razón es que los ordenadores usan un formato (punto flotante binario) que no permite representar de forma precisa números como por ejemplo 0.1, 0.2 o 0.3. Dado que los números están, en general, representados de manera inexacta entonces las operaciones aritméticas también se hacen de manera inexacta.
Sistemas de numeración
Sistema decimal
En este sistema los números se representan utilizando 10 dígitos, es un sistema de numeración posicional en el que las cantidades se representan utilizando como base aritmética las potencias del número diez. Así,
$$x \in \mathbb{R}^{+} \,\,\,\,\, x = \sum\limits_{ - \infty }^n {{a_k} \cdot {{10}^k}} \,\,\,\,\, 0 \le {a_k} \le 9$$Ejemplo. Considera el número $709.3045$
Se puede escribir $$709.3045 = 7 \cdot {10^2} + 9 \cdot {10^0} + 3 \cdot {10^{ - 1}} + 4 \cdot {10^{ - 3}} + 5 \cdot {10^{ - 4}}$$
En general, si consideramos otra base $b$, un número real $x$ se puede escribir de la forma
$$x = \sum\limits_{ - \infty }^n {{a_k} \cdot {b^k}} \,\,\,\,\, 0 \le {a_k} \le b - 1$$ o también $$x = {a_n}{a_{n - 1}}...{a_0}.{a_{ - 1}}{a_{ - 2}}{a_{ - 3}}...$$Sistema binario
El Standard de IEEE propone el uso de la base 2 en el almacenamiento y la aritmética sobre el computador. En este sistema de numeración los números se representan utilizando solamente las cifras cero y uno (0 y 1)
$$x = \sum\limits_{ - \infty }^n {{a_k} \cdot {2^k}} \,\,\,\,\, 0 \le {a_k} \le 1$$Conversión de decimal a binario
El procedimiento es sencillo, basta dividir el número en base decimal y sus cocientes entre 2, acumulando los restos que conformarán el número en la nueva base. La lista de ceros y unos leídos de abajo a arriba darán la expresión en binario.
En la escena que se presenta a continuación, se muestra cómo hacer la conversión paso a paso para ciertos ejemplos. Este procedimiento es aplicable a cualquier base. En la escena se puede elegir números enteros y números con parte fraccionaria, observa el procedimiento para este último caso.
Ejemplo. Convierte $0.1_{10}$ a binario.
$$ \begin{aligned}{1 \over {10}} &= {1 \over {{2^4}}} + {1 \over {{2^5}}} + {0 \over {{2^6}}} + {0 \over {{2^7}}} + {1 \over {{2^8}}} + {1 \over {{2^9}}} + {0 \over {{2^6}}} + {0 \over {{2^7}}} + ... \\ &= 0001{\widehat {1001}_2} \end{aligned}$$
Conversión de binario a decimal
Puedes practicar con la siguiente herramienta interactiva introduciendo un número binario sin parte fraccionaria.
Ejemplo. Convierte el número $x=10.111001_2$ a decimal
Se tiene que: $$\begin{aligned} x = &1·2^1 + 0·2^0 + 1·2^{-1}+ 1·2^{-2} + \\ &+1·2^{-3}+ 0·2^{-4} + 0·2^{-5} + 1·2^{-6} \end{aligned}$$
Representación de los números reales en el computador
Un número en base 10 puede escribirse como
$$x = {\left( { - 1} \right)^s}× \,{10^e} × \,a.f$$donde
- s es el signo (0 si $x \ge 0$, 1 si $x < 0$)
- $1 \le a \le 9$
- $f = {f_1}{f_2}{f_3}...$ con $0 \le {f_i} \le 9$ para todo $i$
Se denomina:
- s signo
- e exponente
- f mantisa
Ejemplo. Considera el número $x=9028.304$ en base decimal.
Cuando la base es 2, el número se puede escribir
$$x = {\left( { - 1} \right)^s} × \,{2^e} × \,1.f$$Observa que para almacenar $x$ basta almacenar el signo $s$, el exponente $e$ y la mantisa $f$. No es necesario almacenar el 1 (bit oculto).
En el ordenador los números se almacenan en "palabras" de 32 bits (precisión sencilla), 64 bits (doble precisión) o 128 bits (precisión cuádruple). En Matlab la precisión que usaremos para los cálculos será doble precisión. En este caso se utiliza;
- 1 bit para el signo
- 52 bits para la mantisa
- 11 bits para el exponente

Teniendo en cuenta que el exponente se almacena en 11 bits, el valor mayor que se puede almacenar es:
$$\underbrace {0....0}_{11 \,bits}\,\,\,\,\,\,\,\,\text{hasta}\,\,\,\,\,,\,\underbrace {1....1}_{11 \,bits} \equiv 1 + 2 + ... + {2^{10}} = {2^{11}} - 1 = 2047$$Para poder considerar las potencias de 2 negativas se considera la siguiente representación normalizada en 64 bits:
$$x = \left( { - 1} \right)^s × 2^{e - 1023}× \,\,1.f \,\,\,\,\,\, \,\,\,\, 0 < e < 2047 $$- Cero: $e=0$, $f=0$.
- Infinito: $e=2047$, $f=0$.
- NAN: $e=2047$, $f \ne 0$.
Ejemplo. Almacenamiento del número $3.125_{10}$
Convirtiendo el exponente en binario, se tendrá $10000000000$. La mantisa ajustada a 52 bits es $1001\underbrace{0...0}_{48 \,\,bits}$.
El número se almacenerá de la forma: $$ \underbrace{0}_{signo} \underbrace{10000000000}_{exponente}\,\,\underbrace{10010...0}_{mantisa, \,48\,\,últimos \,\,bits\,\,0}$$
Herramientas de conversión
Rango y precisión
Dado que la representación de números reales bajo estos formatos es aproximada, hay dos conceptos importantes en la aritmética en punto flotante:
- Rango: Nos da el conjunto de intervalos donde existen números representables, este valor depende del exponente.
- Precisión: Nos da la diferencia entre dos números representables consecutivos, depende del número de bits de la mantisa.
Mayor número normalizado: realmax en Matlab
$${2^{1023}} × 1.\underbrace {1....1}_{52 \,\,bits} \equiv {2^{1023}}\left( {1 + \sum\limits_{j = 1}^{52} {{1 \over {{2^j}}}} } \right) \approx 1.79 \,× {10^{308}}$$Menor número estrictamente positivo normalizado: realmin en Matlab
$$2^{ - 1022} × 1.00...\underbrace 0_{bit\,\,52} \equiv {2^{ - 1022}} \approx 2.22 \,× {10^{-308}} $$Si consideramos que el bit escondido es cero, podemos obtener números menores que el mínimo número normalizado mediante la siguiente representación: $$x = \left( { - 1} \right)^s × 2^{- 1022} × \,\,0.f$$
Estos números se dicen que están desnormalizados.
Será $${2^{ - 1022}} \cdot 0.\underbrace {00...01}_{52\,bits} = {2^{ - 1022}} \cdot {2^{ - 52}} = {2^{ - 1074}}$$
Todos los números menores que este valor se consideran 0.
ans=
4.9407e-324
>>2^(-1075}
ans=
0
Precisión de la máquina: eps en Matlab
El número más pequeño que se puede representar después del 1 utilizando representación binaria en punto flotante con doble precisión es: $$1 = \left( { + 1} \right)× {{\rm{2}}^0}× 1.\underbrace {00...0}_{52}$$ $$1 + \varepsilon = \left( { + 1} \right)× {{\rm{2}}^0}× 1.\underbrace {00...01}_{52}$$
El valor de $\varepsilon$ es la precisión de la máquina:
$$\varepsilon = {2^{ - 52}}$$El número más pequeño $\varepsilon_M$ de forma que $1-\varepsilon_M \ne 1$: $$\varepsilon_M = {2^{ - 53}}$$
Operaciones en coma flotante
Para poder aplicar las operaciones matemáticas básicas a números representados por coma flotante se deben adecuar los números previamente.
Suma y resta: se alinean los bits (se aumenta la mantisa del número de menor exponente) y se suman o restan.
$$123456.7+101.7654$$ $$(1.234567×10^5)+(1.017654×10^2)=$$ $$(1.234567×10^5)+(0.001017654×10^5)=$$ $$(1.234567+0.001017654)×10^5=1.235584654×10^5$$
Multiplicación y división: se multiplican o dividen las mantisas y se suman o restan los exponentes.
Errores en un ordenador
El uso del computador para representar valores numéricos y operar con ellos, presenta ciertas limitaciones que no deben olvidarse y que por su importancia pasamos a tratar brevemente.
Error absoluto y relativo
Si $\widetilde p$ es una aproximación de $p$, se define:
- Error absoluto: $\left| {\widetilde p - p} \right|$
- Error relativo:${{\left| {\widetilde p - p} \right|} \over {\left| p \right|}}$
En general, en los métodos numéricos no se conoce el valor verdadero, por lo tanto tampoco el error real. Lo frecuente es tener una estimación del error dada por una cota positiva al tamaño máximo del error.
Cuestión. En 1862 el físico Foucault, utilizando un espejo giratorio, calculó en 298 000 km/s la velocidad de la luz. Aceptando como exacta la velocidad de 299 776 km/s, estimar el error absoluto y el error relativo cometido por Foucault. Por otra parte, la determinación de la constante universal h realizada por Planck en 1913 dio el valor de 6.41×10−27 erg seg. Adoptando el valor de 6.623×10−27 erg seg, estimar el error absoluto y relativo cometido por Planck. ¿Cuál de las dos medidas es más precisa?
Truncamiento y redondeo
Como se ha indicado anteriormente, las limitaciones de almacenamiento de bits generan cálculos aproximados de los números verdaderos, es decir, los números y errores están sujetos al sistema numérico de punto flotante. Si se considera el sistema decimal, un número real puede ser normalizado de la forma:
$$x = a.f_1f_2f_3...f_kf_{k+1}... × 10^e$$ $$1 \le f_i \le 9 \,\,\,\, \text{con}\,\,\,i = 1,2,3,4,...k$$El numero almacenado por el ordenador, que denotaremos por $fl(x)$ (de "floating") se obtiene terminando (recortando) la mantisa de $y$ en $k$ dígitos decimales. Existen dos métodos:
- Cortando los dígitos $f_{k+1}f_{k+2}...$ de forma que $fl(y) = a.f_1f_2f_3...f_k × 10^{e}$
- Redondeando el número
Si ($f_{k+1} \ge 5$) Entonces
Se agrega uno a $f_k$ para obtener $fl(y)$
FinSi
Si ($f_{k+1} < 5$) Entonces
Se cortan todos excepto los primeros k dígitos.
FinSi
Veamos algunos problemas que se producen al redondear los números almacenados por el computador.
Ejemplo. Calcula con Matlab la siguiente operación $1 - 3*(4/3 - 1)$. 
e =
2.2204e-16
Error por cancelación
Un caso frecuente de cancelación surge cuando se calcula la diferencia de dos números bastante próximos, y el redondeo del ordenador iguala esa diferencia a 0.
Ejemplo. Dados $x=1+2^{-54}$ e $y=1$, calcula con Matlab $x-y$ 
Nuestro ordenador establecerá que $x-y=0$ cuando en realidad $x - y \approx 5,5 \cdot {10^{ - 17}}$.
>>x=1+2^(-54);y=1;x-y
ans=
0
Ejemplo. Dados $x=2^{60}+2^6$ e $y=2^{60}$, calcula con Matlab $x-y$.
Matlab establecerá que $x-y=0$ cuando en realidad $x - y =64$.
>>x=2^60+2^6;y=2^60;x-y
ans=
0
Ejercicio 2 propuesto del tema 1. 
f=@(x) (exp(x)-1).^2+(1./sqrt(1+x.^2)-1).^2;
k=-1:-1:-17;
h=10.^(k);
v=(f(1+h)-f(1))./h;
format long
disp([h' v'])
%h a partir del valor k=-16 es cero
%La función para h pequeño tiende a cero y
%se produce también cancelación en el segundo
%sumando.
Ejemplo. Se sabe que ${e^x} = \sum\limits_{n = 0}^\infty {{{{x^n}} \over {n!}}} $. Calcula una aproximación de $e^{-40}$ con los 100 primeros términos de la serie. 
Si $x< 0$ los términos de la serie cambian de signo y si $|x|$ es grande, el valor de los sumandos puede devolver un valor pequeño cuando los sumandos sean muy grandes. En algún momento estaremos con un error de cancelación cuando sumemos "el siguiente" término. la manera de arreglar el problema es usar el hecho de que
${e^{ - x}} = {1 \over {{e^x}}}$. Calcula $e^{-40}$ teniendo esto en cuenta y utilizando la aproximación que darán los 100 primeros sumandos.
x=40; %Inverso del número a calcular
suma=1;
p=1;
for k=1:99
p=p*(x/k);
suma=suma+p;
end
1/suma
x=-40; %Sin considerar el inverso
suma=1;
p=1;
for k=1:99
p=p*(x/k);
suma=suma+p;
end
suma
Ejercicio 5 propuesto del tema 1. 
Apartado a
f=@(x) 1./(1+2*x)-(1-x)./(1+x);
%Se realiza la suma para evitar la cancelación
g=@(x) 2*x.^2./((1+2*x).*(1+x));
k=-1:-1:-17;
h=10.^k;
f1=f(h);
g1=g(h);
format long
disp([h' f1' g1'])
Apartado b
f=@(x) (1-cos(x))./x;
%Se multiplica y divide por (1+cos(x))
g=@(x) sin(x).^2./(x.*(1+cos(x)));
k=-1:-1:-17;
h=10.^k;
f1=f(h);
g1=g(h);
format long
disp([h' f1' g1'])
Apartado c
f=@(x) sqrt(x+1./x)-sqrt(x-1./x);
%Se multiplica y divide por el conjugado
g=@(x) 2*x./((sqrt(x+1./x)+sqrt(x-1./x)));
k=-1:-1:-25;
h=10.^k;
f1=f(1+h);
g1=g(1+h);
format long
disp([h' f1' g1'])
Error por desbordamiento
Con frecuencia una operación aritmética con dos números válidos da como resultado un número tan grande o tan pequeño que la computadora no puede manejarlo; como consecuencia se produce un overflow o un underflow, respectivamente.
Propagacion de errores
Para este análisis tengamos en cuenta que si
$$x = {\left( { - 1} \right)^s}× {2^{{e_x}}} × 1.f\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 < {e_x} < 1024$$ de acuerdo a las reglas de redondeo se tiene que $$\left| {x - fl\left( x \right)} \right| \le {2^{{e_x}}} \cdot {2^{ - 53}} \Rightarrow {{\left| {x - fl\left( x \right)} \right|} \over {\left| x \right|}} \le {2^{ - 53}}$$Al valor $2^{-53}$ se le llama épsilon de la máquina, que denotaremos por ${\varepsilon _M}$ y nos da una cota superior del error relativo debido a la expresión en formato punto flotante de un número.
Análisis del error de propagación
Si $\otimes$ es una operáción aritmética el cálculo sigue el siguiente proceso:
$$fl\left( {x \otimes y} \right) = fl\left( {fl\left( x \right) \otimes fl\left( y \right)} \right)$$- Almacena los números $x$ e $y$ en coma flotante.
- Después realiza la operación con los números obtenidos.
- Finalmente da el resultado en punto flotante.
Errores de redondeo de la suma
Vamos a analizar el error originado a la hora de realizar la operación en punto flotante y representar los números en punto flotante. Denotemos por ${\varepsilon _x}$, el error relativo entre $x$ y su representación en coma flotante $fl(x)$ $${\varepsilon _x} = {{x - fl\left( x \right)} \over x} \,\,\,\,\,\,\,\left| {{\varepsilon _x}} \right| \le {\varepsilon _M}$$ $$fl\left( x \right) = x\left( {1 + {\varepsilon _x}} \right)\,\,\,\,\,\,\,\left| {{\varepsilon _x}} \right| \le {\varepsilon _M}$$
Dados $x$, $y$ se tiene que: $$fl\left( x \right) = x\left( {1 + {\varepsilon _x}} \right)\,\,\,\,\,\,\,\left| {{\varepsilon _x}} \right| \le {\varepsilon _M}$$ $$fl\left( y \right) = y\left( {1 + {\varepsilon _y}} \right)\,\,\,\,\,\,\,\left| {{\varepsilon _y}} \right| \le {\varepsilon _M}$$
y si $z=x+y$ entonces $$fl\left( z \right) = \left( {x\left( {1 + {\varepsilon _x}} \right) + y\left( {1 + {\varepsilon _y}} \right)} \right)\left( {1 + {\varepsilon _z}} \right)$$
Se puede probar que el error relativo cometido al realizar la suma está acotado por: $$E \le {{\left| x \right| + \left| y \right|} \over {\left| {x + y} \right|}}\left( {2 + {\varepsilon _M}} \right){\varepsilon _M}$$
- si signo(x)=signo(y), entonces $\varepsilon _z \le (2+ \varepsilon _M) \varepsilon _M$
- si signo(x)=signo(y), entonces $\varepsilon _z \le {{\left| x \right| + \left| y \right|} \over {\left( {\left| x \right| - \left| y \right|} \right)}}\left( {2 + {\varepsilon _M}} \right){\varepsilon _M}$
Observamos que el error originado por la operación en sí y por la expresión inexacta de los sumandos será pequeño en cuanto $x+y$ no sea pequeño. Sin embargo, si los números a sumar son aproximadamente iguales en magnitud, pero de signos opuestos, el error relativo es muy grande. Esta situación, conocida como cancelación de dígitos significativos, debe ser evitada tanto como sea posible.
Veamos cómo obtener la expresión anterior.
Dado que $$fl\left( x+y \right) = \left( {x + x{\varepsilon _x} + y + y{\varepsilon _y}} \right)\left( {1 + {\varepsilon _z}} \right)$$ el error relativo $$E = \left| {{{z - fl\left( z \right)} \over z}} \right| = {{\left| {x + y - \left( {x + x{\varepsilon _x} + y + y{\varepsilon _y}} \right)\left( {1 + {\varepsilon _z}} \right)} \right|} \over {\left| {x + y} \right|}} $$Análogamente puede demostrarse las acotaciones de errores relativos para las siguientes operaciones:
- Multiplicación: Si $z = fl\left( x \right) \cdot fl\left( y \right)$ $$E = {{\left| {x \cdot y - fl\left( z \right)} \right|} \over {\left| {x \cdot y} \right|}} \le \left( {3 + 3{\varepsilon _M} + \varepsilon _M^2} \right){\varepsilon _M}$$
- División: $z = fl\left( x \right)/fl\left( y \right)$ $$E = {{\left| {{x \over y} - fl\left( z \right)} \right|} \over {\left| {{x \over y}} \right|}} \le {{3 + {\varepsilon _M}} \over {1 - {\varepsilon _M}}}{\varepsilon _M}$$
Octave online
Octave es una alternativa a Matlab con un aspecto y unos comandos y sintasis similares. Se trata de un lenguaje interpretado de alto nivel. Lo puedes descargar desde su página oficial completamente gratis. Aquí tienes el enlace de descarga.
Pero además, puedes utilizar una versión en línea desde tu móvil en el caso de que no tengas a mano tu ordenador. Esta versión la tienes aquí: Octave online.
Resolución aproximada de
ecuaciones escalares no lineales
Introducción
Imaginemos que consideramos la siguiente ecuación obtenida a partir de la segunda ley de Newton que permite obtener la velocidad de un paracaidista, $$v = {{g \cdot m} \over c}\left( {1 - {e^{ - {c \over m}t}}} \right)$$ donde la velocidad $v$ depende el tiempo, $t$ es el tiempo y es la variable independiente, $g$ es la constante de gravitación y $c$ el coeficiente de resistencia y $m$ la masa del paracaidista. ¿Cómo se podría obtener el coeficiente de resistencia del paracaidista con una masa dada, para alcanzar una velocidad determinada en un periodo establecido?
Si consideramos $$f\left( c \right) = {{g \cdot m} \over c}\left( {1 - {e^{ - {c \over m}t}}} \right) - v$$ el problema se corresponde con calcular el valor de $c$ de forma que $f(c)=0$. Vamos a ver en este capítulo cómo obtener el valor de la raíz o solucion de la función $f$.
En la mayoría de los casos, no será posible determinar la solución exacta de una ecuación de la forma $f(x)=0$ siendo $f$ una función real de variable real y se aplicará un algoritmo para determinar, en un número finito de pasos, un valor aproximado. Estos métodos de aproximación que, en general, son iterativos nos conducen a una solución a través de una sucesión $x_0, x_1, ..., x_k,...$ que converge al valor $x$ que es solución de la ecuación $f(x)=0$. Analizaremos también los problemas de convergencia y error que pueden presentarse.
Convergencia de un algoritmo
Se dice que un algoritmo converge globalmente, si la sucesión generada es convergente hacia una solución de la ecuación cualquiera que sea el punto inicial $x_0$ que tomemos. Cuando la solución converge hacia la solución únicamente si el punto $x_0$ pertenece a un cierto entorno de $x_0$, la convergencia es local.
No siempre es mejor considerar un algoritmo que converja globalmente, a veces, un algoritmo que sea localmente convergente, puede tener una "velocidad de convergencia" mayor si bien este tipo de algoritmos plantean la dificultad de cómo elegir el intervalo adecuado donde elegir $x_0$.
El método de aproximaciones sucesivas, que consiste en partir de un punto $x_0$ y calcular los demás términos de la sucesión $x_n$ de la forma $x_n+1=g(x_n)$, tiene una convergencia más lenta que el método de Newton que veremos en este capítulo y converge localmente.
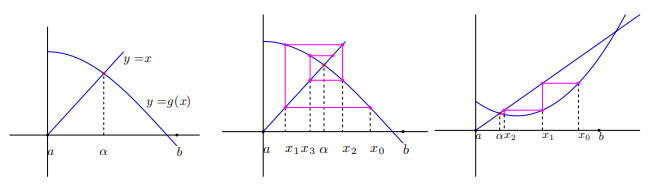
Se distinguen distintos tipos de convergencia que pasamos a definir.
Dada una sucesión de números reales, $\left\{ {x _k} \right\}_{k = 1}^\infty $, convergente hacia un punto $\overline x$, se dice que el orden o velocidad de convergencia es $p$, con $p \ge 1$ si existe una constante $C_p \ge 0$ tal que: $$\left| {{x_{k + 1}} - \overline x } \right| \le {C_p}{\left| {{x_k} - \overline x \,} \right|^p}\,\,\,\,\forall k \ge k_0 para algún k_0 entero$$
- si $p$=1 y $C_p< 1$, la convergencia es lineal. Si $C_p \ge 1$, la convergencia es sublineal.
- si $p$=2, la convergencia es cuadrática.
- si $p$=3, la convergencia es cúbica.
Se dice que la sucesión converge superlinealmente, si existe una sucesión $\left\{ {{\varepsilon _k}} \right\}_{k = 1}^\infty $ convergente a 0 tal que $$\left| {{x_{k + 1}} - \bar x} \right| \le {\varepsilon _k}\left| {{x_k} - \bar x{\mkern 1mu} } \right|\,\,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \forall k \ge 0$$
Observa que si la sucesión tiene una velocidad de convergencia $p$ mayor que 1 entonces converge superlinealmente.
Bastaría tomar $${\varepsilon _k} = {C_p}{\left| {{x_k} - \bar x{\mkern 1mu} } \right|^{p - 1}}\,\,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \forall k \ge 0$$
Si $x_k$ converge superlinealmente a ${\bar x}$ entonces $$\mathop {\lim }\limits_{k \to \infty } {{\left| {{x_{k + 1}} - {x_k}{\mkern 1mu} } \right|} \over {\left| {{x_k} - \bar x{\mkern 1mu} } \right|}} = 1$$
Este resultado permite determinar un test de parada de las iteraciones cuando la convergencia es superlineal. Una vez establecida la precisión que se quiere alcanzar, $\varepsilon > 0$, el test será: $$\left| {{x_{k + 1}} - {x_k}} \right| < \varepsilon$$ se compara así dos iteraciones consecutivas y se mira la coincidencia de dígitos que se considere (fijado por el valor de $\epsilon$).
Método de Newton
Este método aproxima la solución de la ecuación $$f(x)=0$$ mediante una sucesión $x_k$ contruida a partir de un valor inicial $x_0$ a partir de la siguiente expresión iterativa: $$x_{k+1} = x_k − \frac{f(x_k )}{ f'(x_k )}$$ La idea es, una vez obtenido $x_k$, obtener $x_{k+1}$ utilizando una aproximación lineal de $f(x)$ en el punto $x_k$. Se utiliza para ello la derivada $f$ en dicho punto: $$f(x) ≈ f(x_k )+f'(x_k)(x−x_k)$$ y se toma $x_{k+1}$ como la solución de la ecuación lineal $$f(x_k ) + f'(x _k )(x − x_k ) = 0$$
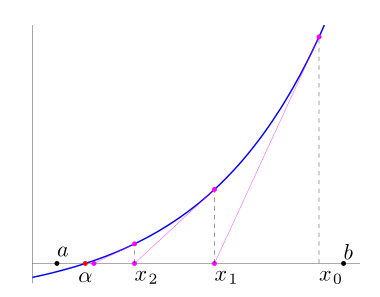
En la escena que se presenta a continuación, se muestra gráficamente la forma de proceder en el Método de Newton.
Tomando el punto inicial $x_0$ cercano a la solución, bajo ciertas condiciones sobre la función $f$, el método de Newton es convergente con orden de convergencia cuadrático (de orden 2).
Recordemos el siguiente teorema:
Si $f$ es una función continua en $[a,b]$ de manera que $f(a)f(b) < 0$, entonces podemos asegurar que existe al menos un cero de la función en el intervalo [a,b].
El hecho de que sepamos que la función $f$ tiene un cero, no significa que sea único. Si añadimos condiciones adicionales, como por ejemplo la monotonía estrica, sí se podría garantizar que la solución es única.
Ejemplo. Busquemos la solución de la ecuación no lineal $$x-cos(x)=0$$
Tomamos el intervalo $[0,1]$ como el intervalo $[a,b]$ donde $f(a)f(b)$<$0$. Como punto $x_0$, consideramos el punto medio del intervalo $[0,1]$.
$x_0=0.5$
$x_1=x_0-\frac{x_0-cos(x_0)}{1+sen(x_0)}$ 0.755222417105636
$x_2=x_1-\frac{x_1-cos(x_1)}{1+sen(x_1)}$ 0.739141666149879
$x_3=x_2-\frac{x_2-cos(x_2)}{1+sen(x_2)}$ 0.739085133920807
$x_4=x_3-\frac{x_3-cos(x_3)}{1+sen(x_3)}$ 0.739085133215161
$x_5=x_3-\frac{x_3-cos(x_3)}{1+sen(x_3)}$ 0.739085133215161
El código Matlab a utilizar para encontrar la solución se muestra a continuación.
x=0.5
x=x-(x-cos(x))/(1+sin(x))
%A partir de la cuarta iteración se
%estabiliza el resultado
Observad que en este caso, se duplica, aproximadamentemente, la cantidad de decimales de cada iteracion (convergencia cuadrática).
Veamos a continuación como ejemplos algunos de los ejercicios propuestos.
Ejercicio 1 propuesto del tema 2. 
Apartado d
df=inline('exp(x)-log(2)*2^-x-2*sin(x)')
%Tomamos [1,2]
%Aplicamos el Método de Newton
x=1.5
x=x-f(x)/df(x)
%repetimos iteraciones hasta conseguir
%16 decimales
| $x_0$ | 1.500000000000000 | ||
| $x_1$ | 1.956489721124211 | $x_5$ | 1.829383601933849 |
| $x_2$ | 1.841533061042061 | $x_6$ | 1.829383601933849 |
| $x_3$ | 1.829506013203651 | ||
| $x_4$ | 1.829383614494166 |
Para calcular la diferencia entre dos iteraciones se podría utilizar el siguiente código Matlab:
df=inline('exp(x)-2^-x*log(2)-2*sin(x)')
x=1.5
x1=x-f(x)/df(x),error=abs(x-x1),x=x1;
df=inline('exp(x)+2^-x*log(2)-2*sin(x)')
k=1; x(k)=1.5
x(k+1)=x(k)-f(x(k))/df(x(k)),error=abs(x(k)-x(k+1)),k=k+1;
Ejercicio 2 propuesto del tema 2. 
%polyder deriva el polinomio
dp=polyder(p)
%polyval(p,a) evalúa el polinomio en a
%método de Newton
%intervalo [-4,-3]
polyval(p,-4);polyval(p,-3)
x=-3.25
x=x-polyval(p,x)/polyval(dp,x)
%repetimos iteracion, sol=-3.195823345445647
Si se repite con $x_0=1$ se puede observar que oscila entre negativo y positivo, no converge. Esto ocurre porque el método de Newton converge localmente.
Método de Bisección
Una forma sencilla de aproximar el cero de la función es dividir el intervalo en dos y elegir el subintervalo en el que se sigue produciendo el cambio de signo. Repitiendo este proceso se puede llegar a conseguir una aproximación de la solución de $f(x) = 0$ tan precisa como se desee.

Método de Newton combinado con la bisección
Supongamos que $f(a)f(b) < 0$. Se considera $a$ , $b$ y $x_0=\frac{a+b}{2}$.
En cada iteración se busca una nueva aproximación $x'$ y se actualizan $a$ y $b$ como se indica a continuación:
- Si $x'=x_0-\frac{f(x_0)}{f'(x_0}$ está en $[a,b]$ se acepta, en caso contrario se utiliza bisección, es decir, $x'=\frac{a+b}{2}$
- Se realiza $a'=x'$, $b'=b$ o $a'=a$, $b'=x'$, de manera que $f(a')f(b') < 0$
No se aplicará el método de Newton cuando el denominador $f'(x_k)$ sea muy pequeño (overflow), o mejor, cuando el cociente $\frac{f(x_k)}{f'(x_k)}$ sea muy grande. Es decir,no utilizaremos el método de Newton cuando $$|\frac{f(x_k)}{f'(x_k)}| < \frac{1}{\epsilon_M}$$ Esta última condición se implementa de la forma siguiente: $$|{f'(x_k)}| > {\epsilon_M} |{f(x_k)}|$$
Como tests de parada en las iteraciones, se considerarán:
- que la diferencia entre dos iteraciones consecutivas sea menor que un cierto valor $\epsilon$ $$\left| {{x_{k + 1}} - {x_k}} \right| < \varepsilon \,\,\,\,\text{error absoluto}$$ $$\left| {{x_{k + 1}} - {x_k}} \right| < \varepsilon |{x_{k+1}}| \,\,\,\,\text{error relativo}$$ combinando estos dos errores $$\left| {{x_{k + 1}} - {x_k}} \right| < \varepsilon \max \left\{ {1,\left| {{x_{k + 1}}} \right|} \right\}$$
- dado que se busca $f(x)=0$ se parará cuando $f(x_{k+1})$ sea pequeño, lo que comprobaremos con el test $$|f(x_{k+1})| < \epsilon_f$$ Para funciones sencillas un valor habitual es $$\varepsilon_f = \varepsilon _M^{3/4}$$
En el siguiente enlace puedes ver resumido el algoritmo.
Presentamos a continuación el algoritmo aplicado a un ejemplo:
Ejercicio 1d propuesto del tema 2.  . Encontrar la raiz de $$e^x+2^{-x}+2cos(x)-6=0$$ en $[1,2]$.
. Encontrar la raiz de $$e^x+2^{-x}+2cos(x)-6=0$$ en $[1,2]$.
f=inline('exp(x)+2^-x+2*cos(x)-6')
df=inline('exp(x)-log(2)*2^-1-2*sin(x)')
f(1)*f(2)
em=eps/2
a=1;b=2;fa=f(a);fb=f(b);x=(a+b)/2;fx=f(x);
[fa fx fb]
ans =
-1.701113559804675 -1.023283135733256 0.806762425836365
Si $fa \cdot fx < 0$ se considera $[a,x]$, en caso contrario se considera $[x,b]$.
Iteración 1
a=x;fa=fx;m=df(x);
if abs(m)>em*abs(fx),x=x-fx/m;[a x b],end
fx=f(x); [fa fx fb]
ans =
1.500000000000000 1.956489721124211 2.000000000000000
ans =
-1.023283135733256 0.579701373274924 0.806762425836365
Iteración 2
if abs(m)>em*abs(fx),x=x-fx/m,end
fx=f(x);[fa fx fb]
ans =
1.500000000000000 1.841533061042061 1.956489721124211
ans =
-1.023283135733256 0.050340951614865 0.579701373274924
Iteración 3
if abs(m)>em*abs(fx),x=x-fx/m,end
fx=f(x);[a x b],[fa fx fb]
ans =
1.500000000000000 1.829506013203651 1.841533061042061
ans =
-1.023283135733256 0.000502121322591 0.050340951614865
Iteración 4
if abs(m)>em*abs(fx),x=x-fx/m,end
fx=f(x);[a x b],[fa fx fb]
ans =
1.500000000000000 1.829383614494166 1.829506013203651
ans =
-1.023283135733256 0.000000051516139 0.000502121322591
Iteración 5
if abs(m)>em*abs(fx),x=x-fx/m,end
fx=f(x);[a x b],[fa fx fb]
ans =
1.500000000000000 1.829383601933849 1.829383614494166
ans =
-1.023283135733256 0.000000000000001 0.000000051516139
Ejercicio 1d propuesto del tema 2.  . Encontrar la raiz de $$e^x+2^{-x}+2cos(x)-6=0$$ que se encuentra entre $[-3,-2]$.
. Encontrar la raiz de $$e^x+2^{-x}+2cos(x)-6=0$$ que se encuentra entre $[-3,-2]$.
df=inline('exp(x)-log(2)*2^(-x)-2*sin(x)')
f(-3)*f(-2)
a=-3;fa=f(a);b=-2;fb=f(b);x=(a+b)/2;fx=f(x),
[a x b],[f(a) f(x) f(b)]
-3.000000000000000 -2.500000000000000 -2.000000000000000 ans =
0.069802075166974 -1.863347982977588 -2.696958389857672
Iteración 1
if abs(dfx)>em*abs(fx),x=x-fx/dfx;if a$<$=x & b$>$=x, disp('Se aplica Newton'),
[a x b],fx=f(x);end,end
%Si no está en [a,b] o no se
%cumple abs(dfx)>em*abs(fx)
%aplicamos bisección
x=(a+b)/2;fx=f(x);[a x b],[fa fx fb]
-3.000000000000000 -2.750000000000000 -2.500000000000000
ans =
0.069802075166974 -1.057505574028503 -1.863347982977588
Iteración 2 Bisección
-3.000000000000000 -2.875000000000000 -2.750000000000000
ans =
0.069802075166974 -0.536899807501486 -1.057505574028503
Iteración 3 Newton
-3.000000000000000 -2.994267548648236 -2.875000000000000
ans =
0.069802075166974 0.040014356224199 -0.536899807501486
Iteración 4 Newton
-2.994267548648236 -2.986542066999646 -2.875000000000000
ans =
0.040014356224199 0.000174552940576 -0.536899807501486
Iteración 5 Newton
-2.986542066999646 -2.986508070038639 -2.875000000000000
ans =
0.000174552940576 0.000000003371666 -0.536899807501486
Iteración 6: Newton
-2.986508070038639 -2.986508069381928 -2.875000000000000
ans =
0.000000003371666 0 -0.536899807501486
El método de Newton tiene el problema de que podría darse “overflow” si se divide por un número muy pequeño, o converger a otra raíz (no a la raíz que se busca) o incluso no converger. Además, al requerir la derivada de la función podría ser difícil de obtener en el caso de ciertas funciones como las definidas por integrales o por series infinitas por ejemplo.
Método de la secante
Iniciado con dos aproximaciones iniciales $x_o$ y $x_1$, en el paso $k+1$, $x_{k+1}$ se calcula usando $x_k$ y $x_{k-1}$ como la intersección con el eje X de la recta secante, que pasa por los puntos $(x_{k-1}, f(x_{k-1})$ y $(x_{k}, f(x_{k})$
La ecuación de la recta secante es $$y = f\left( {{x_k}} \right) + {m_k}\left( {x - {x_k}} \right)\,\,\,\,\,\,\,\,\,\,\,\,{m_k} = {{f\left( {{x_k}} \right) - f\left( {{x_{k - 1}}} \right)} \over {{x_k} - {x_{k - 1}}}}$$
El método proporciona $x_{k+1}$ como solución de $$0 = f\left( {{x_k}} \right) + {m_k}\left( {x - {x_k}} \right)$$ Es decir, $${x_{k + 1}} = {x_k} - {{f\left( {{x_k}} \right)} \over {{m_k}}}\,\,\,\,\,\,\,\,\,\,\,\,{m_k} = {{f\left( {{x_k}} \right) - f\left( {{x_{k - 1}}} \right)} \over {{x_k} - {x_{k - 1}}}}$$
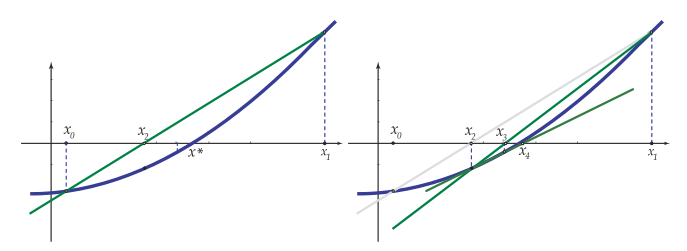
Método de la secante-bisección
De la misma forma que el método de Newton, resulta muy conveniente combinar programar este método combinado con el método de la bisección
Se partirá de un intervalo $[a,b]$ donde $f(a)f(b)< 0$. Se toma $x_0=a$ y $x_1=b$.
En cada iteración, se parte de un intervalo $[a,b]$ y se busca una nueva aproximación $x'$ actualizando de nuevo $a$ y $b$ como se indica a continuación:
- Si $x'=x_1-\frac{f(x_1)}{m_0}$ está en $[a,b]$ se acepta, en caso contrario se utiliza bisección, es decir, $x'=\frac{a+b}{2}$
- Se realiza $a'=x'$, $b'=b$ o $a'=a$, $b'=x'$, de manera que $f(a')f(b') < 0$
Tampoco se aplicará el método de la secante cuando el denominador $m_k$ sea muy pequeño. Esta última condición se implementa de la forma siguiente: $$|{m_k}| > {\epsilon_M} |{f(x_k)}|$$
Los test de parada a utilizar son los mismos que en el caso del método Newton-Bisección.
Ejercicio 10 propuesto del tema 2. 
f=inline('erf(x)-0.5')
f(0)*f(1)
a=0;b=1;fa=f(a);fb=f(b);x0=a;fx0=fa;x1=b;fx1=fb;
m=(fx1-fx0)/(x1-x0);
if abs(m)>em*abs(fx1);x=x1-fx1/m;end
[a x b],[fa fx fb]
%Se comprueba que está en [a,b]
Iteración 1:
0 0.593330401707401 1.000000000000000
ans =
-0.500000000000000 0.098584503929305 0.342700792949715
Iteración 2:
0 0.429099981968989 0.593330401707401
ans =
-0.500000000000000 -0.043957753989566 0.098584503929305
Iteración 3:
0.429099981968989 0.479746018406641 0.593330401707401
ans =
-0.043957753989566 0.002522030582461 0.098584503929305
Iteración 4:
0.429099981968989 0.476997923639157 0.479746018406641
ans =
-0.043957753989566 0.000055407570768 0.002522030582461
Iteración 5:
0.476936193389100 0.476936276206905 0.476997923639157
ans =
Iteración 6:
ans =
1.0e-04 * -0.000744351095761 0.000000021886937 0.554075707681623
Iteración 7:
0.476936193389100 0.476936276204470 0.476936276206905
ans =
1.0e-07 * -0.744351095760543 0 0.000021886936707
Ejercicio 12 propuesto del tema 2. 
%f(x)=det(A(x)+2I)
f=inline('det([x+2 2 -3 5 0 x^2;1 3 1 1 1 1;0 x x+2 0 5 -2;1 -1 1 1 2*x 0;1 0 1 0 (x^2)+2 -2;0 0 1 0 cos(x) -x+2])')
%Buscamos cambios de signo
% f(0)$<$0
% f(1)$<$0
% f(2)$>$0
% f(3)$<$0
% f(4)$<$0
% f(5)$<$0
% f(-1)$<$0
% f(-2)$<$0
Aplicamos el método de la secante dada la dificultad de calcular la derivada.
a=1;b=2;fa=f(a);fb=f(b);x0=a;x1=b;fx0=fa;fx1=fb;
m=(fx1-fx0)/(x1-x0);
if abs(m)>em*abs(fx1),x=x1-fx1/m;end
[a x b],fx=f(x);[fa fx fb]
%Hay que comprobar que el punto
%quede dentro del intervalo
%Se itera hasta que converja
ans =
1.182136884006676
Cálculo de las raíces de un polinomio
En este apartado, nos ocuparemos de encontrar todas las soluciones (reales y complejas) de un polinomio, es decir, resolveremos todas las soluciones de $${a_o} + {a_1}x + {a_2}{x^2} + ... + {a_n}{x^n} = 0$$
- Teorema Fundamental del Álgebra: Un polinomio de grado $n$ tiene exactamente $n$ raíces en el conjunto de los números complejos, donde cada una de ellas debe contarse con su multiplicidad.
- Si un polinomio tiene coeficientes reales, siempre que tenga una raiz compleja no real, también tendrá su conjugada.
Aunque inicialmente se había descrito el método de Newton para calcular las soluciones de una ecuación $f(x)=0$ con $f$ función real de variable real, el método también es válido para encontrar soluciones de funciones complejas. Además, la derivada de un polinomio es fácilmente calculable por lo que el método de Newton resulta adecuado para calcular las raíces de un polinomio.
Sin embargo, nos planteamos a la hora de calcular todas las raíces del polinomio, si una vez obtenida una raíz, $\alpha$, y querer encontrar otra, ¿cómo evitar que el método de Newton vuelva a converger a la raíz ya calculada?
Una primera idea sería elegir otro punto de inicio, sin embargo, esto no garantizaría que el método deba converger a otra raíz.
Otra posibilidad, podría ser considerar el polinomio resultado de dividir $p(x)$ entre $x-\alpha$ y aplicar el método de Newton a este nuevo polinomio. Este método, conocico como deflacción, presenta también problemas:
- La operación de división conlleva errores de redondeo.
- El método de Newton nos devuelve una aproximación de la raíz exacta, $\alpha *$ por lo que el cociente $\frac{p(x)}{x-\alpha}$ no coincide con $\frac{p(x)}{x-\alpha *}$ y, en consecuencia, no tienen porqué tener las mismas raíces.
Dado que el hecho de que dos polinomios sean próximos (tengan coeficientes muy próximos) no implica que tengan las mismas raíces, el método alternativo a utilizar es el Método de Maehly.
La idea de este método es, una vez calculadas las raíces $$\left\{ {{\alpha _1},{\alpha _2},...,{\alpha _m}} \right\}$$ del polinomio $p(x)$, aplicar el método de Newton al polinomio $${f_m} = {{p\left( x \right)} \over {\left( {x - {\alpha _1}} \right)\left( {x - {\alpha _2}} \right)...\left( {x - {\alpha _m}} \right)}}$$ Nota: Sin hacer la división
Se puede ver que $${{{f_m}\left( x \right)} \over {f{'_m}\left( x \right)}} = {{p\left( x \right)} \over {p'\left( x \right) - p\left( x \right)\sum\limits_{j = 1}^m {{1 \over {x - {\alpha _j}}}} }}$$
Puedes descargar el fichero itraiz.m que realiza una iteración del método de Maehly.
Hay que tener en cuenta que
- En la primera iteración el algoritmo se reduce a aplicar el método de Newton al polinomio: $$\begin{aligned} & {x_o} \in \mathbb C \\ & x_{k + 1} = {x_k} - \frac{p(x_k)} {p'(x_k)} \,\,\,\,\,\, k \ge 0 \end{aligned}$$
- Si los coeficientes del polinomio son todos reales y $x_0$ es real, la sucesion ${x_k}$ será de números reales y no podrá converger a una raíz compleja. Por lo tanto, deberá tomarse $x_0$ complejo si se quiere encontrar una raíz compleja.
El método de Newton converge cuadráticamente hacia una raíz $\overline x$ si $p'(\overline x)\ne0$. Si se observa que los valores de $x_k$ convergen pero lentamente, puede deberse a que se está aproximando a una raíz múltiple o hay raíces muy próximas. En este caso se aplica el método de Newton a la derivada del polinomio comenzando en el último punto $x_k$ calculado en las iteraciones de $p$.
Si la convergencia siguiera siendo lenta, entonces se aplicaría el método de Newton a la segunda derivada. Si calculamos una raíz $\alpha$ de $p'(x)$ (o de derivadas sucesivas de p) y observamos que $$\left| {p\left( \alpha \right)} \right| \gg \left| {p'\left( \alpha \right)} \right|$$ entonces debemos concluir que $\alpha$ no es raíz de $p$. lo que ocurre es que $p$ posee dos o más raíces muy próximas. En caso contrario, tendremos que $\alpha$ es una raíz doble de $p$ (o de multiplicidad $j+1$ si $$p\left( \alpha \right),\,\,p'\left( \alpha \right)...{p^{(j}}\left( \alpha \right)$$ toman valores muy pequeños.
En el caso de que haya raíces próximas entonces la convergencia será lenta y, en general, no podremos obtener una precisión alta en la solución.
- Si el polinomio tiene coeficientes reales y $\alpha=a+bi$ es una raiz compleja entonces su conjugada $\overline \alpha = a - bi$ también es raíz del polinomio. Además, si $\alpha$ tuviera multiplicidad $m$, entonces $\overline \alpha$ tendría la misma multiplicidad.
Ejercicio 13 apartado f propuesto del tema 2. 
dp=polyder(p)
v=[]
x=i
format long
x=itraiz(p,dp,v,x)
%Se hacen iteraciones hasta encontrar x
-1.056847723228969 + 0.262522264027478i
polyval(p,x)
x=i;x=itraiz (p,dp,v,x)
-0.059269229873907 + 2.202319797999819i
polyval(p,x)
x=i;x=itraiz (p,dp,v,x)
2.063556841734012
polyval(p,x)
Se obtienen así las 7 raíces
-1.056847723228969 + 0.262522264027478i
-1.056847723228969 - 0.262522264027478i
-1.540661467764130 + 1.474052474547216i
-1.540661467764130 - 1.474052474547216i
-0.059269229873907 + 2.202319797999819i
-0.059269229873907 - 2.202319797999819i
2.063556841734012 + 0.000000000000000i
Ejercicio 13 apartado h propuesto del tema 2. 
Octave online
Octave es una alternativa a Matlab con un aspecto y unos comandos y sintasis similares. Se trata de un lenguaje interpretado de alto nivel. Lo puedes descargar desde su página oficial completamente gratis. Aquí tienes el enlace de descarga.
Pero además, puedes utilizar una versión en línea desde tu móvil en el caso de que no tengas a mano tu ordenador. Esta versión la tienes aquí: Octave online.
Aproximación de
funciones de una
variable por polinomios
Introducción
A menudo se dispone de una tabla de datos obtenida por muestreo o experimentación y se supone que los datos corresponden a los valores de una función $f$ desconocida o, aunque sea conocida, se precisa cambiarla por una más sencilla de calcular. Un caso particular de ajuste de curvas consiste en construir un polinomio $P(x)$ que pase por los puntos de esta tabla de valores.
En este capítulo mostraremos dos técnicas para aproximar la función por un polinomio: la interpolación y la aproximación por mínimos cuadrados. Dentro de la interpolación veremos la interpolación de Lagrange y la de Hermite.
Interpolación de Lagrange
 Joseph Louis Lagrange (1736-1813) fue uno de los más grandes matemáticos de su tiempo. Nació en Italia pero se
nacionalizó Francés. Hizo grandes contribuciones en todos los campos de la matemática y también en mecánica. Su obra principal es la “Mécanique analytique”(1788). En esta obra de cuatro volúmenes, se ofrece el tratamiento más
completo de la mecánica clásica desde Newton y sirvió de base para el desarrollo de la física matemática en el siglo
XIX. de una función $f$ definida en $[a,b]$ es el polinomio de grado menor o igual a $n$ que cumple $p(x_i)=f(x_i)$ para cada i entre 0 y n. A los puntos ${x_0,x_1,...,x_n}$ se les llama nodos de interpolación.
Joseph Louis Lagrange (1736-1813) fue uno de los más grandes matemáticos de su tiempo. Nació en Italia pero se
nacionalizó Francés. Hizo grandes contribuciones en todos los campos de la matemática y también en mecánica. Su obra principal es la “Mécanique analytique”(1788). En esta obra de cuatro volúmenes, se ofrece el tratamiento más
completo de la mecánica clásica desde Newton y sirvió de base para el desarrollo de la física matemática en el siglo
XIX. de una función $f$ definida en $[a,b]$ es el polinomio de grado menor o igual a $n$ que cumple $p(x_i)=f(x_i)$ para cada i entre 0 y n. A los puntos ${x_0,x_1,...,x_n}$ se les llama nodos de interpolación.
Ejercicio 1 propuesto del tema 3.  Calcular los polinomios base.
Calcular los polinomios base.
Aunque la fórmula del teorema anterior posee un interés teórico, no es la forma eficiente de calcular el polinomio interpolador. Un método sencillo y más rápido es el siguiente. Como se quiere calcular $p(x) = {a_o} + {a_1}x + ... + {a_n}{x^n}$ de forma que $p({x_i}) = f\left( {{x_i}} \right)$, se tendrá que cumplir que: $$\begin{pmatrix} 1& {{x_o}}&{x_o^2}&{...}&{x_o^n}\\ 1&{{x_1}}&{x_o^2}&{...}&{x_1^n}\\ 1&{{x_2}}&{x_o^2}&{...}&{x_2^n}\\ {...}&{...}&{...}&{...}&{...}\\ 1&{{x_n}}&{x_o^2}&{...}&{x_n^n} \end{pmatrix} \begin{pmatrix} {a_0} \\ {a_1}\\ {a_2}\\ {...}\\ {a_n} \end{pmatrix} = \begin{pmatrix} {f\left( {{x_o}} \right)}\\ {f\left( {{x_o}} \right)}\\ {f\left( {{x_o}} \right)}\\ {...}\\ {f\left( {{x_n}} \right)} \end{pmatrix}$$
El método consiste en construir la matriz $A$ de orden $(n+1)x(n+1)$, el vector b de $\mathbb{R}^n$ y resolver el sistema $Aa=b$, donde $a$ es el vector de los coeficientes. Dado que el problema de interpolación de Lagrange tiene una única solución, la matriz $A$ es invertible.
Ejercicio 1 propuesto del tema 3.  Calcular el polinomio interpolador.
Calcular el polinomio interpolador.
A=ones(n+1,1);t=A;
for k=1:n
t=t.*x;
A=[t,A];
end
a=A\b
%Comprobación
polyval(a,x)
Ejercicio 1 propuesto del tema 3.  . Calcular una cota del error.
. Calcular una cota del error.
q=poly([-1 1 2]);dq=polyder(q);
r=roots(dq);v=polyval(q,r)
max(abs(v))
%2.112611790922380
La elección de nodos que permite minimizar el valor de \[\mathop {\max }\limits_{x \in \left[ {a,b} \right]} \left| {\prod\limits_{j = 0}^n {\left( {x - {x_j}} \right)} } \right|\] se consigue con los puntos de Chebyshev.
Nodos de Chebyshev. Los nodos de Chebyschev  Pafnuti Lvóvich Tchebyschev (1821 - 1894). El más prominente miembro de la escuela de matemáticas de St. Petersburg. Hizo
investigaciones en Mecanismos, Teoría de la Aproximación de Funciones, Teoría de los Números, Teoría de Probabilidades y
Teoría de Integración. Sin embargo, escribió acerca de muchos otros temas: formas cuadráticas, construcción de mapas,
cálculo geométrico de volúmenes, etc. en $[a,b]$ se calculan como
$${x_i} = {{a + b} \over 2} + {{b - a} \over 2}\cos \left( {{{\left( {2i + 1} \right)\pi } \over {2n + 1}}} \right)\,\,\,\,\,\,\,0 \le i \le n$$
Pafnuti Lvóvich Tchebyschev (1821 - 1894). El más prominente miembro de la escuela de matemáticas de St. Petersburg. Hizo
investigaciones en Mecanismos, Teoría de la Aproximación de Funciones, Teoría de los Números, Teoría de Probabilidades y
Teoría de Integración. Sin embargo, escribió acerca de muchos otros temas: formas cuadráticas, construcción de mapas,
cálculo geométrico de volúmenes, etc. en $[a,b]$ se calculan como
$${x_i} = {{a + b} \over 2} + {{b - a} \over 2}\cos \left( {{{\left( {2i + 1} \right)\pi } \over {2n + 1}}} \right)\,\,\,\,\,\,\,0 \le i \le n$$
%Para obtener los nodos en un vector
x=(a+b)/2+(b-a)/2*cos((2*(0:n)+1)*pi/(2*n+2));

Ejercicio 4 propuesto del tema 3. 
Ejercicio 6 propuesto del tema 3. 
Interpolación de Hermite
Mínimos cuadrados
En el caso de los métodos de interpolación, no siempre se consigue una mejor aproximación aumentado el número de puntos de interpoación (ver por ejemplo la función de Runge).
Además, cuando se considera un número grande de nodos la manipulación y evaluación el cálculo resulta muy costoso computacionalmente y puede llevar también problemas de redondeo importantes.
Con el siguiente método veremos que en el caso de que se tenga mucha información sobre la función en ciertos puntos, en lugar de aumentar de forma considerablemente el grado del polinomio en los métodos de interpolación, es más ventajoso utilizar la siguiente técnica.

Formulación algebraica del problema
El problema que tratamos de resolver es encontrar el polinomio $p$ de grado menor o igual a $k$ que minimiza la siguiente expresión $$\sum\limits_{j = 0}^n {{\omega _j}} {\left( {p\left( {{x_j}} \right) - f\left( {{x_j}} \right)} \right)^2}$$
Para ver cómo se puede formular algebraicamente este problema, consideremos un polinomio $p$ de grado $k$ $$p\left( x \right) = {a_o} + {a_1}x + {a_2}{x^2} + .. + {a_k}{x^k}$$ y las siguientes matrices $$a = \begin{pmatrix} {{a_k}} \\ {{a_{k-1}}} \\ {{a_{k-2}}} \\ \vdots \\ {{a_0}} \\ \end{pmatrix}$$ $$A = \begin{pmatrix} {\sqrt {{\omega _0}} \,x_0^k} & {\sqrt {{\omega _0}} \,x_0^{k - 1}} & {...} & {\sqrt {{\omega _0}} \,{x_0}}& {\sqrt {{\omega _0}} }\\ {\sqrt {{\omega _1}} \,x_1^k} & {\sqrt {{\omega _1}} \,x_1^{k - 1}} & {...} & {\sqrt {{\omega _1}} \,{x_1}}& {\sqrt {{\omega _1}} } \\ \vdots & \vdots & {...} & \vdots & \vdots \\ {\sqrt {{\omega _n}} \,x_n^k} & {\sqrt {{\omega _n}} \,x_n^{k - 1}} & {...} & {\sqrt {{\omega _n}} \,{x_n}}& {\sqrt {{\omega _n}} } \\ \end{pmatrix} $$ $$b = \begin{pmatrix} {\sqrt {{\omega _o}} \,f\left( {{x_o}} \right)} \\ {\sqrt {{\omega _1}} \,f\left( {{x_1}} \right)} \\ \vdots \cr {\sqrt {{\omega _n}} \,f\left( {{x_n}} \right)} \\ \end{pmatrix}$$
Teniendo en cuenta la norma euclidea $${\left\| {Aa - b} \right\|^2} = \sum\limits_{j = 0}^n {{\omega _j}} {\left( {p\left( {{x_j}} \right) - f\left( {{x_j}} \right)} \right)^2}$$
y los coeficientes del polinomio $p$ que se busca sería la solución del problema: $$\mathop { (Q) \,\,\,\,{\rm{minimizar}}}\limits_{x \in {{\mathbb R}^{k + 1}}} {\left\| {Ax - b} \right\|^2}$$
Resolución del probema Q mediante la factorización QR
El método que se propone es el siguiente
- Realizamos la factorización QR de A donde Q es ortogonal, es decir, ${Q^T}Q = Q{Q^T} = I$ y tiene dimensiones $(n+1)\text{x}(n+1)$ y R es una matriz triangular superior $(n+1)\text{x}\text{x}(k+1)$
- Consideramos en Q y R las siguientes submatrices:
- Q=[Y Z] con Y matriz $(n+1)\text{x}(k+1)$ y Z matriz $(n+1)\text{x}(n-k)$
- $R = \begin{pmatrix} {\widehat R} \\ 0 \\ \end{pmatrix}$ siendo ${\widehat R}$ es una matriz triangular superior$(k+1)\text{x}(k+1)$ y O es una matriz formada por ceros de orden $(n-k)\text{x} (k+1)$
- Los coeficientes del polinomio solución $$a = {\left( {{a_0},{a_1},...,{a_k}} \right)^T}$$ se obtienen resolviendo el sistema de ecuaciones lineales $$\widehat Ra = {Y^T}b$$ y el residual es $${\mathop{\rm Re}\nolimits} s = \left\| {{Z^T}b} \right\|$$
Por lo tanto, $${\left\| {Ax - b} \right\|^2} = {\left\| {QRx - b} \right\|^2} = {\left\| {Q\left( {Rx - {Q^T}b} \right)} \right\|^2} = $$ $${\left\| {Rx - {Q^T}b} \right\|^2} = {\left\| {\,\left( {_O^{\widehat R}} \right)x - \left( {_{{Z^T}}^{{Y^T}}} \right)b\,} \right\|^2} = {\left\| {\,\left( {_{ - {Z^T}b}^{\widehat Rx - {Y^T}b}} \right)\,} \right\|^2} = $$ $${\left\| {\,\widehat Rx - {Y^T}b\,} \right\|^2} + {\left\| {\,{Z^T}b\,} \right\|^2}$$
El mínimo valor del problema (Q) se obtiene para el valor de $x$ que hace cero el término $${\left\| {\,\widehat Rx - {Y^T}b\,} \right\|^2}$$.De la expresión anterior se deduce que equivalentemente se obtiene el valor mínimo para el valor $x$ solución del sistema $${\widehat Rx = {Y^T}b}$$
Ejercicio 11 propuesto del tema 3. 
Octave online
Octave es una alternativa a Matlab con un aspecto y unos comandos y sintasis similares. Se trata de un lenguaje interpretado de alto nivel. Lo puedes descargar desde su página oficial completamente gratis. Aquí tienes el enlace de descarga.
Pero además, puedes utilizar una versión en línea desde tu móvil en el caso de que no tengas a mano tu ordenador. Esta versión la tienes aquí: Octave online.
Integración numérica
Introducción
En este capítulo nos dedicaremos a encontrar una aproximación de la integral $\int\limits_a^b {f\left( x \right)dx} $ cuando $f$ es una función integrable en $[a,b]$. Analizaremos también el error que se comete en la aproximación y cómo obtener su valor con una precisión dada.
Este problema se plantea por varias razones:
- La posibilidad de aplicar la Regla de Barrow se restringe a una pequeña parte de funciones elementales que tienen primitivas también elementales. Muchas funciones, como por ejemplo $e^{x^2}$ que es continua, no tienen primitiva elemental.
- Aunque existiera un procedimiento para encontrar la primitiva, llegar a ella puede resultar en muchos casos tedioso. Pensemos por ejemplo en las funciones racionales o en aquellas que requieren de cambios de variable más o menos ingeniosos.
- Por otro lado, en muchas aplicaciones sólo se tiene una tabla de valores de la función $f$ o la posibilidad de obtener su valor en un número finito de puntos.
Estas razones obligan a encontrar métodos alternativos para calcular el valor de una integral definida en un intervalo de forma aproximada. Por razones históricas, el cálculo aproximado de integrales se denomina cuadratura dejando la denominación de integración para la resolución de ecuaciones diferenciales.
Veremos en este tema otras fórmulas utilizando polinomios interpoladores.
Métodos habituales para obtener fórmulas de cuadratura
Consideremos en primer lugar un polinomio $p$ interpolador de $f$ en $n+1$ nodos, se tendría $$\left\{ {{x_i}} \right\}_{i = 0}^n \subset \left[ {a,b} \right]\,\,\,\,\,\,\,\,\,\,\,\,p\left( {{x_i}} \right) = f\left( {{x_i}} \right)\,\,i = 0,1,...,n$$
En consecuencia, una primera aproximación del valor de la integral de $f$ en $[a,b]$ podría ser $$\int\limits_a^b {f\left( x \right)dx} \approx \int\limits_a^b {p\left( x \right)dx} $$
Considerando el polinomio de interpolación de Lagrange, se tendrá que: $$p\left( x \right) = \sum\limits_{i = 0}^n {f\left( {{x_i}} \right){l_i}\left( x \right)} \,\,\,\, , \,\,\,\,\,\,\, {l_i}\left( x \right) = \prod\limits_{j = 0\,\,\,j \ne i}^n {{{x - {x_j}} \over {{x_i} - {x_j}}}} \,\,\,\,\,\, 0 \le i \le n$$
y, por lo tanto, $$\int\limits_a^b {p\left( x \right)dx} = \sum\limits_{i = 0}^n {f\left( {{x_i}} \right)\int\limits_a^b {{l_i}\left( x \right)dx} } = $$ $$ = \left( {b - a} \right)\sum\limits_{i = 0}^n {f\left( {{x_i}} \right)\underbrace {\left( {{1 \over {b - a}}\int\limits_a^b {{l_i}\left( x \right)dx} } \right)}_{{w_i}}} $$
Este tipo de cuadratura se dice que es una fórmula interpolatoria. Los puntos ${w_i}$ se denominan pesos y los puntos ${x_i}$ son los nodos de la fórmula de cuadratura.
Para ello se divide el intervalo $[a,b]$ en $k$ subintervalos $$a = {\alpha _o} < {\alpha _1} < ... < {\alpha _n} = b$$ obteniendo la siguiente aproximación $$\int\limits_a^b {f\left( x \right)dx} = \sum\limits_{i = 1}^k {\int\limits_{{\alpha _{i - 1}}}^{{\alpha _i}} {f\left( x \right)dx} } $$
Posteriormente se aplica la fórmula de cuadratura a cada subintervalo donde se tiene en cuenta la siguiente transformación del intervalo $[a,b]$ en el intervalo $\left[ {{\alpha _{i - 1}},{\alpha _i}} \right]$ $$\begin{aligned} & \left[ {a,b} \right] &\to &\left[ {{\alpha _{i - 1}},{\alpha _i}} \right] \\ & x &\to & t = {\alpha _{i - 1}} + {{{\alpha _i} - {\alpha _{i - 1}}} \over {b - a}}\left( {x - a} \right) \end{aligned}$$ Este tipo de fórmulas se denominan de cuadratura compuestas y se analizan en el apartado 1.4.
Para calcular la calidad de una fórmula de cuadratura se define su grado de precisión o exactitud.
Veremos en primer lugar cómo obtener fórmulas de cuadratura elementales y el error asociado limitándonos a las fórmulas de Newton-Cotes. Posteriormente veremos cómo construir fórmulas de cuadratura compuesta para aproximar la integral con un error inferior a la precisión dada.
Fórmulas de cuadratura de Newton-Cotes
Estas fórmulas de cuadratura son de tipo interpolatorio $$\int\limits_a^b {f\left( x \right)dx} \approx \left( {b - a} \right)\sum\limits_{i = 0}^n {{w_i}f\left( {{x_i}} \right)} \,\,\,\,\,\,\,\,\,\,\,\,\,{w_i} = {1 \over {b - a}}\int\limits_a^b {{l_i}\left( x \right)dx} $$ donde los nodos se toman equidistantes.
En la práctica resulta de utilidad el siguiente resultado.
Con los resultados expuestos anteriormente vamos a ver que la construcción de las fórmulas de Newton-Cotes no precisa calcular los polinomios base de Lagrange y luego realizar las integrales para obtener los correspondientes pesos.
Veamos cómo aplicar estos resultados para calcular las primeras fórmulas de Newton-Cotes.
Primera fórmula de Newton-Cotes (n=1)
Consideramos dos nodos en el intervalo $[a,b]$, esto es, $x_0=a$ y $x_1=b$. La fórmula de cuadratura es $$\int\limits_a^b {f\left( x \right)dx} \approx \left( {b - a} \right)\left[ {{\omega _o}f\left( a \right) + {\omega _1}f\left( b \right)} \right]$$
Para calcular los pesos se considera el intervalo $[0,1]$ y se resuelve el sistema $$\begin{aligned} & k = 0\,\,\,\,\,\,\,\,\,&1 = \int\limits_0^1 {dx} = {\omega _o} + {\omega _1} \\ & k = 1\,\,\,\,\,\,\,\,\,&{1 \over 2} = \int\limits_0^1 {xdx} = {\omega _1} \end{aligned}$$
La solución del sistema es ${\omega _o} = {\omega _1} = {1 \over 2}$. Por lo tanto, $$\int\limits_a^b {f\left( x \right)dx} \approx {{b - a} \over 2}\left[ {f\left( a \right) + f\left( b \right)} \right]$$ Esta fórmula de Newton-Cotes de dos puntos se llama fórmula del trapecio.

Segunda fórmula de Newton-Cotes (n=2)
En este caso el número de nodos es 3: $x_o=a$, $x_1=\frac{a+b}{2}$ y $x_2b$. La fórmula de cuadratura en este caso es $$\int\limits_a^b {f\left( x \right)dx} \approx \left( {b - a} \right)\left[ {{\omega _o}f\left( a \right) + {\omega _1}f\left( {{{a + b} \over 2}} \right) + {\omega _2}f\left( b \right)} \right]$$ Para determinar los nodos consideramos el intervalo $[-1,1]$. Resolviendo el sistema de 3 ecuaciones con 3 incógnicas, obtenemos ${\omega _o} = {\omega _2} = {1 \over 6}$, ${\omega _1} = {2 \over 3}$. Por lo tanto: $$\int\limits_a^b {f\left( x \right)dx} \approx {{\left( {b - a} \right)} \over 6}\left[ {f\left( a \right) + 4f\left( {{{a + b} \over 2}} \right) + f\left( b \right)} \right]$$
Esta regla se llama regla de Simpson.
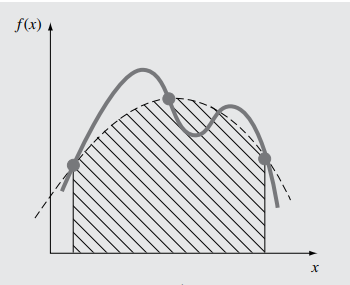
Fórmula de Newton-Cotes con n=3
En este caso el número de nodos es 4: $x_0=a$, $x_1=a+\frac{b-a}{3}$, $x_2=a+2 \frac{b-a}{3}$ y $x_3=b$. La fórmula de cuadratura es $$\int\limits_a^b {f\left( x \right)dx} \approx \left( {b - a} \right)\left[ {{\omega _o}f\left( a \right) + {\omega _1}f\left( { {{2a+b} \over 3}} \right) + } \right.{\rm{ }}$$ $$\left. +{{\omega _2}f\left( {{{a+2b} \over 3}} \right) + {\omega _3}f\left( b \right)} \right]$$ Para determinar los nodos consideramos el intervalo $[0,3]$ y se resuelve el sistema de 4 ecuaciones con 4 incógnitas asociado, obteniendo ${\omega _o} = {\omega _3} = {1 \over 8}$, ${\omega _1} = {\omega _2} = {3 \over 8}$ Por lo tanto: $$\int\limits_a^b {f\left( x \right)dx} \approx $$ $$ \approx {{\left( {b - a} \right)} \over 8}\left[ {f\left( a \right) + 3f\left( {{{2a + b} \over 3}} \right) + 3f\left( {{{a + 2b} \over 3}} \right) + f\left( b \right)} \right] $$ Esta fórmula se llama regla de los tres octavos.
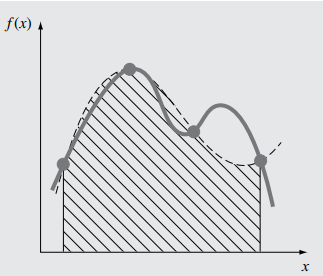
De forma análoga pueden obtenerse las siguientes fórmulas de Newton-Cotes.
Error en la fórmula de cuadratura de Newton-Cotes.
Vamos a analizar en este apartado el error de las fórmulas de cuadratura de Newton-Cotes. El error de la aproximación es la diferencia entre el valor exacto y el aproximado, es decir: $$E = \int\limits_a^b {f\left( x \right)dx} - \left( {b - a} \right)\sum\limits_{j = 0}^n {{\omega _j}f\left( {{x_j}} \right)} $$ El siguiente resultado nos da una expresión para este error.
Error en la fórmula del trapecio ($n=1$)
Consideremos la fórmula de Newton-Cotes para $n=1$, que es impar. Tomamos $m=n+1=2$. Se tiene que $$\begin{aligned} E=&\color{red}{\int\limits_a^b {f\left( x \right)dx}} \color{black}{-} \color{green}{{{b - a} \over 2}\left( {f\left( a \right) + f\left( b \right)} \right)} \\ E=&{C_1} h^3 f''\left( \xi \right) \end{aligned}$$ Para determinar $C_1$, consideramos la función $f(x)=(x-a)^m=(x-a)^2$. Para esta función se tiene que por un lado se cumple $$\color{red}{\int\limits_a^b {f(x)dx}} \color{black}{=\int\limits_a^b {{(x-a)^2}dx} = {1 \over 3}{\left( {b - a} \right)^3} =} \color{red}{{ {h^3} \over 3}}$$ y por otro $$\color{green}{{{b - a} \over 2}\left( {f\left( a \right) + f\left( b \right)} \right)} \color{black}{= {{b - a} \over 2}\left( {0 + {{\left( {b - a} \right)}^2}} \right) =} {{{{\left( {b - a} \right)}^3}} \over 2} = \color{green}{ \frac {h^3} {2}}$$ Por lo tanto, $${C_1}{h^3}{f^{''}}\left( \xi \right) = {{{h^3}} \over 3} - {{h^3} \over 2}$$es decir, $$2 {C_1} = {1 \over 3} - {1 \over 2} = - {1 \over 6}$$ $${C_1} = - {1 \over 12}$$
Error en la fórmula de Simpson
Consideremos la fórmula de Newton-Cotes para $n=2$ que es par, consideramos $m=n+2=4$. . Se tiene que $$\begin{aligned} E=&\int\limits_a^b {f\left( x \right)dx} - {{{b - a} \over 6}\left[ {f\left( a \right) + 4f\left( {{{a + b} \over 2}} \right) + f\left( b \right)} \right]} \\ E=&{C_2} h^5 f''\left( \xi \right) \end{aligned}$$ Para determinar $C_2$ consideramos la función $f(x)=(x-a)^m=(x-a)^4 $. Se tiene que por un lado se cumple $$\int\limits_a^b {{(x-a)^4}dx} = {1 \over 5}{\left( {b - a} \right)^5} = { {(2h)^5} \over 5}$$ y por otro $${{b - a} \over 6}\left[ {0 + 4\, \cdot {h^4} + {(2h)^4}} \right] = {{2h^5} \over 6} \cdot 20$$
Error en la fórmula de cuadratura 3/8
Consideremos la fórmula de Newton-Cotes para $n=3$, que es impar. Tomamos $m=n+1=4$. Se tiene que $$E=\int\limits_a^b {f\left( x \right)dx} - $$ $${{\left( {b - a} \right)} \over 8}\left[ {f\left( a \right) + 3f\left( {{{2a + b} \over 3}} \right) + 3f\left( {{{a + 2b} \over 3}} \right) + f\left( b \right)} \right] $$
Para determinar $C_3$ se considera la función $f(x)=(x-a)^m=(x-a)^4$. Se cumplirá $$\int\limits_a^b {{(x-a)^4}dx} = {1 \over 5}{\left( {b - a} \right)^5} = { {(3h)^5} \over 5}$$ $${{3h} \over 8}\left[ 0 + 3\, \cdot {h^4} + 3\, \cdot (2h)^4 + (3h)^4 \right] = {{99h^5} \over 2} $$ Por lo tanto, $$E={C_3} h^5 f^{(4}\left( \xi \right)=\frac{-9}{10}h^5$$ $$4!{C_3} = {{ - 9} \over {10}}\,\,\,\,\,\, \Rightarrow \,\,\,{C_3} = - {3 \over {80}}$$
En la siguiente imagen se muestra la expresión del resto para cada una de las fórmulas de Newton-Cotes vistas anteriormente.
Fórmulas compuestas. Métodos adaptativos
Cuando la distancia entre los nodos $h$ es de longitud grande, mayor que 1, el error que se comete puede ser grande. Por ello, cuando el intervalo $[a,b]$ es grande se divide el intervalo $[a,b]$ en $k$ subintervalos $$a = {\alpha _o} < {\alpha _1} < ... < {\alpha _n} = b$$ y se calcula: $$\int\limits_a^b {f\left( x \right)dx} = \sum\limits_{i = 1}^k {\int\limits_{{\alpha _{i - 1}}}^{{\alpha _i}} {f\left( x \right)dx} } $$ aplicando la fórmula de cuadratura a cada uno de los subintervalos $[{\alpha _{i-1}},{\alpha _i}]$.
Si llamamos $I$ a la aproximación de la integral $$\int\limits_a^b {f\left( x \right)dx} = I + E \,\,\, \text{con} \,\,E = {C_n}{h^{m + 1}}{f^{(m}}\left( \xi \right)$$ siendo $$m = \left\{ \begin{aligned} &n + 1\,\,si\,\,n\,\,impar \\ &n + 2\,\,si\,\,n\,\,par \\ \end{aligned} \right.$$
Aplicando la misma fórmula a los intervalos $[a,\frac{a+b}{2}]$ y $[\frac{a+b}{2},b]$ se tendrá, $$\begin{aligned} \int\limits_a^{\frac {a+b}{2}} {f\left( x \right)dx} &= {I_1} + {E_1} = {I_1} + {C_n}{\left( {{h \over 2}} \right)^{m + 1}}{f^{(m}}\left( {{\xi _1}} \right)\\ & {\xi _1} \in \left[ {a,{{a + b} \over 2}} \right] \end{aligned}$$ $$\begin{aligned} \int\limits_{{{a + b} \over 2}}^b {f\left( x \right)dx} &= {I_2} + {E_2} = {I_2} + {C_n}{\left( {{h \over 2}} \right)^{m + 1}}{f^{(m}}\left( {{\xi _2}} \right)\\ &{\xi _2} \in \left[ {{{a + b} \over 2},b} \right] \end{aligned}$$
Si $[a,b]$ es pequeño, $$I + E{\mkern 1mu} {\mkern 1mu} = {I_1} + {I_2} + {C_n}{{{h^{m + 1}}} \over {{2^m}}}\left[ {{{{f^{(m}}\left( {{\xi _1}} \right) + {f^{(m}}\left( {{\xi _2}} \right)} \over 2}} \right]$$ dado que el intervalo es pequeño, $$I + E{\mkern 1mu} {\mkern 1mu} \approx {I_1} + {I_2} + \underbrace {{C_n}{{{h^{m + 1}}} \over {{2^m}}}{f^{(m}}\left( \xi \right)}_{E/{2^m}}$$ $$I + E \approx {I_1} + {I_2} + {E \over {{2^m}}}$$ $${{{2^m} - 1} \over {{2^m}}}E \approx {I_1} + {I_2} - I$$ $$E \approx {{{2^m}} \over {{2^{m - 1}}}}\left( {{I_1} + {I_2} - I} \right)$$
Fijada una precisión $\epsilon$ deseada de la integral, se describe la estrategia para obtener la aproximación con la precisión deseada.
- Elegimos una fórmula de Newton-Cotes para aproximar la integral en $[a,b]$.
- Subdividimos el intervalo $[a,b]$ en dos subintervalos de la misma longitud y calculamos las aproximaciones de las integrales $I_1$ e $I_2$ en ambos intervalos, con las correspondientes estimaciones de los errores $E_1$ y $E_2$. Definimos los vectores $I=[I_1, \,\,I_2]$ y $E=[E_1, \,\,E_2]$
- Elegimos una fórmula de Newton-Cotes para aproximar la integral en $[a,b]$.
- Subdividimos el intervalo $[a,b]$ en dos subintervalos de la misma longitud y calculamos las aproximaciones de las integrales $I_1$ e $I_2$ en ambos intervalos, con las correspondientes estimaciones de los errores $E_1$ y $E_2$. Definimos los vectores $I=[I_1, \,\,I_2]$ y $E=[E_1, \,\,E_2]$
- Si la suma de los errores, sum(E), es inferior a $\epsilon$, tomamos la suma de las aproximaciones $I$ como valor aproximado de la integral y se habrá terminado. Si no es así, $sum(E) \ge \epsilon$, entonces vamos al paso siguiente.
- Buscamos el error $E_k$ más grande de los contenidos en el vector $E$. Subdividimos el intervalo asociado a $E_k$ en dos mitades y calculamos las aproximaciones de la integral en cada una de las mitades y los correspondietes errores. Eliminamos $I_k$ y $E_k$ y ponemos en su lugar los dos valores de la integral calculados y los correspondientes errores. Volvemos al paso 3.
x=[a (a+b)/2 b]
[i1 e1]=iehardy(x(1),x(2),f)
[i2 e2]=iehardy(x(2),x(3),f)
I=[i1 i2];E=[e1 e2];
error=sum(E);
if error<ea
itg=sum(I);
[itg error]
else
[s,k]=max(E)
end
parar=0
while parar==0
xn=(x(k)+x(k+1))/2
x=[x(1:k) xn x(k+1:end)]
[i1 e1]=iehardy(x(k),xn,f);
[i2 e2]=iehardy(xn,x(k+2),f);
E=[E(1:k-1) e1 e2 E(k+1:end)];
I=[I(1:k-1) i1 i2 I(k+1:end)];
error=sum(E);
if error < ea
itg=sum(I);
[itg error]
parar=1;
else
[s,k]=max(E);
end
end
Si se considera el error absoluto en la precisión de la solución el algoritmo se detiene si $E < \epsilon_a$. Si se usa el error relativo, el algoritmo se detenderá si $E < \epsilon_r|I|$. A menudo se utiliza un test de parada que combina ambos errores: $$E < \epsilon_a+\epsilon_r |I|$$ En este caso, usualmente, si la integral es un número grande, el algoritmo se detiene cuando el error relativo es inferior a $\epsilon_r$, mientras que si $|I|$ es pequeño, el algoritmo finaliza cuando el error absoluto es inferior a $\epsilon_a$.
Cálculo de Integrales impropias
En este apartado, veremos cómo proceder cuando el intervalo $[a,b]$ no es acotado. En el primer apoartado analizaremos el caso en el que $a$ o $b$ o ambos no son finitos (integrales impropias de primera especie) y en el segundo apartado cuando $f$ tenga una singularidad en un punto $x_o$ en $[a,b]$ de forma que se cumple $\mathop {\lim }\limits_{x \to {x_o}} \left| {f\left( x \right)} \right| = + \infty $ (integrales impropias de segunda especie).
Integrales impropias de primera especie
Consideraremos en este caso integrales del tipo $$\int\limits_a^\infty {f\left( x \right)dx} = \mathop {\lim }\limits_{b \to \infty } \int\limits_a^b {f\left( x \right)dx} $$ donde $f$ es continua. Cuando el límite anterior existe, la integral impropia es convergente. En este caso se tendrá que $$\mathop {\lim }\limits_{b \to \infty } \int\limits_b^\infty {f\left( x \right)dx} = 0$$ En primer lugar se hallará un valor de $b$ de forma que $$\left| {\int\limits_b^\infty {f\left( x \right)dx} } \right| < {\varepsilon \over 2}$$y luego se buscará una aproximación de la intengral $Itg$ de forma que $$\left| {\int\limits_a^b {f\left( x \right)dx} - Itg} \right| < {\varepsilon \over 2}$$ De forma análoga se podrá calcular las integrales $${\int\limits_{ - \infty }^a {f\left( x \right)dx} }$$
En el caso de una integral de la forma $${\int\limits_{ - \infty }^\infty {f\left( x \right)dx} }$$ se tendrá en cuenta que $$\int\limits_{ - \infty }^\infty {f\left( x \right)dx} = \int\limits_{ - \infty }^0 {f\left( x \right)dx} + \int\limits_0^\infty {f\left( x \right)dx} $$ buscando una aproximación de cada una de ellas con un error menor que $\epsilon/2$. Alternativamente se puede buscar números $a<0$ y $b>0$ de forma que $$\left| {\int\limits_{ - \infty }^a {f\left( x \right)dx} } \right| < {\varepsilon \over 4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| {\int\limits_b^\infty {f\left( x \right)dx} } \right| < {\varepsilon \over 4}\,\,\,\,\,\,\,\,\,\left| {\int\limits_a^b {f\left( x \right)dx} } \right| < {\varepsilon \over 2}$$
Integrales impropias de segunda especie
En este tipo de integrales la función $f$ es continua en $[a,b]$ salvo en un punto $x_0$ donde $$\mathop {\lim }\limits_{x \to {x_0}} \left| {f\left( x \right)} \right| = + \infty $$
Caso 1 Si el punto $x_0=a$ será $$\int\limits_a^b {f\left( x \right)dx} = \mathop {\lim }\limits_{\delta \searrow 0} \int\limits_{a + \delta }^a {f\left( x \right)dx} $$ Caso 2 Si el punto $x_0=b$ será $$\int\limits_a^b {f\left( x \right)dx} = \mathop {\lim }\limits_{\delta \searrow 0} \int\limits_a^{b - \delta } {f\left( x \right)dx} $$ Caso 3 Si $X_0$ es un punto interior se define esta integral impropia de la forma siguiente: $$\int\limits_a^b {f\left( x \right)dx} = \mathop {\lim }\limits_{\delta \searrow 0} \int\limits_a^{{x_o} - \delta } {f\left( x \right)dx} + \mathop {\lim }\limits_{\delta \searrow 0} \int\limits_a^{{x_o} + \delta } {f\left( x \right)dx} $$
Dependiendo del caso se actúa de la siguiente manera:
Caso 1 Se busca $\delta$ cumpliendo $$\left| {\int\limits_a^{a + \delta } {f\left( x \right)dx} } \right| < {\varepsilon \over 2}$$ y luego una aproximación verificando $$\left| {\int\limits_{a + \delta }^b {f\left( x \right)dx} } \right| < {\varepsilon \over 2}$$ Se procede de forma análoga en el caso 2.
Caso 3 Se busca un valor de $\delta > 0$ verificando $$\left| {\int\limits_{{x_o} - \delta }^{{x_o}} {f\left( x \right)dx} } \right| + \left| {\int\limits_{{x_o}}^{{x_o} + \delta } {f\left( x \right)dx} } \right| < {\varepsilon \over 2}$$ Después se buscan aproximaciones de las integrales cumpliendo $$\left| {\int\limits_a^{{x_o} - \delta } {f\left( x \right)dx} } \right| < {\varepsilon \over 4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| {\int\limits_{{x_o} + \delta }^b {f\left( x \right)dx} } \right| < {\varepsilon \over 4}$$
Octave online
Octave es una alternativa a Matlab con un aspecto y unos comandos y sintasis similares. Se trata de un lenguaje interpretado de alto nivel. Lo puedes descargar desde su página oficial completamente gratis. Aquí tienes el enlace de descarga.
Pero además, puedes utilizar una versión en línea desde tu móvil en el caso de que no tengas a mano tu ordenador. Esta versión la tienes aquí: Octave online.