Métodos Numéricos
Elena E. Álvarez Saiz
Red Educativa Digital Descartes.
Universidad de Cantabria
Título de la obra:
MÉTODOS NUMÉRICOS
Autores:
Elena E. Alvarez Saiz
Diseño del libro: Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Primera Edición
LICENCIA
Tabla de contenido
Integración Numérica de
Ecuaciones Diferenciales
Introducción
En Ingeniería, las ecuaciones diferenciales tienen gran importancia para modelar y explicar el comportamiento de muchos fenómenos. Igualmente, las leyes físicas se expresan con frecuencia como una razón de cambio, por ejemplo, la caída de un cuerpo, el cambio de temperatura, las variaciones del caudal de una corriente de agua, la deformación de un elemento de hormigón, etc. En la siguiente escena se muestra un ejemplo de aplicación de las ecuaciones diferenciales a un sistema muelle-resorte.
En el siguiente ejemplo, las ecuaciones diferenciales modelizan al vaciado de un tanque.
En este capítulo vamos a estudiar la resolución numérica de dos problemas asociados a las ecuaciones diferenciales ordinarias:
- el problema de Cauchy o problema de valor inicial
- el problema de contorno.
Formulación del problema de valor inicial
Esta forma genérica permite la formulación de muchos problemas. Veamos algún ejemplo.
Existencia y unicidad
Dado el problema $$\left\{ \begin{aligned} & y'\left( t \right) = f\left( {t,y\left( t \right)} \right)\,\,\,\,\,\,\,\,\,t \in \left[ {{t_o},{t_f}} \right] \\ & y\left( {{t_o}} \right) = {y_0} \end{aligned} \right.$$ con $$f:\left[ {{t_o},{t_f}} \right]\text{x}{\mathbb R^n} \to \mathbb R^n$$ si $f$ es continua y acotada en un dominio que contenga a $(t_0,y_o)$ entonces el problema tiene al menos una solución. Para que la solución sea única se puede exigir que la función cumpla la condición de Lipschitz para la variable $y$, es decir, exista $L> 0$ de forma que para todo $t$ en $[t_0,t_f]$ $$\left\| {f\left( {t,{y_1}} \right) - f\left( {t,{y_2}} \right)} \right\| \le L\left\| {{y_1} - {y_2}} \right\|$$
Métodos de Runge-Kutta
En este apartado estudiaremos los métodos de un paso, que son aquellos para los que dado el problema $$y'\left( t \right) = f\left( {t,y\left( t \right)} \right)\,\,\,\,\,\,\,\,\,t \in \left[ {{t_o},{t_f}} \right] $$
la integración numérica del problema consiste en determinar unos instantes $${t_o} < {t_1} < {t_2} < ... < {t_N} = {t_f} \,\,\,\,\,\,h_n=t_{n+1}-t_n$$
y valores $$\left\{ {{y_o},\,\,{y_1},\,\,{y_2}...,\,\,{y_N}} \right\}$$ de forma que a partir de $$y\left( {{t_n}} \right) \approx {y_n}$$ se pueda obtener la aproximación de $y_{n+1}$.
En la imagen siguiente se muestra, para una ecuación diferenciable de primer orden, la solución de un problema de valor inicial y la solución aproximada con 7 pasos. El método numérico deberá indicar cómo obtener cada punto de la solución numérica a partir del anterior.
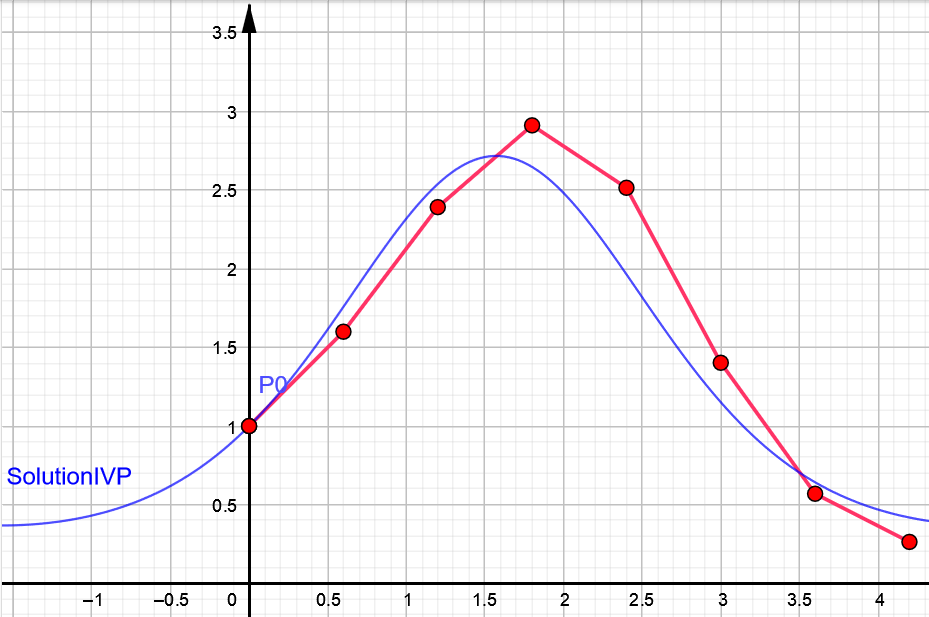
Para encontrar la solución, en $y(t_{n+1})$ a partir de $y(t_n)$, se considera $$y\left( {{t_{n + 1}}} \right) = y\left( {{t_n}} \right)\, + \int\limits_{{t_n}}^{{t_n+h_n}} {y'\left( t \right)dt} $$ es decir, $$y\left( {{t_{n + 1}}} \right) = y\left( {{t_n}} \right)\, +\color{blue}{ \int\limits_{{t_n}}^{{t_{n + 1}}} {f\left( {t,y\left( t \right)} \right)dt}} $$ Utilizando una fórmula de cuadratura para obtener la integral, se tendrá $$y\left( {{t_{n + 1}}} \right) \approx {y_n} + \color{blue}{{h_n}\sum\limits_{i = 1}^m {{b_i}f\left( {{t_n} + {c_i}{h_n},y\left( {{t_n} + {c_i}{h_n}} \right)} \right)}} $$ donde $m$ es el número de nodos en la fórmula de cuadratura, $b_i$ son los pesos y los $c_i$ son los números entre 0 y 1 que definen los nodos $$t_{n,i}=t_n+c_i h_n$$ en el intervalo $[t_n,t_{n+1}]$.
En la imagen se representa un ejemplo con $m=6$ donde se muestran los valores $c_i$ y $t_{h,i}$.

Para obtener la aproximación de $y(t_{n+1})$ hay que calcular una aproximación de los valores $y(t_n+c_ih_n)$ $${y_{n,i}} = y\left( {{t_n} + {c_i}{h_n}} \right) \approx y\left( {{t_n}} \right) + \int\limits_{{t_n}}^{{t_n} + {c_i}{h_n}} {f\left( {t,y\left( t \right)} \right)dt} $$ con alguna fórmula de cuadratura $$y\left( {{t_n} + {c_i}{h_n}} \right) \approx {y_n} + {h_n}\sum\limits_{j = 1}^m {{a_{ij}} {\underbrace {f({t_n} + {c_j}{h_n},{y_{n,j}})}_{{K_{n,j}}} } } $$
Los métodos de Runge-Kutta pueden describirse a trávés del llamado tablero de Butcher donde se pueden disponer los parámetros $A$, $b$ y $c$ de la forma siguiente:
| $c$ | $A$ |
| $b^T$ |
Cuando los métodos son explícitos la matriz es triangular inferior.
Vamos a ver algunos métodos de Runge -Kutta con su tablero de Butcher.
Método de Euler
Como hemos indicado anteriormente, $${y(t_{n + 1})} = {y(t_n)} +\color{blue}{ \int\limits_{{t_n}}^{{t_{n + 1}}} {f\left( {t,y\left( t \right)} \right)dt}}$$
Consideremos la fórmula de cuadratura más sencilla para calcular la integral $$\int\limits_{{t_n}}^{{t_n} + {h_n}} {g\left( t \right)dt} \approx {h_n}g\left( {{t_{_n}}} \right)$$
se tendrá que $${y(t_{n + 1})} = {y(t_n)} +\color{blue}{ \int\limits_{{t_n}}^{{t_{n + 1}}} {f\left( {t,y\left( t \right)} \right)dt}}$$
$${y(t_{n + 1})} \approx {y_{n+1}}={y_n} + \color{blue}{{h_n}f\left( {{t_n},{y_n}} \right)}$$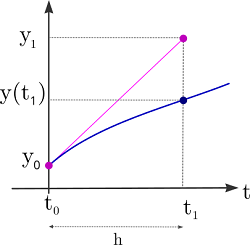
El tablero de Butcher es
| $0$ | $0$ |
| $1$ |
Escribimos el código Matlab para obtener también los cálculos.
f=@(t,y) 0.7*y-t^2+1;%Función
a=1;b=2;y0=1;%Intervalo
N=10;%Pasos (N+1 puntos)
h=(b-a)/N; %Longitud del paso
t(1)=a;
y(1)=y0;
for n=1:N
t(n+1)=t(n)+h;
%dy/dt=f(t,y)
y(n+1)=y(n)+h*f(t(n),y(n));
end
[t y]
hold on
%Solución exacta
syms s(u)
eqn=diff(s)==f(u,s)
cond=s(a)==y0
sol(u)=dsolve(eqn,cond)
t1=linspace(a,b,50);
plot(t1,sol(t1))
hold off
xlabel(['Metodo de Euler con N=',num2str(N),' pasos'])
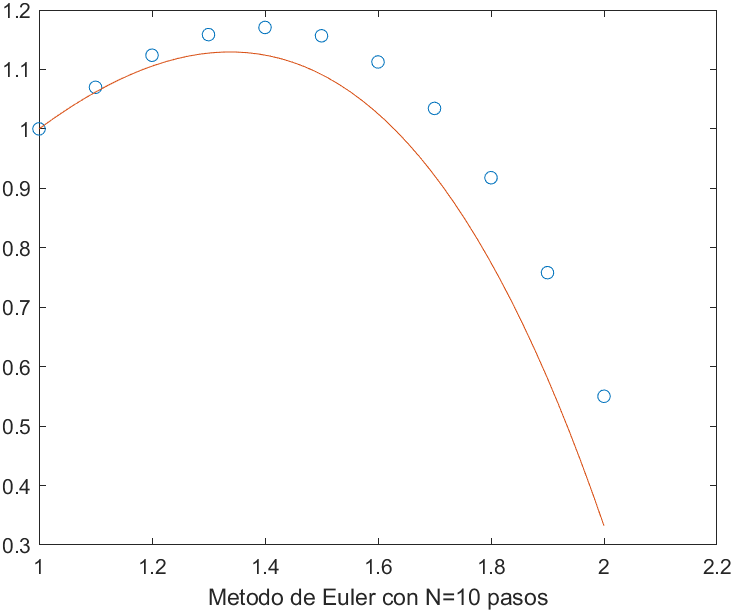 Nótese que en cada paso se necesita del valor $y(t_n)$, por tanto cuanto más cercano sea el valor $y_n$ del $y(t_n)$ real más preciso será el método. Para calcular $y_1$ se utiliza el valor $y_o$ pero cuando calculamos $y_2$ sustituimos el valor exacto $y(t_1)$ desconocido por su valor aproximado $y_1$, para calcular $y_3$, sustituimos el valor $y(t_2)$ por su valor aproximado $y_2$, y así sucesivamente.
Nótese que en cada paso se necesita del valor $y(t_n)$, por tanto cuanto más cercano sea el valor $y_n$ del $y(t_n)$ real más preciso será el método. Para calcular $y_1$ se utiliza el valor $y_o$ pero cuando calculamos $y_2$ sustituimos el valor exacto $y(t_1)$ desconocido por su valor aproximado $y_1$, para calcular $y_3$, sustituimos el valor $y(t_2)$ por su valor aproximado $y_2$, y así sucesivamente.
Método de Heun
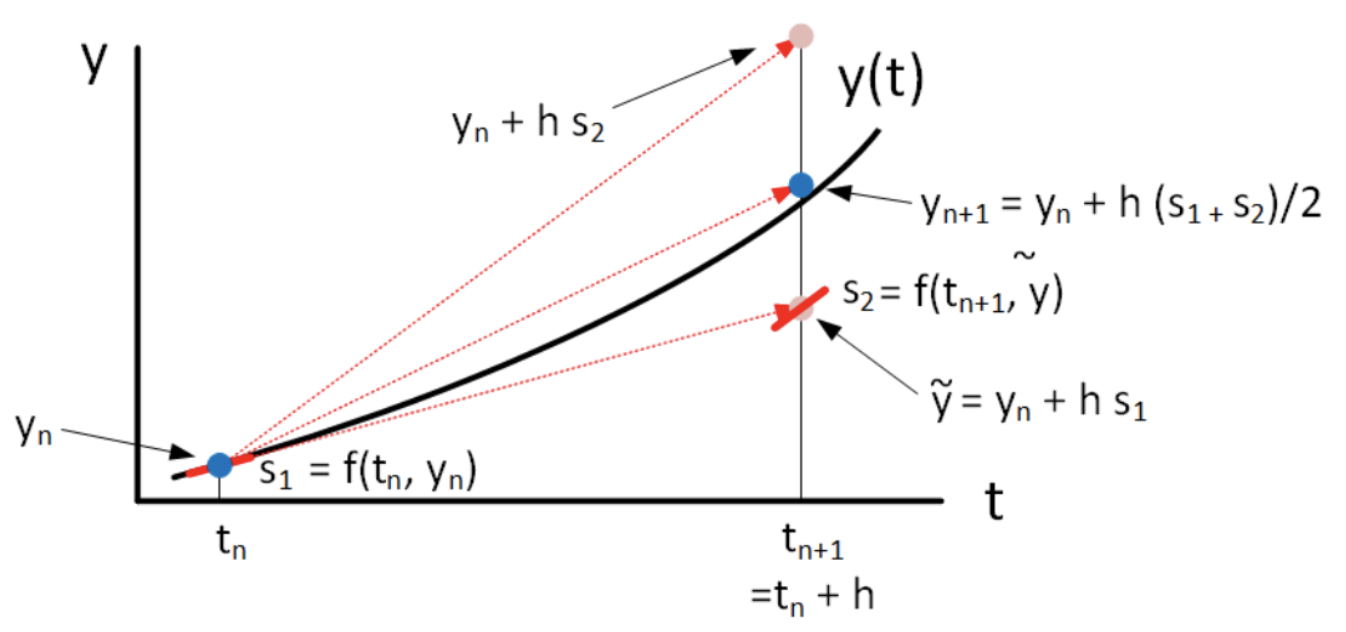
Consideremos la fórmula de cuadratura del trapecio $$\int\limits_{{t_n}}^{{t_n} + {h_n}} {g\left( t \right)dt} \approx {{{h_n}} \over 2}\left( {g\left( {{t_{_n}}} \right) + g\left( {{t_{n + 1}}} \right)} \right)$$
Utilizando la aproximación que ya tenemos ${y_n} \approx y\left( {{t_n}} \right)$ podremos obtener $y_{n+1}$ de la forma siguiente $${y_{n + 1}} = {y_n} + {{{h_n}} \over 2}\left[ {f\left( {{t_n},{y_n}} \right) + f\left( {{t_{n + 1}},\color{blue}{{y_{n + 1}}}} \right)} \right]$$ y considerando la fórmula de Euler para aproximar $\color{blue}{{y_{n + 1}}}$ $${y_{n + 1}} = {y_n} + {{{h_n}} \over 2}\left[ {f\left( {{t_n},{y_n}} \right) + f\left( {{t_n} + {h_n},\color{blue}{\underbrace {{y_n} + {h_n}f\left( {{t_n},{y_n}} \right)}_{Euler}}} \right)} \right]$$
Este método podría escribirse así: $$\begin{aligned} & {t_{n,1}} = {t_n}\,\,\,\,{t_{n,2}} = {t_n}+h_n \\ & \,\,\,\,\,\,\,\,\,\,{y_{n,1}} = {y_n} \\ & \,\,\,\,\,\,\,\,\,\,{y_{n,2}} = {y_n} + {h_n}f\left( {{t_{n,1}},{y_{n,1}}} \right) \\ & {y_{n+1}} = {y_n} + {{{h_n}} \over 2}\left[ {f\left( {{t_{n,1}},{y_{n,1}}} \right) + f\left( {{t_{n,2}},{y_{n,2}}} \right)} \right] \\ \end{aligned}$$ En este caso, $m=2$, $c_1=0$, $c_2=1$, $b_1=1/2$. $b_2=1/2$.
También podría escribirse de la forma siguiente: $$\begin{aligned} & \,\,\,\,\,\,\,\,\,\,{K_{n,1}} = f\left( t_n,y_n \right) \\ & \,\,\,\,\,\,\,\,\,\,{K_{n,2}} = f\left( {t_n}+h_n, y_n + h_n K_{n,1} \right) \\ & {y_{n+1}} = {y_n} + {{{h_n}} \over 2}\left[ {K_{n,1}} + {K_{n,2}} \right] \\ \end{aligned}$$
El tablero de Butcher es
$$\begin{array} {r|r r }
0 & 0 & 0 \\
1 & 1 &0 \\
\hline
& 1/2 & 1/2 \\
\end{array}$$
t0=0;tf=3;%Intervalo
N=30;%Pasos (N+1 puntos)
h=(tf-t0)/N; %Longitud del paso
tn=t0;t=[tn];yn=1;y=[yn];
for n=1:N %
K1=f(tn,yn);
K2=f(tn+h,yn+h*K1);
yn1=yn+(K1+K2)*h/2;
yn=yn1; tn=tn+h;
y=[y yn];t=[t tn];
end
plot(t,y,'*')
Llamando $y_1=y$, $y_2=y'$, se tiene
$$\begin{aligned} &{y'_1} = {y_2} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, {y'_2} = - 7seny - 0.1\cos t \\ &{y_1}\left( 0 \right) = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,{y_2}\left( 0 \right) = 1 \end{aligned} $$ En este caso, $$ \left( \begin{aligned} {{y'_1}\left( t \right)} \\ {{y'_2}\left( t \right)} \\ \end{aligned} \right)=\left( \begin{aligned} {{y_2}} \\ {-7sen({y_1})-0.1cos(t)} \\ \end{aligned} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \left( \begin{aligned} {{y_1}\left( 0 \right)} \\ {{y_2}\left( 0 \right)} \\ \end{aligned} \right)=\left( \begin{aligned} {{0}} \\ {1} \\ \end{aligned} \right)$$El código para resolver la ode con matlab considerando $N=30$ pasos será.
Método de Kutta de tres etapas
Consideremos ahora la fórmula de cuadratura de tres puntos $$\int\limits_{{t_n}}^{{t_n} + {h_n}} {g\left( t \right)dt} \approx {{{h_n}} \over 6}\left[ {g\left( {{t_n}} \right) + 4g\left( {{t_n} + \\ {1 \over 2}{h_n}} \right) + g\left( {{t_n} + {h_n}} \right)} \right]$$ En este caso, $m=3$, $c_1=0$, $c_2=1/2$, $c_3=1$, $b_1=1/6$, $b_2=3/2$, $b_3=1/6$. Entonces $${y_{n + 1}} = {y_n} + {{{h_n}} \over 6}\left[ {f\left( {{t_n},{y_n}} \right) + 4f\left( {{t_n} + {1 \over 2}{h_n},y\left( {{t_n} + {1 \over 2}{h_n}} \right)} \right)} \right.$$ $${ + f\left( {{t_{n + 1}},y\left( {{t_{n + 1}}} \right)} \right)}$$
Esto podría escribirse así: $$\begin{aligned} & {t_{n,1}} = {t_n}\,\,\,,\,\,\,{t_{n,2}} = {t_n}+h_n/2\,\,\,,\,\,\,{t_{n,3}} = {t_n}+h_n \\ & \,\,\,\,\,\,\,\,\,\,{y_{n,1}} = {y_n} \\ & \,\,\,\,\,\,\,\,\,\,{y_{n,2}} = {y_n} + \frac{{h_n}}{2} f\left( {{t_{n,1}},{y_{n,1}}} \right) \\ & \,\,\,\,\,\,\,\,\,\,{y_{n,3}} = {y_n} + {h_n}\left[ {-f\left( {{t_{n,1}},{y_{n,1}}} \right) + 2f\left( {{t_{n,2}},{y_{n,2}}} \right)} \right] \\ & {y_n} = {y_n} + {{{h_n}} \over 6}\left[ {f\left( {{t_{n,1}},{y_{n,1}}} \right) + 4f\left( {{t_{n,2}},{y_{n,2}}} \right) + f\left( {{t_{n,3}},{y_{n,3}}} \right)} \right] \end{aligned}$$ También podría escribirse de la forma siguiente:
El tablero de Butcher es $$\begin{array} {r|r r r } 0 & 0 & 0 & 0 \\ 1/2 & 1/2 & 0 & 0 \\ 1 & -1 & 2 & 0 \\ \hline & 1/6 & 4/6 & 1/6 \\ \end{array}$$
Se incluyen a modo de resumen los correspondientes tableros de Butcher de algunos métodos de Runge-Kutta.
Método de Euler $$\begin{array} {r|r } 0 & 0 \\ \hline & 1 \\ \end{array}$$ Método de Heun $$\begin{array} {r|r r } 0 & 0 & 0 \\ 1 & 1 & 0 \\ \hline & 1/2 & 2/2 \\ \end{array}$$Para aproximar la solución del PVI del enunciado en $t=0.4$, partiendo de $t_0=0$ e $y_0=0$ con paso $h=0.2$, siendo $f(t,y)=t+e^y$, hemos de realizar dos pasos.
f=@(t,y) t+exp(y)
%Valores
h=0.2;t0=0;y0=0;
%Paso 1
K1=f(t0,y0)
K2=f(t0+h/2,y0+h/2*K1)
K3=f(t0+3*h/4,y0+3*h/4*K2)
y1=y0+h/9*(2*K1+3*K2+4*K3)
%Paso 2
t1=t0+h;
K1=f(t1,y1)
K2=f(t1+h/2,y1+h/2*K1)
k3=f(t1+3*h/4,y1+3*h/4*K2)
y2=y1+h/9*(2*K1+3*K2+4*k3)
Escribimos el código Matlab para resolver el problema definiendo los valores $K_i$ correspondientes al tablero.
Modificamos el código para definir los valores $K_i$ a través de las matrices A,B y C que definen el tablero.
Utiliza el método de Runge-Kutta clásico para encontrar la solución con las condiciones iniciales siguientes $$y_1(0) = 1,\,\,y_2(0) =1,\,\,\, y_3(0) = 0,\,\,\,y_4(0) = 1$$
- la función mirkf4c.m para definir los parámetros del método de Runge-kutta clásico: a, b, c
- la función pasorkf.m para definir un paso del método con los parámetros: f, tn, hn, yn, a, b, c
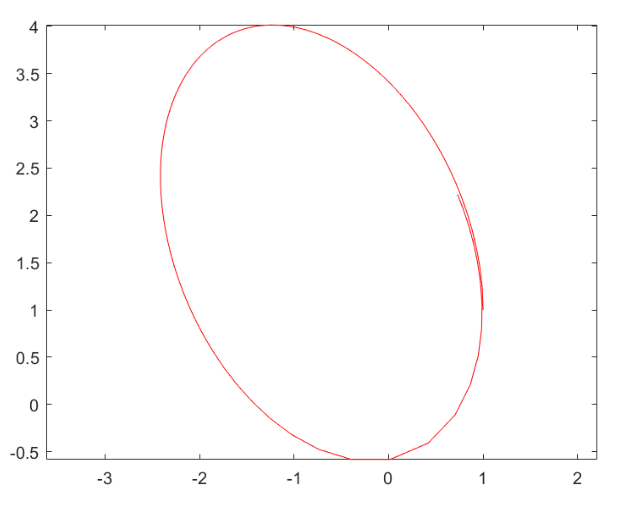
Nota: Ségún la primera ley de Kepler: ”los planetas describen ́orbitas eĺıpticas alrededor del sol, que ocupa uno de los focos de esa elipse”. En general, las soluciones del problema de dos cuerpos son cónicas (pueden ser elipses, paŕabolas o hiṕerbolas), pero si se toman las condiciones iniciales siguientes: $$y_1(0) = 1,\,\,y_2(0) = y_3(0) = 0,\,\,\,y_4(0) = 1$$ la solución es una circunferencia de centro el origen radio 1 y con periodo $2\pi$.
t0=0;tf=8*pi;
y0=[1;1;0;1];N=100;hn=tf/N;
%Definición de la función
f=@(t,y) [y(3);y(4);-y(1)/(y(1)^2+y(2)^2)^(3/2);-y(2)/(y(1)^2+y(2)^2)^(3/2)];
tn=t0;yn=y0;t=tn;y=yn;
[a,b,c]=mirkf4c; %Runge Kutta
for iter=1:N
[yn1]=pasorkf(f,tn,hn,yn,a,b,c);
tn=tn+hn;yn=yn1;
t=[t tn];y=[y yn];
end
%Representación de la solución
plot(y(1,:),y(2,:),'r')
axis equal
Sin utilizar la función pasorkf que calcula cada paso será:
Error de los métodos de Runge-Kutta
Veamos a continuación cómo analizar el error en los métodos de Runge-Kutta. Observemos en primer lugar que los métodos pueden escribirse de la forma $${y_{n + 1}} = {y_n} + {h_n}{\Phi _f}\left( {{t_n},{y_n},{h_n}} \right)\,\,\,\,\,\,\,0 \le n \le N - 1$$ Se definen a continuación dos tipos de errores.
- El error local es que se comete al dar un paso partiendo del conocimiento del valor exacto de la solución en el instante $t_n$.
- El error global es el que se comete al dar un paso a partir de la aproximación de ${y_n} \approx y(t_n)$.
Puede demostrarse que si el método es de orden $p$, entonces el error global es estimado por la siguiente calidad $$\left\| {{e _n}} \right\| \le {C \over A}\left[ {{e^{\left( {{t_n} - {t_o}} \right)}} - 1} \right]{h^p}\,\,\,\,\,\,\,\,\,\,\,h = \max {h_n}$$ y $A$ es la constante positiva que existe, al ser f derivable, cumpliendo $$\left\| {{\phi _f}\left( {t,y,h} \right) - {\phi _f}\left( {t,z,h} \right)} \right\| \le A\left\| {y - z} \right\|$$
Para obtener el orden de un método en términos de los coeficientes del mismo, Butcher, estableció las condiciones que se deberían cumplir. Tomando el vector de $m$ componentes $e=(1,1,...,1)^T$ se debe exigir a todos los métodos que $Ae=c$ y además, a continuación, se indican las condiciones que se deben cumplir para los tres primeros órdenes.
- Orden 1. $b^Te=1$
- Orden 2. La anterior más la condición $b^Tc=1/2$
- Orden 3. La anterior más la condición $b^Tc^2=1/3$, $b^TAc=1/6$
Métodos de Runge Kutta encajados
Los métodos vistos tipo no dejan de tener una dependencia directa del paso $h$ fijado inicialmente, por lo que su eleccíon puede condicionar enormemente el funcionamiento del propio ḿetodo. Nos planteamos entonces ćomo determinar cúal es el paso de tiempo h mas indicado. Con el fin de solventar este problema, comienzan a desarrollarse t́ecnicas para controlar esta “dependencia del paso de tiempo” de los ḿetodos, nacen así los métodos encajados.
Estos ḿetodos consisten en una variación del paso $h$ a partir del control de los errores de aproximacion obtenidos a medida que se calculan las diferentes iteraciones del ḿetodo. Así, si llegado el momento, el error de aproximación supera la tolerancia establecida para ́este, el método varía el paso para tener una mejor aproximacion. Por el contrario, si el error es menor que la tolerancia, el ḿetodo amplía el paso con el fin de acelerar el rendimiento.
El procedimiento entre los métodos de Runge-Kutta consiste en utilizar dos métodos distintos durante la integración $${y_{n + 1}} = {y_n} + {h_n}{\Phi _f}\left( {{t_n},{y_n},{h_n}} \right)\,\,\,\,\,\,\,\,\,\,orden\,\,p$$ $${\widehat y_{n + 1}} = {y_n} + {h_n}{\psi _f}\left( {{t_n},{y_n},{h_n}} \right)\,\,\,\,\,\,\,\,\,\,orden\,\,q > p$$ Los métodos eficientes que se utilizan tienen las matrices $A$ y $C$ del método de orden $p$ encajados en $\widehat A$ y $\widehat c$ de orden $q > p$.
Fehlberg construyó pares de métodos encajados de orden 4 y 5.
Runge-Kutta-Felhberg 4-5 #1 $$\begin{array} {r|r r r r r} 0 & & & & & \\ 2/9 & 2/9 & & & & \\ 1/3 & 1/12 & 1/4 & & & \\ 3/4 & 69/128 & -243/128 & 135/64 & & \\ 1 & -17/12 & 27/4 & -27/5 & 16/15 & \\ \hline orden \,\,4 & 1/9 & 0 & 9/20 & 16/45 & 1/12\\ \end{array}$$
$$\begin{array} {r|r r r r r} 0 & & & & & \\ 2/9 & 2/9 & & & & \\ 1/3 & 1/12 & 1/4 & & & \\ 3/4 & 69/128 & -243/128 & 135/64 & & \\ 1 & -17/12 & 27/4 & -27/5 & 16/15 & \\ 5/6 & 65/432 & -5/16 & 13/16 & 4/27 & 5/144 & \\ \hline orden \,\,5 & 47/450 & 0 & 12/25 & 32/225 & 1/30 & 6/25\\ \end{array}$$Se observa que los parametros $A$ y $c$ del ḿetodo de orden 4 son coincidentes con las 5 primeras filas de los paŕametros $\widehat A$ y $\widehat c$ del método de orden 5. Por lo tanto, los valores $K_{n,i}$ para $1 \le i \le 5$ son coincidentes para ambos metodos. Esto simplifica notablemente el numero de cálculos, particularmente el ńumero de evaluaciones de la función $f$.
Para pasar de $t_n$ a $t_{n+1}$ aplicamos el método de orden 5 para obtener $\widehat y_{n+1}$. Para hallar una cota del error local de aproximacion de $y(t_{n+1})$ se aplica el método de orden 4 para obtener $y_{n+1}$. Una estimación del error cometido es $$\left\| {{{\widehat y}_{n + 1}} - {y_{n+1}}} \right\|$$
Además, si $${y_{n + 1}} = {y_n} + {h_n}\sum\limits_{j = 1}^m {{b_j}{K_{n,j}}} $$ $${\widehat y_{n + 1}} = {y_n} + {h_n}\sum\limits_{j = 1}^{\widehat m} {{{\widehat b}_j}{K_{n,j}}} \,\,\,\,\,\,\,\,\,\,\,\widehat m > m$$se tiene que $$\left\| {{{\widehat y}_{n + 1}} - {y_{n+1}}} \right\| = {h_n}\sum\limits_{j = 1}^{\widehat m} {\left( {{{\widehat b}_j} - {b_j}} \right){K_{n,j}}} $$ por lo que basta conocer los parámetros del método de orden $q$ y los estimadores (${{{\widehat b}_j} - {b_j}})$ para calcular $$e_n=||{\widehat y_{n + 1}}-y_{n+1}||$$
La información que se precisa se incluye en el siguiente tablero.Runge-Kutta-Felhberg 4-5 #2
El siguiente tablero describe otro método Runge-Kutta-Fehlberg donde también se encajan también un método de orden 4 y otro de orden 5.
La tolerancia deseada se mide entre el error absoluto $e_a$ y el error relativo $e_r$. Dado que el error de $q$ es menor que el de $p$, se considera para la tolerancia el del método de orden $q$ $$TOL=e_a+e_r||{\hat y_{n + 1}}||$$
Con todo lo anterior, a partir de dos métodos encajados de órdenes $p$ y $q$ con $q <q$, utilizando los estimadores, $est$, el algoritmo que daría un paso de método es el siguiente
La función rkf.m implementa el algoritmo. Para ello necesita:
- f: nombre de la función que define la ecuación diferencial
- tn: el instante del que se parte
- hn: el paso que se va a dar
- yn: la aproximación de la solución conocida en el instante $t_n$
- a,b,c,est: los parámetros del algorítmo A,b,c y los estimadores
Esta función devuelve
- yn1: la aproximación de $y(t_{n+1})$ con $t_{n+1}=t_n+h_n$
- en: una estimación del error $e_n=||y(t_{n+1})-y_{n+1}||$
Antes de aceptar el valor obtenido, se debe comprobar si el error es menor que la tolerancia. Si es menor se acepta el paso y si es mayor se rechaza. En cualquier paso se debe proceder con la estrategia de control de paso siguiente:
Elección de $h_0$
$${h_o} = \max \left\{ {e_a + e_r{{\left\| {{y_o}} \right\|}^{{1 \over {p + 1}}}},{\rm{h_{min}}}} \right\}$$ donde podemos fijar por ejemplo $${h_{\min }} = {{{t_f} - {t_o}} \over {{{10}^6}}}$$
- Criterio de aceptación del paso. Se acepta si
$$e_n = \left\| {{{\hat y}_{n + 1}} - {y_{n + 1}}} \right\|{\rm{ < }}\,\,TOL = {e_a} + {e_r}||{\hat y_{n + 1}}||$$
- Reducción del paso tras un fallo. Si $e_n>TOL$ se debe reducir $h_n$ con un factor de reduccion $r_n<1$. Se considera $${r_n} = 0.9{\left( {{TOL} \over {e_{n}} } \right)^{{1 \over {p + 1}}}}$$ y como medida de seguridad se reducirá el paso al menos a la mitad, por lo que se considerará $${h_n} \to \min \left\{ {{r_n},{r_{\min }}} \right\}{h_n}$$ Se toma un valor entre 0.1 y 0.5, tomaremos $r_{min}=0.5$
Previsión del paso siguiente. Si ha habido un fallo del paso en la determinación de una de las dos últimas aproximaciones de la solución, entonces se toma $r_{max}=1$, en caso contrario se fija $r_{max}=5$.
Se calcula $r_n$ de la forma indicada en el punto 3 y se toma $${h_{n + 1}} = \left\{ \begin{aligned} & {h_n}\,\,si\,\,\,{r_n} \in \left[ {1,\,\,1.1} \right]\\ & \min \left\{ {{r_n},{r_{\max }}} \right\}\,\text{en otro caso} \end{aligned} \right.$$ En el caso de que el paso proporcione un error inferior a la tolerancia, tenemos que analizar la posibilidad de incrementar este paso para acelerar la integración. El factor de incremento del paso nunca será mayor que $r_{max}=5$, esto se hace para evitar fallos.
Problemas de contorno. Método de tiro
En este apartado vamos a estudiar el problema siguiente: $$\begin{aligned} & y''\left( t \right) = f\left( {t,y\left( t \right),y'\left( t \right)} \right)\,\,\,\,\,\,\,\,t \in \left[ {{t_o},{t_f}} \right] \cr & y\left( {{t_o}} \right) = {y_o}\,\,\,\,\,,\,\,\,\,y\left( {{t_f}} \right) = {y_f} \end{aligned}$$ En este caso no se puede aplicar el método de Runge-Kutta para integrar esta ecuación porque no tenemos $y'(t_0)$. Lo que haremos será resolver el siguiente problema: $$(P) \,\,\,\,\left\{ \begin{aligned} & y{'_1}\left( t \right) = {y_2}\left( t \right) \\ & y{'_2}\left( t \right) = f\left( {t,{y_1}\left( t \right),{y_2}\left( t \right)} \right)\,\,\,\,\,\,\,t \in \left[ {{t_o},{t_f}} \right] \\ & y_1\left( {{t_o}} \right) = {y_o}\,\,\,\,\,,\,\,\,\,y_2\left( {{t_o}} \right) = x \end{aligned} \right.$$ y buscar el valor de $x$ de forma que la solución $y_x=(y_{x,1},y_{x_2})^T$ cumpla que $y_{x,1}$ para el valor de $t=t_f$ sea $y_f$.- $e_a=10^{-14}$, $e_r=10^-12$.
- $f$ es el nombre del fichero .m que define a la función diferencial
- $t$ es el vector fila de instantes $t_n$ donde se ha calculado la aproximación de la solución de (P).
- $y$ es el vector solución que tiene dos filas $y_{x,1}$ para $y_1$ e $y_{x,2}$ para $y_2$.
f=....;
to=. . .;
yo=[y0;x];
tf=. . .;
ea=10^−14;
er=10^−12;
[tx,yx]=oderkf(f,to,yo,tf,ea,er);
%la condición es y(tf)=yf;
gx=yx(1,end)-yf;
end
Veamos el procedimiento en un ejemplo.
Paso 1. Definición de la ecuación diferencial en la función en el fichero odeEj.m
z=[y(2);1/t^3*(y(1)-t*y(2))^2];
Paso 2. Definición de la función $fe$ a la que aplicar el método de la secante.
f=
to=
tf=
yo=
ea=10^-14;
er=10^-12;
[tx yx]=oderkf(f,to,yo,tf,ea,er);
fx=
end
Paso 3. Aplicamos método de la secante a la función $fe(x)$ para hallar $x$ de forma que $fe(x)=0$.
El método puede adaptarse fácilmente al siguiente ejemplo.
Paso 1. Definición de la ecuación diferencial en la función en el fichero odeEj.m
z=[y(2);1/t^3*(y(1)-t*y(2))^2];
Paso 2. Definición de la función $fe$ a la que aplicar el método de la secante.
f=
to=
tf=
yo=
ea=10^-14;
er=10^-12;
[tx yx]=oderkf(f,to,yo,tf,ea,er);
fx=
end
Paso 3. Aplicamos método de la secante a la función $fe(x)$ para hallar $x$ de forma que $fe(x)=0$.
Paso 1. Definición de la ecuación diferencial en la función en el fichero ode.m
z=[y(2);t*y(1)^3-1-sin(t)];
Paso 2. Definición de la función $g$ a la que aplicar el método de la secante.
f=
to=
tf=
yo=
ea=10^-14;
er=10^-12;
[tx yx]=oderkf(f,to,yo,tf,ea,er);
fx=
end
Paso 3. Aplicamos método de la secante a la función $g(x)$ para hallar $x$ de forma que $g(x)=0$.
Consideramos $${y_1} = y,\,\,\,{y_2} = y',\,\,\,\,\,{y_3} = z,\,\,\,\,{y_4} = w$$ pudiendo escribirse $$\begin{aligned} &y'_1 = {y_2}\\ &y'_2 = sen\left( {{y_1}} \right) + 0.01\,\, t\,\, {y_1} + 0.1\,\, {y_3}\\ &y'_3\left( t \right) = sen\left( {{y_1} + {y_3}} \right) + {y_4}\\ &y'_4\left( t \right) = \cos \left( {{y_1} + {y_3} + {y_4}} \right)\\ &{y_1}\left( 0 \right) = 0 = {y_3}\left( 0 \right),\,\,\,\,\,{y_4}\left( 0 \right) = 1\,\,,\,\,\,\,\,\,{y_2}\left( 0 \right) = x \end{aligned}$$ y se buscará x para que $${y_{x,1}}\left( \pi \right) + {y_{x,3}}\pi + {y_{x,4}}\left( \pi \right) = 0$$
z=[y(2);sin(y(1))+0.01*t*y(1)+0.1*y(3);
sin(y(1)+y(3))+y(4);cos(y(1)+y(3)+y(4)]
end
Octave online
Octave es una alternativa a Matlab con un aspecto y unos comandos y sintasis similares. Se trata de un lenguaje interpretado de alto nivel. Lo puedes descargar desde su página oficial completamente gratis. Aquí tienes el enlace de descarga.
Pero además, puedes utilizar una versión en línea desde tu móvil en el caso de que no tengas a mano tu ordenador. Esta versión la tienes aquí: Octave online.
