Métodos numéricos
Libro interactivo

Métodos Numéricos

Elena E. Álvarez Saiz

Red Educativa Digital Descartes.
Universidad de Cantabria

Título de la obra:
MÉTODOS NUMÉRICOS


Autores:
Elena E. Alvarez Saiz



Diseño del libro: Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$


Primera Edición



LICENCIA

Creative Commons Attribution License 4.0.

Tabla de contenido

Capítulo IV

Integración numérica

Introducción

En este capítulo nos dedicaremos a encontrar una aproximación de la integral $\int\limits_a^b {f\left( x \right)dx} $ cuando $f$ es una función integrable en $[a,b]$. Analizaremos también el error que se comete en la aproximación y cómo obtener su valor con una precisión dada.

Este problema se plantea por varias razones:

  1. La posibilidad de aplicar la Regla de Barrow se restringe a una pequeña parte de funciones elementales que tienen primitivas también elementales. Muchas funciones, como por ejemplo $e^{x^2}$ que es continua, no tienen primitiva elemental.
  2. Aunque existiera un procedimiento para encontrar la primitiva, llegar a ella puede resultar en muchos casos tedioso. Pensemos por ejemplo en las funciones racionales o en aquellas que requieren de cambios de variable más o menos ingeniosos.
  3. Por otro lado, en muchas aplicaciones sólo se tiene una tabla de valores de la función $f$ o la posibilidad de obtener su valor en un número finito de puntos.

Estas razones obligan a encontrar métodos alternativos para calcular el valor de una integral definida en un intervalo de forma aproximada. Por razones históricas, el cálculo aproximado de integrales se denomina cuadratura dejando la denominación de integración para la resolución de ecuaciones diferenciales.

En cálculo I se vio una forma de aproximar el valor de la integral definida mediante sumas de Riemann.

Veremos en este tema otras fórmulas utilizando polinomios interpoladores.

Métodos habituales para obtener fórmulas de cuadratura

Si se considera un polinomio $p$ interpolador de $f$ en $n+1$ nodos, se tendría $$\left\{ {{x_i}} \right\}_{i = 0}^n \subset \left[ {a,b} \right]\,\,\,\,\,\,\,\,\,\,\,\,p\left( {{x_i}} \right) = f\left( {{x_i}} \right)\,\,i = 0,1,...,n$$

Una primera aproximación del valor de la integral de $f$ en $[a,b]$ podría ser $$\int\limits_a^b {f\left( x \right)dx} \approx \int\limits_a^b {p\left( x \right)dx} $$

Considerando el polinomio de interpolación de Lagrange, se tendrá que: $$p\left( x \right) = \sum\limits_{i = 0}^n {f\left( {{x_i}} \right){l_i}\left( x \right)} \,\,\,\, , \,\,\,\,\,\,\, {l_i}\left( x \right) = \prod\limits_{j = 0\,\,\,j \ne i}^n {{{x - {x_j}} \over {{x_i} - {x_j}}}} \,\,\,\,\,\, 0 \le i \le n$$

y, por lo tanto, $$\int\limits_a^b {p\left( x \right)dx} = \sum\limits_{i = 0}^n {f\left( {{x_i}} \right)\int\limits_a^b {{l_i}\left( x \right)dx} } = $$ $$ = \left( {b - a} \right)\sum\limits_{i = 0}^n {f\left( {{x_i}} \right)\underbrace {\left( {{1 \over {b - a}}\int\limits_a^b {{l_i}\left( x \right)dx} } \right)}_{{w_i}}} $$

La aproximación será $$\int\limits_a^b {f\left( x \right)dx} \approx \left( {b - a} \right)\sum\limits_{i = 0}^n {{w_i}f\left( {{x_i}} \right)} \,\,\,\,\,\,\,\,(I)$$ $${w_i} = {1 \over {b - a}}\int\limits_a^b {{l_i}\left( x \right)dx} $$

Este tipo de cuadratura se dice que es una fórmula interpolatoria. Los puntos ${w_i}$ se denominan pesos y los puntos ${x_i}$ son los nodos de la fórmula de cuadratura.

Ejemplo Consideremos la función $f(x)=e^{-x^2}$, el intervalo $[0,1]$ y los 4 nodos siguientes $x_0=0$, $x_1=1/3$, $x_2=2/3$ y $x_3=1$. Calculemos la fórmula de cuadratura.
Se tendrá $$\int\limits_0^1 {{e^{ - {x^2}}}dx} \approx {\omega _o}{e^0} + {\omega _1}{e^{ - 1/9}} + {\omega _2}{e^{ - 4/9}}+ {\omega _3}{e^{ - 1}}$$ donde $${w_0} = \int\limits_0^1 {{l_o}\left( x \right)dx} \,\,\,\,\,\,\,\,\,\,\,\,\,{l_o} = {{\left( {x - 1/3} \right)\left( {x - 2/3} \right)\left( {x - 1} \right)} \over {\left( { - 1/3} \right)\left( { - 2/3} \right)\left( { - 1} \right)}}$$ $${w_1} = \int\limits_0^1 {{l_1}\left( x \right)dx} \,\,\,\,\,\,\,\,\,\,\,\,\,{l_1} = {{\left( {x - 0} \right)\left( {x - 2/3} \right)\left( {x - 1} \right)} \over {1/3 \cdot \left( { - 1/3} \right)\left( { - 2/3} \right)}}$$
$${w_2} = \int\limits_0^1 {{l_2}\left( x \right)dx} \,\,\,\,\,\,\,\,\,\,\,{l_2} = {{\left( {x - 0} \right)\left( {x - 1/3} \right)\left( {x - 1} \right)} \over {2/3 \cdot \left( { 1/3} \right)\left( { - 1/3} \right)}}$$ $${w_3} = \int\limits_0^1 {{l_3}\left( x \right)dx} \,\,\,\,\,\,\,\,\,\,\,{l_3} = {{\left( {x - 0} \right)\left( {x - 1/3} \right)\left( {x - 2/3} \right)} \over {1 \cdot \left( { 2/3} \right)\left( { 1/3} \right)}}$$ Se obtendría $${w_o} = {1 \over 8}\,\,\,\,\,\,\,{w_1} = {3 \over 8}\,\,\,\,\,\,\,\,{w_2} = {3 \over 8}\,\,\,\,\,\,{w_3} = {3 \over 8}$$ y,por tanto, $$\int\limits_0^1 {{e^{ - {x^2}}}dx} \approx {1 \over 8}{e^0} + {3 \over 8}{e^{ - 1/9}} + {3 \over 8}{e^{ - 4/9}} + {1 \over 8}{e^{ - 1}}$$

Vamos a ver en este tema cómo obtener estos pesos de forma más sencilla.

Ejemplo: La fórmula $\int\limits_0^2 {f\left( x \right)dx} \approx 3f\left( 0 \right) + f\left( 2 \right)$ no es de tipo interpolatorio.
En efecto, ya que $$\int\limits_0^2 {{l_o}\left( x \right)dx} = \int\limits_0^2 {{{x - {x_1}} \over {{x_o} - {x_1}}}\,} dx = \int\limits_0^2 {{{x - 2} \over {0 - 2}}\,} dx = 1 \ne 3$$
Esta tipo de fórmulas son eficientes en intervalos de longitud pequeña. Cuando el intervalo es de longitud grande, se descompone en subintervalos pequeños y se aplica en cada uno de ellos fórmulas de cuadratura.

Para ello se divide el intervalo $[a,b]$ en $k$ subintervalos $$a = {\alpha _o} < {\alpha _1} < ... < {\alpha _n} = b$$ obteniendo la siguiente aproximación $$\int\limits_a^b {f\left( x \right)dx} = \sum\limits_{i = 1}^k {\int\limits_{{\alpha _{i - 1}}}^{{\alpha _i}} {f\left( x \right)dx} } $$

Posteriormente se aplica la fórmula de cuadratura a cada subintervalo. Este tipo de fórmulas se denominan de cuadratura compuesta y se analizan en el apartado 1.4.

Para calcular la calidad de una fórmula de cuadratura se define su grado de precisión o exactitud.

DEFINICIÓN: Una fórmula de cuadratura tiene grado de exactitud $n\gt0$ si calcula exactamente la integral para cada polinomio de grado menor o igual que $n$, pero no es exacta para el menos un polinomio de grado $n+1$. Esto significa que para cada polinomio $q$ de grado menor o igual a $n$, se cumple $$\int\limits_a^b {q\left( x \right)dx} = \left( {b - a} \right)\sum\limits_{i = 0}^n {{\omega _i}\,q\left( {{x_i}} \right)} $$
TEOREMA. Si la fórmula de cuadratura $$\int\limits_a^b {f\left( x \right)dx} \approx \left( {b - a} \right)\sum\limits_{i = 0}^n {{w_i}f\left( {{x_i}} \right)} $$ es de tipo interpolatorio si y solo sí es exacta de grado $n$.

Ejemplo: Comprobar que la fórmula $$\int\limits_0^4 {f\left( x \right)dx} \approx 2f\left( 1 \right) + 2f\left( 3 \right)$$ es de tipo interpolatorio.
Se puede comprobar que es exacta para $f(x)=1$, $$\int\limits_0^4 {1\,dx} = 2 + 2$$ Es exacta para $f(x)=x$ $$\int\limits_0^4 {x\,dx} = 2 + 2 \cdot 3$$ Se puede ver además que el grado de precisión es exactamente uno ya que la fórmula no es exacta para $f(x)=x^2$ ya que $$\int\limits_0^4 {{x^2}\,dx} = {{64} \over 3} \ne 2 \cdot {1^2} + 2 \cdot {3^2} = 20$$

Veremos en primer lugar cómo obtener fórmulas de cuadratura elementales y el error asociado limitándonos a las fórmulas de Newton-Cotes. Posteriormente veremos cómo construir fórmulas de cuadratura compuesta para aproximar la integral con un error inferior a la precisión dada.

Fórmulas de cuadratura de Newton-Cotes

Estas fórmulas de cuadratura son de tipo interpolatorio $$\int\limits_a^b {f\left( x \right)dx} \approx \left( {b - a} \right)\sum\limits_{i = 0}^n {{w_i}f\left( {{x_i}} \right)} \,\,\,\,\,\,\,\,\,\,\,\,\,{w_i} = {1 \over {b - a}}\int\limits_a^b {{l_i}\left( x \right)dx} $$ donde los nodos se toman equidistantes.

DEFINICIÓN. Se llama fórmula de Newton-Cotes (también fórmula cerrada de Newton-Cotes) a aquella fórmula de cuadratura numérica de tipo interpolatorio, donde los nodos vienen dados por la expresión $${x_j} = a + jh\,\,\,,\,\,\,0 \le j \le n\,\,\,\,\,,\,\,\,h = {{b - a} \over n}$$ Es decir, se tienen $n+1$ nodos equidistantes $$a = {x_o} < {x_1} < {x_2} < ... < {x_n} = b$$ $$h = {x_j} - {x_{j - 1}}\,\,\,\,\,\,j = 1,...,n$$

En la práctica resulta de utilidad el siguiente resultado.

Los pesos son independientes del intervalo siempre que se elijan adecuadamente los nodos, esto es, estén relacionados por la transformación de $[a,b]$ en $[c,d]$ dada de la siguiente forma, $$\begin{aligned} & \left[ {a,b} \right] &\to &\left[ c,d \right] \\ & x &\to & t = c + {{d - c} \over {b - a}}\left( {x - a} \right) \end{aligned}$$
Este resultado significa que si se cambia de intervalo $[a,b]$ a $[c,d]$ y se consideran los nodos $x_i$ en $[a,b]$ y $t_i$ en $[c,d]$ relacionados de la forma siguiente: $${t_i} = c + {{d - c} \over {b - a}}\left( {{x_i} - a} \right)$$ se tendrá que los pesos en ambos casos coinciden $$\widehat {{\omega _i}} = {1 \over {d - c}}\int\limits_c^d {\widehat {{l_i}}\left( t \right)dt} = {1 \over {b - a}}\int\limits_a^b {{l_i}\left( x \right)dx} = {\omega _i}$$ donde $$\widehat {{l_i}} \left( t \right) = \prod\limits_{j = 0\,\,\,j \ne i}^n {{{t - {t_j}} \over {{t_i} - {t_j}}}} \,\,\,\,\,\, 0 \le i \le n$$ $${l_i}\left( x \right) = \prod\limits_{j = 0\,\,\,j \ne i}^n {{{x - {x_j}} \over {{x_i} - {x_j}}}} \,\,\,\,\,\, 0 \le i \le n$$

Con los resultados expuestos anteriormente vamos a ver que la construcción de las fórmulas de Newton-Cotes no precisa calcular los polinomios base de Lagrange y luego realizar las integrales para obtener los correspondientes pesos.

En efecto, sabiendo que la fórmula de cuadratura es exacta para todos los polinomios de grado menor o igual a $n$, dados los nodos $x_i$ para $i=0,1,...,n$ se pueden determinar los pesos formando un sistema de $n+1$ ecuaciones con $n+1$ incógnitas considerando las siguientes $n+1$ igualdades: $$\int\limits_a^b {{x^k}dx} = \left( {b - a} \right)\sum\limits_{j = 0}^n {{\omega _j}x_j^k} \,\,\,\,\,\,\,k = 0,1,...,n$$ Este sistema tiene una única solución ya que la matriz de coeficientes es de Vandermonde.

Veamos cómo aplicar estos resultados para calcular las primeras fórmulas de Newton-Cotes.

Primera fórmula de Newton-Cotes (n=1)

Consideramos dos nodos en el intervalo $[a,b]$, esto es, $x_0=a$ y $x_1=b$. La fórmula de cuadratura es $$\int\limits_a^b {f\left( x \right)dx} \approx \left( {b - a} \right)\left[ {{\omega _o}f\left( a \right) + {\omega _1}f\left( b \right)} \right]$$

Para calcular los pesos se considera el intervalo $[0,1]$ y se resuelve el sistema $$\begin{aligned} & k = 0\,\,\,\,\,\,\,\,\,&1 = \int\limits_0^1 {dx} = {\omega _o} + {\omega _1} \\ & k = 1\,\,\,\,\,\,\,\,\,&{1 \over 2} = \int\limits_0^1 {xdx} = {\omega _1} \end{aligned}$$

La solución del sistema es ${\omega _o} = {\omega _1} = {1 \over 2}$. Por lo tanto, $$\int\limits_a^b {f\left( x \right)dx} \approx {{b - a} \over 2}\left[ {f\left( a \right) + f\left( b \right)} \right]$$ Esta fórmula de Newton-Cotes de dos puntos se llama fórmula del trapecio.


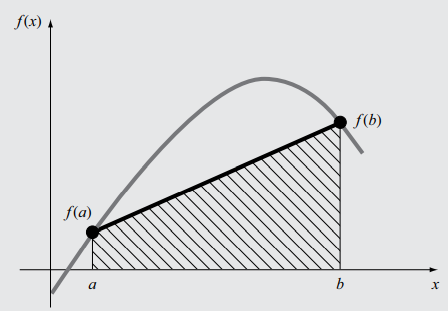
Segunda fórmula de Newton-Cotes (n=2)

En este caso el número de nodos es 3: $x_o=a$, $x_1=\frac{a+b}{2}$ y $x_2=b$. La fórmula de cuadratura en este caso es $$\int\limits_a^b {f\left( x \right)dx} \approx \left( {b - a} \right)\left[ {{\omega _o}f\left( a \right) + {\omega _1}f\left( {{{a + b} \over 2}} \right) + {\omega _2}f\left( b \right)} \right]$$ Para determinar los nodos consideramos el intervalo $[-1,1]$. Resolviendo el sistema de 3 ecuaciones con 3 incógnicas, obtenemos ${\omega _o} = {\omega _2} = {1 \over 6}$, ${\omega _1} = {2 \over 3}$. Por lo tanto: $$\int\limits_a^b {f\left( x \right)dx} \approx {{\left( {b - a} \right)} \over 6}\left[ {f\left( a \right) + 4f\left( {{{a + b} \over 2}} \right) + f\left( b \right)} \right]$$

Esta regla se llama regla de Simpson.

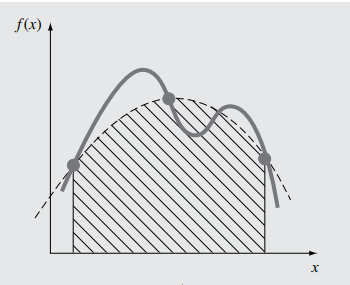
Fórmula de Newton-Cotes con n=3

En este caso el número de nodos es 4: $x_0=a$, $x_1=a+\frac{b-a}{3}$, $x_2=a+2 \frac{b-a}{3}$ y $x_3=b$. La fórmula de cuadratura es $$\int\limits_a^b {f\left( x \right)dx} \approx \left( {b - a} \right)\left[ {{\omega _o}f\left( a \right) + {\omega _1}f\left( { {{2a+b} \over 3}} \right) + } \right.{\rm{ }}$$ $$\left. +{{\omega _2}f\left( {{{a+2b} \over 3}} \right) + {\omega _3}f\left( b \right)} \right]$$ Para determinar los nodos consideramos el intervalo $[0,3]$ y se resuelve el sistema de 4 ecuaciones con 4 incógnitas asociado, obteniendo ${\omega _o} = {\omega _3} = {1 \over 8}$, ${\omega _1} = {\omega _2} = {3 \over 8}$ Por lo tanto: $$\int\limits_a^b {f\left( x \right)dx} \approx $$ $$ \approx {{\left( {b - a} \right)} \over 8}\left[ {f\left( a \right) + 3f\left( {{{2a + b} \over 3}} \right) + 3f\left( {{{a + 2b} \over 3}} \right) + f\left( b \right)} \right] $$ Esta fórmula se llama regla de los tres octavos.

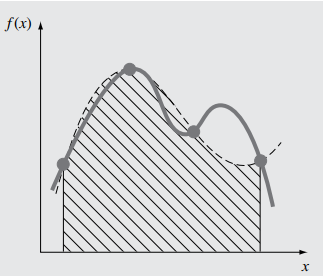
Notar que los pesos son simétricos, es decir, el primero es igual al último, el segundo es igual al penúltimo, etc.

De forma análoga pueden obtenerse las siguientes fórmulas de Newton-Cotes.

Ejemplo Obtener con Matlab la aproximación de la integral $\int\limits_0^\pi {{e^{senx\,\,\cos x}}dx} $ utilizando la regla de los tres octavos ($n=3$) y la de Hardy ($n=6$).

Error en la fórmula de cuadratura de Newton-Cotes.

Vamos a analizar en este apartado el error de las fórmulas de cuadratura de Newton-Cotes. El error de la aproximación es la diferencia entre el valor exacto y el aproximado, es decir: $$E = \int\limits_a^b {f\left( x \right)dx} - \left( {b - a} \right)\sum\limits_{j = 0}^n {{\omega _j}f\left( {{x_j}} \right)} $$ El siguiente resultado nos da una expresión para este error.

TEOREMA. Si $n$ es impar y la función $f$ es $n+1$ veces derivable y $f^{(n+1}$ es continua entonces existe $\xi \in \left[ {a,b} \right]$, de forma que el error de la fórmula viene dada por $$E = {{{h^{n + 2}}} \over {\left( {n + 1} \right)!}}{f^{(n + 1}}\left( \xi \right)\int\limits_0^n { \pi \left( x \right)} \,dx$$ donde $h=\frac{b-a}{n}$ y $\pi \left( x \right) = \left( x \right)\left( {x - 1} \right)...\left( {x - n} \right)$ Si $n$ es par y la función $f$ es $n+2$ veces derivable y $f^{(n+2}$ es continua entonces existe $\xi \in \left[ {a,b} \right]$, de forma que el error de la fórmula viene dada por $$E = {{{h^{n + 3}}} \over {\left( {n + 2} \right)!}}{f^{(n + 2}}\left( \xi \right)\int\limits_0^n {x\pi \left( x \right)} \,dx$$
Según este teorema, si $n$ es par, entonces el grado de precisión de la fórmula de Newton-Cotes es $n+1$. Cuando $n$ es impar, el grado de precisión es $n$.
Este teorema se puede escribir de la siguiente manera: $$E = \left\{ \begin{aligned} &{C_n}{h^{n + 2}}{f^{(n + 1}}\left( \xi \right)\,\,\,\,\,\text{si n impar} \\ &{C_n}{h^{n + 3}}{f^{(n + 2}}\left( \xi \right)\,\,\,\,\,\text{si\ n par} \end{aligned} \right. $$ donde la constante $C_n$ tiene el siguiente valor: $$C_n = \left\{ \begin{aligned} &{1 \over {\left( {n + 1} \right)!}}\int\limits_0^n {t \left( {t - 1} \right)\left( {t - 2} \right)} ...\left( {t - n} \right)dt \,\,\,\,\,\text{si n impar} \\ & {1 \over {\left( {n + 2} \right)!}}\int\limits_0^n {t^2 \left( {t - 1} \right)\left( {t - 2} \right)} ...\left( {t - n} \right)dt \,\,\,\,\,\text{si n par} \end{aligned} \right. $$
El error de la fórmula de cuadratura de Newton Cotes se puede escribir de la forma siguiente: $$E = {C_n}{h^{m + 1}}{f^{(m}}\left( \xi \right)$$ siendo $m = \left\{ \begin{aligned} &n + 1\,\,si\,\,n\,\,impar \\ &n + 2\,\,si\,\,n\,\,par \\ \end{aligned} \right.$, $C_n$ una constante que viene dada por la expresión anterior y $\xi \in \left[ {a,b} \right]$.
Vamos a determinar el valor de las constantes $C_n$ para las primeras fórmulas de Newton-Cotes.

Error en la fórmula del trapecio ($n=1$)

Consideremos la fórmula de Newton-Cotes para $n=1$, que es impar. Tomamos $m=n+1=2$. Se tiene que $$\begin{aligned} E=&\color{red}{\int\limits_a^b {f\left( x \right)dx}} \color{black}{-} \color{green}{{{b - a} \over 2}\left( {f\left( a \right) + f\left( b \right)} \right)} \\ E=&{C_1} h^3 f''\left( \xi \right) \end{aligned}$$ Para determinar $C_1$, consideramos la función $f(x)=(x-a)^m=(x-a)^2$. Para esta función se tiene que por un lado se cumple $$\color{red}{\int\limits_a^b {f(x)dx}} \color{black}{=\int\limits_a^b {{(x-a)^2}dx} = {1 \over 3}{\left( {b - a} \right)^3} =} \color{red}{{ {h^3} \over 3}}$$ y por otro $$\color{green}{{{b - a} \over 2}\left( {f\left( a \right) + f\left( b \right)} \right)} \color{black}{= {{b - a} \over 2}\left( {0 + {{\left( {b - a} \right)}^2}} \right) =} {{{{\left( {b - a} \right)}^3}} \over 2} = \color{green}{ \frac {h^3} {2}}$$ Por lo tanto, $${C_1}{h^3}{f^{''}}\left( \xi \right) = {{{h^3}} \over 3} - {{h^3} \over 2}$$es decir, $$2 {C_1} = {1 \over 3} - {1 \over 2} = - {1 \over 6}$$ $${C_1} = - {1 \over 12}$$

Se cumple entonces $$\int\limits_a^b {f\left( x \right)dx = {{b - a} \over 2}\left[ {f\left( a \right) + f\left( b \right)} \right]} - {1 \over {12}}{h^3}{f^{''}}\left( \xi \right)$$ para algún valor de $\xi$ en $[a,b]$.

Error en la fórmula de Simpson

Consideremos la fórmula de Newton-Cotes para $n=2$ que es par, consideramos $m=n+2=4$. Se tiene que $$\begin{aligned} E=&\int\limits_a^b {f\left( x \right)dx} - {{{b - a} \over 6}\left[ {f\left( a \right) + 4f\left( {{{a + b} \over 2}} \right) + f\left( b \right)} \right]} \\ E=&{C_2} h^5 f''\left( \xi \right) \end{aligned}$$ Para determinar $C_2$ consideramos la función $f(x)=(x-a)^m=(x-a)^4 $. Se tiene que por un lado se cumple $$\int\limits_a^b {{(x-a)^4}dx} = {1 \over 5}{\left( {b - a} \right)^5} = { {(2h)^5} \over 5}$$ y por otro $${{b - a} \over 6}\left[ {0 + 4\, \cdot {h^4} + {(2h)^4}} \right] = {{2h^5} \over 6} \cdot 20$$

Por lo tanto, $${C_2}{h^5}{f^{iv}}\left( \xi \right) = {{{2^5 h^5}} \over 5} - {{20 h^5} \over 3}$$ es decir, $$4!{C_2} = {{{2^5}} \over 5} - {{20} \over 3} = - {4 \over {15}}\,\,\,\,\,\,\, \Rightarrow \,\,\,\,\,\,{C_2} = - {1 \over {90}}$$
Se cumple entonces $$\int\limits_a^b {f\left( x \right)dx = {{b - a} \over 6}\left[ {f\left( a \right) + 4f\left( {{{a + b} \over 2}} \right) + f\left( b \right)} \right]} + E$$ $$E = - {1 \over {90}}{h^5}{f^{(iv}}\left( \xi \right)$$ para algún valor de $\xi$ en $[a,b]$.

Error en la fórmula de cuadratura 3/8

Consideremos la fórmula de Newton-Cotes para $n=3$, que es impar. Tomamos $m=n+1=4$. Se tiene que $$E=\int\limits_a^b {f\left( x \right)dx} - $$ $${{\left( {b - a} \right)} \over 8}\left[ {f\left( a \right) + 3f\left( {{{2a + b} \over 3}} \right) + 3f\left( {{{a + 2b} \over 3}} \right) + f\left( b \right)} \right] $$

$$E={C_3} h^5 f^{(4}\left( \xi \right)$$

Para determinar $C_3$ se considera la función $f(x)=(x-a)^m=(x-a)^4$. Se cumplirá $$\int\limits_a^b {{(x-a)^4}dx} = {1 \over 5}{\left( {b - a} \right)^5} = { {(3h)^5} \over 5}$$ $${{3h} \over 8}\left[ 0 + 3\, \cdot {h^4} + 3\, \cdot (2h)^4 + (3h)^4 \right] = {{99h^5} \over 2} $$ Por lo tanto, $$E={C_3} h^5 f^{(4}\left( \xi \right)=\frac{-9}{10}h^5$$ $$4!{C_3} = {{ - 9} \over {10}}\,\,\,\,\,\, \Rightarrow \,\,\,{C_3} = - {3 \over {80}}$$

Se cumple $$\int\limits_a^b {f\left( x \right)dx} = $$ $${{\left( {b - a} \right)} \over 8}\left[ {f\left( a \right) + 3f\left( {{{2a + b} \over 3}} \right) + 3f\left( {{{a + 2b} \over 3}} \right) + f\left( b \right)} \right] + E$$ $$ E=-\frac{3}{80} h^5 f^{(4}\left( \xi \right)$$ para algún valor de $\xi$ en $[a,b]$.

En la siguiente imagen se muestra la expresión del resto para cada una de las fórmulas de Newton-Cotes vistas anteriormente.

Ejemplo Considerar la integral $\int\limits_0^\pi {{e^{sen\left( x \right)}}dx} $ usando la regla del trapecio.
En este caso $f(x)=e^{sen(x)}$, la aproximación es $$\int\limits_0^\pi {{e^{sen\left( x \right)}}dx} \approx {\pi \over 2}\left[ {f\left( 0 \right) + f\left( \pi \right)} \right] = {\pi \over 2}\left[ {{e^{sen0}} + {e^{sen\pi }}} \right] = \pi $$
El error de la fórmula de los trapecios $$E = \color{red}{\int\limits_a^b {f\left( x \right)dx} } - \color{green}{{\rm{ }}{{\left( {b - a} \right)} \over 2}\left[ {f\left( a \right) + f\left( b \right)} \right]}\color{black}{ = - {{{{\left( {b - a} \right)}^3}} \over {12}}{f^{''}}\left( \xi \right)}$$ con $\xi \in \left[ {a,b} \right]$. En este caso $$E = \color{red}{\int\limits_0^\pi {{e^{sen\left( x \right)}}dx}} -\color{green}{ {{\pi} \over 2}\left[ {f\left( 0 \right) + f\left( {\pi} \right)} \right] }\color{black}{= - {{{\pi ^3}} \over {12}}{f^{''}}\left( \xi \right){\rm{ }}\,\,\,\,\xi \in \left[ {0,\pi } \right]}$$ Dado que $$f'\left( x \right) = \cos \left( x \right){e^{sen\left( x \right)}}{\rm{ }}$$$$ f''\left( x \right) = {\cos ^2}\left( x \right){e^{sen\left( x \right)}} - sen\left( x \right){e^{sen\left( x \right)}}$$ se tiene que $$\left| {f''\left( x \right)} \right| \le 2e$$ Una cota del error es, por tanto, $$\left| E \right| = \left| { - {{{\pi ^3}} \over {12}}{f^{''}}\left( \xi \right)} \right| \le {{{\pi ^3}e} \over 6}$$

Vemos que, en el caso de la fórmula de los trapecios, el error que se comete en la aproximación depende del cubo de la longitud del intervalo. Si se disminuye esta longitud, el error disminuye rápidamente. Eso se puede lograr dividiendo el intervalo en subintervalos, y aplicando la cuadratura a cada uno de ellos y sumando después los resultados obtenidos.

Fórmulas compuestas. Métodos adaptativos

Cuando la distancia entre los nodos $h$ es de longitud grande, mayor que 1, el error que se comete puede ser grande. Por ello, cuando el intervalo $[a,b]$ es grande se divide el intervalo $[a,b]$ en $N$ subintervalos $$a = {\alpha _o} < {\alpha _1} < ... < {\alpha _N} = b$$ y se calcula $$\int\limits_a^b {f\left( x \right)dx} = \sum\limits_{i = 1}^N {\int\limits_{{\alpha _{i - 1}}}^{{\alpha _i}} {f\left( x \right)dx} } $$ aplicando la fórmula de cuadratura a cada uno de los subintervalos $[{\alpha _{i-1}},{\alpha _i}]$.

Por ejemplo, la cuadratura del trapecio compuesta consiste en aproximar una integral en $[a,b]$ utilizando $N$ trapecios. En primer lugar, se divide el intervalo en $N$ subintervalos de longitud $h=\frac{b-a}{N}$. Despues de aplicar en cada uno de ellos la fórmula de cuadratura de los trapecios se obtiene $$\int_{a}^{b}fx)dx \approx \frac{h}{2} \left [ f(a)+2f(a+h)+2f(a+2h)+...+f(b) \right ]$$ El error en esta aproximación se corresponde con $$-\frac{(b-a)^3}{12N^2}f''(\xi ) \,\,\,\,\, \xi\epsilon (a,b)$$ siendo $N$ el número de subintervalos.
La cuadratura de Simpson compuesta consiste en aproximar una integral en $[a,b]$ dividiendo el intervalo en $N$ subintervalos de longitud $h=\frac{b-a}{N}$ y aplicar en cada uno de ellos la regla de Simpson. En este caso se precisarían $2N+1$ nodos $x_i=a+ih/2, \,\,0 \le i \le 2N$ se obtiene $$\int_{a}^{b}f(x)dx \approx \frac{h}{6} [ f(x_0)+4f(x_1)+2f(x_2)+4f(x_3)+...$$ $$...+4f(x_{2N-1})+f(x_{2N}) ]$$ El error en esta aproximación es $$ - {\left( {{{b - a} \over {2N}}} \right)^5}{N \over {90}}{f^{(4}}(\xi ) = - {\rm{ }}{{{{\left( {b - a} \right)}^5}} \over {180 \cdot {{(2N)}^4}}}{f^{(4}}(\xi ) \,\,\,\,\,\,\,\,\,\,\xi \in (a,b)$$
Ejemplo: Calcular la siguiente integral $$\int\limits_0^1 {\left( {1 + sen\left( {{x^2}} \right)} \right)\,dx} $$ utilizando la cuadratura de los trapecios compuesta dividiendo el intervalo en 4 subintervalos.
Observa que los métodos compuestos no tienen en cuenta las zonas de mayor variabilidad de la función ya que se considera la longitud de cada subintervalo siempre igual.

Dependiendo de la función, puede ser conveniente utilizando subintervalos más pequeños donde haya más variabilidad de la función. En estos métodos adaptativos se estima el error cometido en cada intervalo de forma que permita decidir si hay que subdividir el intervalo.
Cuadratura adaptiva trapecios

Se calcula la aproximación $I_1$ de la integral de $f$ en $[a,b]$ mediante la cuadratura de los trapecios en el intervalo $[a,b]$.

Por otro lado, se considera $I_2$ la aproximación de la integral utilizando la regla del trapecio compuesta con $N=2$ siendo $ \color{red}{E}$ el error de esta aproximación.

Se tendrá:

$$\int\limits_a^b {f\left( x \right)dx} = I_1 - {\color{blue}{\frac{(b-a)^3}{12} f''(\xi _1)}}$$ $$\int\limits_a^b {f\left( x \right)dx} = I_2 {\color{red}{-\frac{(b-a)^3}{12 \cdot 4} f''(\xi _2)}}=I_2+ {\color{red}{E}}$$ Si suponemos que $f''(\xi _1)\approx f''(\xi _2)$, restando las dos expresiones anteriores, podemos considerar que una estimación del error utilizando el método de los trapecios en dos subintervalos $$\left|I_2-I_1\right| \approx \left | \color{red}{E}-\color{blue}{4E} \right|= \left |3E\right|$$ $$\color{red}{\left |E\right|=\left |\int\limits_a^b {f\left( x \right)dx} - I_2\right|\approx \left |\frac{1}{3}(I_2-I_1)\right|}$$
Una estimación del error considerando como valor de la integral el valor de $I_1$ es decir, utilizando la cuadratura de los trapecios en el intervalo $[a,b]$, es $\color{blue}{\left |\frac{4}{3}(I_2-I_1)\right|}$.

Teniendo en cuenta la estimación anterior del error, el método recursivo para calcular la integral consiste en aplicar lo siguiente,

  • Si la estimación del error es menor que la tolerancia, devolvemos el valor de $I_2$ con la estimación del error.
  • Si esta estimación del error es mayor que la tolerancia, repetimos el proceso en cada subintervalo $[a, \frac{a+b}{2}$ y $[\frac{a+b}{2},b]$ permitiendo en cada subintervalo solo la mitad de la tolerancia.
Ejemplo: Calcular $$\int\limits_0^1 {\left( {1 + sen\left( {{x^2}} \right)} \right)\,dx} $$ utilizando la cuadratura de los trapecios adaptativa con un error menor que $10^{-5}$.
Cuadratura adaptiva Simpson

Llamando $I_1$ a la fórmula de cuadratura de Simpson en $[a,b]$ y llamando $I_2$ a la fórmula de cuadratura de Simpson compuesta con $N=2$, se tendrá, llamando $h=(b-a)/2$

$$\int\limits_a^b {f\left( x \right)dx} = I_1 -{\color{blue}{ \frac{h^5}{90 } f''(\xi _1)}}$$ $$\int\limits_a^b {f\left( x \right)dx} = I_2 - {\color{red}{\frac{h^5}{90 \cdot 2^4 } f''(\xi _2)}}=I_2+\color{red}{E}$$ Si suponemos que $f''(\xi _1)\approx f''(\xi _2)$, restando las dos expresiones anteriores, podemos considerar que una estimación del error utilizando el método de Simpson en dos subintervalos $$\left|I_2-I_1\right| \approx \left |E-16E \right|= \left |15E\right|$$
$$\color{red}{\left |E\right|=\left |\int\limits_a^b {f\left( x \right)dx} - I_2\right|\approx \left |\frac{1}{15}(I_2-I_1)\right|}$$
Una estimación del error utilizando Simpson en un intervalo $[a,b]$ es, por tanto, $\color{blue}{\left |\frac{16}{15}(I_2-I_1)\right|}$.

Teniendo en cuenta la estimación anterior del error, el método recursivo para calcular la integral consiste en aplicar lo siguiente,

  • Si esta estimación del error es menor que la tolerancia, devolvemos el valor de $I_2$ con la estimación del error.
  • Si esta estimación del error es mayor que la tolerancia, repetimos el proceso en cada subintervalo $[a, \frac{a+b}{2}$ y $[(\frac{a+b}{2},b]$ permitiendo en cada subintervalo solo la mitad de la tolerancia.
Ejemplo: Calcular $$\int\limits_0^1 {\left( {1 + sen\left( {{x^2}} \right)} \right)\,dx} $$ utilizando el método de Simpson adaptativo con un error menor que $10^{-5}$.

Ejercicio Calcular la siguiente integral $\int\limits_0^\pi {{e^{{\rm{sen}}x\cos x}}\,dx} \,$ con un error inferior a $10^{-12}$.

Solución: 3.341031544735790

Ejercicio Calcular la siguiente integral $\int\limits_0^4 {{e^{ - {x^2}}}dx} $ con un error inferior a $10^{-12}$.

Solución: 0.886226911789732

Ejercicio Calcular la siguiente integral $\int\limits_0^4 {{e^{{x^2}}}dx} $ con un error inferior a $10^{-6}$.

Solución: 1.149400634590278e+06

Veamos cómo encontrar una estimación del error cuando se utiliza una fórmula de Newton-Cotes considerando dos pasos diferentes $h$ y $h/2$ y una estrategia para aplicar este método adaptativo en general.

Cuadratura adaptiva

Si llamamos $I$ a la aproximación de la integral $$\int\limits_a^b {f\left( x \right)dx} = I + E \,\,\, \text{con} \,\,E = {C_n}{h^{m + 1}}{f^{(m}}\left( \xi \right)$$ siendo $$m = \left\{ \begin{aligned} &n + 1\,\,si\,\,n\,\,impar \\ &n + 2\,\,si\,\,n\,\,par \\ \end{aligned} \right.$$

Aplicando la misma fórmula a los intervalos $[a,\frac{a+b}{2}]$ y $[\frac{a+b}{2},b]$ se tendrá, $$\begin{aligned} \int\limits_a^{\frac {a+b}{2}} {f\left( x \right)dx} &= {I_1} + {E_1} = {I_1} + {C_n}{\left( {{h \over 2}} \right)^{m + 1}}{f^{(m}}\left( {{\xi _1}} \right)\\ & {\xi _1} \in \left[ {a,{{a + b} \over 2}} \right] \end{aligned}$$ $$\begin{aligned} \int\limits_{{{a + b} \over 2}}^b {f\left( x \right)dx} &= {I_2} + {E_2} = {I_2} + {C_n}{\left( {{h \over 2}} \right)^{m + 1}}{f^{(m}}\left( {{\xi _2}} \right)\\ &{\xi _2} \in \left[ {{{a + b} \over 2},b} \right] \end{aligned}$$

Si $[a,b]$ es pequeño, $$I + E{\mkern 1mu} {\mkern 1mu} = {I_1} + {I_2} + {C_n}{{{h^{m + 1}}} \over {{2^m}}}\left[ {{{{f^{(m}}\left( {{\xi _1}} \right) + {f^{(m}}\left( {{\xi _2}} \right)} \over 2}} \right]$$ dado que el intervalo es pequeño, $$I + E{\mkern 1mu} {\mkern 1mu} \approx {I_1} + {I_2} + \underbrace {{C_n}{{{h^{m + 1}}} \over {{2^m}}}{f^{(m}}\left( \xi \right)}_{E/{2^m}}$$ $$I + E \approx {I_1} + {I_2} + {E \over {{2^m}}}$$ $${{{2^m} - 1} \over {{2^m}}}E \approx {I_1} + {I_2} - I$$ $$E \approx {{{2^m}} \over {{2^{m}-1}}}\left( {{I_1} + {I_2} - I} \right)$$

Se ha obtenido que si se utiliza la fórmula de Newton-Cotes de orden $n$ para aproximar la función en el intervalo $[a,b]$, tomando $m=n+1$ si n es impar y $m=n+2$ si n es par y considerando las aproximaciones $I$, $I_1$ e $I_2$ respectivamente en los subintervalos $[a,b]$, $[a,\frac{a+b}{2}]$ y $[\frac{a+b}{2},b]$, se cumple que el error $E$ de la aproximación en $[a,b]$ es $$\left| E \right| \approx \left| {{{2^m}} \over {{2^{m}-1}}}\left( {{I_1} + {I_2} - I} \right) \right|$$

Por lo tanto, fijada una precisión $\epsilon$ deseada de la integral, se describe la estrategia para obtener la aproximación con la precisión deseada.

  1. Elegimos una fórmula de Newton-Cotes para aproximar la integral en $[a,b]$.
  2. Subdividimos el intervalo $[a,b]$ en dos subintervalos de la misma longitud y calculamos las aproximaciones de las integrales $I_1$ e $I_2$ en ambos intervalos, con las correspondientes estimaciones de los errores $E_1$ y $E_2$. Definimos los vectores $I=[I_1, \,\,I_2]$ y $E=[E_1, \,\,E_2]$
  3. Si la suma de los errores, sum(E), es inferior a $\epsilon$, tomamos la suma de las aproximaciones $I$ como valor aproximado de la integral y se habrá terminado. Si no es así, $sum(E) \ge \epsilon$, entonces vamos al paso siguiente.
  4. Buscamos el error $E_k$ más grande de los contenidos en el vector $E$. Subdividimos el intervalo asociado a $E_k$ en dos mitades y calculamos las aproximaciones de la integral en cada una de las mitades y los correspondientes errores. Eliminamos $I_k$ y $E_k$ y ponemos en su lugar los dos valores de la integral calculados y los correspondientes errores. Volvemos al paso 3.
Para las práctica utlizaremos los ficheros iehardy.m que a su vez utiliza la función hardy.m, para obtener la aproximación de la integral utilizando la la fórmula de Hardy.
[itg error]=iehardy(a,b,f)
%Devuelve una estimación de la integral y
%el error cometido. Requiere que la
%función f se programe vectorialmente.
Ejemplo: Calcular la integral $\int\limits_0^\pi {{e^{senx\,\cos x}}dx} $ con un error inferior a $\epsilon_a=10^{-12}$ considerando la regla de Hardy.
a=0;b=pi;
format long
f=@(x) exp(sin(x).*cos(x));
error=10^-12;
Dividimos el intervalo en dos partes y aplicamos la fórmula de Newton-Cotes de Hardy. Se tendrá que
x=[a (a+b)/2 b];
[i1 e1]=iehardy(x(1),x(2),f);
[i2 e2]=iehardy(x(2),x(3),f);
E=[e1 e2];I=[i1 i2];
error=sum(E)
itg=sum(I)
Si el error es menor que $\epsilon_a$ habremos terminado y el valor de la integral es itg. Como en este caso no es así, se considera el subintervalo con mayor error. Ejecutando la orden,
[s k]=max(E)
el valor que se obtiene es $k=1$, Se continúa repitiendo el proceso en el intervalo $[x(k),x(k+1)]$ hasta conseguir la precisión considerada.
Los vectores $x$, $E$, $I$ van creciendo según se van tomando subdivisiones en los intervalos.
xn=(x(k)+x(k+1))/2;
x=[x(1:k) xn x(k+1:end)];
[i1 e1]=iehardy(x(k),xn,f);
[i2 e2]=iehardy(xn,x(k+2),f);
E=[E(1:k-1) e1 e2 E(k+1:end)]
I=[I(1:k-1) i1 i2 I(k+1:end)];
itg=sum(I)
error=sum(E)
Se repite el proceso 26 veces obteniendo que el valor de la integral es $ 3.341031544735853$. El valor que devuelve matlab es $3.341031544735852$
integral(f,0,pi)
Si se considera el error absoluto en la precisión de la solución el algoritmo se detiene si $E < \epsilon_a$. Si se usa el error relativo, el algoritmo se detenderá si $E < \epsilon_r|I|$. A menudo se utiliza un test de parada que combina ambos errores: $$E < \epsilon_a+\epsilon_r |I|$$

Usualmente, si la integral es un número grande, el algoritmo se detiene cuando el error relativo es inferior a $\epsilon_r$, mientras que si $|I|$ es pequeño, el algoritmo finaliza cuando el error absoluto es inferior a $\epsilon_a$.

En general, se tendrá que el código Matlab a ejecutar es
%ea error absoluto
%er error relativo
x=[a (a+b)/2 b]
[i1 e1]=iehardy(x(1),x(2),f)
[i2 e2]=iehardy(x(2),x(3),f)
I=[i1 i2];E=[e1 e2];
error=sum(E);
if error<ea
   itg=sum(I);
   [itg error]
else
  [s,k]=max(E)
end
parar=0
while parar==0
  xn=(x(k)+x(k+1))/2
  x=[x(1:k) xn x(k+1:end)]
  [i1 e1]=iehardy(x(k),xn,f);
  [i2 e2]=iehardy(xn,x(k+2),f);
  E=[E(1:k-1) e1 e2 E(k+1:end)];
  I=[I(1:k-1) i1 i2 I(k+1:end)];
  error=sum(E);
  if error < ea+er*abs(itg)
   itg=sum(I);
   [itg error]
   parar=1;
  else
      [s,k]=max(E);
  end
end

Cálculo de Integrales impropias

En este apartado, veremos cómo proceder cuando el intervalo $[a,b]$ no es acotado. En el primer apoartado analizaremos el caso en el que $a$ o $b$ o ambos no son finitos (integrales impropias de primera especie) y en el segundo apartado cuando $f$ tenga una singularidad en un punto $x_o$ en $[a,b]$ de forma que se cumple $\mathop {\lim }\limits_{x \to {x_o}} \left| {f\left( x \right)} \right| = + \infty $ (integrales impropias de segunda especie).

Integrales impropias de primera especie

Consideraremos en este caso integrales del tipo $$\int\limits_a^\infty {f\left( x \right)dx} = \mathop {\lim }\limits_{b \to \infty } \int\limits_a^b {f\left( x \right)dx} $$ donde $f$ es continua. Cuando el límite anterior existe, la integral impropia es convergente. En este caso se tendrá que $$\mathop {\lim }\limits_{b \to \infty } \int\limits_b^\infty {f\left( x \right)dx} = 0$$ En primer lugar se hallará un valor de $b$ de forma que $$\left| {\int\limits_b^\infty {f\left( x \right)dx} } \right| < {\varepsilon \over 2}$$

y luego se buscará una aproximación de la intengral $Itg$ de forma que $$\left| {\int\limits_a^b {f\left( x \right)dx} - Itg} \right| < {\varepsilon \over 2}$$ De forma análoga se podrá calcular las integrales $${\int\limits_{ - \infty }^a {f\left( x \right)dx} }$$

En el caso de una integral de la forma $${\int\limits_{ - \infty }^\infty {f\left( x \right)dx} }$$ se tendrá en cuenta que $$\int\limits_{ - \infty }^\infty {f\left( x \right)dx} = \int\limits_{ - \infty }^0 {f\left( x \right)dx} + \int\limits_0^\infty {f\left( x \right)dx} $$ buscando una aproximación de cada una de ellas con un error menor que $\epsilon/2$. Alternativamente se puede buscar números $a<0$ y $b>0$ de forma que $$\left| {\int\limits_{ - \infty }^a {f\left( x \right)dx} } \right| < {\varepsilon \over 4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| {\int\limits_b^\infty {f\left( x \right)dx} } \right| < {\varepsilon \over 4}\,\,\,\,\,\,\,\,\,\left| {\int\limits_a^b {f\left( x \right)dx} } \right| < {\varepsilon \over 2}$$

Ejercicio Calcular $\int\limits_0^\infty {{e^{ - x}}{{\cos }^2}\left( x \right)dx} $ considerando $ea=10^{-12}$.

Dado que $$\int\limits_0^\infty {{e^{ - x}}{{\cos }^2}\left( x \right)dx} = \underbrace {\int\limits_0^b {{e^{ - x}}{{\cos }^2}\left( x \right)dx} }_{ = {I_1}} + \underbrace {\int\limits_b^\infty {{e^{ - x}}{{\cos }^2}\left( x \right)dx} }_{ = {I_2}}$$ se debe tomar $b$ de forma que $$\left| {{I_2}} \right| \le {{{{10}^{ - 12}}} \over 2}$$ Puede considerarse $${\log \left( {2 \cdot {{10}^{12}}} \right) \le b}$$ Calbulando $I_1$ con un error menor que $10^{-12}/2$, el valor de la integral es $0.599999999999007$.

Ejercicio Calcular $\int\limits_0^\infty {{e^{ - x}}\log \left( {2 + {\rm{sen}}x} \right)dx} $ considerando $e_a=10^{-12}$.

Solución Matlab: 0.798285100587732

Ejercicio Calcular $\int\limits_0^\infty {{e^{ - {x^4}}}dx} $ considerando $e_a=10^{-12}$.

Solución Matlab: 0.906402477053391

Ejercicio Calcular $\int\limits_0^\infty {{{{\rm{sen}}x} \over {1 + {x^3}}}dx} $ considerando $e_a=10^{-12}$.

Solución Matlab: 0.610912718838516

Ejercicio Calcular $\int\limits_0^\infty {{{{e^{ - x}}} \over {1 + {x^4}}}dx} $ considerando $e_a=10^{-12}$.

Solución Matlab: 0.630477834918498

Integrales impropias de segunda especie

En este tipo de integrales la función $f$ es continua en $[a,b]$ salvo en un punto $x_0$ donde $$\mathop {\lim }\limits_{x \to {x_0}} \left| {f\left( x \right)} \right| = + \infty $$

Caso 1 Si el punto $x_0=a$ será $$\int\limits_a^b {f\left( x \right)dx} = \mathop {\lim }\limits_{\delta \searrow 0} \int\limits_{a + \delta }^a {f\left( x \right)dx} $$ Caso 2 Si el punto $x_0=b$ será $$\int\limits_a^b {f\left( x \right)dx} = \mathop {\lim }\limits_{\delta \searrow 0} \int\limits_a^{b - \delta } {f\left( x \right)dx} $$ Caso 3 Si $X_0$ es un punto interior se define esta integral impropia de la forma siguiente: $$\int\limits_a^b {f\left( x \right)dx} = \mathop {\lim }\limits_{\delta \searrow 0} \int\limits_a^{{x_o} - \delta } {f\left( x \right)dx} + \mathop {\lim }\limits_{\delta \searrow 0} \int\limits_a^{{x_o} + \delta } {f\left( x \right)dx} $$

Dependiendo del caso se actúa de la siguiente manera:

Caso 1 Se busca $\delta$ cumpliendo $$\left| {\int\limits_a^{a + \delta } {f\left( x \right)dx} } \right| < {\varepsilon \over 2}$$ y luego una aproximación verificando $$\left| {\int\limits_{a + \delta }^b {f\left( x \right)dx} } \right| < {\varepsilon \over 2}$$ Se procede de forma análoga en el caso 2.

Caso 3 Se busca un valor de $\delta > 0$ verificando $$\left| {\int\limits_{{x_o} - \delta }^{{x_o}} {f\left( x \right)dx} } \right| + \left| {\int\limits_{{x_o}}^{{x_o} + \delta } {f\left( x \right)dx} } \right| < {\varepsilon \over 2}$$ Después se buscan aproximaciones de las integrales cumpliendo $$\left| {\int\limits_a^{{x_o} - \delta } {f\left( x \right)dx} } \right| < {\varepsilon \over 4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| {\int\limits_{{x_o} + \delta }^b {f\left( x \right)dx} } \right| < {\varepsilon \over 4}$$

Ejercicio Calcular $$\int\limits_0^1 {{{\cos \left( x \right)} \over {2\pi \,{\rm{sen}}\left( {\sqrt x } \right)}}dx} $$ considerando $e_a=10^{-12}$.

Solución Matlab: 0.302993744656398

Octave online

Octave es una alternativa a Matlab con un aspecto y unos comandos y sintasis similares. Se trata de un lenguaje interpretado de alto nivel. Lo puedes descargar desde su página oficial completamente gratis. Aquí tienes el enlace de descarga.

Pero además, puedes utilizar una versión en línea desde tu móvil en el caso de que no tengas a mano tu ordenador. Esta versión la tienes aquí: Octave online.