Métodos numéricos
Libro interactivo

Métodos Numéricos

Elena E. Álvarez Saiz

Red Educativa Digital Descartes.
Universidad de Cantabria

Título de la obra:
MÉTODOS NUMÉRICOS


Autores:
Elena E. Alvarez Saiz



Diseño del libro: Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$


Primera Edición



LICENCIA

Creative Commons Attribution License 4.0.

Tabla de contenido

Capítulo III

Aproximación de
funciones de una
variable por polinomios

Introducción

A menudo se dispone de una tabla de datos obtenida por muestreo o experimentación y se supone que los datos corresponden a los valores de una función $f$ desconocida o, aunque sea conocida, se precisa cambiarla por una más sencilla de calcular. Un caso particular de ajuste de curvas consiste en construir un polinomio $P(x)$ que pase por los puntos de esta tabla de valores.

Imaginemos por ejemplo que se tiene una tabla que relaciona la viscosidad dinámica del agua con la temperatura

T ºC 0 5 10 20
$\mu_o$ 1.787 1.519 1.307 1.002

¿Cómo estimar la viscosidad a una temperatura de 7.5º?

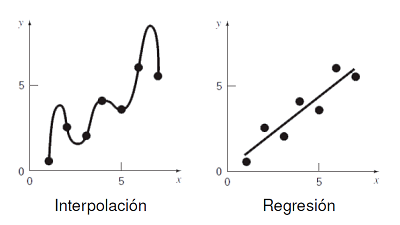
En este capítulo mostraremos dos técnicas para aproximar la función por un polinomio: la interpolación y la aproximación por mínimos cuadrados. Dentro de la interpolación veremos la interpolación de Lagrange y la de Hermite.

Interpolación de Lagrange

DEFINICIÓN. Dados $n+1$ puntos distintos ${x_0,x_1,...,x_n}$ en el intervalo $[a,b]$, el polinomio de Lagrange Joseph Louis Lagrange (1736-1813) fue uno de los más grandes matemáticos de su tiempo. Nació en Italia pero se nacionalizó Francés. Hizo grandes contribuciones en todos los campos de la matemática y también en mecánica. Su obra principal es la “Mécanique analytique”(1788). 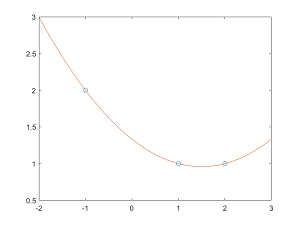En esta obra de cuatro volúmenes, se ofrece el tratamiento más completo de la mecánica clásica desde Newton y sirvió de base para el desarrollo de la física matemática en el siglo XIX. de una función $f$ definida en $[a,b]$ es el polinomio de grado menor o igual a $n$ que cumple $p(x_i)=f(x_i)$ para cada i entre 0 y n. A los puntos ${x_0,x_1,...,x_n}$ se les llama nodos de interpolación.
TEOREMA. El polinomio de interpolación de Lagrange posee una única solución y viene dado mediante la fórmula: $$p\left( x \right) = \sum\limits_{i = 0}^n {f\left( {{x_i}} \right){l_i}\left( x \right)} $$ donde $\left\{ {{l_i}} \right\}_{i = 0}^n$ son los polinomios de base de Lagrange asociados a los nodos $\left\{ {{x_i}} \right\}_{i = 0}^n$ que vienen dados por las expresiones: $${l_i}\left( x \right) = \prod_{ j = 0 \,\,\,\, j \ne i \,\,\,\,}^n {{{x - {x_j}} \over {{x_i} - {x_j}}}} $$

Ejercicio 1 propuesto del tema 3. Calcular los polinomios de base de Lagrange asociados a los nodos $x_0=-1$, $x_1=1$ y $x_2=2$. Calcula el polinomio que interpola en dichos nodos a la función $f$ real en $[-1,2]$ que satisface $f(x_0)=2$, $f(x_1)=1$ y $f(x_2)=1$.

Los datos son: $${x_o} = - 1\,\,\,\,\,\,\,\,\,\,{x_1} = 1\,\,\,\,\,\,\,\,\,\,\,{x_2} = 2$$ $$f\left( {{x_o}} \right) = 2\,\,\,\,\,\,\,\,\,\,f\left( {{x_1}} \right) = 1\,\,\,\,\,\,\,\,\,\,f\left( {{x_2}} \right) = 1$$ Los polinomios base de Lagrange $${l_o}\left( x \right) = {1 \over 6}{x^2} - {1 \over 2}x + {1 \over 3}$$ $${l_1}\left( x \right) = -{1 \over 2}{x^2} + {1 \over 2}x + 1 \,\,\,\,\,{l_2}\left( x \right) = {1 \over 3}{x^2} - {1 \over 3}$$ El polinomio interpolador es: $$p\left( x \right) = f(x_o){l_0}\left( x \right) + f(x_1){l_1}\left( x \right) + f(x_2){l_0}\left( x \right) =$$ $$={1 \over 6}{x^2} - {1 \over 2}x + {4 \over 3}$$ Se puede comprobar que: $$p\left( { - 1} \right) = 2\,\,\,\,\,\,\,\,\,\,p\left( 1 \right) = 1\,\,\,\,\,\,\,\,\,\,p\left( 2 \right) = 1$$

Aunque la fórmula del teorema anterior posee un interés teórico, no es la forma eficiente de calcular el polinomio interpolador. Un método sencillo y más rápido es el siguiente.

Como se quiere calcular $p(x) = {a_o} + {a_1}x + ... + {a_n}{x^n}$ de forma que $p({x_i}) = f\left( {{x_i}} \right)$, se tendrá que cumplir que: $$\begin{pmatrix} {x_{o}^n}&{x_{o}^n}&{...}&{x_0}&1\\ {{x_{1}^n}}&{{x_{1}^n}}&{...}&{x_{1}}&1\\ {...}&{...}&{...}&{...}&{...}\\ {{x_{n-1}^n}}&{{x_{n-1}^n}}&{...}&{x_{n-1}}&1\\ {{x_{n}^n}}&{{x_{n}^n}}&{...}&{x_{n}}&1\\ \end{pmatrix} \begin{pmatrix} {a_n} \\ {a_{n-1}} \\ {...}\\ {a_1}\\ {a_0} \end{pmatrix} = \begin{pmatrix} {f\left( {{x_o}} \right)}\\ {f\left( {{x_1}} \right)}\\ {...}\\ {f\left( {{x_{n-1}}} \right)}\\ {f\left( {{x_n}} \right)} \end{pmatrix}$$

El método consiste en construir la matriz $A$ de orden $(n+1) \times (n+1)$, el vector b de $\mathbb{R}^n$ y resolver el sistema $Aa=b$, donde $a$ es el vector de los coeficientes. Dado que el problema de interpolación de Lagrange tiene una única solución, la matriz $A$ es invertible.

Ejercicio propuesto del tema 3. Calcular el polinomio interpolador de grado 2 de una función que verifica $f(-1)=2$, $f(1)=1$ y $f(2)=1$.

x=[-1 1 2]';b=[2 1 1]';n=2;
A=ones(n+1,1);t=A;
for k=1:n
 t=t.*x;
 A=[t,A];
end
a=A\b
%Comprobación
polyval(a,x)
Ejemplo Interpolar con Matlab $f(x)=e^x$ en el intervalo $[0,1]$ con polinomios de grado 5, 10, 15. Evaluar la función y el polinomio en 500 puntos del intervalo y ver cuál es el máximo de la diferencia entre la función y el polinomio en esos puntos.
COTA DEL ERROR Supongamos que la función $f$ es $n+1$ veces derivable en el intervalo $[a,b]$ y que $f^{(n+1}$ es una función continua. Una cota del error de interpolación de Lagrange viene dado por la expresión $$\left| {f\left( x \right) - p\left( x \right)} \right| \le {{\mathop {\max }\limits_{c \in \left[ {a,b} \right]} \left| {{f^{(n + 1}}\left( c \right)} \right|} \over {\left( {n + 1} \right)!}}\left| {\prod_{j = 0}^n {\left( {x - {x_j}} \right)} } \right|$$

Ejercicio propuesto del tema 3. . Si consideramos una función $f$ en el intervalo $[-1,2]$ cumpliendo $f(-1)=2$, $f(1)=1$ y $f(2)=1$, calcular una cota del error en $[-1,2]$ del polinomio interpolador de Lagrange que aproxima a la función en esos puntos en términos del máximo de $|f^{(n+1}(x)|$ ($n$ es el grado del polinomio, en este caso 2).

Si llamamos M a la cota de la derivada tercera de $f$ en el intervalo, se tendrá que $$\left| {f\left( x \right) - p\left( x \right)} \right| \le {M \over {3!}}\left| {\left( {x - {x_o}} \right)\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)} \right|$$ $$\left| {f\left( x \right) - p\left( x \right)} \right| \le {M \over {3!}}\left| {\left( {x + 1} \right)\left( {x - 1} \right)\left( {x - 2} \right)} \right|$$ Para obtener el máximo de $q(x)=(x+1)(x-1)(x-2)$ se calculan las raíces de $q'(x)$, que serán los puntos donde tiene un máximo o mínimo y se evalúa $q$ en esos valores obteniendo la cota como el valor más grande de todos ellos en valor absoluto.
format long
q=poly([-1 1 2]);dq=polyder(q);
r=roots(dq);v=polyval(q,r)
max(abs(v))
%2.112611790922380
La cota del error es entonces: M*2.112611790922380/6.

La elección de nodos que permite minimizar el valor de \[\mathop {\max }\limits_{x \in \left[ {a,b} \right]} \left| {\prod\limits_{j = 0}^n {\left( {x - {x_j}} \right)} } \right|\] se consigue con los puntos de Chebyshev.

Estos nodos en [0,1] son las raíces del polinomio del $n+1$-ésimo polinomio de Chebyshev que se define de forma recurrente: $${T_o}\left( x \right) = 1\,\,\,\,\,\,\,\,\,\,\,{T_1}(x) = x$$ $${T_k}(x) = 2x{T_{k - 1}}\left( x \right) - {T_{k - 2}}\left( x \right)\,\,\,\,\,\,\,k \ge 2$$ Se puede demostrar que $${T_{n + 1}}(x) = \cos \left( {\left( {n + 1} \right)arc\cos \left( x \right)} \right)\,$$

Nodos de Chebyshev. Los nodos de Chebyschev Pafnuti Lvóvich Tchebyschev (1821 - 1894). El más prominente miembro de la escuela de matemáticas de St. Petersburg. Hizo investigaciones en Mecanismos, Teoría de la Aproximación de Funciones, Teoría de los Números, Teoría de Probabilidades y Teoría de Integración. Sin embargo, escribió acerca de muchos otros temas: formas cuadráticas, construcción de mapas, cálculo geométrico de volúmenes, etc. en $[a,b]$ se calculan como $${x_i} = {{a + b} \over 2} + {{b - a} \over 2}\cos \left( {{{\left( {2i + 1} \right)\pi } \over {2n + 2}}} \right)\,\,\,\,\,\,\,0 \le i \le n$$

Ejemplo. Considerando el intervalo $[-3,3]$ y que $n=8$ es el grado del polinomio de interpolación, calcular los nodos de Chebyshev (9 nodos) y dibujarlos.
n=8;a=-3;b=3;
%Para obtener los nodos en un vector
x=(a+b)/2+(b-a)/2*cos((2*(0:n)+1)*pi/(2*n+2));
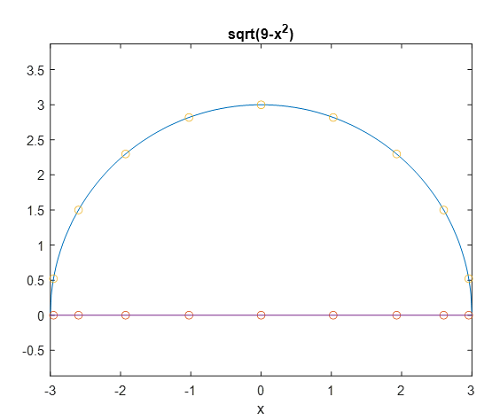
Considerando estos nodos se cumple: $$\max \left| {\prod\limits_{j = 0}^n {\left( {x - {x_j}} \right)} } \right| = {{{{\left( {b - a} \right)}^{n + 1}}} \over {{2^{2n + 1}}}}$$

Ejercicio propuesto del tema 3.

Ejercicio propuesto del tema 3. Interpola la función $f(x)=log(x)$ en los nodos ${0.99, 1, 1.1}$ utilizando polinomios de Lagrange y obtén aproximaciones de $log(x)$ en los puntos $0.95678$ y $1.03597$. Compara los valores obtenidos con los exactos.

Aproxima también $f$ en los mismos puntos mediante el polinomio de grado 2 de Lagrange considerando los nodos de Chebyshev en el intervalo $[0.9,1.1]$.

Interpolación de Hermite

DEFINICIÓN. Sea $f$ una función real definida en el intervalo $[a,b]$, ${x_0,x_1,...,x_k}$ son $k+1$ puntos distintos del intervalo $[a,b]$ y ${\alpha_0,\alpha_1,...,\alpha_k}$ $k+1$ enteros no negativos. El problema de interpolación de Hermite consiste en determinar un polinomio de grado menor o igual que $n=k+\alpha_0+\alpha_1+...+\alpha_k$ satisfaciendo $$p\left( {{x_o}} \right) = f\left( {{x_o}} \right){\mkern 1mu} \,\,\,\,\,p'\left( {{x_o}} \right) = f'\left( {{x_o}} \right)\,\,\,...\,\,\,{p^{({\alpha _o}}}\left( {{x_o}} \right) = \,{f^{({\alpha _o}}}\left( {{x_o}} \right)$$ $$p\left( {{x_1}} \right) = f\left( {{x_1}} \right){\mkern 1mu} \,\,\,\,\,p'\left( {{x_1}} \right) = f'\left( {{x_1}} \right)\,\,\,...\,\,\,{p^{({\alpha _1}}}\left( {{x_1}} \right) = \,{f^{({\alpha _1}}}\left( {{x_1}} \right)$$ $$...$$ $$p\left( {{x_k}} \right) = f\left( {{x_k}} \right){\mkern 1mu} \,\,\,\,\,p'\left( {{x_k}} \right) = f'\left( {{x_k}} \right)\,\,\,...\,\,\,{p^{({\alpha _k}}}\left( {{x_k}} \right) = \,{f^{({\alpha _k}}}\left( {{x_k}} \right)$$ Nota: En el caso particular en que $\alpha_i=1$ para cada $i$, entonces el problema se denomina interpolación de Hermite clásica.
Es importante que en cada nodo $x_i$ que se imponga una condición sobre la derivada de orden $\alpha_i$, se imponga tambien una condición sobre cada derivada inferior a $\alpha_i$ y la valor de la función. En otro caso, los problemas seríann de interpolación de Birkhoff que no tienen solución en todos los casos.
TEOREMA. El problema de interpolación de Hermite posee una única solución.
COTA DEL ERROR. Supongamos que la función $f$ es $n+1$ veces derivable en el intervalo $[a,b]$ y que $f^{n+1}$ derivable en el intervalo $[a,b]$ y que $f^{(n+1}$ es una función continua, entonces una cota del error de interpolación de Hermite viene dada por la expresión: $$\left| {f\left( x \right) - p\left( x \right)} \right| \le {{\mathop {\max }\limits_{c \in \left[ {a,b} \right]} \left| {{f^{(n + 1}}\left( c \right)} \right|} \over {\left( {n + 1} \right)!}}\left| {\prod\limits_{j = 0}^{} {{{\left( {x - {x_j}} \right)}^{{\alpha _j} + 1}}} } \right|$$

Ejercicios de examen del 6 de febrero del 2014 y del 9 de diciembre de 2014.

Mínimos cuadrados

En el caso de los métodos de interpolación, no siempre se consigue una mejor aproximación aumentado el número de puntos de interpolación (ver por ejemplo la función de Runge).

Además, cuando se considera un número grande de nodos la manipulación y evaluación el cálculo resulta muy costoso computacionalmente y puede llevar también problemas de redondeo importantes.

Con el siguiente método veremos que en el caso de que se tenga mucha información sobre la función en ciertos puntos, en lugar de aumentar de forma considerablemente el grado del polinomio en los métodos de interpolación, es más ventajoso utilizar el método de mínimos cuadrados.

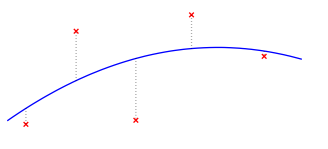
La idea consiste en encontar un polinomio de grado $k$ a partir de un conjunto de $m$ puntos de forma que el polinomio tenga grado inferior al que se podría obtener pasando por todos ellos y se minimice el error que existe entre el valor del polinomio y las ordenadas de los puntos.

En la siguiente herramienta interactiva se realiza el ajuste a una recta.

Se escribe a continuación la formulación del método de mínimos cuadrados.

DEFINICIÓN. Dados $n+1$ puntos distintos ${x_0,x_1,...,x_n}$ en el intervalo $[a,b]$, $n+1$ números reales positivos $\left\{ {{\omega _0},{\omega _1},...,{\omega _n}} \right\}$, $f$ una función definida en $[a,b]$ y un entero $1 \le k \le n$, el problema de mínimos cuadrados consiste en resolver $$\mathop {{(P) \,\,\, \, \rm{minimizar}}}\limits_{p \in {P_k}} \sum\limits_{j = 0}^n {{\omega _j}{{\left( {p\left( {{x_j}} \right) - f\left( {{x_j}} \right)} \right)}^2}} $$ donde $P_k$ denota el espacio de los polinomios de grado menor o igual $k$.
La razón de incluir pesos se justifica, por ejemplo, para ajustar el polinomio a los valores más precisos de $f$ o para obtener más precisión en unas zonas que en otras de un intervalo.

Formulación algebraica del problema

El problema que tratamos de resolver es encontrar el polinomio $p$ de grado menor o igual a $k$ que minimiza la siguiente expresión $$\sum\limits_{j = 0}^n {{\omega _j}} {\left( {p\left( {{x_j}} \right) - f\left( {{x_j}} \right)} \right)^2}$$

Para ver cómo se puede formular algebraicamente este problema, consideremos un polinomio $p$ de grado $k$

$$p\left( x \right) = {a_o} + {a_1}x + {a_2}{x^2} + .. + {a_k}{x^k}$$

y las siguientes matrices

$$A = \begin{pmatrix} {\sqrt {{\omega _0}} \,x_0^k} & {\sqrt {{\omega _0}} \,x_0^{k - 1}} & {...} & {\sqrt {{\omega _0}} \,{x_0}}& {\sqrt {{\omega _0}} }\\ {\sqrt {{\omega _1}} \,x_1^k} & {\sqrt {{\omega _1}} \,x_1^{k - 1}} & {...} & {\sqrt {{\omega _1}} \,{x_1}}& {\sqrt {{\omega _1}} } \\ \vdots & \vdots & {...} & \vdots & \vdots \\ {\sqrt {{\omega _n}} \,x_n^k} & {\sqrt {{\omega _n}} \,x_n^{k - 1}} & {...} & {\sqrt {{\omega _n}} \,{x_n}}& {\sqrt {{\omega _n}} } \\ \end{pmatrix} $$ $$a = \begin{pmatrix} {{a_k}} \\ {{a_{k-1}}} \\ {{a_{k-2}}} \\ \vdots \\ {{a_0}} \\ \end{pmatrix} \,\,\,\,\,\,\,b = \begin{pmatrix} {\sqrt {{\omega _o}} \,f\left( {{x_o}} \right)} \\ {\sqrt {{\omega _1}} \,f\left( {{x_1}} \right)} \\ \vdots \cr {\sqrt {{\omega _n}} \,f\left( {{x_n}} \right)} \\ \end{pmatrix}$$ Se cumple que $$Aa - b = \begin{pmatrix} {\sqrt {{\omega _o}} \left( {p\left( {{x_o}} \right) - f\left( {{x_o}} \right)} \right)} \\ {\sqrt {{\omega _1}} \left( {p\left( {{x_1}} \right) - f\left( {{x_1}} \right)} \right)} \\ \vdots \cr {\sqrt {{\omega _n}} \left( {p\left( {{x_n}} \right) - f\left( {{x_n}} \right)} \right)} \\ \end{pmatrix}$$

Teniendo en cuenta la norma euclidea $${\left\| {Aa - b} \right\|^2} = \sum\limits_{j = 0}^n {{\omega _j}} {\left( {p\left( {{x_j}} \right) - f\left( {{x_j}} \right)} \right)^2}$$ los coeficientes del polinomio $p$ que se busca serían la solución del problema: $$\mathop { (P2) \,\,\,\,{\rm{minimizar}}}\limits_{x \in {{\mathbb R}^{k + 1}}} {\left\| {Ax - b} \right\|^2}$$

Ejemplo: Ajustar un polinomio de grado 2 de la forma $y=a_o+a_1x+a_2x^2$ a un conjunto de observaciones: $(x_0,y_0)$, ($x_1,y_1)$,...,$(x_n,y_n)$ con $n \gt 2$ de manera que se minimice el "residuo", $$\sum\limits_{i = 0}^n {{{\left( {{y_i} - \left( {{a_o} + {a_1}{x_i}+{a_2}{x_i^2}} \right)} \right)}^2}} $$ Es decir, considerando $$A = \begin{pmatrix} {{x_0^2}} &{{x_0}} & 1 \\ {{x_1^2}} &{{x_1}} & 1 \\ {{...}} & {{...}}& {{...}}\\ {{x_n^2}}&{{x_n}} & 1 \\ \end{pmatrix} \,\,\, x = \begin{pmatrix} {{a_2}} \\ {{a_1}} \\ {{a_0}} \\ \end{pmatrix} \,\,\,\, b= \begin{pmatrix} {{y_0}} \\ {{y_1}} \\ {{...}} \\ {{y_n}} \\ \end{pmatrix}$$ se busca el vector $x$ de ${\mathbb R}^3$ solución del problema $$\min \left\| r \right\| = \min \left\| {Ax - b} \right\|$$

Ejemplo: Imaginemos un muelle colgado verticalmente dentro de un cilindro abierto por los extremos a altura 0, por encima de la apertura superior. La longitud del muelle es desconocida porque su extremo inferior está centro del cilindro y es inalcanzable.
$h$ 6 7 10
$F$ 3 8 12

Se desea determinar L, y de paso la constante del muelle usando la ley de Hooke: $F=k(h-L)=kh-kL$ donde $F$ denota la fuerza aplicada al muelle y $h$ es la distancia desde el extremo superior del muelle. Se disponen de los siguientes datos

Llamamos $a_1=k$ y $a_2=-kL$. El sistema resultante de escribir la ley de Hooke es $$ 6{a_1} + {a_2} = 3 $$ $$ 7{a_1} + {a_2} = 8 $$ $$ 10{a_1} + {a_2} = 12 $$ En forma matricial, $Ax=b$ siendo $$ A= \begin{pmatrix} 6&1 \\ 7&1 \\ 10&1 \\ \end{pmatrix} \,\,\,\,\, x= \begin{pmatrix} a_1 \\ a_2\\ \end{pmatrix}\,\,\,\,\, b= \begin{pmatrix} 3 \\ 8\\ 12\\ \end{pmatrix}$$

El problema de mínimos cuadrados consiste en encontrar el vector $x$ de ${\mathbb R}^2$ de forma que sea mínima $\left\| {Ax - b} \right\|$.

Veremos que para resolver el problema en general utilizamos la descomposición QR de la matriz $A$.

Resolución del problema $(P2)$ mediante la factorización QR

El método que se propone es el siguiente

  1. Realizamos la factorización QR de A donde Q es ortogonal, es decir, ${Q^T}Q = Q{Q^T} = I$ y tiene dimensiones $(n+1)\text{x}(n+1)$ y R es una matriz triangular superior $(n+1)\text{x}(k+1)$
  2. Consideramos en Q y R las siguientes submatrices:
    • Q=[Y Z] con Y matriz $(n+1)\text{x}(k+1)$ y Z matriz $(n+1)\text{x}(n-k)$
    • $R = \begin{pmatrix} {\widehat R} \\ 0 \\ \end{pmatrix}$ siendo ${\widehat R}$ es una matriz triangular superior$(k+1)\text{x}(k+1)$ y O es una matriz formada por ceros de orden $(n-k)\text{x} (k+1)$
  3. Los coeficientes del polinomio solución $$a = {\left( {{a_0},{a_1},...,{a_k}} \right)^T}$$ se obtienen resolviendo el sistema de ecuaciones lineales $$\widehat Rx = {Y^T}b$$ y el resiuales $${\mathop{\rm Re}\nolimits} s = \left\| {{Z^T}b} \right\|$$

Veamos la justificación del punto 3. Como Q es ortogonal se cumple $${\left\| {Qv} \right\|^2} = {\left( {Qv} \right)^T}\left( {Qv} \right) = {v^T}\left( {{Q^T}Q} \right)v = {v^T}Iv = {v^T}v = {\left\| v \right\|^2}$$

Por lo tanto, $${\left\| {Ax - b} \right\|^2} = {\left\| {QRx - b} \right\|^2} = {\left\| {Q\left( {Rx - {Q^T}b} \right)} \right\|^2} = $$ $${\left\| {Rx - {Q^T}b} \right\|^2} = {\left\| {\,\left( {_O^{\widehat R}} \right)x - \left( {_{{Z^T}}^{{Y^T}}} \right)b\,} \right\|^2} = {\left\| {\,\left( {_{ - {Z^T}b}^{\widehat Rx - {Y^T}b}} \right)\,} \right\|^2} = $$ $${\left\| {\,\widehat Rx - {Y^T}b\,} \right\|^2} + {\left\| {\,{Z^T}b\,} \right\|^2}$$

El mínimo valor del problema $(P_2)$ se obtiene para el valor de $x$ que hace cero el término $${\left\| {\,\widehat Rx - {Y^T}b\,} \right\|^2}$$.

De la expresión anterior se deduce que, equivalentemente, la solución del problema $(P_2)$ se obtiene calculando el valor $x$ solución del sistema $${\widehat Rx = {Y^T}b}$$

Si $k$ es el grado del polinomio buscado y $QR$ es la factorización de $A$, la matriz $\widehat R$ es la submatriz de $R$ con las primeras $k+1$ filas y la matriz $Y$ es la submatriz de $Q$ considerando las primeras $k+1$ columnas.
Hay que hacer notar que la matriz ${\widehat R}$ es inversible debido a que los nodos $\left\{ {{x_j}} \right\}_{j = 0}^n$ son todos distintos. Por lo tanto, la solución del problema de mínimos cuadrados (Q) existe y es única.
Ejemplo: Considerando el ejemplo anterior de la ley de Hooke, se seguirá el método visto para considerar la recta que resuelve el problema de mínimos cuadrados con los siguientes datos
$h$ 6 7 10
$F$ 3 8 12
En este caso, $$ A= \begin{pmatrix} 6&1 \\ 7&1 \\ 10&1 \\ \end{pmatrix} \,\,\,\,\, x= \begin{pmatrix} a_1 \\ a_2\\ \end{pmatrix}\,\,\,\,\, b= \begin{pmatrix} 3 \\ 8\\ 12\\ \end{pmatrix}$$ La descomposición $QR$ de la matriz $A$ se obtiene con Matlab de la forma
[Q,R]=qr([6 1;7 1;10 1])
$$ Q= \begin{pmatrix} -0.4411 & -0.6777 & -0.5883\\ -0.5147 & -0.3460 & 0.7845\\ -0.7352 & 0.6488 & -0.1961\\ \end{pmatrix} $$
$$ R= \begin{pmatrix} -13.6015 & -1.6910\\ 0 & -0.3749\\ 0 & 0 \\ \end{pmatrix}$$ Como $k$ es 1 al ser una recta, las matrices $Y$, $\widehat R$ son $$ Y= \begin{pmatrix} -0.4411 & -0.6777 \\ -0.5147 & -0.3460 \\ -0.7352 & 0.6488 \\ \end{pmatrix} \,\,\,\,\, \widehat R= \begin{pmatrix} -13.6015 & -1.6910\\ 0 & -0.3749\\ \end{pmatrix}$$ y el sistema a resolver es entonces, $\widehat Rx=Y^Tb$, es decir, $$ \begin{pmatrix} -13.6015 & -1.6910\\ 0 & -0.3749\\ \end{pmatrix} \begin{pmatrix} a_1\\ a_0\\ \end{pmatrix} $$ $$ \,\,\,\,\, = \begin{pmatrix} -0.4411 & -0.5147 & -0.7352 \\ -0.6777 & -0.3460 &0.6488 \\ \end{pmatrix} \begin{pmatrix} 3\\ 8\\ 12\\ \end{pmatrix}$$ es decir, $$ \begin{pmatrix} -13.6015 & -1.6910\\ 0 & -0.3749\\ \end{pmatrix} \begin{pmatrix} a_1\\ a_0\\ \end{pmatrix}=\begin{pmatrix} -14.2632\\ 2.9847\\ \end{pmatrix} $$ La solución de este sistema es $a_1=2.0385$ y $a_o=-7.9615$

Ejercicio 11 propuesto del tema 3.

Octave online

Octave es una alternativa a Matlab con un aspecto y unos comandos y sintasis similares. Se trata de un lenguaje interpretado de alto nivel. Lo puedes descargar desde su página oficial completamente gratis. Aquí tienes el enlace de descarga.

Pero además, puedes utilizar una versión en línea desde tu móvil en el caso de que no tengas a mano tu ordenador. Esta versión la tienes aquí: Octave online.